1.4 角平分线 培优练习(含解析)
图片预览

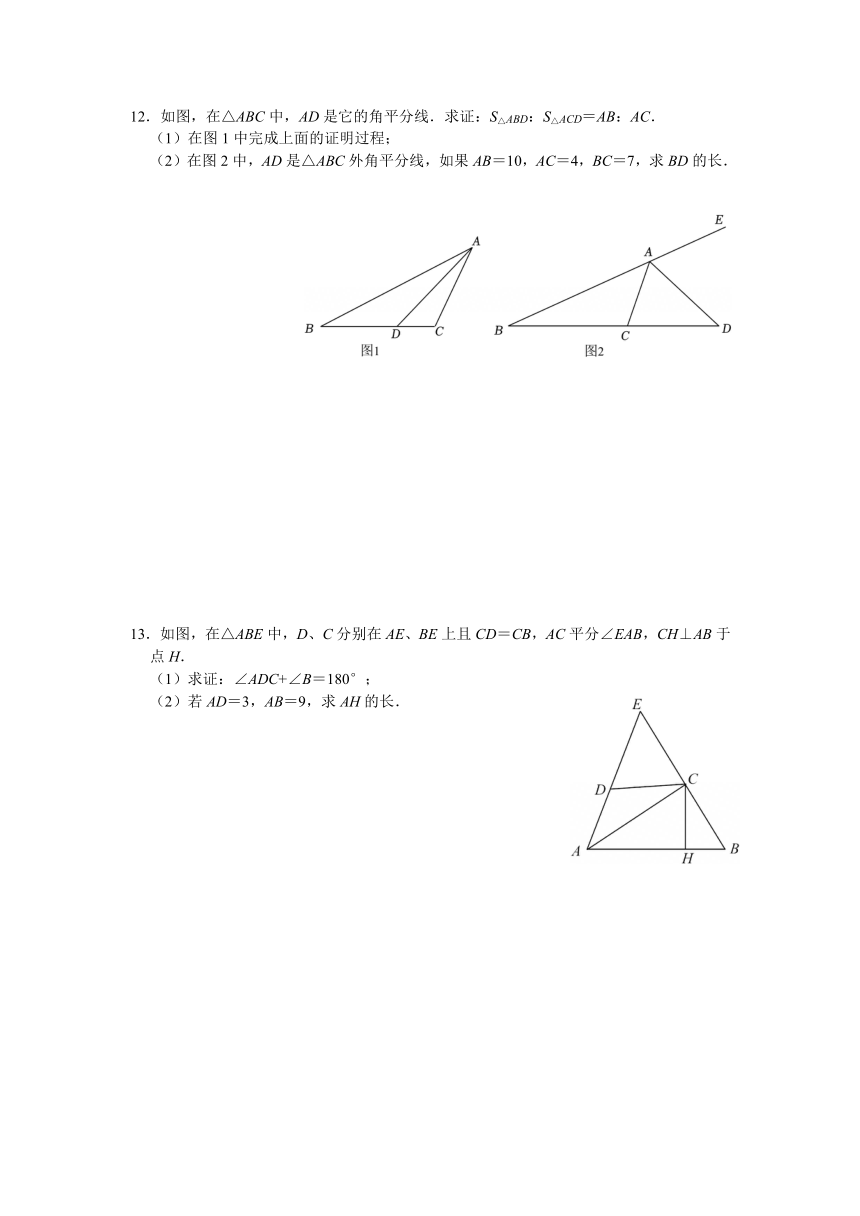
文档简介
1.4角平分线培优练习北师大版2024—2025学年八年级下册
一、选择题
1.如图,直线l1,l2,l3表示三条公路.现要建造一个中转站P,使P到三条公路的距离都相等,则中转站P可选择的点有( )
A.一处 B.二处 C.三处 D.四处
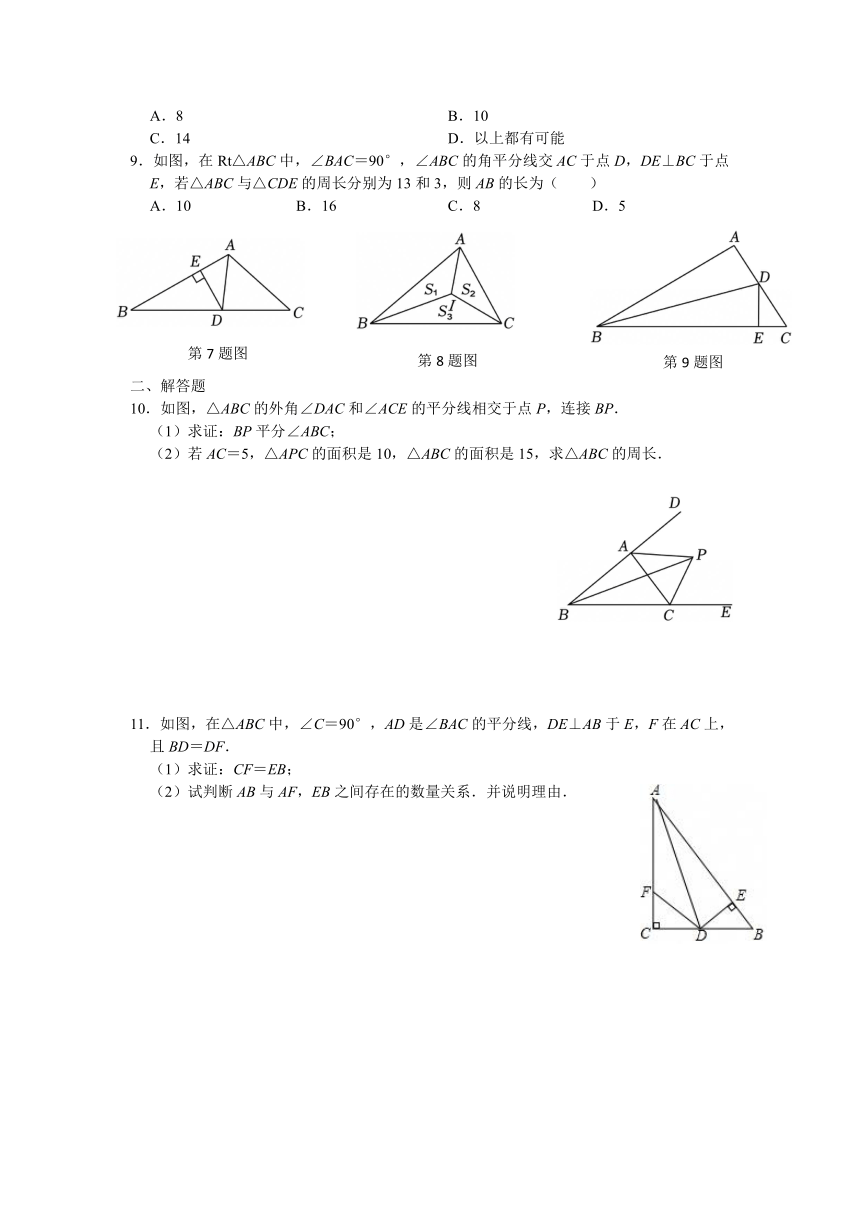
2.如图,在△ABC中,AD是它的角平分线,AB=12cm,AC=9cm,BC=10cm,则S△ABD:S△ACD=( )
A.3:4 B.4:3 C.6:5 D.10:9
3.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=6,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
4.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=10,则点P到BC的距离是( )
A.10 B.8 C.6 D.5
5.如图,OP平分∠AOB,PF⊥OA于点F,点D在OB上,DH⊥OP于点H,若OD=4,OP=8,PF=3.5,则DH的长为( )
A.4.5 B.5 C.7 D.
6.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.6 D.5
8.如图,点I是△ABC三条角平分线的交点,△ABI的面积记为S1,△ACI的面积记为S2,△BCI的面积记为S3,且S3=10,关于S1+S2的值可能为( )
A.8 B.10
C.14 D.以上都有可能
9.如图,在Rt△ABC中,∠BAC=90°,∠ABC的角平分线交AC于点D,DE⊥BC于点E,若△ABC与△CDE的周长分别为13和3,则AB的长为( )
A.10 B.16 C.8 D.5
二、解答题
10.如图,△ABC的外角∠DAC和∠ACE的平分线相交于点P,连接BP.
(1)求证:BP平分∠ABC;
(2)若AC=5,△APC的面积是10,△ABC的面积是15,求△ABC的周长.
11.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
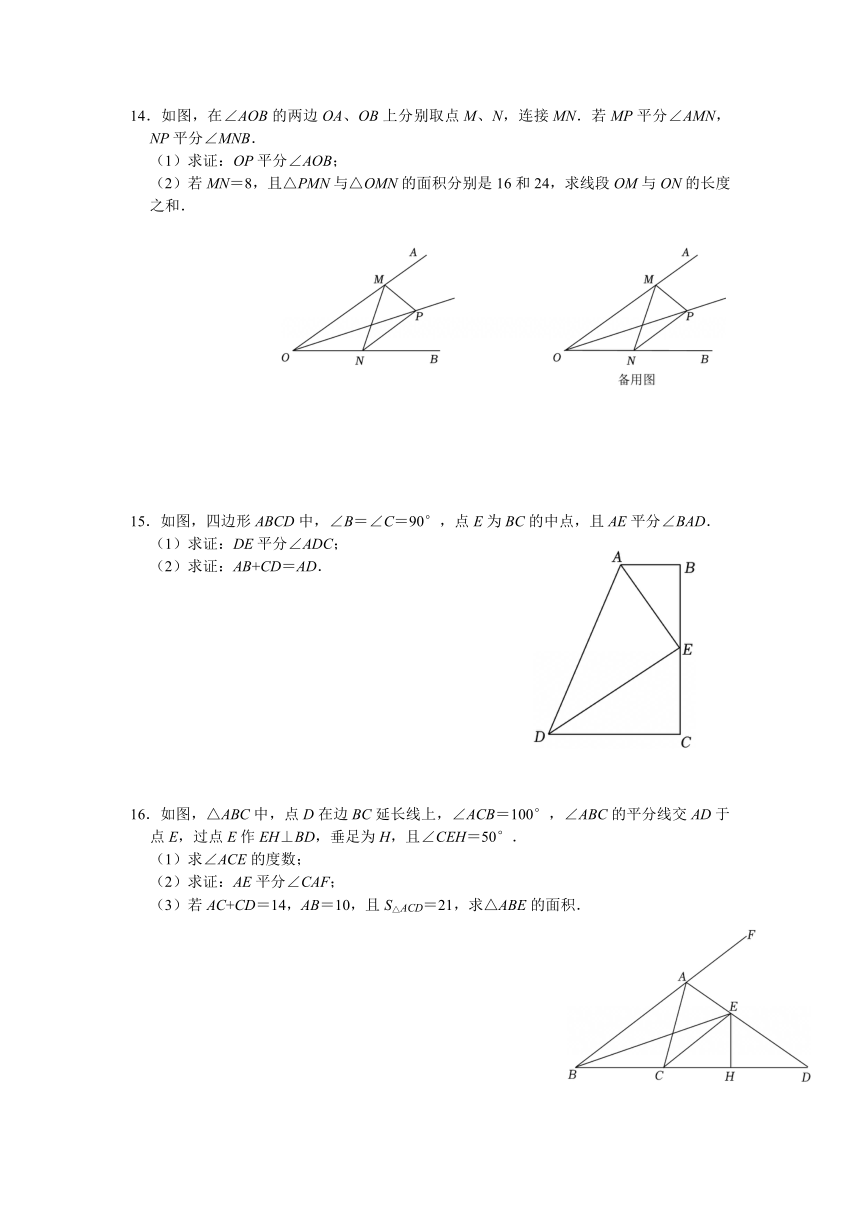
12.如图,在△ABC中,AD是它的角平分线.求证:S△ABD:S△ACD=AB:AC.
(1)在图1中完成上面的证明过程;
(2)在图2中,AD是△ABC外角平分线,如果AB=10,AC=4,BC=7,求BD的长.
13.如图,在△ABE中,D、C分别在AE、BE上且CD=CB,AC平分∠EAB,CH⊥AB于点H.
(1)求证:∠ADC+∠B=180°;
(2)若AD=3,AB=9,求AH的长.
14.如图,在∠AOB的两边OA、OB上分别取点M、N,连接MN.若MP平分∠AMN,NP平分∠MNB.
(1)求证:OP平分∠AOB;
(2)若MN=8,且△PMN与△OMN的面积分别是16和24,求线段OM与ON的长度之和.
15.如图,四边形ABCD中,∠B=∠C=90°,点E为BC的中点,且AE平分∠BAD.
(1)求证:DE平分∠ADC;
(2)求证:AB+CD=AD.
16.如图,△ABC中,点D在边BC延长线上,∠ACB=100°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=50°.
(1)求∠ACE的度数;
(2)求证:AE平分∠CAF;
(3)若AC+CD=14,AB=10,且S△ACD=21,求△ABE的面积.
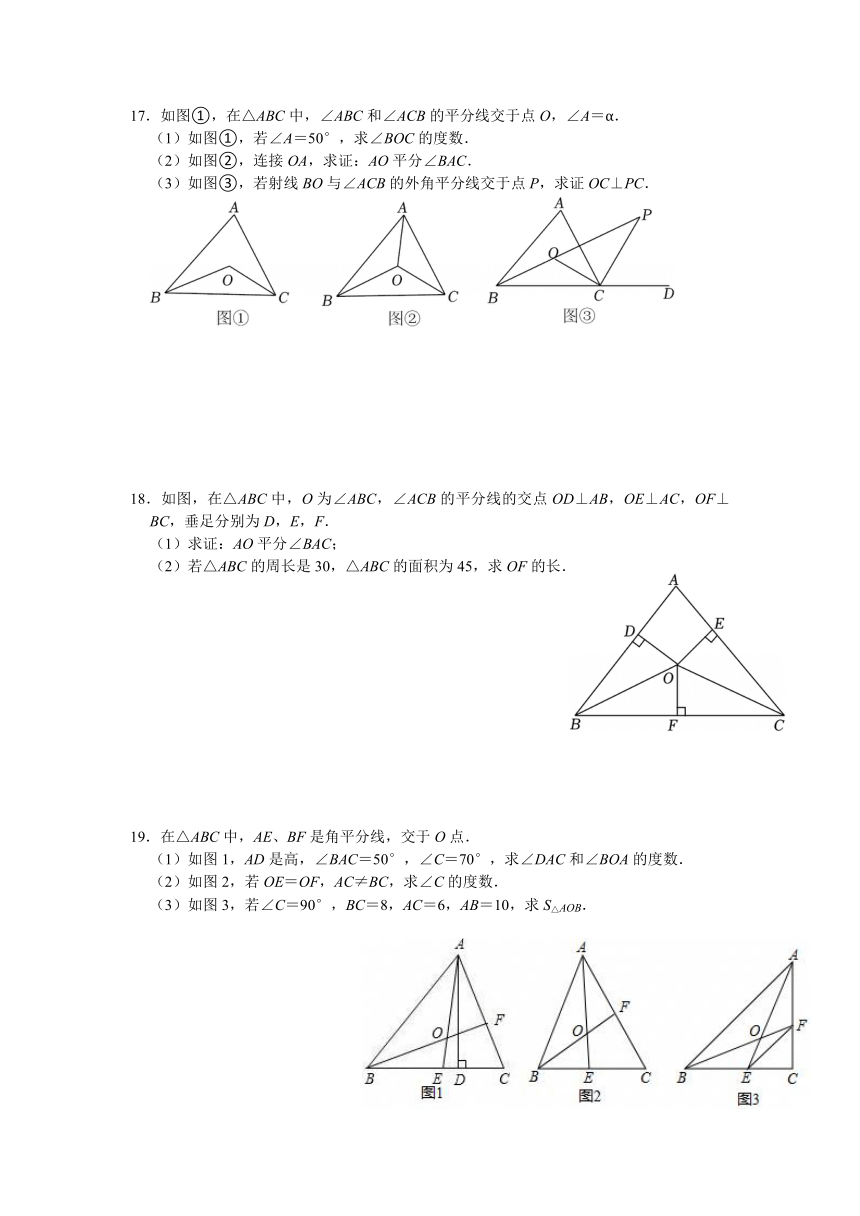
17.如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.
(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:AO平分∠BAC.
(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
18.如图,在△ABC中,O为∠ABC,∠ACB的平分线的交点OD⊥AB,OE⊥AC,OF⊥BC,垂足分别为D,E,F.
(1)求证:AO平分∠BAC;
(2)若△ABC的周长是30,△ABC的面积为45,求OF的长.
19.在△ABC中,AE、BF是角平分线,交于O点.
(1)如图1,AD是高,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的度数.
(2)如图2,若OE=OF,AC≠BC,求∠C的度数.
(3)如图3,若∠C=90°,BC=8,AC=6,AB=10,求S△AOB.
参考答案
1.【解答】解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三个外角两两平分线的交点,共三处.
故选:D.
2.【解答】解:设△ABD的边AB上的高与△ACD的AC上的高分别为h1,h2,
∵在△ABC中,AD是它的角平分线,
∴h1=h2,
∴△ABD与△ACD的面积之比
=4:3.
故选:B.
3.【解答】解:作DE⊥AB于点E,
,
由题意可知,AD是∠CAB的平分线,
∵∠C=90°,
∴DC⊥AC,
∵DE⊥AB,CD=6,
∴DE=CD=6,
∵AB=15,
∴,
故选:C.
4.【解答】解:过点P作PE⊥BC于E,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,
∵BP和CP分别平分∠ABC和∠DCB,AD⊥AB,AD⊥CD,PE⊥BC,
∴PA=PE=PD,
∵AD=10,
∴PE=5,即点P到BC的距离是5,
故选:D.
5.【解答】解:作PN⊥OB于N,
∵OP平分∠AOB,PF⊥OA,PN⊥OB,
∴PF=PN=3.5,
∵S△ODPOP×DHOD×PN,
∴8×DH4×3.5,
解得,DH,
故选:D.
6.【解答】解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵点O是内心,
∴OE=OF=OD,
∴S△ABO:S△BCO:S△CAO AB OE: BC OF: AC OD=AB:BC:AC=2:3:4,
故选:C.
7.【解答】解:过点D作DF⊥AC于F,
∵AD是的角平分线,DE⊥AB,
∴DE=DF=2,
∴S△ABC=S△ABD+S△ADCAB DEAC DF4×2AC×2=7,
解得AC=3.
故选:A.
8.【解答】解:∵点I是△ABC三条角平分线的交点,
∴△ABI、△ACI和△BCI的边AB、AC和BC边上的高相等,
设△ABI、△ACI和△BCI的高为h,
∴,,
由三角形三边关系得AB+AC>BC,
∴S1+S2>S3,
又∵S3=10,
∴S1+S2>10,故S1+S2的值可能为14,选项C符合题意,
选项A、B、D不符合题意.
故选:C.
9.【解答】解:∵∠BAC=90°,BD平分∠ABC,DE⊥BC,
∴AD=DE,
在Rt△ABD和Rt△EBD中,
,
∴Rt△ABD≌Rt△EBD(HL),
∴AB=BE,
∵△ABC与△CDE的周长分别为13和3,
∴AB+BC+AC=AB+AC+BE+EC=13,DE+EC+DC=AD+EC+DC=AC+EC=3,
∴AB+BE=10,
∴AB=BE=5.
故选:D.
10.【解答】(1)证明:如图,过点P作PF⊥BD于F,PG⊥AC于G,PH⊥BE于H,
∵AP平分∠DAC,PF⊥BD,PG⊥AC,
∴PF=PG,
∵CP平分∠ACE,PH⊥BE,PG⊥AC,
∴PH=PG,
∴PF=PH,
∵PF⊥BD,PH⊥BE,
∴BP平分∠ABC;
(2)∵AC=5,△APC的面积是10,
∴5×PG=10,
∴PG=4,
∴PF=PH=PG=4,
∵△ABC的面积是15,△APC的面积是10,
∴AB×PFBC×PH=25,
∴AB+BC=12.5,
∴△ABC的周长=AB+BC+AC=12.5+5=17.5.
11.【解答】(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△FCD和Rt△BED中,
,
∴Rt△FCD≌Rt△BED(HL),
∴CF=EB;
(2)解:AB=AF+2BE,
理由如下:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴AB=AE+BE=AF+FC+BE=AF+2BE.
12.【解答】(1)证明:如图1中,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠ABC,
∴DE=DF,
∴;
(2)解:如图2中,过点D作DM⊥AE于点M,DN⊥AC于点N.
∵AD平分∠EAC,
∴DM=DN,
∴,
∴,
∴,
∴CD,
∴BD=BC+CD=7.
13.【解答】(1)证明:过点C作CM⊥DE,垂足为M,
∵AC平分∠EAB,CH⊥AB,CM⊥DE,
∴CM=CH,∠CMA=∠CHB=90°,
在Rt△DMC与Rt△BHC中
,
∴Rt△DMC≌Rt△BHC(HL),
∴DM=BH,∠1=∠B,
∵∠1+∠CDA=180°,
∴∠ADC+∠B=180°;
(2)解:∵∠CMA=∠CHB=90°,
在Rt△AMC与Rt△AHC中
,
∴Rt△AMC≌Rt△AHC(HL),
∴AM=AH,
设BH=DM=x,
则AH=9﹣x,AM=3+x,
∴9﹣x=3+x,
解得x=3,
∴AH=6.
14.【解答】(1)证明:过点P作PC⊥OA,垂足为C,过点P作PD⊥MN,垂足为D,过点P作PE⊥OB,垂足为E,
∵MP平分∠AMN,PC⊥OA,PD⊥MN,
∴PC=PD,
∵NP平分∠MNB,PD⊥MN,PE⊥OB,
∴PD=PE,
∴PC=PE,
∴OP平分∠AOB;
(2)∵△PMN的面积是16,MN=8,
∴MN PD=16,
∴8 PD=16,
∴PD=4,
∴PD=PC=PE=4,
∵△OMN的面积是24,
∴四边形MONP的面积=△PMN的面积+△OMN的面积=16+24=40,
∴△POM的面积+△PON的面积=40,
∴OM PCON PE=40,
∴OM 4ON 4=40,
∴OM+ON=20,
∴线段OM与ON的长度之和为20.
15.【解答】证明:(1)如图,过点E作EF⊥AD于F,
∵∠B=90°,AE平分∠DAB,
∴BE=EF,
∵E是BC的中点,
∴BE=CE,
∴CE=EF,
又∵∠C=90°,EF⊥AD,
∴DE是∠ADC的平分线.
(2)∵AE平分∠BAD,DE平分∠ADC,EF⊥AD,∠B=∠C=90°,
∴AB=AF,DC=DF,
∴AB+CD=AF+FD=AD.
16.【解答】解:(1)∵∠ACB=100°,
∴∠ACD=180°﹣100°=80°,
∵EH⊥BD,
∴∠CHE=90°,
∵∠CEH=50°,
∴∠ECH=90°﹣50°=40°,
∴∠ACE=∠ACD﹣∠ECH=80°﹣40°=40°.
(2)证明:如图:过E点分别作EM⊥BF于M,EN⊥AC与N,
∵BE平分∠ABC,
∴EM=EH,
∵∠ACE=∠ECH=40°,
∴CE平分∠ACD,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF.
(3)解:∵AC+CD=14,S△ACD=21,EM=EN=EH,
∴,
即,解得EM=3,
∵AB=10,
∴.
17.【解答】(1)解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=130°,
∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB∠ABC∠ACB=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°;
(2)证明:过点O作OD⊥BC,OE⊥AB,OF⊥AC,垂足分别为D,E,F,
∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,
∴OD=OE,OD=OF,
∴OE=OF,
∴OA平分∠BAC;
(3)证明:∵OC平分∠ACB,CP平分∠ACD,
∴∠ACO∠ACB,∠ACP∠ACD,
∴∠OCP=∠ACO+∠ACP
∠ACB∠ACD
∠BCD
180°
=90°,
∴OC⊥CP.
18.【解答】(1)证明:如图,连接OA,
∵OB为∠ABC的平分线,OD⊥AB,OF⊥BC,
∴OD=OF,
∵OC为∠ACB的平分线的交点OE⊥AC,OF⊥BC,
∴OE=OF,
∴OD=OE=OF
在Rt△AOD与Rt△AOE中,,
∴Rt△AOD≌Rt△AOE(HL)
∴∠OAD=∠OAE,
∴AO平分∠BAC.
(2)解:由(1)知OD=OE=OF,
∴S△AOB+S△BOC+S△AOC,
∵S△ABC=45,AB+BC+AC=30,
∴,
∴OF=3.
19.【解答】解:(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°﹣90°﹣70°=20°;
∵∠BAC=50°,∠C=70°,
∴∠BAO=25°,∠ABC=60°,
∵BF是∠ABC的角平分线,
∴∠ABO=30°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°;
(2)连接OC,
∵AE、BF是角平分线,交于O点,
∴OC是∠ACB的角平分线,
∴∠OCF=∠OCE,
过O作OM⊥BC,ON⊥AC,
则OM=ON,
在Rt△OEM与Rt△OFN中,,
∴Rt△OEM≌Rt△OFN,(HL),
∴∠EOM=∠FON,
∴∠MON=∠EOF=180°﹣∠ACB,
∵AE、BF是角平分线,
∴∠AOB=90°∠ACB,
即90°∠ACB=180°﹣∠ACB,
∴∠ACB=60°;
(3)连接OC,过O作OD⊥AB于D,OG⊥BC于G,OH⊥AC于H,
∵AE、BF是角平分线,交于O点,
∴OD=OG=OH,
∴S△ABC8×610OD6×OG8×OH,
∴OD=2,
∴S△AOB10×2=10.
一、选择题
1.如图,直线l1,l2,l3表示三条公路.现要建造一个中转站P,使P到三条公路的距离都相等,则中转站P可选择的点有( )
A.一处 B.二处 C.三处 D.四处
2.如图,在△ABC中,AD是它的角平分线,AB=12cm,AC=9cm,BC=10cm,则S△ABD:S△ACD=( )
A.3:4 B.4:3 C.6:5 D.10:9
3.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=6,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
4.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=10,则点P到BC的距离是( )
A.10 B.8 C.6 D.5
5.如图,OP平分∠AOB,PF⊥OA于点F,点D在OB上,DH⊥OP于点H,若OD=4,OP=8,PF=3.5,则DH的长为( )
A.4.5 B.5 C.7 D.
6.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.6 D.5
8.如图,点I是△ABC三条角平分线的交点,△ABI的面积记为S1,△ACI的面积记为S2,△BCI的面积记为S3,且S3=10,关于S1+S2的值可能为( )
A.8 B.10
C.14 D.以上都有可能
9.如图,在Rt△ABC中,∠BAC=90°,∠ABC的角平分线交AC于点D,DE⊥BC于点E,若△ABC与△CDE的周长分别为13和3,则AB的长为( )
A.10 B.16 C.8 D.5
二、解答题
10.如图,△ABC的外角∠DAC和∠ACE的平分线相交于点P,连接BP.
(1)求证:BP平分∠ABC;
(2)若AC=5,△APC的面积是10,△ABC的面积是15,求△ABC的周长.
11.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系.并说明理由.
12.如图,在△ABC中,AD是它的角平分线.求证:S△ABD:S△ACD=AB:AC.
(1)在图1中完成上面的证明过程;
(2)在图2中,AD是△ABC外角平分线,如果AB=10,AC=4,BC=7,求BD的长.
13.如图,在△ABE中,D、C分别在AE、BE上且CD=CB,AC平分∠EAB,CH⊥AB于点H.
(1)求证:∠ADC+∠B=180°;
(2)若AD=3,AB=9,求AH的长.
14.如图,在∠AOB的两边OA、OB上分别取点M、N,连接MN.若MP平分∠AMN,NP平分∠MNB.
(1)求证:OP平分∠AOB;
(2)若MN=8,且△PMN与△OMN的面积分别是16和24,求线段OM与ON的长度之和.
15.如图,四边形ABCD中,∠B=∠C=90°,点E为BC的中点,且AE平分∠BAD.
(1)求证:DE平分∠ADC;
(2)求证:AB+CD=AD.
16.如图,△ABC中,点D在边BC延长线上,∠ACB=100°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=50°.
(1)求∠ACE的度数;
(2)求证:AE平分∠CAF;
(3)若AC+CD=14,AB=10,且S△ACD=21,求△ABE的面积.
17.如图①,在△ABC中,∠ABC和∠ACB的平分线交于点O,∠A=α.
(1)如图①,若∠A=50°,求∠BOC的度数.
(2)如图②,连接OA,求证:AO平分∠BAC.
(3)如图③,若射线BO与∠ACB的外角平分线交于点P,求证OC⊥PC.
18.如图,在△ABC中,O为∠ABC,∠ACB的平分线的交点OD⊥AB,OE⊥AC,OF⊥BC,垂足分别为D,E,F.
(1)求证:AO平分∠BAC;
(2)若△ABC的周长是30,△ABC的面积为45,求OF的长.
19.在△ABC中,AE、BF是角平分线,交于O点.
(1)如图1,AD是高,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的度数.
(2)如图2,若OE=OF,AC≠BC,求∠C的度数.
(3)如图3,若∠C=90°,BC=8,AC=6,AB=10,求S△AOB.
参考答案
1.【解答】解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三个外角两两平分线的交点,共三处.
故选:D.
2.【解答】解:设△ABD的边AB上的高与△ACD的AC上的高分别为h1,h2,
∵在△ABC中,AD是它的角平分线,
∴h1=h2,
∴△ABD与△ACD的面积之比
=4:3.
故选:B.
3.【解答】解:作DE⊥AB于点E,
,
由题意可知,AD是∠CAB的平分线,
∵∠C=90°,
∴DC⊥AC,
∵DE⊥AB,CD=6,
∴DE=CD=6,
∵AB=15,
∴,
故选:C.
4.【解答】解:过点P作PE⊥BC于E,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,
∵BP和CP分别平分∠ABC和∠DCB,AD⊥AB,AD⊥CD,PE⊥BC,
∴PA=PE=PD,
∵AD=10,
∴PE=5,即点P到BC的距离是5,
故选:D.
5.【解答】解:作PN⊥OB于N,
∵OP平分∠AOB,PF⊥OA,PN⊥OB,
∴PF=PN=3.5,
∵S△ODPOP×DHOD×PN,
∴8×DH4×3.5,
解得,DH,
故选:D.
6.【解答】解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵点O是内心,
∴OE=OF=OD,
∴S△ABO:S△BCO:S△CAO AB OE: BC OF: AC OD=AB:BC:AC=2:3:4,
故选:C.
7.【解答】解:过点D作DF⊥AC于F,
∵AD是的角平分线,DE⊥AB,
∴DE=DF=2,
∴S△ABC=S△ABD+S△ADCAB DEAC DF4×2AC×2=7,
解得AC=3.
故选:A.
8.【解答】解:∵点I是△ABC三条角平分线的交点,
∴△ABI、△ACI和△BCI的边AB、AC和BC边上的高相等,
设△ABI、△ACI和△BCI的高为h,
∴,,
由三角形三边关系得AB+AC>BC,
∴S1+S2>S3,
又∵S3=10,
∴S1+S2>10,故S1+S2的值可能为14,选项C符合题意,
选项A、B、D不符合题意.
故选:C.
9.【解答】解:∵∠BAC=90°,BD平分∠ABC,DE⊥BC,
∴AD=DE,
在Rt△ABD和Rt△EBD中,
,
∴Rt△ABD≌Rt△EBD(HL),
∴AB=BE,
∵△ABC与△CDE的周长分别为13和3,
∴AB+BC+AC=AB+AC+BE+EC=13,DE+EC+DC=AD+EC+DC=AC+EC=3,
∴AB+BE=10,
∴AB=BE=5.
故选:D.
10.【解答】(1)证明:如图,过点P作PF⊥BD于F,PG⊥AC于G,PH⊥BE于H,
∵AP平分∠DAC,PF⊥BD,PG⊥AC,
∴PF=PG,
∵CP平分∠ACE,PH⊥BE,PG⊥AC,
∴PH=PG,
∴PF=PH,
∵PF⊥BD,PH⊥BE,
∴BP平分∠ABC;
(2)∵AC=5,△APC的面积是10,
∴5×PG=10,
∴PG=4,
∴PF=PH=PG=4,
∵△ABC的面积是15,△APC的面积是10,
∴AB×PFBC×PH=25,
∴AB+BC=12.5,
∴△ABC的周长=AB+BC+AC=12.5+5=17.5.
11.【解答】(1)证明:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△FCD和Rt△BED中,
,
∴Rt△FCD≌Rt△BED(HL),
∴CF=EB;
(2)解:AB=AF+2BE,
理由如下:在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴AB=AE+BE=AF+FC+BE=AF+2BE.
12.【解答】(1)证明:如图1中,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠ABC,
∴DE=DF,
∴;
(2)解:如图2中,过点D作DM⊥AE于点M,DN⊥AC于点N.
∵AD平分∠EAC,
∴DM=DN,
∴,
∴,
∴,
∴CD,
∴BD=BC+CD=7.
13.【解答】(1)证明:过点C作CM⊥DE,垂足为M,
∵AC平分∠EAB,CH⊥AB,CM⊥DE,
∴CM=CH,∠CMA=∠CHB=90°,
在Rt△DMC与Rt△BHC中
,
∴Rt△DMC≌Rt△BHC(HL),
∴DM=BH,∠1=∠B,
∵∠1+∠CDA=180°,
∴∠ADC+∠B=180°;
(2)解:∵∠CMA=∠CHB=90°,
在Rt△AMC与Rt△AHC中
,
∴Rt△AMC≌Rt△AHC(HL),
∴AM=AH,
设BH=DM=x,
则AH=9﹣x,AM=3+x,
∴9﹣x=3+x,
解得x=3,
∴AH=6.
14.【解答】(1)证明:过点P作PC⊥OA,垂足为C,过点P作PD⊥MN,垂足为D,过点P作PE⊥OB,垂足为E,
∵MP平分∠AMN,PC⊥OA,PD⊥MN,
∴PC=PD,
∵NP平分∠MNB,PD⊥MN,PE⊥OB,
∴PD=PE,
∴PC=PE,
∴OP平分∠AOB;
(2)∵△PMN的面积是16,MN=8,
∴MN PD=16,
∴8 PD=16,
∴PD=4,
∴PD=PC=PE=4,
∵△OMN的面积是24,
∴四边形MONP的面积=△PMN的面积+△OMN的面积=16+24=40,
∴△POM的面积+△PON的面积=40,
∴OM PCON PE=40,
∴OM 4ON 4=40,
∴OM+ON=20,
∴线段OM与ON的长度之和为20.
15.【解答】证明:(1)如图,过点E作EF⊥AD于F,
∵∠B=90°,AE平分∠DAB,
∴BE=EF,
∵E是BC的中点,
∴BE=CE,
∴CE=EF,
又∵∠C=90°,EF⊥AD,
∴DE是∠ADC的平分线.
(2)∵AE平分∠BAD,DE平分∠ADC,EF⊥AD,∠B=∠C=90°,
∴AB=AF,DC=DF,
∴AB+CD=AF+FD=AD.
16.【解答】解:(1)∵∠ACB=100°,
∴∠ACD=180°﹣100°=80°,
∵EH⊥BD,
∴∠CHE=90°,
∵∠CEH=50°,
∴∠ECH=90°﹣50°=40°,
∴∠ACE=∠ACD﹣∠ECH=80°﹣40°=40°.
(2)证明:如图:过E点分别作EM⊥BF于M,EN⊥AC与N,
∵BE平分∠ABC,
∴EM=EH,
∵∠ACE=∠ECH=40°,
∴CE平分∠ACD,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF.
(3)解:∵AC+CD=14,S△ACD=21,EM=EN=EH,
∴,
即,解得EM=3,
∵AB=10,
∴.
17.【解答】(1)解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=130°,
∵∠ABC和∠ACB的平分线交于点O,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB∠ABC∠ACB=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°;
(2)证明:过点O作OD⊥BC,OE⊥AB,OF⊥AC,垂足分别为D,E,F,
∵∠ABC和∠ACB的平分线交于点O,OD⊥BC,OE⊥AB,OF⊥AC,
∴OD=OE,OD=OF,
∴OE=OF,
∴OA平分∠BAC;
(3)证明:∵OC平分∠ACB,CP平分∠ACD,
∴∠ACO∠ACB,∠ACP∠ACD,
∴∠OCP=∠ACO+∠ACP
∠ACB∠ACD
∠BCD
180°
=90°,
∴OC⊥CP.
18.【解答】(1)证明:如图,连接OA,
∵OB为∠ABC的平分线,OD⊥AB,OF⊥BC,
∴OD=OF,
∵OC为∠ACB的平分线的交点OE⊥AC,OF⊥BC,
∴OE=OF,
∴OD=OE=OF
在Rt△AOD与Rt△AOE中,,
∴Rt△AOD≌Rt△AOE(HL)
∴∠OAD=∠OAE,
∴AO平分∠BAC.
(2)解:由(1)知OD=OE=OF,
∴S△AOB+S△BOC+S△AOC,
∵S△ABC=45,AB+BC+AC=30,
∴,
∴OF=3.
19.【解答】解:(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°﹣90°﹣70°=20°;
∵∠BAC=50°,∠C=70°,
∴∠BAO=25°,∠ABC=60°,
∵BF是∠ABC的角平分线,
∴∠ABO=30°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°;
(2)连接OC,
∵AE、BF是角平分线,交于O点,
∴OC是∠ACB的角平分线,
∴∠OCF=∠OCE,
过O作OM⊥BC,ON⊥AC,
则OM=ON,
在Rt△OEM与Rt△OFN中,,
∴Rt△OEM≌Rt△OFN,(HL),
∴∠EOM=∠FON,
∴∠MON=∠EOF=180°﹣∠ACB,
∵AE、BF是角平分线,
∴∠AOB=90°∠ACB,
即90°∠ACB=180°﹣∠ACB,
∴∠ACB=60°;
(3)连接OC,过O作OD⊥AB于D,OG⊥BC于G,OH⊥AC于H,
∵AE、BF是角平分线,交于O点,
∴OD=OG=OH,
∴S△ABC8×610OD6×OG8×OH,
∴OD=2,
∴S△AOB10×2=10.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
