2025华东师大版初中数学七年级下册单元练--第6章 单元检测卷(含答案)
文档属性
| 名称 | 2025华东师大版初中数学七年级下册单元练--第6章 单元检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 497.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 06:09:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025华东师大版初中数学七年级下册
第6章 单元检测卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列方程是二元一次方程的是( )
A.xy+1=0 B.x+2y=3
C.y+=2 D.x2+y=1
2.解方程组最恰当的方法是( )
A.由①得y=3x-2,再代入②
B.由②得3x=11-2y,再代入①
C.由②-①,消去x
D.由①×2+②,消去y
3.三元一次方程x-y+z=3有无数个解,下列四组值中,不是该方程的解的是( )
A. B.
C. D.
4.设y=kx+b,当x=1时,y=1;当x=2时,y=-2,则k,b的值分别为( )
A.-1,2 B.-3,4 C.1,0 D.-5,6
5.已知是方程组的解,则a-b的值是( )
A.-1 B.2 C.3 D.4
6.小红同学在解关于x和y的二元一次方程组时,利用①-②就将未知数y消去了,则m和n应该满足的条件是( )
A.m=n B.m+n=0
C.m+n=1 D.mn=1
7.小明在如图所示的3×3的方格内填入了一些数,若图中各行、各列及各对角线上的三个数之和都相等,则x+y的值为( )
A.6 B.8 C.10 D.12
8.《九章算术》是我国古代的一部数学经典著作,在它的“方程”一章里,一次方程组是由算筹布置而成的.图1中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项,把如图1所示的算筹图用我们现在熟悉的方程组形式表示出来,就是类似地,若如图2所示的算筹图列出的方程组解得x=3,则图2中的“?”所表示的算筹为( )
A. B. C. D.
9.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共需64元;若购买甲4件、乙10件、丙1件,共需79元.现购买甲、乙、丙各一件,共需( )
A.33元 B.34元 C.35元 D.36元
10.对于有理数x,y定义一种新运算“□”:x□y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法与乘法运算.已知3□5=15,4□7=28,则1□1的值为( )
A.-1 B.-11 C.1 D.11
二、填空题(本大题共6小题,每小题5分,满分30分)
11.若(a-1)x+5+2z2-|a|=10是一个关于x,y,z的三元一次方程,则a= ,b= .
12.《九章算术》是中国古代重要的数学著作,其中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”设能买醇酒x斗,行酒y斗,可列二元一次方程组为 .
13.小林、小芳和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图所示,则小亮的得分是 .
14.解关于x,y的方程组时,小明看错了c,解得而正确答案是则a= ,b= ,c= .
15.已知关于x,y的二元一次方程组的解满足x+y=3m,则m= .
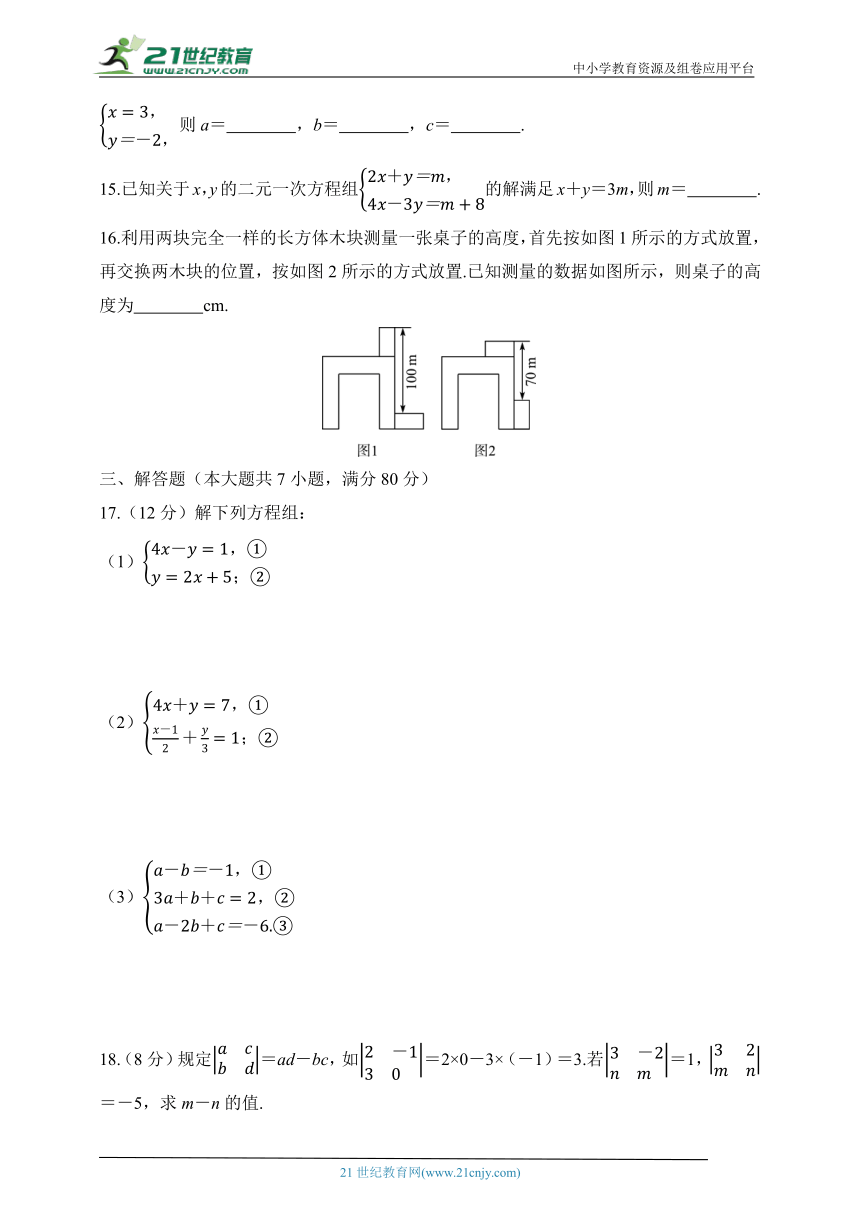
16.利用两块完全一样的长方体木块测量一张桌子的高度,首先按如图1所示的方式放置,再交换两木块的位置,按如图2所示的方式放置.已知测量的数据如图所示,则桌子的高度为 cm.
三、解答题(本大题共7小题,满分80分)
17.(12分)解下列方程组:
(1)
(2)
(3)
18.(8分)规定=ad-bc,如=2×0-3×(-1)=3.若=1,=-5,求m-n的值.
19.(10分)已知二元一次方程2x+5y=24.
(1)写出此方程的所有正整数解;
(2)若二元一次方程组存在x,y互为相反数的解,请在括号处补上一个方程,并写出此方程组的解.
20.(10分)数学活动课上,小云和小辉在讨论老师给出的一个问题:“已知关于x,y的二元一次方程组的解满足2x+3y=1③,求m的值.”他们的部分对话如图所示.
请根据提供的信息,解答下列问题:
(1)按照小云的方法求得x的值为 ,y的值为 ;
(2)老师说小辉的方法体现了整体代入的思想,请你按照小辉的思路求出m的值.
21.(12分)为落实教育部门关于“在校学生每天锻炼时间不少于1小时”的文件精神,提升学生身体素质,某校利用课后服务时间,在七年级开展“体育赋能,助力成长”班级篮球赛,共16个班级参加.
(1)比赛积分规定:每场比赛都要分出胜负,胜一场积3分,负一场积1分.某班在12场比赛中获得总积分30分,求该班胜、负场数分别是多少场.
(2)根据比赛情况,学校商店对某篮球在甲、乙两校区的销售单价进行了如下调整:甲校区上涨10%,乙校区降价5元.已知该篮球的销售单价调整前甲校区比乙校区少10元,调整后甲校区比乙校区少1元,求调整前甲、乙两校区该篮球的销售单价.
22.(14分)[阅读理解]在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化繁为简.
(1)解方程组 解:把②代入①,得x+2×1=3,解得x=1. 把x=1代入②,得y=0.∴方程组的解为
(2)已知求x+y+z的值. 解:①+②,得10x+10y+10z=40.③ ③÷10,得x+y+z=4.
[类比迁移]
(1)直接写出方程组的解.
(2)若求x+y+z的值.
[实际应用]打折前,买36件A商品、12件B商品用了960元.打折后,买45件A商品、15件B商品用了1 100元,求打折比不打折少花了多少钱.
23.(14分)小林在某商店购买A,B两种商品若干次(每次A,B两种商品都购买),其中第一、二次购买时,均按标价购买;第三次购买时,A,B两种商品同时打折.三次购买A,B两种商品的数量和费用如表所示.
购买A商品的数量/个 购买B商品的数量/个 总费用/元
第一次购买 6 5 980
第二次购买 3 7 940
第三次购买 9 8 912
(1)求A,B两种商品的标价.
(2)若A,B两种商品的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若小林第四次购买共花去了960元,则小林有哪几种购买方案?
第6章 单元检测卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列方程是二元一次方程的是( B )
A.xy+1=0 B.x+2y=3
C.y+=2 D.x2+y=1
2.解方程组最恰当的方法是( C )
A.由①得y=3x-2,再代入②
B.由②得3x=11-2y,再代入①
C.由②-①,消去x
D.由①×2+②,消去y
3.三元一次方程x-y+z=3有无数个解,下列四组值中,不是该方程的解的是( D )
A. B.
C. D.
4.设y=kx+b,当x=1时,y=1;当x=2时,y=-2,则k,b的值分别为( B )
A.-1,2 B.-3,4 C.1,0 D.-5,6
5.已知是方程组的解,则a-b的值是( D )
A.-1 B.2 C.3 D.4
6.小红同学在解关于x和y的二元一次方程组时,利用①-②就将未知数y消去了,则m和n应该满足的条件是( B )
A.m=n B.m+n=0
C.m+n=1 D.mn=1
7.小明在如图所示的3×3的方格内填入了一些数,若图中各行、各列及各对角线上的三个数之和都相等,则x+y的值为( C )
A.6 B.8 C.10 D.12
8.《九章算术》是我国古代的一部数学经典著作,在它的“方程”一章里,一次方程组是由算筹布置而成的.图1中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项,把如图1所示的算筹图用我们现在熟悉的方程组形式表示出来,就是类似地,若如图2所示的算筹图列出的方程组解得x=3,则图2中的“?”所表示的算筹为( B )
A. B. C. D.
9.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共需64元;若购买甲4件、乙10件、丙1件,共需79元.现购买甲、乙、丙各一件,共需( B )
A.33元 B.34元 C.35元 D.36元
10.对于有理数x,y定义一种新运算“□”:x□y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法与乘法运算.已知3□5=15,4□7=28,则1□1的值为( B )
A.-1 B.-11 C.1 D.11
二、填空题(本大题共6小题,每小题5分,满分30分)
11.若(a-1)x+5+2z2-|a|=10是一个关于x,y,z的三元一次方程,则a= -1 ,b= 0 .
12.《九章算术》是中国古代重要的数学著作,其中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”设能买醇酒x斗,行酒y斗,可列二元一次方程组为 .
13.小林、小芳和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图所示,则小亮的得分是 21 .
14.解关于x,y的方程组时,小明看错了c,解得而正确答案是则a= 4 ,b= 5 ,c= -2 .
15.已知关于x,y的二元一次方程组的解满足x+y=3m,则m= - .
16.利用两块完全一样的长方体木块测量一张桌子的高度,首先按如图1所示的方式放置,再交换两木块的位置,按如图2所示的方式放置.已知测量的数据如图所示,则桌子的高度为 85 cm.
三、解答题(本大题共7小题,满分80分)
17.(12分)解下列方程组:
(1)
解:把②代入①,得4x-(2x+5)=1.
整理,得2x=6,解得 x=3.
把x=3代入②,得y=2×3+5,解得y=11.
∴原方程组的解为
(2)
解:由②,得3x+2y=9.③
①×2-③,得5x=5,解得x=1.
把x=1代入①,得4+y=7,解得y=3.
∴原方程组的解为
(3)
解:②-③,得2a+3b=8.④
④-①×2,得5b=10,解得b=2.
把b=2代入①,得a-2=-1,解得a=1.
把a=1,b=2代入②,得3+2+c=2,
解得c=-3.
∴原方程组的解为
18.(8分)规定=ad-bc,如=2×0-3×(-1)=3.若=1,=-5,求m-n的值.
解:∵=1,=-5,
∴
①×2+②×3,得13n=-13,解得n=-1.
把n=-1代入①,得3m-2=1,解得m=1.
∴m-n=1-(-1)=2,
即m-n的值为2.
19.(10分)已知二元一次方程2x+5y=24.
(1)写出此方程的所有正整数解;
(2)若二元一次方程组存在x,y互为相反数的解,请在括号处补上一个方程,并写出此方程组的解.
解:(1)或
(2)∵方程组的解互为相反数,∴x=-y.
把x=-y代入2x+5y=24,得-2y+5y=24,
解得y=8,∴x=-8.
∵2×(-8)+3×8=-16+24=8,
∴括号处补的方程为2x+3y=8(答案不唯一),
此方程组的解为
20.(10分)数学活动课上,小云和小辉在讨论老师给出的一个问题:“已知关于x,y的二元一次方程组的解满足2x+3y=1③,求m的值.”他们的部分对话如图所示.
请根据提供的信息,解答下列问题:
(1)按照小云的方法求得x的值为 5 ,y的值为 -3 ;
(2)老师说小辉的方法体现了整体代入的思想,请你按照小辉的思路求出m的值.
解:①+②,得4x+6y=5-3m,
即2(2x+3y)=5-3m,
∵2x+3y=1,∴2×1=5-3m,
解得m=1.
21.(12分)为落实教育部门关于“在校学生每天锻炼时间不少于1小时”的文件精神,提升学生身体素质,某校利用课后服务时间,在七年级开展“体育赋能,助力成长”班级篮球赛,共16个班级参加.
(1)比赛积分规定:每场比赛都要分出胜负,胜一场积3分,负一场积1分.某班在12场比赛中获得总积分30分,求该班胜、负场数分别是多少场.
(2)根据比赛情况,学校商店对某篮球在甲、乙两校区的销售单价进行了如下调整:甲校区上涨10%,乙校区降价5元.已知该篮球的销售单价调整前甲校区比乙校区少10元,调整后甲校区比乙校区少1元,求调整前甲、乙两校区该篮球的销售单价.
解:(1)设该班胜了x场,负了y场.
根据题意,得解得
答:该班胜了9场,负了3场.
(2)设调整前甲校区该商品的销售单价为x元,乙校区该商品的销售单价为y元.
由题意,得解得
答:调整前甲校区该篮球的销售单价为40元,乙校区该篮球的销售单价为50元.
22.(14分)[阅读理解]在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化繁为简.
(1)解方程组 解:把②代入①,得x+2×1=3,解得x=1. 把x=1代入②,得y=0.∴方程组的解为
(2)已知求x+y+z的值. 解:①+②,得10x+10y+10z=40.③ ③÷10,得x+y+z=4.
[类比迁移]
(1)直接写出方程组的解.
(2)若求x+y+z的值.
[实际应用]打折前,买36件A商品、12件B商品用了960元.打折后,买45件A商品、15件B商品用了1 100元,求打折比不打折少花了多少钱.
解:[类比迁移]
(1)方程组的解为
(2)①-②,得4x+4y+4z=4.③
③÷4,得x+y+z=1.
[实际应用]设打折前A商品每件x元,B商品每件y元.
根据题意,得36x+12y=960.
两边同时乘以,得45x+15y=1 200.
1 200-1 100=100(元).
答:打折比不打折少花了100元.
23.(14分)小林在某商店购买A,B两种商品若干次(每次A,B两种商品都购买),其中第一、二次购买时,均按标价购买;第三次购买时,A,B两种商品同时打折.三次购买A,B两种商品的数量和费用如表所示.
购买A商品的数量/个 购买B商品的数量/个 总费用/元
第一次购买 6 5 980
第二次购买 3 7 940
第三次购买 9 8 912
(1)求A,B两种商品的标价.
(2)若A,B两种商品的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若小林第四次购买共花去了960元,则小林有哪几种购买方案?
解:(1)设A商品的标价为x元/个,B商品的标价为y元/个.
根据题意,得解得
答:A商品的标价为80元/个,B商品的标价为100元/个.
(2)912÷(80×9+100×8)×10=6.
答:商店是打六折出售这两种商品的.
(3)设小林购买m个A商品,n个B商品.
根据题意,得80×0.6m+100×0.6n=960,
∴m=20-n.
当n=4时,m=15;
当n=8时,m=10;
当n=12时,m=5.
答:小林共有三种购买方案,方案一:购买15个A商品,4个B商品;方案二:购买10个A商品,8个B商品;方案三:购买5个A商品,12个B商品.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025华东师大版初中数学七年级下册
第6章 单元检测卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列方程是二元一次方程的是( )
A.xy+1=0 B.x+2y=3
C.y+=2 D.x2+y=1
2.解方程组最恰当的方法是( )
A.由①得y=3x-2,再代入②
B.由②得3x=11-2y,再代入①
C.由②-①,消去x
D.由①×2+②,消去y
3.三元一次方程x-y+z=3有无数个解,下列四组值中,不是该方程的解的是( )
A. B.
C. D.
4.设y=kx+b,当x=1时,y=1;当x=2时,y=-2,则k,b的值分别为( )
A.-1,2 B.-3,4 C.1,0 D.-5,6
5.已知是方程组的解,则a-b的值是( )
A.-1 B.2 C.3 D.4
6.小红同学在解关于x和y的二元一次方程组时,利用①-②就将未知数y消去了,则m和n应该满足的条件是( )
A.m=n B.m+n=0
C.m+n=1 D.mn=1
7.小明在如图所示的3×3的方格内填入了一些数,若图中各行、各列及各对角线上的三个数之和都相等,则x+y的值为( )
A.6 B.8 C.10 D.12
8.《九章算术》是我国古代的一部数学经典著作,在它的“方程”一章里,一次方程组是由算筹布置而成的.图1中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项,把如图1所示的算筹图用我们现在熟悉的方程组形式表示出来,就是类似地,若如图2所示的算筹图列出的方程组解得x=3,则图2中的“?”所表示的算筹为( )
A. B. C. D.
9.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共需64元;若购买甲4件、乙10件、丙1件,共需79元.现购买甲、乙、丙各一件,共需( )
A.33元 B.34元 C.35元 D.36元
10.对于有理数x,y定义一种新运算“□”:x□y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法与乘法运算.已知3□5=15,4□7=28,则1□1的值为( )
A.-1 B.-11 C.1 D.11
二、填空题(本大题共6小题,每小题5分,满分30分)
11.若(a-1)x+5+2z2-|a|=10是一个关于x,y,z的三元一次方程,则a= ,b= .
12.《九章算术》是中国古代重要的数学著作,其中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”设能买醇酒x斗,行酒y斗,可列二元一次方程组为 .
13.小林、小芳和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图所示,则小亮的得分是 .
14.解关于x,y的方程组时,小明看错了c,解得而正确答案是则a= ,b= ,c= .
15.已知关于x,y的二元一次方程组的解满足x+y=3m,则m= .
16.利用两块完全一样的长方体木块测量一张桌子的高度,首先按如图1所示的方式放置,再交换两木块的位置,按如图2所示的方式放置.已知测量的数据如图所示,则桌子的高度为 cm.
三、解答题(本大题共7小题,满分80分)
17.(12分)解下列方程组:
(1)
(2)
(3)
18.(8分)规定=ad-bc,如=2×0-3×(-1)=3.若=1,=-5,求m-n的值.
19.(10分)已知二元一次方程2x+5y=24.
(1)写出此方程的所有正整数解;
(2)若二元一次方程组存在x,y互为相反数的解,请在括号处补上一个方程,并写出此方程组的解.
20.(10分)数学活动课上,小云和小辉在讨论老师给出的一个问题:“已知关于x,y的二元一次方程组的解满足2x+3y=1③,求m的值.”他们的部分对话如图所示.
请根据提供的信息,解答下列问题:
(1)按照小云的方法求得x的值为 ,y的值为 ;
(2)老师说小辉的方法体现了整体代入的思想,请你按照小辉的思路求出m的值.
21.(12分)为落实教育部门关于“在校学生每天锻炼时间不少于1小时”的文件精神,提升学生身体素质,某校利用课后服务时间,在七年级开展“体育赋能,助力成长”班级篮球赛,共16个班级参加.
(1)比赛积分规定:每场比赛都要分出胜负,胜一场积3分,负一场积1分.某班在12场比赛中获得总积分30分,求该班胜、负场数分别是多少场.
(2)根据比赛情况,学校商店对某篮球在甲、乙两校区的销售单价进行了如下调整:甲校区上涨10%,乙校区降价5元.已知该篮球的销售单价调整前甲校区比乙校区少10元,调整后甲校区比乙校区少1元,求调整前甲、乙两校区该篮球的销售单价.
22.(14分)[阅读理解]在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化繁为简.
(1)解方程组 解:把②代入①,得x+2×1=3,解得x=1. 把x=1代入②,得y=0.∴方程组的解为
(2)已知求x+y+z的值. 解:①+②,得10x+10y+10z=40.③ ③÷10,得x+y+z=4.
[类比迁移]
(1)直接写出方程组的解.
(2)若求x+y+z的值.
[实际应用]打折前,买36件A商品、12件B商品用了960元.打折后,买45件A商品、15件B商品用了1 100元,求打折比不打折少花了多少钱.
23.(14分)小林在某商店购买A,B两种商品若干次(每次A,B两种商品都购买),其中第一、二次购买时,均按标价购买;第三次购买时,A,B两种商品同时打折.三次购买A,B两种商品的数量和费用如表所示.
购买A商品的数量/个 购买B商品的数量/个 总费用/元
第一次购买 6 5 980
第二次购买 3 7 940
第三次购买 9 8 912
(1)求A,B两种商品的标价.
(2)若A,B两种商品的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若小林第四次购买共花去了960元,则小林有哪几种购买方案?
第6章 单元检测卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列方程是二元一次方程的是( B )
A.xy+1=0 B.x+2y=3
C.y+=2 D.x2+y=1
2.解方程组最恰当的方法是( C )
A.由①得y=3x-2,再代入②
B.由②得3x=11-2y,再代入①
C.由②-①,消去x
D.由①×2+②,消去y
3.三元一次方程x-y+z=3有无数个解,下列四组值中,不是该方程的解的是( D )
A. B.
C. D.
4.设y=kx+b,当x=1时,y=1;当x=2时,y=-2,则k,b的值分别为( B )
A.-1,2 B.-3,4 C.1,0 D.-5,6
5.已知是方程组的解,则a-b的值是( D )
A.-1 B.2 C.3 D.4
6.小红同学在解关于x和y的二元一次方程组时,利用①-②就将未知数y消去了,则m和n应该满足的条件是( B )
A.m=n B.m+n=0
C.m+n=1 D.mn=1
7.小明在如图所示的3×3的方格内填入了一些数,若图中各行、各列及各对角线上的三个数之和都相等,则x+y的值为( C )
A.6 B.8 C.10 D.12
8.《九章算术》是我国古代的一部数学经典著作,在它的“方程”一章里,一次方程组是由算筹布置而成的.图1中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项,把如图1所示的算筹图用我们现在熟悉的方程组形式表示出来,就是类似地,若如图2所示的算筹图列出的方程组解得x=3,则图2中的“?”所表示的算筹为( B )
A. B. C. D.
9.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共需64元;若购买甲4件、乙10件、丙1件,共需79元.现购买甲、乙、丙各一件,共需( B )
A.33元 B.34元 C.35元 D.36元
10.对于有理数x,y定义一种新运算“□”:x□y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法与乘法运算.已知3□5=15,4□7=28,则1□1的值为( B )
A.-1 B.-11 C.1 D.11
二、填空题(本大题共6小题,每小题5分,满分30分)
11.若(a-1)x+5+2z2-|a|=10是一个关于x,y,z的三元一次方程,则a= -1 ,b= 0 .
12.《九章算术》是中国古代重要的数学著作,其中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”设能买醇酒x斗,行酒y斗,可列二元一次方程组为 .
13.小林、小芳和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图所示,则小亮的得分是 21 .
14.解关于x,y的方程组时,小明看错了c,解得而正确答案是则a= 4 ,b= 5 ,c= -2 .
15.已知关于x,y的二元一次方程组的解满足x+y=3m,则m= - .
16.利用两块完全一样的长方体木块测量一张桌子的高度,首先按如图1所示的方式放置,再交换两木块的位置,按如图2所示的方式放置.已知测量的数据如图所示,则桌子的高度为 85 cm.
三、解答题(本大题共7小题,满分80分)
17.(12分)解下列方程组:
(1)
解:把②代入①,得4x-(2x+5)=1.
整理,得2x=6,解得 x=3.
把x=3代入②,得y=2×3+5,解得y=11.
∴原方程组的解为
(2)
解:由②,得3x+2y=9.③
①×2-③,得5x=5,解得x=1.
把x=1代入①,得4+y=7,解得y=3.
∴原方程组的解为
(3)
解:②-③,得2a+3b=8.④
④-①×2,得5b=10,解得b=2.
把b=2代入①,得a-2=-1,解得a=1.
把a=1,b=2代入②,得3+2+c=2,
解得c=-3.
∴原方程组的解为
18.(8分)规定=ad-bc,如=2×0-3×(-1)=3.若=1,=-5,求m-n的值.
解:∵=1,=-5,
∴
①×2+②×3,得13n=-13,解得n=-1.
把n=-1代入①,得3m-2=1,解得m=1.
∴m-n=1-(-1)=2,
即m-n的值为2.
19.(10分)已知二元一次方程2x+5y=24.
(1)写出此方程的所有正整数解;
(2)若二元一次方程组存在x,y互为相反数的解,请在括号处补上一个方程,并写出此方程组的解.
解:(1)或
(2)∵方程组的解互为相反数,∴x=-y.
把x=-y代入2x+5y=24,得-2y+5y=24,
解得y=8,∴x=-8.
∵2×(-8)+3×8=-16+24=8,
∴括号处补的方程为2x+3y=8(答案不唯一),
此方程组的解为
20.(10分)数学活动课上,小云和小辉在讨论老师给出的一个问题:“已知关于x,y的二元一次方程组的解满足2x+3y=1③,求m的值.”他们的部分对话如图所示.
请根据提供的信息,解答下列问题:
(1)按照小云的方法求得x的值为 5 ,y的值为 -3 ;
(2)老师说小辉的方法体现了整体代入的思想,请你按照小辉的思路求出m的值.
解:①+②,得4x+6y=5-3m,
即2(2x+3y)=5-3m,
∵2x+3y=1,∴2×1=5-3m,
解得m=1.
21.(12分)为落实教育部门关于“在校学生每天锻炼时间不少于1小时”的文件精神,提升学生身体素质,某校利用课后服务时间,在七年级开展“体育赋能,助力成长”班级篮球赛,共16个班级参加.
(1)比赛积分规定:每场比赛都要分出胜负,胜一场积3分,负一场积1分.某班在12场比赛中获得总积分30分,求该班胜、负场数分别是多少场.
(2)根据比赛情况,学校商店对某篮球在甲、乙两校区的销售单价进行了如下调整:甲校区上涨10%,乙校区降价5元.已知该篮球的销售单价调整前甲校区比乙校区少10元,调整后甲校区比乙校区少1元,求调整前甲、乙两校区该篮球的销售单价.
解:(1)设该班胜了x场,负了y场.
根据题意,得解得
答:该班胜了9场,负了3场.
(2)设调整前甲校区该商品的销售单价为x元,乙校区该商品的销售单价为y元.
由题意,得解得
答:调整前甲校区该篮球的销售单价为40元,乙校区该篮球的销售单价为50元.
22.(14分)[阅读理解]在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化繁为简.
(1)解方程组 解:把②代入①,得x+2×1=3,解得x=1. 把x=1代入②,得y=0.∴方程组的解为
(2)已知求x+y+z的值. 解:①+②,得10x+10y+10z=40.③ ③÷10,得x+y+z=4.
[类比迁移]
(1)直接写出方程组的解.
(2)若求x+y+z的值.
[实际应用]打折前,买36件A商品、12件B商品用了960元.打折后,买45件A商品、15件B商品用了1 100元,求打折比不打折少花了多少钱.
解:[类比迁移]
(1)方程组的解为
(2)①-②,得4x+4y+4z=4.③
③÷4,得x+y+z=1.
[实际应用]设打折前A商品每件x元,B商品每件y元.
根据题意,得36x+12y=960.
两边同时乘以,得45x+15y=1 200.
1 200-1 100=100(元).
答:打折比不打折少花了100元.
23.(14分)小林在某商店购买A,B两种商品若干次(每次A,B两种商品都购买),其中第一、二次购买时,均按标价购买;第三次购买时,A,B两种商品同时打折.三次购买A,B两种商品的数量和费用如表所示.
购买A商品的数量/个 购买B商品的数量/个 总费用/元
第一次购买 6 5 980
第二次购买 3 7 940
第三次购买 9 8 912
(1)求A,B两种商品的标价.
(2)若A,B两种商品的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若小林第四次购买共花去了960元,则小林有哪几种购买方案?
解:(1)设A商品的标价为x元/个,B商品的标价为y元/个.
根据题意,得解得
答:A商品的标价为80元/个,B商品的标价为100元/个.
(2)912÷(80×9+100×8)×10=6.
答:商店是打六折出售这两种商品的.
(3)设小林购买m个A商品,n个B商品.
根据题意,得80×0.6m+100×0.6n=960,
∴m=20-n.
当n=4时,m=15;
当n=8时,m=10;
当n=12时,m=5.
答:小林共有三种购买方案,方案一:购买15个A商品,4个B商品;方案二:购买10个A商品,8个B商品;方案三:购买5个A商品,12个B商品.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
