北师版七年级数学下册第四章第二、三节专项训练题
文档属性
| 名称 | 北师版七年级数学下册第四章第二、三节专项训练题 |  | |
| 格式 | zip | ||
| 文件大小 | 167.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-05 22:15:39 | ||
图片预览


文档简介
北师版七年级数学下册第四章第二、三节专项训练题
一.选择题(共12小题)
1.(2015 百色)下列图形中具有稳定性的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
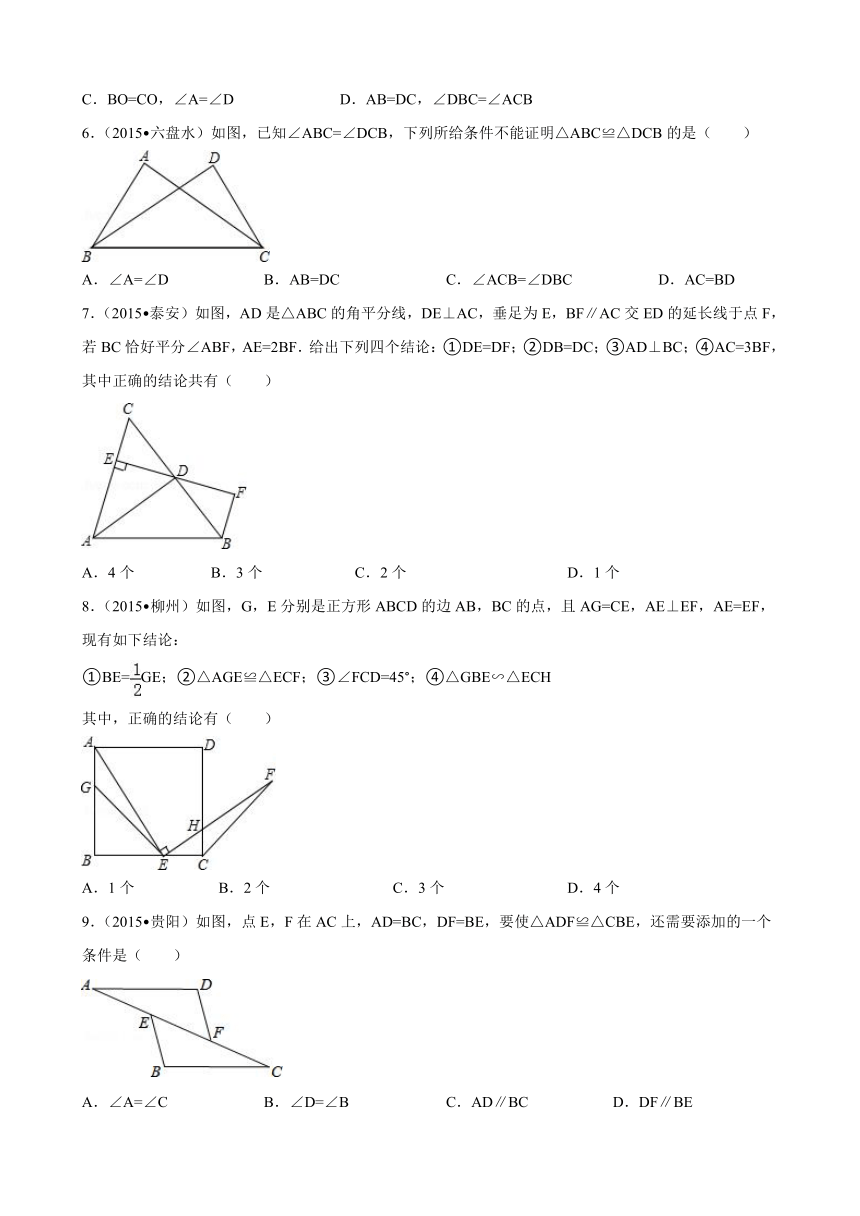
2.(2015 莆田)如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
( http: / / www.21cnjy.com )
A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC
3.(2015 宜昌)如图,在方格纸中, ( http: / / www.21cnjy.com )以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
4.(2015 宁波)如图, ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
( http: / / www.21cnjy.com )
A.BE=DF B.BF=DE C.AE=CF D.∠1=∠2
5.(2015 海南)如图,下列条件中,不能证明△ABC≌△DCB的是( )
( http: / / www.21cnjy.com )
A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D D.AB=DC,∠DBC=∠ACB
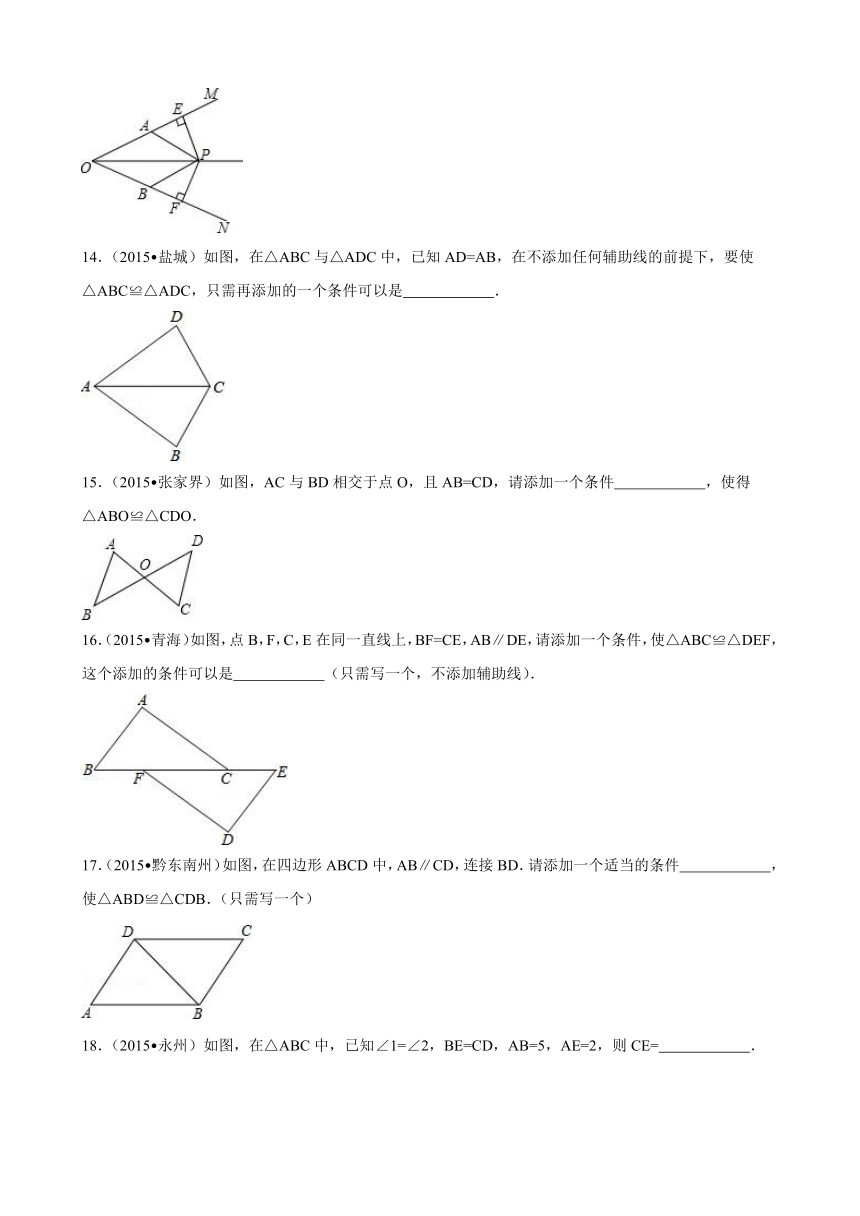
6.(2015 六盘水)如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
( http: / / www.21cnjy.com )
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
7.(2015 泰安)如图,AD是△ABC ( http: / / www.21cnjy.com )的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
( http: / / www.21cnjy.com )
A.4个 B.3个 C.2个 D.1个
8.(2015 柳州)如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
9.(2015 贵阳)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
( http: / / www.21cnjy.com )
A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE
10.(2015 宜昌)两组邻边分别相等的 ( http: / / www.21cnjy.com )四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,
其中正确的结论有( )
( http: / / www.21cnjy.com )
A.0个 B.1个 C.2个 D.3个
11.(2015 荆门)如 ( http: / / www.21cnjy.com )图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
12.(2015 齐齐哈尔)如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
13.(2015 南昌)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有 对全等三角形.
( http: / / www.21cnjy.com )
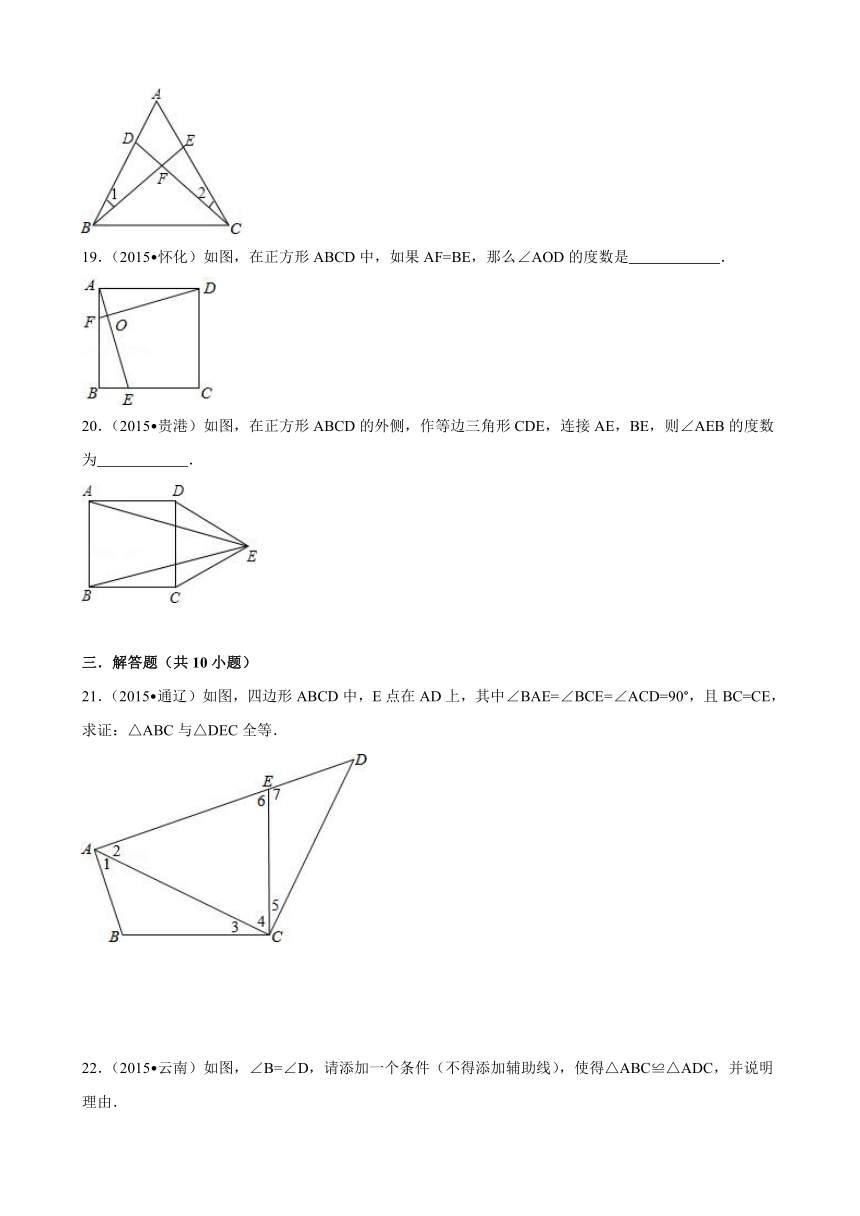
14.(2015 盐城)如图,在△AB ( http: / / www.21cnjy.com )C与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是 .
( http: / / www.21cnjy.com )
15.(2015 张家界)如图,AC与BD相交于点O,且AB=CD,请添加一个条件 ,使得△ABO≌△CDO.
( http: / / www.21cnjy.com )
16.(2015 青海)如图,点B ( http: / / www.21cnjy.com ),F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 (只需写一个,不添加辅助线).
( http: / / www.21cnjy.com )
17.(2015 黔东南州)如图, ( http: / / www.21cnjy.com )在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件 ,使△ABD≌△CDB.(只需写一个)
( http: / / www.21cnjy.com )
18.(2015 永州)如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .
( http: / / www.21cnjy.com )
19.(2015 怀化)如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是 .
( http: / / www.21cnjy.com )
20.(2015 贵港)如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为 .
( http: / / www.21cnjy.com )
三.解答题(共10小题)
21.(2015 通辽)如图,四边形ABCD ( http: / / www.21cnjy.com )中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
( http: / / www.21cnjy.com )
22.(2015 云南)如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
( http: / / www.21cnjy.com )
23.(2015 无锡)已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.
( http: / / www.21cnjy.com )
24.(2015 温州)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD.
(2)若AB=CF,∠B=30°,求∠D的度数.
( http: / / www.21cnjy.com )
25.(2015 泸州)如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
( http: / / www.21cnjy.com )
26.(2015 武汉)如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:
(1)△ABC≌△DEF;
(2)AB∥DE.
( http: / / www.21cnjy.com )
27.(2015 福州)如图,∠1=∠2,∠3=∠4,求证:AC=AD.
( http: / / www.21cnjy.com )
28.(2015 嘉兴)如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G,
(1)观察图形,写出图中所有与∠AED相等的角.
(2)选择图中与∠AED相等的任意一个角,并加以证明.
( http: / / www.21cnjy.com )
29.(2015 重庆)如 ( http: / / www.21cnjy.com )图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
( http: / / www.21cnjy.com )
30.(2015 恩施州)如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
( http: / / www.21cnjy.com )
参考答案
一.选择题(共12小题)
1. A. 2. A. 3. C 4. C. 5. D. 6. D. 7. A. 8. B.
9. B. 10. D 11. D. 12. D.
二.填空题(共8小题)
13. 3. 14. DC=BC或∠DAC=∠BAC 15.∠A=∠C.(答案不唯一)
16. AB=DE. 17. AB=CD. 18. 3. 19. 90°. 20. 30°.
三.解答题(共10小题)
21.解:∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5,∴∠3=∠5,
在△ACD中,∠ACD=90°,∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,∴∠1=∠D,
在△ABC和△DEC中,,∴△ABC≌△DEC(AAS).
22.解:添加∠BAC=∠DAC.理由如下:
在△ABC与△ADC中,,∴△ABC≌△ADC(AAS).
23.证明:(1)∵AB∥CD,∴∠AEC=∠ECD,∠BED=∠EDC,
∵CE=DE,∴∠ECD=∠EDC,∴∠AEC=∠BED;
(2)∵E是AB的中点,∴AE=BE,
在△AEC和△BED中,,∴△AEC≌△BED(SAS),∴AC=BD.
24.证明:(1)∵AB∥CD,∴∠B=∠C,
在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AB=CD;
(2)∵△ABE≌△CDF,∴AB=CD,BE=CF,
∵AB=CF,∠B=30°,∴AB=BE,∴△ABE是等腰三角形,
∴∠D=.
25.证明:∵∠1=∠2,∴∠CAB=∠DAE,
在△BAC和△DAE中,,∴△BAC≌△DAE(SAS),∴BC=DE.
26.证明:(1)∵AC⊥BC于点C,DF⊥EF于点F,
∴∠ACB=∠DFE=90°,
在△ABC和△DEF中,,∴△ABC≌△DEF(SAS);
(2)∵△ABC≌△DEF,∴∠B=∠DEF,
∴AB∥DE.
27.证明:∵∠3=∠4,∴∠ABC=∠ABD,
在△ABC和△ABD中,,∴△ABC≌△ABD(ASA),∴AC=AD.
28.解:(1)由图可知,∠DAG,∠AFB,∠CDE与∠AED相等;
(2)选择∠DAG=∠AED,证明如下:
∵正方形ABCD,∴∠DAB=∠B=90°,AD=AB,
∵AF=DE,
在△DAE与△ABF中,,∴△DAE≌△ABF(HL),∴∠ADE=∠BAF,
∵∠DAG+∠BAF=90°,∠GDA+∠AED=90°,∴∠DAG=∠AED.
29.证明:∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE,
在△ABD与△FEC中,
,
∴△ABD≌△FEC(SAS),
∴∠ADB=∠FCE.
30.(1)证明:∵四边形ABCD、BEFG均为正方形,
∴AB=CB,∠ABC=∠GBE=90°,BG=BE,
∴∠ABG=∠CBE,
在△ABG和△CBE中,,
∴△ABG≌△CBE(SAS),
∴AG=CE;
(2)证明:如图所示:∵△ABG≌△CBE,
∴∠BAG=∠BCE,
∵∠ABC=90°,
∴∠BAG+∠AMB=90°,
∵∠AMB=∠CMN,
∴∠BCE+∠CMN=90°,
∴∠CNM=90°,
∴AG⊥CE.
( http: / / www.21cnjy.com )
一.选择题(共12小题)
1.(2015 百色)下列图形中具有稳定性的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
2.(2015 莆田)如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
( http: / / www.21cnjy.com )
A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC
3.(2015 宜昌)如图,在方格纸中, ( http: / / www.21cnjy.com )以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
4.(2015 宁波)如图, ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
( http: / / www.21cnjy.com )
A.BE=DF B.BF=DE C.AE=CF D.∠1=∠2
5.(2015 海南)如图,下列条件中,不能证明△ABC≌△DCB的是( )
( http: / / www.21cnjy.com )
A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D D.AB=DC,∠DBC=∠ACB
6.(2015 六盘水)如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
( http: / / www.21cnjy.com )
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
7.(2015 泰安)如图,AD是△ABC ( http: / / www.21cnjy.com )的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
( http: / / www.21cnjy.com )
A.4个 B.3个 C.2个 D.1个
8.(2015 柳州)如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
9.(2015 贵阳)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
( http: / / www.21cnjy.com )
A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE
10.(2015 宜昌)两组邻边分别相等的 ( http: / / www.21cnjy.com )四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,
其中正确的结论有( )
( http: / / www.21cnjy.com )
A.0个 B.1个 C.2个 D.3个
11.(2015 荆门)如 ( http: / / www.21cnjy.com )图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
12.(2015 齐齐哈尔)如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
13.(2015 南昌)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有 对全等三角形.
( http: / / www.21cnjy.com )
14.(2015 盐城)如图,在△AB ( http: / / www.21cnjy.com )C与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是 .
( http: / / www.21cnjy.com )
15.(2015 张家界)如图,AC与BD相交于点O,且AB=CD,请添加一个条件 ,使得△ABO≌△CDO.
( http: / / www.21cnjy.com )
16.(2015 青海)如图,点B ( http: / / www.21cnjy.com ),F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 (只需写一个,不添加辅助线).
( http: / / www.21cnjy.com )
17.(2015 黔东南州)如图, ( http: / / www.21cnjy.com )在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件 ,使△ABD≌△CDB.(只需写一个)
( http: / / www.21cnjy.com )
18.(2015 永州)如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .
( http: / / www.21cnjy.com )
19.(2015 怀化)如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是 .
( http: / / www.21cnjy.com )
20.(2015 贵港)如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为 .
( http: / / www.21cnjy.com )
三.解答题(共10小题)
21.(2015 通辽)如图,四边形ABCD ( http: / / www.21cnjy.com )中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
( http: / / www.21cnjy.com )
22.(2015 云南)如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
( http: / / www.21cnjy.com )
23.(2015 无锡)已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.
( http: / / www.21cnjy.com )
24.(2015 温州)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD.
(2)若AB=CF,∠B=30°,求∠D的度数.
( http: / / www.21cnjy.com )
25.(2015 泸州)如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
( http: / / www.21cnjy.com )
26.(2015 武汉)如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:
(1)△ABC≌△DEF;
(2)AB∥DE.
( http: / / www.21cnjy.com )
27.(2015 福州)如图,∠1=∠2,∠3=∠4,求证:AC=AD.
( http: / / www.21cnjy.com )
28.(2015 嘉兴)如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G,
(1)观察图形,写出图中所有与∠AED相等的角.
(2)选择图中与∠AED相等的任意一个角,并加以证明.
( http: / / www.21cnjy.com )
29.(2015 重庆)如 ( http: / / www.21cnjy.com )图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
( http: / / www.21cnjy.com )
30.(2015 恩施州)如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
( http: / / www.21cnjy.com )
参考答案
一.选择题(共12小题)
1. A. 2. A. 3. C 4. C. 5. D. 6. D. 7. A. 8. B.
9. B. 10. D 11. D. 12. D.
二.填空题(共8小题)
13. 3. 14. DC=BC或∠DAC=∠BAC 15.∠A=∠C.(答案不唯一)
16. AB=DE. 17. AB=CD. 18. 3. 19. 90°. 20. 30°.
三.解答题(共10小题)
21.解:∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5,∴∠3=∠5,
在△ACD中,∠ACD=90°,∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,∴∠1=∠D,
在△ABC和△DEC中,,∴△ABC≌△DEC(AAS).
22.解:添加∠BAC=∠DAC.理由如下:
在△ABC与△ADC中,,∴△ABC≌△ADC(AAS).
23.证明:(1)∵AB∥CD,∴∠AEC=∠ECD,∠BED=∠EDC,
∵CE=DE,∴∠ECD=∠EDC,∴∠AEC=∠BED;
(2)∵E是AB的中点,∴AE=BE,
在△AEC和△BED中,,∴△AEC≌△BED(SAS),∴AC=BD.
24.证明:(1)∵AB∥CD,∴∠B=∠C,
在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AB=CD;
(2)∵△ABE≌△CDF,∴AB=CD,BE=CF,
∵AB=CF,∠B=30°,∴AB=BE,∴△ABE是等腰三角形,
∴∠D=.
25.证明:∵∠1=∠2,∴∠CAB=∠DAE,
在△BAC和△DAE中,,∴△BAC≌△DAE(SAS),∴BC=DE.
26.证明:(1)∵AC⊥BC于点C,DF⊥EF于点F,
∴∠ACB=∠DFE=90°,
在△ABC和△DEF中,,∴△ABC≌△DEF(SAS);
(2)∵△ABC≌△DEF,∴∠B=∠DEF,
∴AB∥DE.
27.证明:∵∠3=∠4,∴∠ABC=∠ABD,
在△ABC和△ABD中,,∴△ABC≌△ABD(ASA),∴AC=AD.
28.解:(1)由图可知,∠DAG,∠AFB,∠CDE与∠AED相等;
(2)选择∠DAG=∠AED,证明如下:
∵正方形ABCD,∴∠DAB=∠B=90°,AD=AB,
∵AF=DE,
在△DAE与△ABF中,,∴△DAE≌△ABF(HL),∴∠ADE=∠BAF,
∵∠DAG+∠BAF=90°,∠GDA+∠AED=90°,∴∠DAG=∠AED.
29.证明:∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE,
在△ABD与△FEC中,
,
∴△ABD≌△FEC(SAS),
∴∠ADB=∠FCE.
30.(1)证明:∵四边形ABCD、BEFG均为正方形,
∴AB=CB,∠ABC=∠GBE=90°,BG=BE,
∴∠ABG=∠CBE,
在△ABG和△CBE中,,
∴△ABG≌△CBE(SAS),
∴AG=CE;
(2)证明:如图所示:∵△ABG≌△CBE,
∴∠BAG=∠BCE,
∵∠ABC=90°,
∴∠BAG+∠AMB=90°,
∵∠AMB=∠CMN,
∴∠BCE+∠CMN=90°,
∴∠CNM=90°,
∴AG⊥CE.
( http: / / www.21cnjy.com )
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
