数学:16.3《加法原理》课件(沪教版高三上)
文档属性
| 名称 | 数学:16.3《加法原理》课件(沪教版高三上) |

|
|
| 格式 | rar | ||
| 文件大小 | 583.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-04 13:51:00 | ||
图片预览









文档简介
课件33张PPT。加法原理 例1 学校组织读书活动,要求每个同学读一本书.小明到图书馆借书时,图书馆有不同的外语书150本,不同的科技书200本,不同的小说100本.那么,小明借一本书可以有多少种不同的选法?分析: 在这个问题中,小明选一本书有三类
方法.即要么选外语书,要么选科技书,
要么选小说.所以,是应用加法原理的问题.
解:小明借一本书共有:
150+200+100=450(种)
不同的选法.例2 一个口袋内装有3个小球,另一个
口袋内装有8个小球,所有这些小
球颜色各不相同.问:
①从两个口袋内任取一个小球,有多少
种不同的取法?
②从两个口袋内各取一个小球,有多少
种不同的取法?分析 ①从两个口袋中只需取一个小
球,则这个小球要么从第一个口
袋中取,要么从第二个口袋中
取,共有两大类方法.所以是加
法原理的问题. ②要从两个口袋中各取一个小球,
则可看成先从第一个口袋中取一
个,再从第二个口袋中取一个,
分两步完成,是乘法原理的问题.解:①从两个口袋中任取一个小球共有
3+8=11(种),
不同的取法.
②从两个口袋中各取一个小球共有
3×8=24(种)
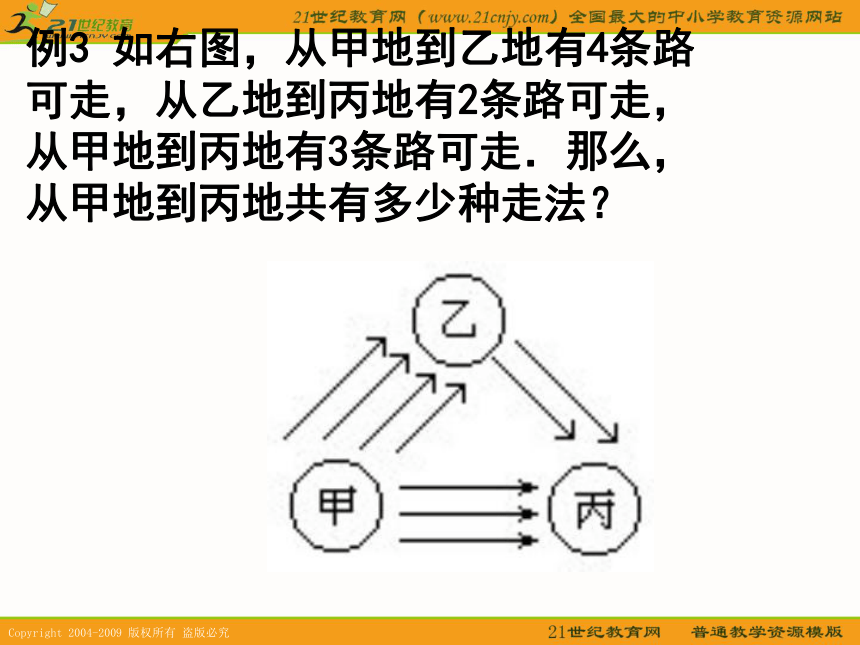
不同的取法.例3 如右图,从甲地到乙地有4条路可走,从乙地到丙地有2条路可走,从甲地到丙地有3条路可走.那么,从甲地到丙地共有多少种走法?分析 从甲地到丙地共有两大类不同的走法.
第一类,由甲地途经乙地到丙地.这时,要分两步走,第一步从甲地到乙地,有4种走法;第二步从乙地到丙地共2种走法,所以由乘法原理,这时共有4×2=8种不同的走法.
第二类,由甲地直接到丙地,由条件知,有3种不同的走法.
解:由加法原理知,由甲地到丙地共有:
4×2+3=11(种)
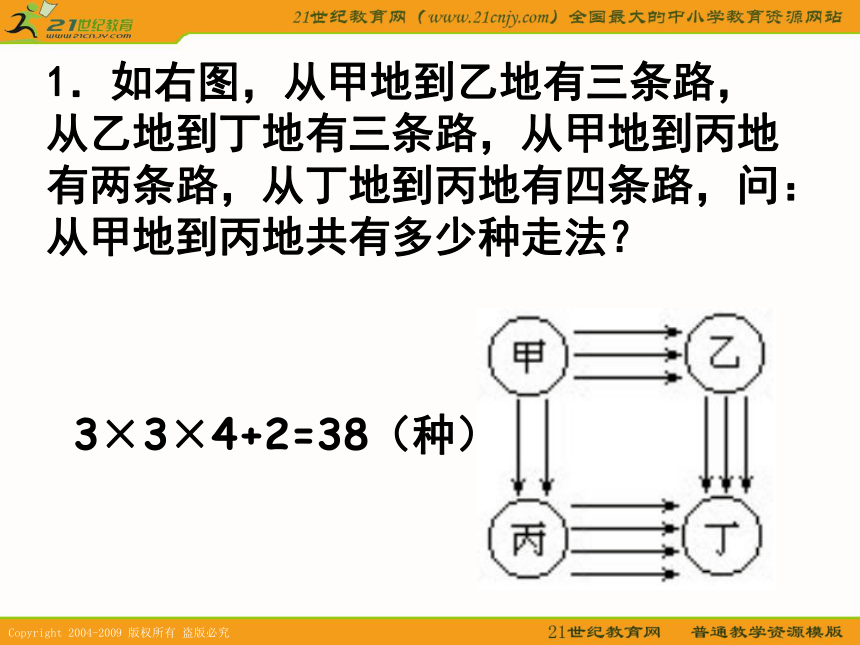
不同的走法.1.如右图,从甲地到乙地有三条路,从乙地到丁地有三条路,从甲地到丙地有两条路,从丁地到丙地有四条路,问:从甲地到丙地共有多少种走法?3×3×4+2=38(种) 2.书架上有6本不同的画报和7本不同的书,从中最多拿两本(不能不拿),有多少种不同的拿法?6+7+15+21+6×7=91(种).
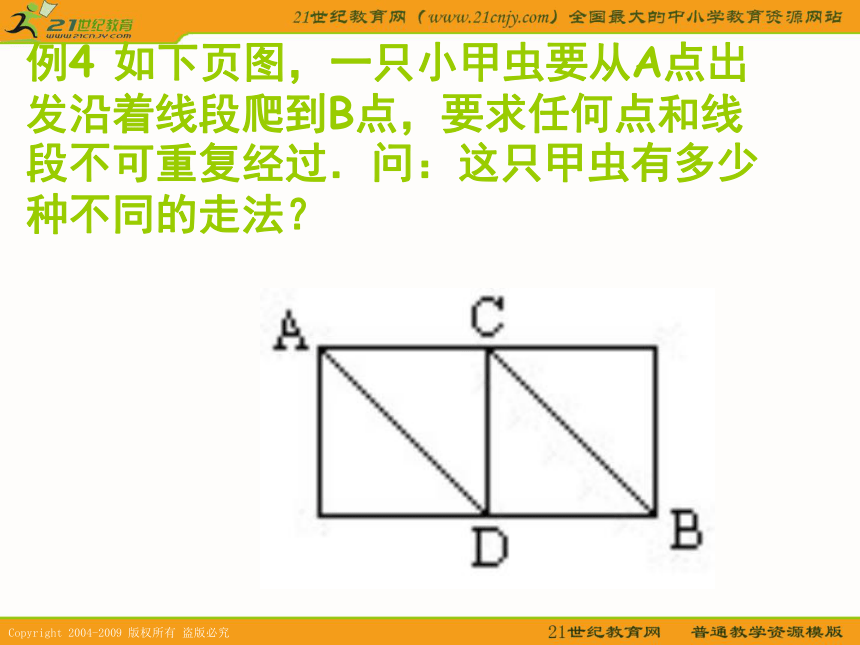
提示:拿两本的情况分为2本画报或2本书或一本画报一本书.3.如下图中,沿线段从点A走最短 的路线到B,各有多少种走法?(1)6; (2)10; (3)20; (4)35 例4 如下页图,一只小甲虫要从A点出发沿着线段爬到B点,要求任何点和线段不可重复经过.问:这只甲虫有多少种不同的走法?分析 从A点到B点有两类走法,一类是从A点先经过C点到B点,一类是从A点先经过D点到B点.两类中的每一种具体走法都要分两步完成,所以每一类中,都要用乘法原理,而最后计算从A到B的全部走法时,只要用加法原理求和即可. 解:从A点先经过C到B点共有:
1×3=3(种)
不同的走法.
从A点先经过D到B点共有:
2×3=6(种)
不同的走法.
所以,从A点到B点共有:
3+6=9(种)
不同的走法.例5 有两个相同的正方体,每个正方体的六个面上分别标有数字1、2、3、4、5、6.将两个正方体放到桌面上,向上的一面数字之和为偶数的有多少种情形?分析 要使两个数字之和为偶数,只要这两个数字的奇偶性相同,即这两个数字要么同为奇数,要么同为偶数,所以,要分两大类来考虑.
第一类,两个数字同为奇数.由于放两个正方体可认为是一个一个地放.放第一个正方体时,出现奇数有三种可能,即1,3,5;放第二个正方体,出现奇数也有三种可能,由乘法原理,这时共有3×3=9种不同的情形.
第二类,两个数字同为偶数,类似第一类的讨论方法,也有3×3=9种不同情形.
最后再由加法原理即可求解.例6 从1到500的所有自然数中,不含有数字4的自然数有多少个?分析 从1到500的所有自然数可分为三大类,即一位数,两位数,三位数.
一位数中,不含4的有8个,它们是1、2、3、5、6、7、8、9;
两位数中,不含4的可以这样考虑:十位上,不含4的有1、2、3、5、6、7、8、9这八种情况.个位上,不含4的有0、1、2、3、5、6、7、8、9这九种情况,要确定一个两位数,可以先取十位数,再取个位数,应用乘法原理,这时共
有 8×9=72个数不含4.三位数中,小于500并且不含数字4的可以这样考虑:百位上,不含4的有1、2、3、这三种情况.十位上,不含4的有0、1、2、3、5、6、7、8、9这九种情况,个位上,不含4的也有九种情况.要确定一个三位数,可以先取百位数,再取十位数,最后取个位数,应用乘法原理,这时共有3×9×9=243个三位数.由于500也是一个不含4的三位数.所以,1~500中,不含4的三位数共有3×9×9+1=244个. 解:在1~500中,不含4的一位数有8个;不含4的两位数有8×9=72个;不含4的三位数有3×9×9+1=244个,由加法原理,在1~500中,共有:
8+8×9+3×9×9+1=324(个)
不含4的自然数.4.在1~1000的自然数中,一共有多少个数字0?9+180+3=192(个). 5.在1~500的自然数中,不含数字0和1的数有多少个?8+8×8+3×8×8=264(个). 6.十把钥匙开十把锁,但不知道哪把
钥匙开哪把锁,问:最多试开多少次,
就能把锁和钥匙配起来?
9+8+7+6+5+4+3+2+1=45(次)
7、有五顶不同的帽子,两件不同的上衣,三条不同的裤子。从中取出一顶帽子、一件上衣、一条裤子配成一套装束。问:有多少种不同的装束?5×2×3=30(种)例7 如下页左图,要从A点沿线段走
到B,要求每一步都是向右、向
上或者向斜上方.问有多少种
不同的走法?分析 观察下页左图,注意到,从A到B要一
直向右、向上,那么,经过下页右图
中C、D、E、F四点中的某一点的路线
一定不再经过其他的点.也就是说从
A到B点的路线共分为四类,它们是分
别经过C、D、E、F的路线. 第一类,经过C的路线,分为两步,从A到C再从C到B,从A到C有2条路可走,从C到B也有两条路可走,由乘法原理,从A经C到B共有2×2=4条不同的路线.
第二类,经过D点的路线,分为两步,从A到D有4条路,从D到B有4条路,由乘法原理,从A经D到B共有4×4=16种不同的走法. 第三类,经过E点的路线,分为两步,从A到E再从E到B,观察发现.各有一条路.所以,从A经E到B共有1种走法.
第四类,经过F点的路线,从A经F到B只有一种走法.
最后由加法原理即可求解.
解:如上右图,从A到B共有下面的走法:
从A经C到B共有2×2=4种走法;
从A经D到B共有4×4=16种走法;
从A经E到B共有1种走法;
从A经F到B共有1种走法.
所以,从A到B共有:
4+16+1+1=22
种不同的走法.
?例8 甲组有6人,乙组有8人,丙组
有9人。从三个组中各选一人
参加会议,共有多少种不同
选法?6×8×9=432(种)例9从甲地到乙地有4条不同的路,从乙地到丙地有6条不同的路。那么从甲地经乙地到丙地共有多少不同的路?4×6=24(条)8、用一张10元、一张5元、一张
2元、一张1元,可组成多少
种不同的币值?4+6+4+1=15(种)9、从5幅国画,3幅油画,2幅水彩画中选取两幅不同类型的画布置教室,问有几种选法?解:依加法原理,选取两幅不同类型
的画布置教室的选法有:
15+10+6=31种 10、一个口袋内装有5个小球,另一个口袋内装有9个小球,所有这些小球颜色各不相同.
问:①从两个口袋内任取一个小球,有多少种不同的取法?
②从两个口袋内各取一个小球,有多少种不同的取法?9+5=14(种)5×9=45(种)
方法.即要么选外语书,要么选科技书,
要么选小说.所以,是应用加法原理的问题.
解:小明借一本书共有:
150+200+100=450(种)
不同的选法.例2 一个口袋内装有3个小球,另一个
口袋内装有8个小球,所有这些小
球颜色各不相同.问:
①从两个口袋内任取一个小球,有多少
种不同的取法?
②从两个口袋内各取一个小球,有多少
种不同的取法?分析 ①从两个口袋中只需取一个小
球,则这个小球要么从第一个口
袋中取,要么从第二个口袋中
取,共有两大类方法.所以是加
法原理的问题. ②要从两个口袋中各取一个小球,
则可看成先从第一个口袋中取一
个,再从第二个口袋中取一个,
分两步完成,是乘法原理的问题.解:①从两个口袋中任取一个小球共有
3+8=11(种),
不同的取法.
②从两个口袋中各取一个小球共有
3×8=24(种)
不同的取法.例3 如右图,从甲地到乙地有4条路可走,从乙地到丙地有2条路可走,从甲地到丙地有3条路可走.那么,从甲地到丙地共有多少种走法?分析 从甲地到丙地共有两大类不同的走法.
第一类,由甲地途经乙地到丙地.这时,要分两步走,第一步从甲地到乙地,有4种走法;第二步从乙地到丙地共2种走法,所以由乘法原理,这时共有4×2=8种不同的走法.
第二类,由甲地直接到丙地,由条件知,有3种不同的走法.
解:由加法原理知,由甲地到丙地共有:
4×2+3=11(种)
不同的走法.1.如右图,从甲地到乙地有三条路,从乙地到丁地有三条路,从甲地到丙地有两条路,从丁地到丙地有四条路,问:从甲地到丙地共有多少种走法?3×3×4+2=38(种) 2.书架上有6本不同的画报和7本不同的书,从中最多拿两本(不能不拿),有多少种不同的拿法?6+7+15+21+6×7=91(种).
提示:拿两本的情况分为2本画报或2本书或一本画报一本书.3.如下图中,沿线段从点A走最短 的路线到B,各有多少种走法?(1)6; (2)10; (3)20; (4)35 例4 如下页图,一只小甲虫要从A点出发沿着线段爬到B点,要求任何点和线段不可重复经过.问:这只甲虫有多少种不同的走法?分析 从A点到B点有两类走法,一类是从A点先经过C点到B点,一类是从A点先经过D点到B点.两类中的每一种具体走法都要分两步完成,所以每一类中,都要用乘法原理,而最后计算从A到B的全部走法时,只要用加法原理求和即可. 解:从A点先经过C到B点共有:
1×3=3(种)
不同的走法.
从A点先经过D到B点共有:
2×3=6(种)
不同的走法.
所以,从A点到B点共有:
3+6=9(种)
不同的走法.例5 有两个相同的正方体,每个正方体的六个面上分别标有数字1、2、3、4、5、6.将两个正方体放到桌面上,向上的一面数字之和为偶数的有多少种情形?分析 要使两个数字之和为偶数,只要这两个数字的奇偶性相同,即这两个数字要么同为奇数,要么同为偶数,所以,要分两大类来考虑.
第一类,两个数字同为奇数.由于放两个正方体可认为是一个一个地放.放第一个正方体时,出现奇数有三种可能,即1,3,5;放第二个正方体,出现奇数也有三种可能,由乘法原理,这时共有3×3=9种不同的情形.
第二类,两个数字同为偶数,类似第一类的讨论方法,也有3×3=9种不同情形.
最后再由加法原理即可求解.例6 从1到500的所有自然数中,不含有数字4的自然数有多少个?分析 从1到500的所有自然数可分为三大类,即一位数,两位数,三位数.
一位数中,不含4的有8个,它们是1、2、3、5、6、7、8、9;
两位数中,不含4的可以这样考虑:十位上,不含4的有1、2、3、5、6、7、8、9这八种情况.个位上,不含4的有0、1、2、3、5、6、7、8、9这九种情况,要确定一个两位数,可以先取十位数,再取个位数,应用乘法原理,这时共
有 8×9=72个数不含4.三位数中,小于500并且不含数字4的可以这样考虑:百位上,不含4的有1、2、3、这三种情况.十位上,不含4的有0、1、2、3、5、6、7、8、9这九种情况,个位上,不含4的也有九种情况.要确定一个三位数,可以先取百位数,再取十位数,最后取个位数,应用乘法原理,这时共有3×9×9=243个三位数.由于500也是一个不含4的三位数.所以,1~500中,不含4的三位数共有3×9×9+1=244个. 解:在1~500中,不含4的一位数有8个;不含4的两位数有8×9=72个;不含4的三位数有3×9×9+1=244个,由加法原理,在1~500中,共有:
8+8×9+3×9×9+1=324(个)
不含4的自然数.4.在1~1000的自然数中,一共有多少个数字0?9+180+3=192(个). 5.在1~500的自然数中,不含数字0和1的数有多少个?8+8×8+3×8×8=264(个). 6.十把钥匙开十把锁,但不知道哪把
钥匙开哪把锁,问:最多试开多少次,
就能把锁和钥匙配起来?
9+8+7+6+5+4+3+2+1=45(次)
7、有五顶不同的帽子,两件不同的上衣,三条不同的裤子。从中取出一顶帽子、一件上衣、一条裤子配成一套装束。问:有多少种不同的装束?5×2×3=30(种)例7 如下页左图,要从A点沿线段走
到B,要求每一步都是向右、向
上或者向斜上方.问有多少种
不同的走法?分析 观察下页左图,注意到,从A到B要一
直向右、向上,那么,经过下页右图
中C、D、E、F四点中的某一点的路线
一定不再经过其他的点.也就是说从
A到B点的路线共分为四类,它们是分
别经过C、D、E、F的路线. 第一类,经过C的路线,分为两步,从A到C再从C到B,从A到C有2条路可走,从C到B也有两条路可走,由乘法原理,从A经C到B共有2×2=4条不同的路线.
第二类,经过D点的路线,分为两步,从A到D有4条路,从D到B有4条路,由乘法原理,从A经D到B共有4×4=16种不同的走法. 第三类,经过E点的路线,分为两步,从A到E再从E到B,观察发现.各有一条路.所以,从A经E到B共有1种走法.
第四类,经过F点的路线,从A经F到B只有一种走法.
最后由加法原理即可求解.
解:如上右图,从A到B共有下面的走法:
从A经C到B共有2×2=4种走法;
从A经D到B共有4×4=16种走法;
从A经E到B共有1种走法;
从A经F到B共有1种走法.
所以,从A到B共有:
4+16+1+1=22
种不同的走法.
?例8 甲组有6人,乙组有8人,丙组
有9人。从三个组中各选一人
参加会议,共有多少种不同
选法?6×8×9=432(种)例9从甲地到乙地有4条不同的路,从乙地到丙地有6条不同的路。那么从甲地经乙地到丙地共有多少不同的路?4×6=24(条)8、用一张10元、一张5元、一张
2元、一张1元,可组成多少
种不同的币值?4+6+4+1=15(种)9、从5幅国画,3幅油画,2幅水彩画中选取两幅不同类型的画布置教室,问有几种选法?解:依加法原理,选取两幅不同类型
的画布置教室的选法有:
15+10+6=31种 10、一个口袋内装有5个小球,另一个口袋内装有9个小球,所有这些小球颜色各不相同.
问:①从两个口袋内任取一个小球,有多少种不同的取法?
②从两个口袋内各取一个小球,有多少种不同的取法?9+5=14(种)5×9=45(种)
