3.1图形的平移培优练习（含解析）

3.1图形的平移培优练习北师大版2024—2025学年春季八年级下册
一、选择题
1．本届亚冬会的吉祥物是一对可爱的东北虎“滨滨”和“妮妮”．“滨滨”和“妮妮”的原型是2023年9月出生于黑龙江东北虎林园的两只可爱的小东北虎，“滨滨”名字取自“哈尔滨”，“妮妮”取自“您”的读音，两个名字寓意“哈尔滨欢迎您”．如图，通过平移吉祥物，可以得到的图形是（　　）
A． B． C． D．
2．下面所示的图案中，可以看成是由图案自身的一部分经过平移得到的是（　　）
A． B． C． D．
3．如图，将△ABC向右平移得到△DEF，且点B，E，C，F在同一条直线上，若EC＝2，BF＝8，则AD的长为（　　）
A．2 B．3 C．5 D．6
4．如图，将△ABC沿CB方向平移1个单位长度得到△DEF，已知CB＝3，则CE的长为（　　）
A．3 B．4 C．5 D．6
5．如图，将三角形ABC沿BC方向平移到三角形DEF的位置，已知点A，D之间的距离为1，BF＝4，则EC的长是（　　）
A．1 B．2 C．3 D．4
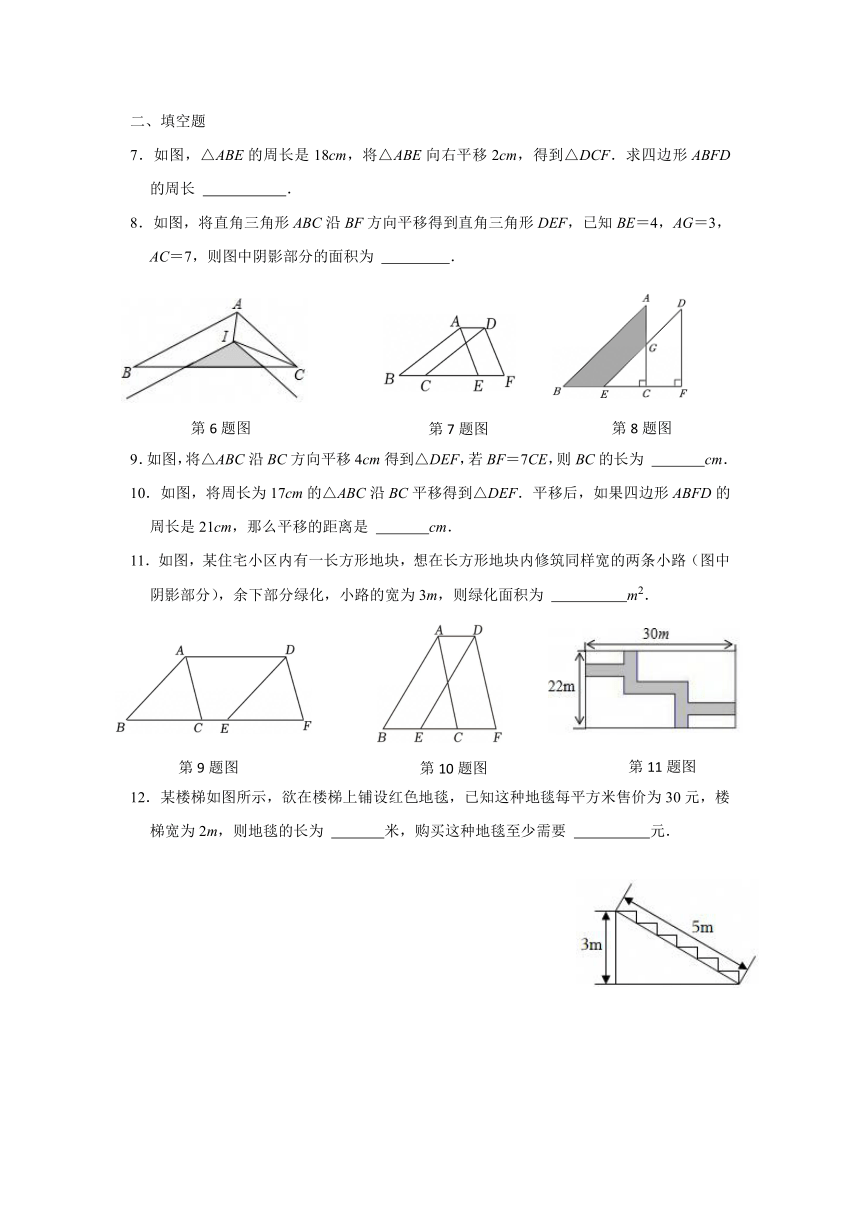
6．如图，在△ABC中，AB＝5，AC＝4，BC＝8，AI平分∠BAC，CI平分∠ACB，将∠BAC平移，使其顶点与点I重合，则图中阴影部分的周长为（　　）
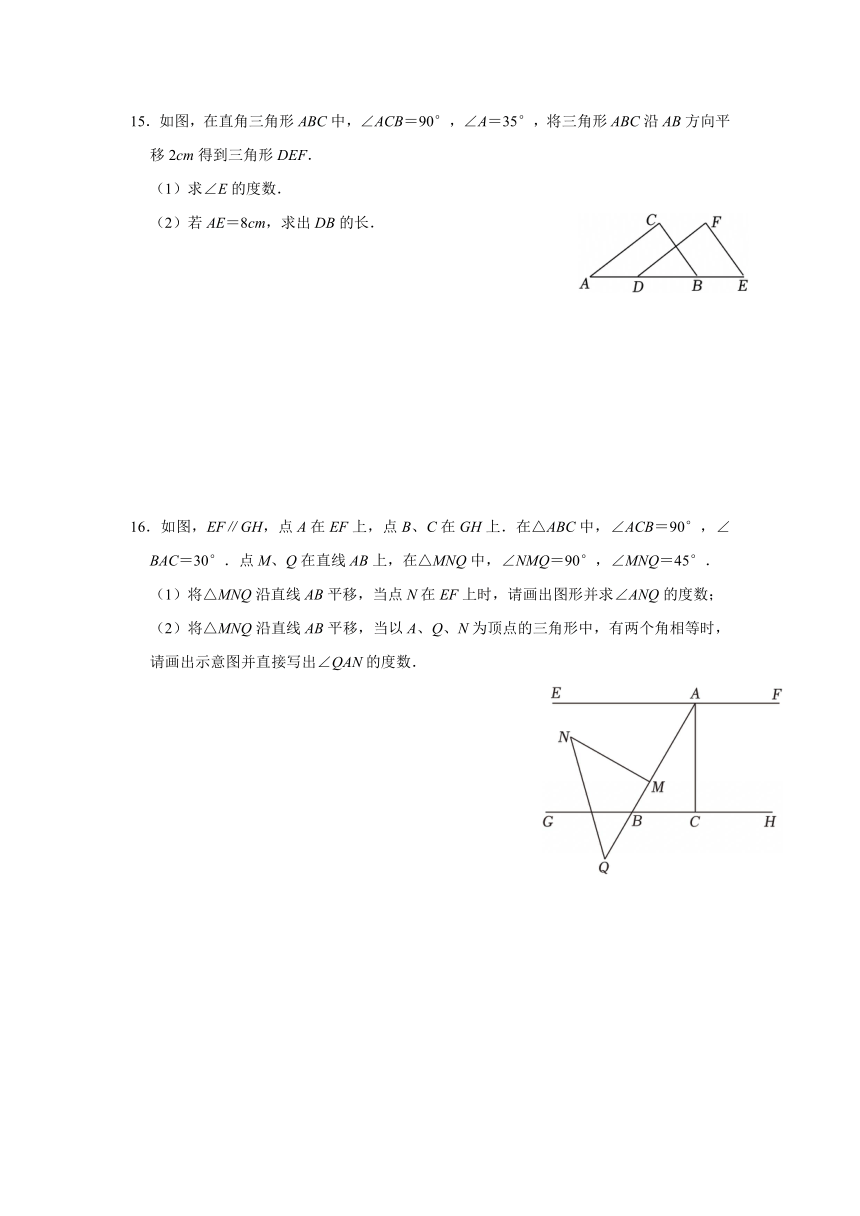
A．8 B．9 C．10 D．10.5
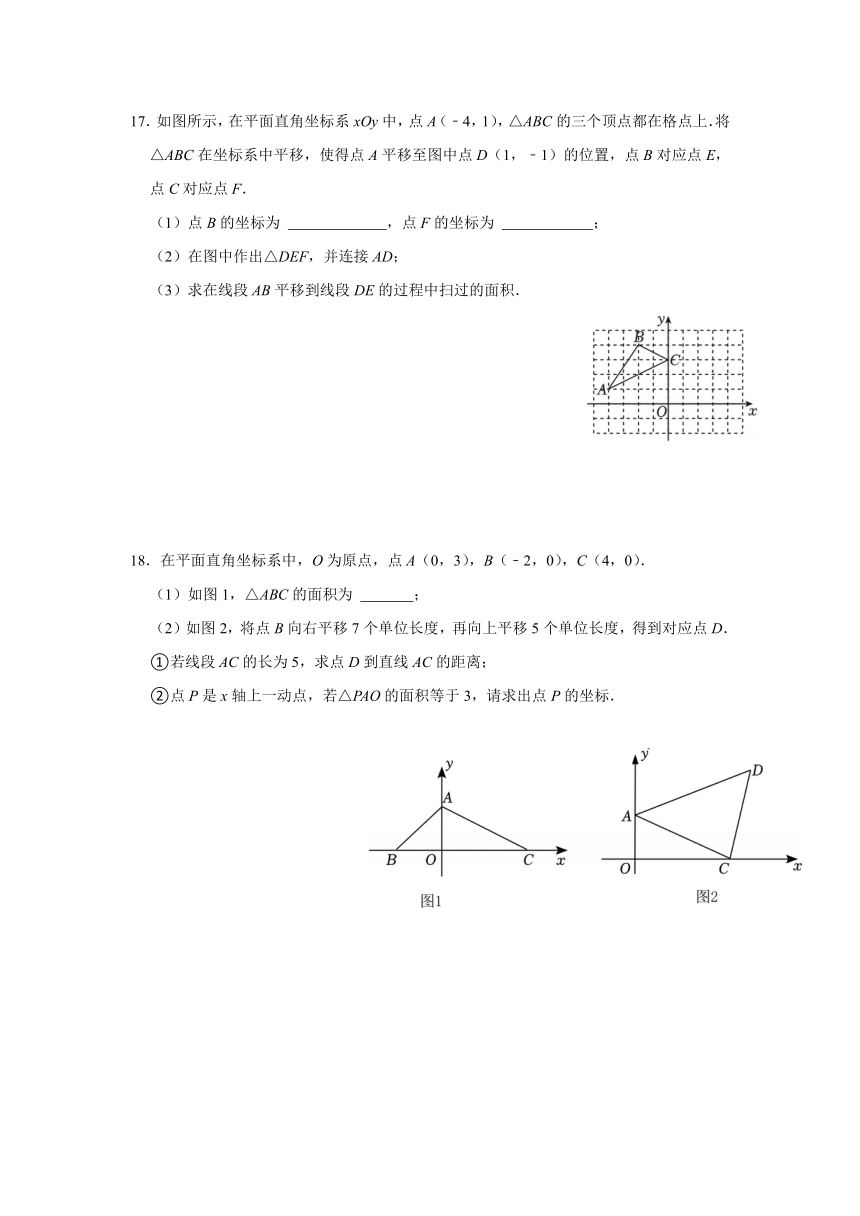
二、填空题
7．如图，△ABE的周长是18cm，将△ABE向右平移2cm，得到△DCF．求四边形ABFD的周长 　 　．
8．如图，将直角三角形ABC沿BF方向平移得到直角三角形DEF，已知BE＝4，AG＝3，AC＝7，则图中阴影部分的面积为 　 　．
9．如图，将△ABC沿BC方向平移4cm得到△DEF，若BF＝7CE，则BC的长为 　 　cm．
10．如图，将周长为17cm的△ABC沿BC平移得到△DEF．平移后，如果四边形ABFD的周长是21cm，那么平移的距离是 　 　cm．
11．如图，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条小路（图中阴影部分），余下部分绿化，小路的宽为3m，则绿化面积为 　 　m2．
12．某楼梯如图所示，欲在楼梯上铺设红色地毯，已知这种地毯每平方米售价为30元，楼梯宽为2m，则地毯的长为 　 　米，购买这种地毯至少需要 　 　元．
三、解答题
13．在平面直角坐标系xOy中，已知点A（4，1），B（1，﹣2），将线段AB向左平移4个单位，再向上平移1个单位，得到线段A1B1．
（1）在图中画出线段A1B1，并直接写出点A1、B1的坐标；
（2）点M在y轴上，若三角形A1B1M的面积为3，求点M的坐标．
14．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣1，2），B（﹣3，1），C（0，﹣1）．
（1）将△ABC先向右沿平移3个单位长度，再向下平移1个单位长度得到△A1B1C1，请在如图中作出平移后的△A1B1C1．
（2）点A1的坐标为 　 　，△A1B1C1的面积为 　 　．
15．如图，在直角三角形ABC中，∠ACB＝90°，∠A＝35°，将三角形ABC沿AB方向平移2cm得到三角形DEF．
（1）求∠E的度数．
（2）若AE＝8cm，求出DB的长．
16．如图，EF∥GH，点A在EF上，点B、C在GH上．在△ABC中，∠ACB＝90°，∠BAC＝30°．点M、Q在直线AB上，在△MNQ中，∠NMQ＝90°，∠MNQ＝45°．
（1）将△MNQ沿直线AB平移，当点N在EF上时，请画出图形并求∠ANQ的度数；
（2）将△MNQ沿直线AB平移，当以A、Q、N为顶点的三角形中，有两个角相等时，请画出示意图并直接写出∠QAN的度数．
17．如图所示，在平面直角坐标系xOy中，点A（﹣4，1），△ABC的三个顶点都在格点上．将△ABC在坐标系中平移，使得点A平移至图中点D（1，﹣1）的位置，点B对应点E，点C对应点F．
（1）点B的坐标为 　 　，点F的坐标为 　 　；
（2）在图中作出△DEF，并连接AD；
（3）求在线段AB平移到线段DE的过程中扫过的面积．
18．在平面直角坐标系中，O为原点，点A（0，3），B（﹣2，0），C（4，0）．
（1）如图1，△ABC的面积为 　 　；
（2）如图2，将点B向右平移7个单位长度，再向上平移5个单位长度，得到对应点D．
①若线段AC的长为5，求点D到直线AC的距离；
②点P是x轴上一动点，若△PAO的面积等于3，请求出点P的坐标．
参考答案
1．【解答】解：根据平移的定义，平移前后的图形形状、大小完全一样，仅位置不一样，那么D符合题意．
故选：D．
2．【解答】解：A、是一个对称图形，不能由平移得到，故此选项不合题意；
B、是一个对称图形，不能由平移得到，故此选项不合题意；
C、是一个对称图形，不能由平移得到，故此选项不合题意；
D、图案自身的一部分沿着直线运动而得到，是平移，故此选项符合题意．
故选：D．
3．【解答】解：∵△DEF是由△ABC向右平移得到，
∴BC＝EF，AD＝BE，
∴BE＝CF＝（8﹣2）÷2＝3，
∴AD＝BE＝3．
故选：B．
4．【解答】解：∵将△ABC沿CB方向平移1个单位长度得到△DEF，
∴BE＝CD＝1，
∵CB＝3，
∴CE＝BE+BC＝4，
故选：B．
5．【解答】解：∵三角形ABC沿水平方向向右平移到三角形DEF，AD＝1，
∴BE＝CF＝AD＝1，
∵BF＝4，
∴EC＝BF﹣BE﹣CF＝4﹣1﹣1＝2．
故选：B．
6．【解答】解：如图，连接BI，
∵AI平分∠BAC，CI平分∠ACB，
∴BI平分∠ABC，
由平移的性质可知，MI∥AB，NI∥AC，
∴∠ABI＝∠MBI＝∠MIB，∠ACI＝∠NCI＝∠NIC，
∴MI＝MB，NI＝NC，
∴阴影部分的周长为MI+MN+NI＝MB+MN+NC＝BC＝8，
故选：A．
7．【解答】解：由平移可知，
AD＝EF＝2cm，DF＝AE，
所以四边形ABFD的周长为：AB+BF+DF+AD＝AB+BE+EF+AE+AD＝AB+BE+AE+4（cm）．
又因为△ABE的周长是18cm，
即AB+BE+AE＝18cm，
所以四边形ABFD的周长为：18+4＝22（cm）．
故答案为：22cm．
8．【解答】解：由平移的性质得，S△DEF＝S△ACB，DF＝AC＝7，BE＝CF＝4，
∴阴影部分的面积＝S梯形CFDG，
∵AG＝3，AC＝7，
∴GC＝AC﹣AG＝7﹣3＝4，
∴，
∴阴影部分的面积为22．
故答案为：22．
9．【解答】解：由平移可得，BE＝CF＝AD＝4cm，
∵BF＝BE+EF＝4+（CF﹣CE）＝4+4﹣CE＝7CE，
∴CE＝1cm，
∴BC＝BE﹣CE＝4﹣1＝3（cm），
故答案为：3．
10．【解答】解：∵△ABC沿BC平移得到△DEF，
∴AD＝BE，△ABC≌△DEF，
∴AB＝DE，
∵△ABC的周长为17cm，
∴△DEF的周长为17cm，
∵四边形ABFD的周长是21cm，
∴2AD+17＝21，
解得DE＝2，
故答案为：2．
11．【解答】解：根据题意，得（30﹣3）×（22﹣3）＝513（m2），
故答案为：513．
12．【解答】解：已知直角三角形的一条直角边是3m，斜边是5m，
根据勾股定理得到：水平的直角边是4（m），
地毯水平的部分的和是水平边的长，竖直的部分的和是竖直边的长，
则购买这种地毯的长是3+4＝7（m），
则面积是7×2＝14（m2）．
价格是14×30＝420（元）．
故答案为：7，420．
13．【解答】解：（1）如图，线段A1B1即为所求．
由图可得，A1（0，2），B1（﹣3，﹣1）．
（2）设点M的坐标为（0，m），
∵三角形A1B1M的面积为3，
∴3，
解得m＝0或4，
∴点M的坐标为（0，0）或（0，4）．
14．【解答】解：（1）如图，△A1B1C1即为所求作．
（2）点A1的坐标为（2，1），S△ABC＝3×33×1﹣21×23×2＝3.5．
故答案为：（2，1），3.5．
15．【解答】解：（1）∵∠ACB＝90°，∠A＝35°
∴∠ABC＝90°﹣35°＝55°，
∵三角形ABC沿AB方向向右平移得到三角形DEF，
∴∠E＝∠ABC＝55°；
（2）∵三角形ABC沿AB方向向右平移得到三角形DEF，
∴AB＝DE，
∴AD＝BE＝2cm，
∵AD+BD+BE＝AE＝8cm，
∴DB＝4cm．
16．【解答】解：（1），
∵∠ACB＝90°，∠BAC＝30°，
∴∠ABC＝60°，
∵∠NMQ＝90°，即∠AMN＝90°，
∴∠ANM＝30°，
∵∠MNQ＝45°，
∴∠ANQ＝30°+45°＝75°；
（2）①∠ANQ＝∠AQN时，
此时∠AQN＝∠ANQ＝∠MNQ＝45°，
∴∠NAQ＝90°，
②∠QAN＝∠AQN时，
∵∠NMQ＝90°，∠MNQ＝45°，
∴∠MQN＝45°，
∴∠QAN＝∠AQN＝45°，
③∠ANQ＝∠QAN时，
，
∵∠NMQ＝90°，∠MNQ＝45°，
∴∠NQA＝45°，
∴∠QAN＝∠ANQ（180°﹣∠NQA）＝67.5°，
④∠QNA＝∠QAN时，
，
∵∠NMQ＝90°，∠MNQ＝45°，
∴∠MQN＝45°，
∵∠QNA＝∠QAN，
∴∠QAN∠MQN＝22.5°，
综上，∠QAN的度数为22.5°、45°、67.5°或90°．
17．【解答】解：（1）点B的坐标为（﹣2，4）；
∵A（﹣4，1），D（1，﹣1），C（0，3）
∴由平移得点F的坐标为：（5，1），
故答案为：（﹣2，4）；（5，1）；
（2）如图，△DEF和AD即为所作：
（3）线段AB沿AD的方向平移到DE的过程中扫过的图形为平行四边形ADEB，
．
18．【解答】解：（1）∵点A（0，3），B（﹣2，0），C（4，0），
∴OA＝3，OB＝2，OC＝4，
∴BC＝OB+OC＝4+2＝6，
∴
故答案为：9；
（2）①如图，过点D作DE⊥x轴于E，
由题意，点D坐标为（5，5），则点E坐标为（5，0），
∴CE＝5﹣4＝1，DE＝5，OE＝5，
∴S△ACD＝S梯形AOED﹣S△OAC﹣S△DCE
＝11.5，
∵线段AC的长为5，
∴点D到直线AC的距离为：
2×11.5÷5＝4.6；
②由题意得：，
即，
∴OP＝2，
∵点P在x轴上，
∴点P的坐标为（2，0）或（﹣2，0）．