4.3一次函数的图象培优练习(含答案)
文档属性
| 名称 | 4.3一次函数的图象培优练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 411.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-25 00:00:00 | ||
图片预览


文档简介
4.3一次函数的图象培优练习湘教版2024—2025学年八年级下册
一、选择题
1.若点P在一次函数y=kx+4(k>0)的图象上,则点P一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知(x1,y1),(x2,y2),(x3,y3)为直线y=2x﹣4上的三个点,且x1<x2<x3,则以下判断正确的是( )
A.若x1x3>0,则y1y2>0 B.若x1x2>0,则y1y3>0
C.若x2x3<0,则y2y3>0 D.若x2x3<0,则y1y2>0
3.若a<﹣1,则一次函数y=(a+1)x+1﹣a的图象可能是( )
A.B. C.D.
4.正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2……按如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点A2025的坐标是( )
A.(22024,22025) B.(22024﹣1,22024)
C.(22025,22024) D.(22025﹣1,22025)
5.小明在学习画一次函数的图象时,列表如下:
x … ﹣2 ﹣1 0 1 2 …
y … 7 2 ﹣3 ﹣7 ﹣13 …
小红看了之后说小明把其中一个函数值算错了,这个算错的函数值是( )
A.2 B.﹣3 C.﹣7 D.﹣1
二、填空题
6.如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.﹣1.5)两点,那么当y<0时,自变量x的取值范围是 .
7.如图,点C的坐标是(2,2),A为坐标原点,CB⊥x轴于B,CD⊥y轴于D,点E是线段BC的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为 .
8.直线y=kx+b经过(1,﹣1)、(﹣1,3)、(﹣3,m)三点,则m= .
9.设直线l1:y=kx+k﹣1和直线l2:y=(k+1)x+k(k为正整数)及x轴围成的三角形面积为Sk,则S1+S2+S3+ +S2024的值是 .
10.如图,在平面直角坐标系中,直线交x轴于点A、交y轴于点B,动点P在x轴上,动点Q在线段AB上,满足∠BPQ=∠BAO.当△PQB为等腰三角形时,点P的坐标是 .
三、解答题
11.在平面直角坐标系xOy中,点P的坐标为(m+1,﹣m+3).
(1)试判断点P是否在直线y=﹣x+4上,并说明理由;
(2)若点A是直线y=﹣x+4与y轴的交点,且△AOP的面积为6.求点P的坐标.
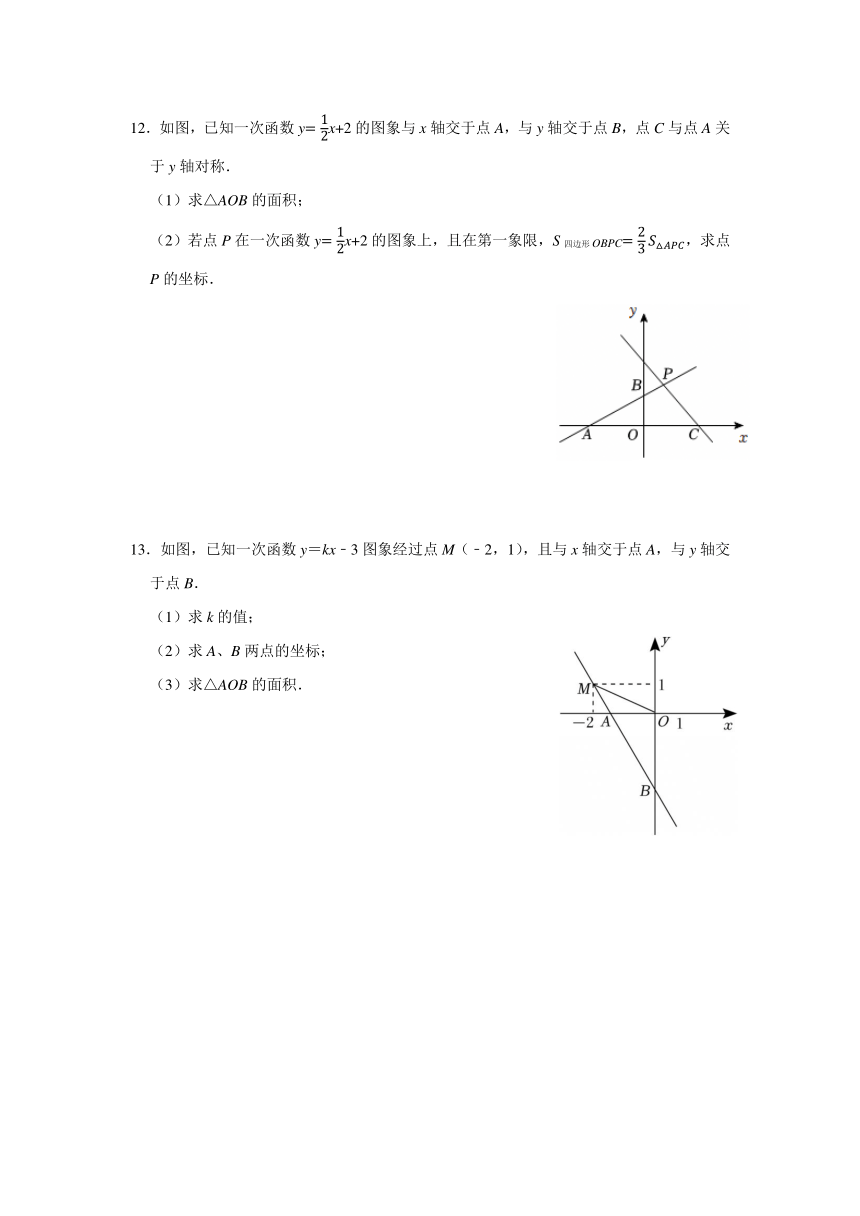
12.如图,已知一次函数yx+2的图象与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求△AOB的面积;
(2)若点P在一次函数yx+2的图象上,且在第一象限,S四边形OBPC,求点P的坐标.
13.如图,已知一次函数y=kx﹣3图象经过点M(﹣2,1),且与x轴交于点A,与y轴交于点B.
(1)求k的值;
(2)求A、B两点的坐标;
(3)求△AOB的面积.
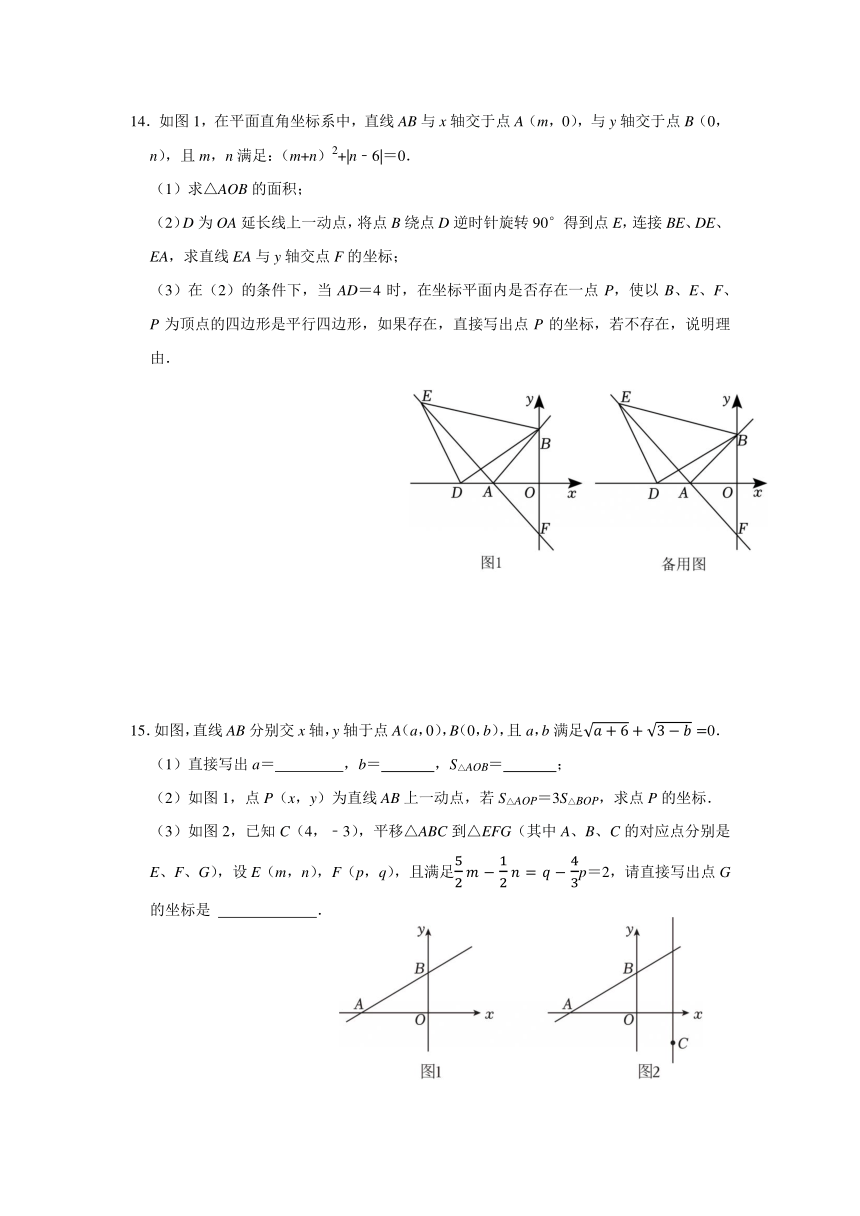
14.如图1,在平面直角坐标系中,直线AB与x轴交于点A(m,0),与y轴交于点B(0,n),且m,n满足:(m+n)2+|n﹣6|=0.
(1)求△AOB的面积;
(2)D为OA延长线上一动点,将点B绕点D逆时针旋转90°得到点E,连接BE、DE、EA,求直线EA与y轴交点F的坐标;
(3)在(2)的条件下,当AD=4时,在坐标平面内是否存在一点P,使以B、E、F、P为顶点的四边形是平行四边形,如果存在,直接写出点P的坐标,若不存在,说明理由.
15.如图,直线AB分别交x轴,y轴于点A(a,0),B(0,b),且a,b满足0.
(1)直接写出a= ,b= ,S△AOB= ;
(2)如图1,点P(x,y)为直线AB上一动点,若S△AOP=3S△BOP,求点P的坐标.
(3)如图2,已知C(4,﹣3),平移△ABC到△EFG(其中A、B、C的对应点分别是E、F、G),设E(m,n),F(p,q),且满足p=2,请直接写出点G的坐标是 .
参考答案
一、选择题
题号 1 2 3 4 5
答案 D D D B C
二、填空题
6.答案为:x<2.
7.答案为:1或3.
8.答案为:7.
9.答案为:.
10.答案为:(4,0)或(1,0)或.
三、解答题
11.【解答】解:(1)点P在直线y=﹣x+4上,理由如下:
∵当x=m+1时,y=﹣(m+1)+4=﹣m+3,
∴点P在直线y=﹣x+4上.
(2)∵点A是直线y=﹣x+4与y轴的交点,
∴A(0,4),
∵点P的坐标为(m+1,﹣m+3),
∴S△AOP|m+1|=6,即m+1=±3,
解得m=﹣4或2,
∴点P的坐标为(﹣3,7)或(3,1).
12.【解答】解:(1)在一次函数yx+2中,当x=0时,y=2;当y=0时,x=﹣4,
∴A(﹣4,0),B(0,2),
∴S△AOB4;
(2)∵点C与点A关于y轴对称.
∴C(4,0),
如图,连接OP,
设点P(m,)(m>0),
S四边形OBPC=S△BOP+S△POC()=2m+4,
S△APC()=2m+8,
∵S四边形OBPC,
∴2m+4(2m+8),解得m=2.
∴P(2,3).
13.【解答】解:(1)∵一次函数y=kx﹣3图象经过点M(﹣2,1),
∴1=﹣2k﹣3,
∴k=﹣2,
∴k的值为﹣2.
(2)当y=0时,﹣2x﹣3=0,
解得:x,
∴点A的坐标为(,0);
∴OA,
当x=0时,y=﹣2×0﹣3=﹣3,
∴点B的坐标为(0,﹣3).
(3)∵点B的坐标为(0,﹣3),
∴OB=3,
∴S△AOBOB OA
3
.
∴△AOB的面积为.
14.【解答】解:(1)∵(m+n)2+|n﹣6|=0,(m+n)2≥0,|n﹣6|≥0,
∴,解得:,
∴A(﹣6,0),B(0,6),
∴OA=﹣6,OB=6,
∴,
∴S△AOB的值为18;
(2)如图所示,过点E作EG⊥x轴于G,
∴∠EGD=90°,
∴∠GED+∠EDG=180°﹣∠EGD=180°﹣90°=90°,
∵△EDB为等腰直角三角形,
∴DE=DB,∠EDB=90°,
∴∠EDG+∠ODB=180°﹣90°=90°,
∴∠GED=∠ODB,
在△EDG和△DBO中,
,
∴△EDG≌△DBO(AAS),
∴DG=BO=6,EG=OD,
设AD=a,
∴OD=OA+AD=6+a=EG,
∴OG=OD+DG=6+a+6=12+a,
∴E点的坐标为(﹣12﹣a,6+a),
设直线EA的解析式为y=kx+b,过点A(﹣6,0),E(﹣12﹣a,6+a),
,
解得:,
∴直线EA的解析式为y=﹣x﹣6,
∴当x=0时,y=﹣6,
∴直线EA与y轴的交点F坐标为(0,﹣6);
(3)存在,点P的坐标为:(16,﹣10),(﹣16,22),(﹣16,﹣2).
∵AD=4,E点的坐标为(﹣12﹣a,6+a),
∴E(﹣16,10),
又F(0,﹣6),B(0,6),B、E、F、P为顶点的四边形是平行四边形,
设P(a,b),当BF为平行四边形的对角线时,,
解得:,则P(16,﹣10),
当BE为对角线时,,
解得:,则P(﹣16,22),
当EF为对角线时,,
解得:,则P(﹣16,﹣2),
点P的坐标为(16,﹣10),(﹣16,22),(﹣16,﹣2).
15.【解答】解:(1)∵a,b满足0,
∴a=﹣6,b=3,
∴OA=6,OB=3,
∴S△AOB9.
故答案为:﹣6;3;9.
(2)设直线AB的解析式为y=kx+b,
∵A(﹣6,0),B(0,3)在函数图象上,
∴,
解得,
∴直线AB的解析式为y,
根据S△AOP=3S△BOP,分三种情况讨论:
①当点P在第一象限时,
∵S△AOP=3S△BOP,
∴,
解得x=3,
∴点P(3,);
②当点P在第二象限时,
∵S△AOP=3S△BOP,
∴,
解得x,
∴P(,),
③当点P在第三象限时,
∵S△AOP<S△BOP,
∴点P在第三象限不存在.
综上分析,满足条件的点P坐标为(3,)或(,);
(3)∵A(﹣6,0),B(0,3),C(4,﹣3),E(m,n),F(p,q),
∴m﹣(﹣6)=p﹣0,n﹣0=q﹣3,
即m+6=p,n=q﹣3,
∵p=2,
∴,
解得,
∴E(3,11),
由A(﹣6,0)平移到E(3,11),可知三角形向右平移9个单位,向上平移11个单位,
∴G(13,8).
故答案为:(13,8).
一、选择题
1.若点P在一次函数y=kx+4(k>0)的图象上,则点P一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知(x1,y1),(x2,y2),(x3,y3)为直线y=2x﹣4上的三个点,且x1<x2<x3,则以下判断正确的是( )
A.若x1x3>0,则y1y2>0 B.若x1x2>0,则y1y3>0
C.若x2x3<0,则y2y3>0 D.若x2x3<0,则y1y2>0
3.若a<﹣1,则一次函数y=(a+1)x+1﹣a的图象可能是( )
A.B. C.D.
4.正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2……按如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点A2025的坐标是( )
A.(22024,22025) B.(22024﹣1,22024)
C.(22025,22024) D.(22025﹣1,22025)
5.小明在学习画一次函数的图象时,列表如下:
x … ﹣2 ﹣1 0 1 2 …
y … 7 2 ﹣3 ﹣7 ﹣13 …
小红看了之后说小明把其中一个函数值算错了,这个算错的函数值是( )
A.2 B.﹣3 C.﹣7 D.﹣1
二、填空题
6.如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.﹣1.5)两点,那么当y<0时,自变量x的取值范围是 .
7.如图,点C的坐标是(2,2),A为坐标原点,CB⊥x轴于B,CD⊥y轴于D,点E是线段BC的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为 .
8.直线y=kx+b经过(1,﹣1)、(﹣1,3)、(﹣3,m)三点,则m= .
9.设直线l1:y=kx+k﹣1和直线l2:y=(k+1)x+k(k为正整数)及x轴围成的三角形面积为Sk,则S1+S2+S3+ +S2024的值是 .
10.如图,在平面直角坐标系中,直线交x轴于点A、交y轴于点B,动点P在x轴上,动点Q在线段AB上,满足∠BPQ=∠BAO.当△PQB为等腰三角形时,点P的坐标是 .
三、解答题
11.在平面直角坐标系xOy中,点P的坐标为(m+1,﹣m+3).
(1)试判断点P是否在直线y=﹣x+4上,并说明理由;
(2)若点A是直线y=﹣x+4与y轴的交点,且△AOP的面积为6.求点P的坐标.
12.如图,已知一次函数yx+2的图象与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求△AOB的面积;
(2)若点P在一次函数yx+2的图象上,且在第一象限,S四边形OBPC,求点P的坐标.
13.如图,已知一次函数y=kx﹣3图象经过点M(﹣2,1),且与x轴交于点A,与y轴交于点B.
(1)求k的值;
(2)求A、B两点的坐标;
(3)求△AOB的面积.
14.如图1,在平面直角坐标系中,直线AB与x轴交于点A(m,0),与y轴交于点B(0,n),且m,n满足:(m+n)2+|n﹣6|=0.
(1)求△AOB的面积;
(2)D为OA延长线上一动点,将点B绕点D逆时针旋转90°得到点E,连接BE、DE、EA,求直线EA与y轴交点F的坐标;
(3)在(2)的条件下,当AD=4时,在坐标平面内是否存在一点P,使以B、E、F、P为顶点的四边形是平行四边形,如果存在,直接写出点P的坐标,若不存在,说明理由.
15.如图,直线AB分别交x轴,y轴于点A(a,0),B(0,b),且a,b满足0.
(1)直接写出a= ,b= ,S△AOB= ;
(2)如图1,点P(x,y)为直线AB上一动点,若S△AOP=3S△BOP,求点P的坐标.
(3)如图2,已知C(4,﹣3),平移△ABC到△EFG(其中A、B、C的对应点分别是E、F、G),设E(m,n),F(p,q),且满足p=2,请直接写出点G的坐标是 .
参考答案
一、选择题
题号 1 2 3 4 5
答案 D D D B C
二、填空题
6.答案为:x<2.
7.答案为:1或3.
8.答案为:7.
9.答案为:.
10.答案为:(4,0)或(1,0)或.
三、解答题
11.【解答】解:(1)点P在直线y=﹣x+4上,理由如下:
∵当x=m+1时,y=﹣(m+1)+4=﹣m+3,
∴点P在直线y=﹣x+4上.
(2)∵点A是直线y=﹣x+4与y轴的交点,
∴A(0,4),
∵点P的坐标为(m+1,﹣m+3),
∴S△AOP|m+1|=6,即m+1=±3,
解得m=﹣4或2,
∴点P的坐标为(﹣3,7)或(3,1).
12.【解答】解:(1)在一次函数yx+2中,当x=0时,y=2;当y=0时,x=﹣4,
∴A(﹣4,0),B(0,2),
∴S△AOB4;
(2)∵点C与点A关于y轴对称.
∴C(4,0),
如图,连接OP,
设点P(m,)(m>0),
S四边形OBPC=S△BOP+S△POC()=2m+4,
S△APC()=2m+8,
∵S四边形OBPC,
∴2m+4(2m+8),解得m=2.
∴P(2,3).
13.【解答】解:(1)∵一次函数y=kx﹣3图象经过点M(﹣2,1),
∴1=﹣2k﹣3,
∴k=﹣2,
∴k的值为﹣2.
(2)当y=0时,﹣2x﹣3=0,
解得:x,
∴点A的坐标为(,0);
∴OA,
当x=0时,y=﹣2×0﹣3=﹣3,
∴点B的坐标为(0,﹣3).
(3)∵点B的坐标为(0,﹣3),
∴OB=3,
∴S△AOBOB OA
3
.
∴△AOB的面积为.
14.【解答】解:(1)∵(m+n)2+|n﹣6|=0,(m+n)2≥0,|n﹣6|≥0,
∴,解得:,
∴A(﹣6,0),B(0,6),
∴OA=﹣6,OB=6,
∴,
∴S△AOB的值为18;
(2)如图所示,过点E作EG⊥x轴于G,
∴∠EGD=90°,
∴∠GED+∠EDG=180°﹣∠EGD=180°﹣90°=90°,
∵△EDB为等腰直角三角形,
∴DE=DB,∠EDB=90°,
∴∠EDG+∠ODB=180°﹣90°=90°,
∴∠GED=∠ODB,
在△EDG和△DBO中,
,
∴△EDG≌△DBO(AAS),
∴DG=BO=6,EG=OD,
设AD=a,
∴OD=OA+AD=6+a=EG,
∴OG=OD+DG=6+a+6=12+a,
∴E点的坐标为(﹣12﹣a,6+a),
设直线EA的解析式为y=kx+b,过点A(﹣6,0),E(﹣12﹣a,6+a),
,
解得:,
∴直线EA的解析式为y=﹣x﹣6,
∴当x=0时,y=﹣6,
∴直线EA与y轴的交点F坐标为(0,﹣6);
(3)存在,点P的坐标为:(16,﹣10),(﹣16,22),(﹣16,﹣2).
∵AD=4,E点的坐标为(﹣12﹣a,6+a),
∴E(﹣16,10),
又F(0,﹣6),B(0,6),B、E、F、P为顶点的四边形是平行四边形,
设P(a,b),当BF为平行四边形的对角线时,,
解得:,则P(16,﹣10),
当BE为对角线时,,
解得:,则P(﹣16,22),
当EF为对角线时,,
解得:,则P(﹣16,﹣2),
点P的坐标为(16,﹣10),(﹣16,22),(﹣16,﹣2).
15.【解答】解:(1)∵a,b满足0,
∴a=﹣6,b=3,
∴OA=6,OB=3,
∴S△AOB9.
故答案为:﹣6;3;9.
(2)设直线AB的解析式为y=kx+b,
∵A(﹣6,0),B(0,3)在函数图象上,
∴,
解得,
∴直线AB的解析式为y,
根据S△AOP=3S△BOP,分三种情况讨论:
①当点P在第一象限时,
∵S△AOP=3S△BOP,
∴,
解得x=3,
∴点P(3,);
②当点P在第二象限时,
∵S△AOP=3S△BOP,
∴,
解得x,
∴P(,),
③当点P在第三象限时,
∵S△AOP<S△BOP,
∴点P在第三象限不存在.
综上分析,满足条件的点P坐标为(3,)或(,);
(3)∵A(﹣6,0),B(0,3),C(4,﹣3),E(m,n),F(p,q),
∴m﹣(﹣6)=p﹣0,n﹣0=q﹣3,
即m+6=p,n=q﹣3,
∵p=2,
∴,
解得,
∴E(3,11),
由A(﹣6,0)平移到E(3,11),可知三角形向右平移9个单位,向上平移11个单位,
∴G(13,8).
故答案为:(13,8).
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
