4.5一次函数的应用培优练习(含答案)
文档属性
| 名称 | 4.5一次函数的应用培优练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 425.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-25 00:00:00 | ||
图片预览




文档简介
4.5一次函数的应用培优练习湘教版2024—2025学年八年级下册
一、选择题
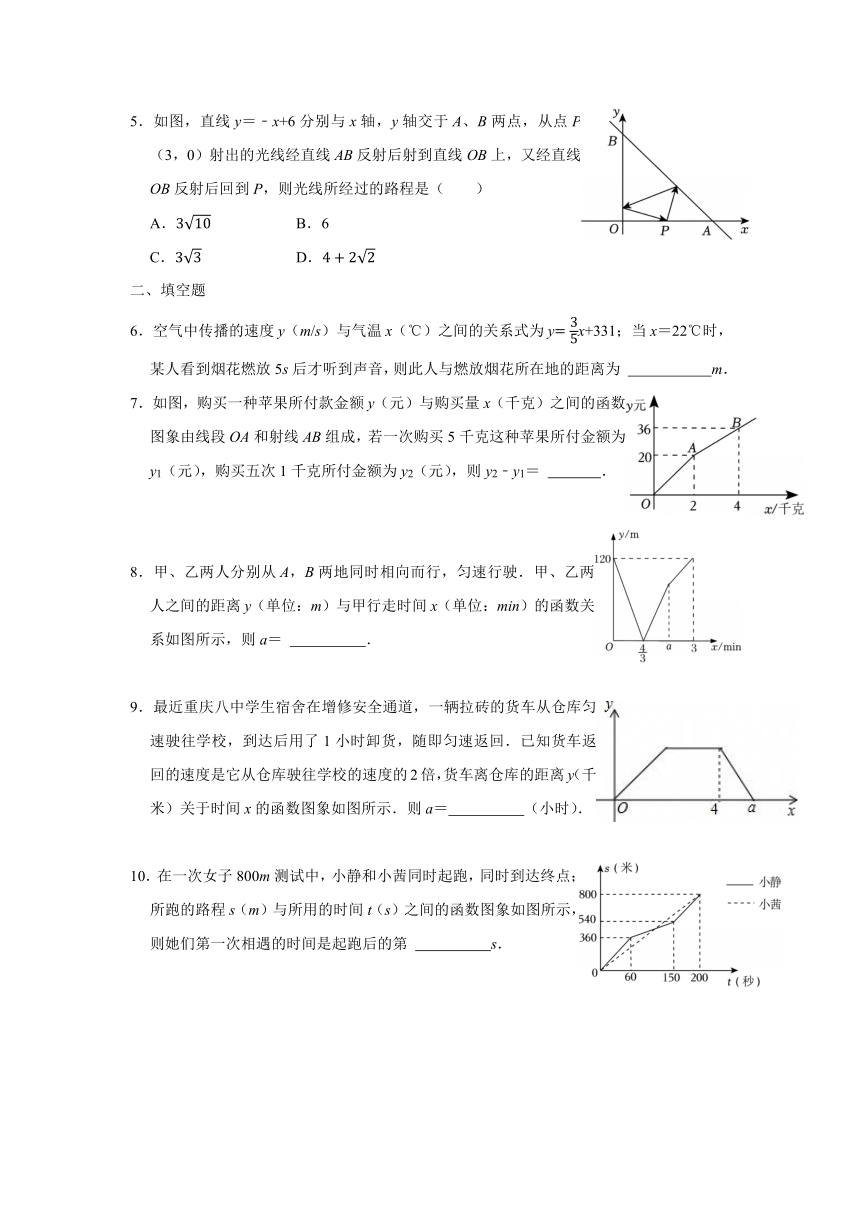
1.一辆货车和一辆轿车先后从甲地出发,沿相同路线匀速驶向乙地.已知甲、乙两地相距150km,如图,OE、CD分别表示货车、轿车离甲地的距离s(km)与货车出发时间t(h)之间的对应关系.根据图象信息,下列说法不正确的是( )
A.轿车的速度为100km/h
B.轿车出发1h后,两车相距10km
C.轿车比货车早到乙地0.5h
D.轿车出发1.25h后追上货车
2.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲、乙两车行驶的时间t(h)之间的函数关系如图所示.有下列结论:①A,B两城相距300km;②乙车比甲车晚出发1h,却早到1h;③乙车出发后2.5h追上甲车;④当甲、乙两车相距50km时,或或.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
3.某生物兴趣小组观察一种植物的生长情况,得到这种植物的高度y(厘米)与观察时间x(天)的函数关系图象如图所示.照此计算,该植物的高度超过12厘米至少需要经过( )
A.16天 B.32天
C.40天 D.56天
4.某湖边公园有一条笔直的健步道,甲、乙两人从起点同方向匀速步行,先到终点的人休息.已知甲先出发3分钟.在整个过程中,甲、乙两人之间距离y(米)与甲出发的时间t(分钟)之间的关系如图所示,则下列结论:①甲步行的速度为75米/分钟;②起点到终点的距离为2700米;③乙行的速度为90米/分钟;④甲走完全程用了39分钟;⑤乙用15分钟追上甲.其中正确的结论是( )
A.①③⑤ B.①②③ C.①③④ D.②④⑤
5.如图,直线y=﹣x+6分别与x轴,y轴交于A、B两点,从点P(3,0)射出的光线经直线AB反射后射到直线OB上,又经直线OB反射后回到P,则光线所经过的路程是( )
A. B.6
C. D.
二、填空题
6.空气中传播的速度y(m/s)与气温x(℃)之间的关系式为yx+331;当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为 m.
7.如图,购买一种苹果所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,若一次购买5千克这种苹果所付金额为y1(元),购买五次1千克所付金额为y2(元),则y2﹣y1= .
8.甲、乙两人分别从A,B两地同时相向而行,匀速行驶.甲、乙两人之间的距离y(单位:m)与甲行走时间x(单位:min)的函数关系如图所示,则a= .
9.最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学校的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a= (小时).
10.在一次女子800m测试中,小静和小茜同时起跑,同时到达终点;所跑的路程s(m)与所用的时间t(s)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第 s.
三、解答题
11.中国新能源汽车正处在快速发展阶段,产销量和出口量均居世界第一,某汽车销售公司针对市场情况,计划购进一批新能源汽车进行销售,据了解购进1辆A型和3辆B型汽车需要75万元,3辆A型和2辆B型汽车需要85万元.
(1)求A、B两种型号的汽车每辆的进价各是多少万元?
(2)该公司准备用正好205万元购进这两种型号的汽车,请你帮助该公司设计部门,写出有哪几种购买方案.
(3)若销售A、B两种型号的汽车每辆分别可获得利润1万元和1.2万元,在(2)方案中如果全部售出,哪种方案获利最大?最大利润是多少万元?
12.一辆货车和一辆轿车先后从A地出发沿同一直道去B地.已知A、B两地相距180km,轿车的速度为120km/h,图中OC、DE分别表示货车、轿车离A地的距离s(km)与时间t(h)之间的函数关系.
(1)求两车相遇时离A地的距离;
(2)求在两车行驶过程中,当t为何值时,两车相距40km.
13.某玩具批发市场A、B玩具的批发价分别为每件30元和50元,张阿姨花1200元购进A、B两种玩具若干件,并分别以每件35元与60元价格出售.设购入A玩具为x件,B玩具为y件.
(1)若张阿姨将玩具全部出售赚了220元,那么张阿姨购进A、B型玩具各多少件?
(2)若要求购进A玩具的数量不得少于B玩具的数量,则怎样分配购进玩具A、B的数量并全部售出才能获得最大利润,此时最大利润为多少?
14.李华同学寒假计划将社会实践活动与勤工俭学相结合,用7500元批发男、女两种款式的羽绒服进行销售,男款每件进价80元,、售价120元;女款进价60元,售价90元,若购进男、女两种款式的羽绒服共100件,其中男款羽绒服不少于65件.
(1)求李华同学男款羽绒服最多批发多少件?
(2)实际销售时,对男款羽绒服以每件优惠a元(0<a<20,a为整数)的价格进行优惠促销活动,女款羽绒服价格不变,则李华同学应如何进货,a为多少元才能获得最大利润?
15.某水果店购进甲、乙两种苹果的进价分别为8元/kg,12元/kg,这两种苹果的销售额y(元)与销售量x(kg)之间的关系如图所示.
(1)求甲种苹果的销售额y与销售量x之间的函数关系式;
(2)求点B的坐标,并写出点B表示的实际意义;
(3)若不计损耗等因素,当甲、乙两种苹果的销售量均为a(a>30)kg时,它们的利润和为1650元,求a的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 D B D A A
二、填空题
6.【解答】解:当x=22时,y22+331=344.2,
则当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为:344.2×5=1721(m),
故答案为:1721.
7.【解答】解:由图象可得,
2千克以内,每千克苹果的单价为:20÷2=10(元),
当x≥2时,设y与x的函数关系式为y=kx+b,
∵点(2,20),(4,36)在该函数图象上,
∴,
解得,
即当x≥2时,y与x的函数关系式为y=8x+4,
y1=8×5+4=44,
y2=10×5=50,
∴y2﹣y1=50﹣44=6,
故答案为:6.
8.【解答】解:由图象可得,甲的速度为:120÷3=40(m/min),
∴乙的速度为12040=90﹣40=50(m/min),
∴a=120÷50=2.4,
故答案为:2.4.
9.【解答】解:由题意可知:
从甲地匀速驶往乙地,到达所用时间为4﹣1=3小时,
返回的速度是它从甲地驶往乙地的速度的2倍,
返回用的时间为3÷2=1.5小时,
所以a=4+1.5=5.5小时.
故答案为:5.5.
10.【解答】解:小茜的速度是4(米/秒),
∴小茜所跑的路程s与所用的时间t之间的函数为s=4t(0≤t≤200).
当60≤t≤150时,设小静所跑的路程s与所用的时间t之间的函数为s=kt+b(k、b为常数,且k≠0),
将坐标(60,360)和(150,540)分别代入s=kt+b,
得,
解得,
∴当60≤t≤150时,小静所跑的路程s与所用的时间t之间的函数为s=2t+240.
当她们第一次相遇时,得,
解得,
∴她们第一次相遇的时间是起跑后的第120秒.
故答案为:120.
三、解答题
11.【解答】解:(1)购进1辆A型和3辆B型汽车需要75万元,3辆A型和2辆B型汽车需要85万元.设A型汽车进价为x万元,B型汽车进价为y万元,代入得:
,
解得,;
∴A型汽车进价为15万元,B型汽车进价为20万元;
(2)该公司准备用正好205万元购进这两种型号的汽车,设A型汽车购买了a辆,B型汽车购买了b辆,依题意得:
15a+20b=205,整理得:,
∵a,b为正整数,
∴(41﹣4b)是3的倍数,
当41﹣4b=3时,,不符合题意,
当41﹣4b=6时,,不符合题意,
当41﹣4b=9时,b=8,符合题意,则a=3,b=8,
当41﹣4b=12时,,不符合题意,
当41﹣4b=15时,,不符合题意,
当41﹣4b=18时,,不符合题意,
当41﹣4b=21时,b=5,符合题意,则a=7,b=5,
当41﹣4b=24时,,不符合题意,
当41﹣4b=27时,,不符合题意,
当41﹣4b=30时,,不符合题意,
当41﹣4b=33时,b=2,符合题意,则a=11,b=2,
当41﹣4b=36时,,不符合题意,
当41﹣4b=39时,,不符合题意,
当41﹣4b=42时,,不符合题意,
综上所述,符合题意的有3中购买方案,分别是第一种方案:A型汽车购买3辆,B型汽车购买8辆;第二种方案:A型汽车购买7辆,B型汽车购买5辆;第三种方案:A型汽车购买11辆,B型汽车购买2辆;
(3)由(2)可得,共有3种购买方案,
第一种方案:A型汽车购买3辆,B型汽车购买8辆,
第二种方案:A型汽车购买7辆,B型汽车购买5辆,
第三种方案:A型汽车购买11辆,B型汽车购买2辆,
∵销售A、B两种型号的汽车每辆分别可获得利润1万元和1.2万元,
∴第一种方案的利润为:3×1+8×1.2=12.6(万元),
第二种方案的利润为:7×1+5×1.2=13(万元),
第三种方案的利润为:11×1+2×1.2=13.4(万元),
∵12.6<13<13.4,
∴第三种方案的利润最大,最大利润为13.4万元.
12.【解答】解:(1)货车的速度为180÷3=60(km/h),
线段OC对应的函数关系式为s=60t(0≤x≤3);
线段DE对应的函数关系式为s=120(t﹣1)=120t﹣120,
当s=180时,得120t﹣120=180,
解得t,
∴线段DE对应的函数关系式为s=120t﹣120(1≤t).
当两车相遇时,得,
解得,
答:两车相遇时离A地的距离为120km.
(2)当0≤t≤1时,当两车相距40km时,得60t=40,
解得t;
当1<t时,当两车相距40km时,得|120t﹣120﹣60t|=40,
解得t或(舍去);
当t≤3时,当两车相距40km时,得180﹣60t=40,
解得t(舍去).
综上,t或.
答:在两车行驶过程中,当t为h或h时,两车相距40km.
13.【解答】解:(1)由题意可得,,
解得,.
答:张阿姨购进A型玩具20件,B型玩具12件;
(2)设利润为w元,
w=(35﹣30)x+(60﹣50)y=5x+10x+240,
∵购进A玩具的数量不得少于B玩具的数量,
∴x,
解得:x≥15,
∵﹣1<0,
∴w随x的增大而减小,
∴当x=15时,w取最大值,最大值为225,
此时y=(1200﹣30×15)÷50=15,
故购进玩具A、B的数量均为15件并全部售出才能获得最大利润,此时最大利润为225元.
14.【解答】解:(1)设李华同学男款羽绒服批发x件,则女款羽绒服批发(100﹣x)件,
由题意可得:80x+60(100﹣x)≤7500,
解得x≤75,
∵男款羽绒服不少于65件,
∴65≤x≤75,
答:李华同学男款羽绒服最多批发75件;
(2)设利润为w元,
w=(120﹣80﹣a)x+(90﹣60)×(100﹣x)=(10﹣a)x+3000,
∵0<a<20,a为整数,65≤x≤75,
∴当0<a<10,a为整数时,w随x的增大而增大,此时a=1,x=75,w取得最大值为3675,100﹣x=25,
当a=10时,w=3000;
当10<a<20,a为整数时,w随x的增大而减小,此时a=11,x=65,w取得最大值为2935,100﹣x=35,
答:李华同学批发男款羽绒服批发75件,女款羽绒服批发25件时,a为1元才能获得最大利润.
15.【解答】解:(1)设甲种苹果销售额y与销售量x之间的函数关系式是y=kx,
∵点(120,2400)在该函数图象上,
∴2400=120k,
解得k=20,
即甲种苹果销售额y甲与销售量x之间的函数关系式是y=20x;
(2)当30≤x≤120时,设乙对应的函数解析式为y=mx+n,
∵点(30,750),(120,2100)在该函数图象上,
∴,
解得,
即当30≤x≤120时,乙对应的函数解析式为y=15x+300,
由可得,
即点B的坐标为(60,1200),点B表示的实际意义是当销售量为60kg时,甲和乙的销售额相同,都是1200元;
(3)由图象可得,
甲种苹果的销售单价为:2400÷120=20(元),
当x≤30时,乙苹果的销售单价为:750÷30=25(元),当x>30时,乙种苹果的销售单价为:(2100﹣750)÷(120﹣30)=15(元),
由题意可得:(20﹣8)a+(25﹣12)×30+(15﹣12)(a﹣30)=1650,
解得a=90,
即a的值为90.
一、选择题
1.一辆货车和一辆轿车先后从甲地出发,沿相同路线匀速驶向乙地.已知甲、乙两地相距150km,如图,OE、CD分别表示货车、轿车离甲地的距离s(km)与货车出发时间t(h)之间的对应关系.根据图象信息,下列说法不正确的是( )
A.轿车的速度为100km/h
B.轿车出发1h后,两车相距10km
C.轿车比货车早到乙地0.5h
D.轿车出发1.25h后追上货车
2.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲、乙两车行驶的时间t(h)之间的函数关系如图所示.有下列结论:①A,B两城相距300km;②乙车比甲车晚出发1h,却早到1h;③乙车出发后2.5h追上甲车;④当甲、乙两车相距50km时,或或.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
3.某生物兴趣小组观察一种植物的生长情况,得到这种植物的高度y(厘米)与观察时间x(天)的函数关系图象如图所示.照此计算,该植物的高度超过12厘米至少需要经过( )
A.16天 B.32天
C.40天 D.56天
4.某湖边公园有一条笔直的健步道,甲、乙两人从起点同方向匀速步行,先到终点的人休息.已知甲先出发3分钟.在整个过程中,甲、乙两人之间距离y(米)与甲出发的时间t(分钟)之间的关系如图所示,则下列结论:①甲步行的速度为75米/分钟;②起点到终点的距离为2700米;③乙行的速度为90米/分钟;④甲走完全程用了39分钟;⑤乙用15分钟追上甲.其中正确的结论是( )
A.①③⑤ B.①②③ C.①③④ D.②④⑤
5.如图,直线y=﹣x+6分别与x轴,y轴交于A、B两点,从点P(3,0)射出的光线经直线AB反射后射到直线OB上,又经直线OB反射后回到P,则光线所经过的路程是( )
A. B.6
C. D.
二、填空题
6.空气中传播的速度y(m/s)与气温x(℃)之间的关系式为yx+331;当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为 m.
7.如图,购买一种苹果所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,若一次购买5千克这种苹果所付金额为y1(元),购买五次1千克所付金额为y2(元),则y2﹣y1= .
8.甲、乙两人分别从A,B两地同时相向而行,匀速行驶.甲、乙两人之间的距离y(单位:m)与甲行走时间x(单位:min)的函数关系如图所示,则a= .
9.最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学校的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a= (小时).
10.在一次女子800m测试中,小静和小茜同时起跑,同时到达终点;所跑的路程s(m)与所用的时间t(s)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第 s.
三、解答题
11.中国新能源汽车正处在快速发展阶段,产销量和出口量均居世界第一,某汽车销售公司针对市场情况,计划购进一批新能源汽车进行销售,据了解购进1辆A型和3辆B型汽车需要75万元,3辆A型和2辆B型汽车需要85万元.
(1)求A、B两种型号的汽车每辆的进价各是多少万元?
(2)该公司准备用正好205万元购进这两种型号的汽车,请你帮助该公司设计部门,写出有哪几种购买方案.
(3)若销售A、B两种型号的汽车每辆分别可获得利润1万元和1.2万元,在(2)方案中如果全部售出,哪种方案获利最大?最大利润是多少万元?
12.一辆货车和一辆轿车先后从A地出发沿同一直道去B地.已知A、B两地相距180km,轿车的速度为120km/h,图中OC、DE分别表示货车、轿车离A地的距离s(km)与时间t(h)之间的函数关系.
(1)求两车相遇时离A地的距离;
(2)求在两车行驶过程中,当t为何值时,两车相距40km.
13.某玩具批发市场A、B玩具的批发价分别为每件30元和50元,张阿姨花1200元购进A、B两种玩具若干件,并分别以每件35元与60元价格出售.设购入A玩具为x件,B玩具为y件.
(1)若张阿姨将玩具全部出售赚了220元,那么张阿姨购进A、B型玩具各多少件?
(2)若要求购进A玩具的数量不得少于B玩具的数量,则怎样分配购进玩具A、B的数量并全部售出才能获得最大利润,此时最大利润为多少?
14.李华同学寒假计划将社会实践活动与勤工俭学相结合,用7500元批发男、女两种款式的羽绒服进行销售,男款每件进价80元,、售价120元;女款进价60元,售价90元,若购进男、女两种款式的羽绒服共100件,其中男款羽绒服不少于65件.
(1)求李华同学男款羽绒服最多批发多少件?
(2)实际销售时,对男款羽绒服以每件优惠a元(0<a<20,a为整数)的价格进行优惠促销活动,女款羽绒服价格不变,则李华同学应如何进货,a为多少元才能获得最大利润?
15.某水果店购进甲、乙两种苹果的进价分别为8元/kg,12元/kg,这两种苹果的销售额y(元)与销售量x(kg)之间的关系如图所示.
(1)求甲种苹果的销售额y与销售量x之间的函数关系式;
(2)求点B的坐标,并写出点B表示的实际意义;
(3)若不计损耗等因素,当甲、乙两种苹果的销售量均为a(a>30)kg时,它们的利润和为1650元,求a的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 D B D A A
二、填空题
6.【解答】解:当x=22时,y22+331=344.2,
则当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为:344.2×5=1721(m),
故答案为:1721.
7.【解答】解:由图象可得,
2千克以内,每千克苹果的单价为:20÷2=10(元),
当x≥2时,设y与x的函数关系式为y=kx+b,
∵点(2,20),(4,36)在该函数图象上,
∴,
解得,
即当x≥2时,y与x的函数关系式为y=8x+4,
y1=8×5+4=44,
y2=10×5=50,
∴y2﹣y1=50﹣44=6,
故答案为:6.
8.【解答】解:由图象可得,甲的速度为:120÷3=40(m/min),
∴乙的速度为12040=90﹣40=50(m/min),
∴a=120÷50=2.4,
故答案为:2.4.
9.【解答】解:由题意可知:
从甲地匀速驶往乙地,到达所用时间为4﹣1=3小时,
返回的速度是它从甲地驶往乙地的速度的2倍,
返回用的时间为3÷2=1.5小时,
所以a=4+1.5=5.5小时.
故答案为:5.5.
10.【解答】解:小茜的速度是4(米/秒),
∴小茜所跑的路程s与所用的时间t之间的函数为s=4t(0≤t≤200).
当60≤t≤150时,设小静所跑的路程s与所用的时间t之间的函数为s=kt+b(k、b为常数,且k≠0),
将坐标(60,360)和(150,540)分别代入s=kt+b,
得,
解得,
∴当60≤t≤150时,小静所跑的路程s与所用的时间t之间的函数为s=2t+240.
当她们第一次相遇时,得,
解得,
∴她们第一次相遇的时间是起跑后的第120秒.
故答案为:120.
三、解答题
11.【解答】解:(1)购进1辆A型和3辆B型汽车需要75万元,3辆A型和2辆B型汽车需要85万元.设A型汽车进价为x万元,B型汽车进价为y万元,代入得:
,
解得,;
∴A型汽车进价为15万元,B型汽车进价为20万元;
(2)该公司准备用正好205万元购进这两种型号的汽车,设A型汽车购买了a辆,B型汽车购买了b辆,依题意得:
15a+20b=205,整理得:,
∵a,b为正整数,
∴(41﹣4b)是3的倍数,
当41﹣4b=3时,,不符合题意,
当41﹣4b=6时,,不符合题意,
当41﹣4b=9时,b=8,符合题意,则a=3,b=8,
当41﹣4b=12时,,不符合题意,
当41﹣4b=15时,,不符合题意,
当41﹣4b=18时,,不符合题意,
当41﹣4b=21时,b=5,符合题意,则a=7,b=5,
当41﹣4b=24时,,不符合题意,
当41﹣4b=27时,,不符合题意,
当41﹣4b=30时,,不符合题意,
当41﹣4b=33时,b=2,符合题意,则a=11,b=2,
当41﹣4b=36时,,不符合题意,
当41﹣4b=39时,,不符合题意,
当41﹣4b=42时,,不符合题意,
综上所述,符合题意的有3中购买方案,分别是第一种方案:A型汽车购买3辆,B型汽车购买8辆;第二种方案:A型汽车购买7辆,B型汽车购买5辆;第三种方案:A型汽车购买11辆,B型汽车购买2辆;
(3)由(2)可得,共有3种购买方案,
第一种方案:A型汽车购买3辆,B型汽车购买8辆,
第二种方案:A型汽车购买7辆,B型汽车购买5辆,
第三种方案:A型汽车购买11辆,B型汽车购买2辆,
∵销售A、B两种型号的汽车每辆分别可获得利润1万元和1.2万元,
∴第一种方案的利润为:3×1+8×1.2=12.6(万元),
第二种方案的利润为:7×1+5×1.2=13(万元),
第三种方案的利润为:11×1+2×1.2=13.4(万元),
∵12.6<13<13.4,
∴第三种方案的利润最大,最大利润为13.4万元.
12.【解答】解:(1)货车的速度为180÷3=60(km/h),
线段OC对应的函数关系式为s=60t(0≤x≤3);
线段DE对应的函数关系式为s=120(t﹣1)=120t﹣120,
当s=180时,得120t﹣120=180,
解得t,
∴线段DE对应的函数关系式为s=120t﹣120(1≤t).
当两车相遇时,得,
解得,
答:两车相遇时离A地的距离为120km.
(2)当0≤t≤1时,当两车相距40km时,得60t=40,
解得t;
当1<t时,当两车相距40km时,得|120t﹣120﹣60t|=40,
解得t或(舍去);
当t≤3时,当两车相距40km时,得180﹣60t=40,
解得t(舍去).
综上,t或.
答:在两车行驶过程中,当t为h或h时,两车相距40km.
13.【解答】解:(1)由题意可得,,
解得,.
答:张阿姨购进A型玩具20件,B型玩具12件;
(2)设利润为w元,
w=(35﹣30)x+(60﹣50)y=5x+10x+240,
∵购进A玩具的数量不得少于B玩具的数量,
∴x,
解得:x≥15,
∵﹣1<0,
∴w随x的增大而减小,
∴当x=15时,w取最大值,最大值为225,
此时y=(1200﹣30×15)÷50=15,
故购进玩具A、B的数量均为15件并全部售出才能获得最大利润,此时最大利润为225元.
14.【解答】解:(1)设李华同学男款羽绒服批发x件,则女款羽绒服批发(100﹣x)件,
由题意可得:80x+60(100﹣x)≤7500,
解得x≤75,
∵男款羽绒服不少于65件,
∴65≤x≤75,
答:李华同学男款羽绒服最多批发75件;
(2)设利润为w元,
w=(120﹣80﹣a)x+(90﹣60)×(100﹣x)=(10﹣a)x+3000,
∵0<a<20,a为整数,65≤x≤75,
∴当0<a<10,a为整数时,w随x的增大而增大,此时a=1,x=75,w取得最大值为3675,100﹣x=25,
当a=10时,w=3000;
当10<a<20,a为整数时,w随x的增大而减小,此时a=11,x=65,w取得最大值为2935,100﹣x=35,
答:李华同学批发男款羽绒服批发75件,女款羽绒服批发25件时,a为1元才能获得最大利润.
15.【解答】解:(1)设甲种苹果销售额y与销售量x之间的函数关系式是y=kx,
∵点(120,2400)在该函数图象上,
∴2400=120k,
解得k=20,
即甲种苹果销售额y甲与销售量x之间的函数关系式是y=20x;
(2)当30≤x≤120时,设乙对应的函数解析式为y=mx+n,
∵点(30,750),(120,2100)在该函数图象上,
∴,
解得,
即当30≤x≤120时,乙对应的函数解析式为y=15x+300,
由可得,
即点B的坐标为(60,1200),点B表示的实际意义是当销售量为60kg时,甲和乙的销售额相同,都是1200元;
(3)由图象可得,
甲种苹果的销售单价为:2400÷120=20(元),
当x≤30时,乙苹果的销售单价为:750÷30=25(元),当x>30时,乙种苹果的销售单价为:(2100﹣750)÷(120﹣30)=15(元),
由题意可得:(20﹣8)a+(25﹣12)×30+(15﹣12)(a﹣30)=1650,
解得a=90,
即a的值为90.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
