4.1光的折射 课件(共30张PPT)
文档属性
| 名称 | 4.1光的折射 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 56.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-25 19:43:46 | ||
图片预览








文档简介
(共30张PPT)
第四章第一节光的折射
人教版选择性必修一
目录
1.学习目标
2.光的折射特点
3.折射率的概念
4.典型例题分析
5.实验测量玻璃砖的折射率
6.课堂总结
1. 认识光的反射及折射现象,知道法线、入射角、反射角、折射角的含义。
2. 通过实验探究,理解折射率的概念和光的折射定律。
3. 会测量玻璃等材料的折射率,通过实验体会光线模型的构建过程。
学习目标:
光的折射特点
光的折射
城市冯家的摄影照片利用的光的反射现象
铅笔“折断” 是不是光的反射呢?
如果不是,那么它们属于哪种现象呢?
光的折射
光的折射
介质1
介质2
光从第 1 种介质射到该介质与第 2 种介质的分界面时,一部分光会返回到第1种介质,这个现象叫作光的反射;另一部分光会进入第2种介质,这个现象叫作光的折射。
光在反射时遵从反射定律,光在折射时遵从什么规律呢?
光的折射
光的折射
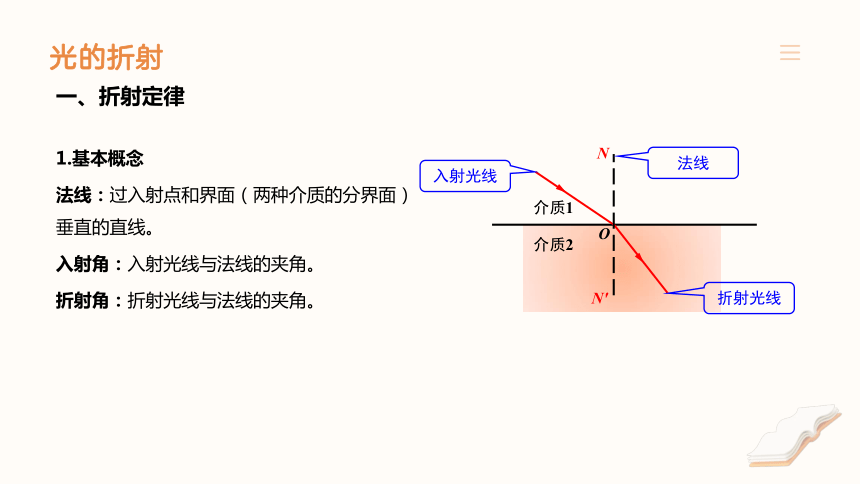
1.基本概念
法线:过入射点和界面(两种介质的分界面)垂直的直线。
入射角:入射光线与法线的夹角。
折射角:折射光线与法线的夹角。
一、折射定律
介质1
介质2
入射光线
折射光线
N
O
N'
法线
光的折射
2.折射定律
折射光线、入射光线、法线在同一平面内。
折射光线和入射光线分居法线两侧。
入射角的正弦与折射角的正弦成正比, 即: n12
式中n12是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
介质1
介质2
入射光线
折射光线
N
O
N'
法线
光的折射
空气
水或玻璃
入射角
折射角
N
O
N'
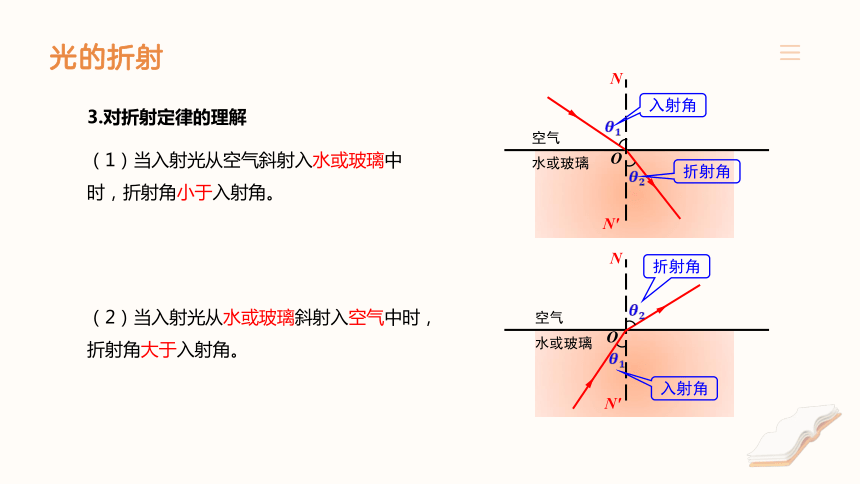
3.对折射定律的理解
(1)当入射光从空气斜射入水或玻璃中时,折射角小于入射角。
空气
水或玻璃
N
N'
(2)当入射光从水或玻璃斜射入空气中时,折射角大于入射角。
入射角
折射角
O
光的折射
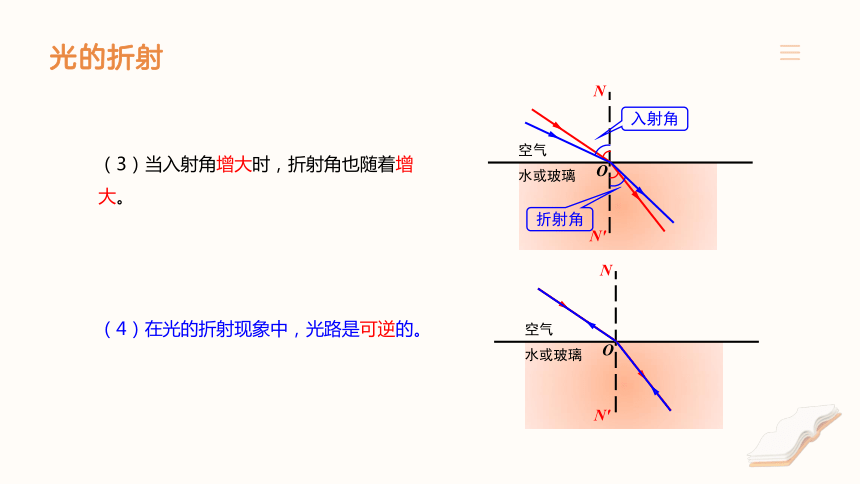
(3)当入射角增大时,折射角也随着增大。
空气
水或玻璃
N
N'
入射角
折射角
O
空气
水或玻璃
N
N'
O
(4)在光的折射现象中,光路是可逆的。
光的折射率
光的折射
1.光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫作这种介质的绝对折射率,简称折射率,用符号 n 表示。
2. 光在不同介质中的传播速度不同;某种介质的折射率等于光在真空中的传播速度 c 与光在这种介质中的传播速度 v 之比,
即:n
注意:真空折射率为1,空气折射率近似为1,且大于1。
二、折射率
光的折射
3.下表列出了几种介质的折射率。
4.由于光在真空中的传播速度 c 大于光在任何其他介质中的传播速度 v,因而任何介质的折射率 n 都大于 1。
典型例题分析
光的折射
例1.如 图所示,光线以入射角θ1从空气射向折射率n= 的玻璃表面。
(1)当入射角θ1=45°时,反射光线与折射光线间的夹角θ为多大?
(2)当入射角θ1为多少时,反射光线与折射光线垂直?
解: (1)由折射定律有n= ,解得sin θ2= = ,则θ2=30°,由反射定律得θ′1=θ1=45°,
由几何关系可知反射光线与折射光线间的夹角为θ=105°。
(2)当反射光线与折射光线垂直时,有θ′1+θ2=90°
则n= = = =tan θ1=
故θ1=arctan 。
光的折射
例2.河中有条小鱼,某时刻小鱼的实际深度为H,一人从水面正上方往水中看,他感觉到的小鱼的深度为多大?(设水的折射率为n)
解:如图所示,设小鱼在S处,从鱼反射出的光线SO垂直水面射出,光线SO1与SO间的夹角很小。因一般人的瞳孔的线度为2~3 mm,θ1、θ2为一组对应的折射角和入射角,可知θ1、θ2均很小。由数学知识知:
sin θ1≈tan θ1= ,sin θ2≈tan θ2=
由折射定律得:n= = = ,得h=
即他感觉到的小鱼的深度为 。
光的折射
例3.如图所示的装置可以测量棱镜的折射率。ABC表示待测直角棱镜的横截面,
棱镜的顶角为α,紧贴直角边AC放置一块平面镜。一光线SO射到棱镜的AB面上,
适当调整SO的方向,当SO与AB成β角时,从AB面射出的光线与SO重合。
(1)画出光线SO进入棱镜的折射光线;
(2)求出棱镜的折射率n。
解析:(1)光路如图所示。
(2)入射角i=90°-β
要使从AB面射出的光线与SO重合,则AB面上折射光线必须与AC面垂直,
由几何知识得到,折射角r=α
则折射率n= = 。
光的折射
例1. 一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
光的折射
设液体的折射率为n,由折射定律有:
n sin i1=sin r1 ①
n sin i2=sin r2 ②
由题意知r1+r2=90° ③
联立①②③式得:n2 = ④
由几何关系可知:sin i1= = ⑤
sin i2= = ⑥
联立④⑤⑥式得:n ≈ 1.55
例4.一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
测量玻璃砖的折射率
光的折射
光的折射
1.实验原理
用插针法确定光路,找出跟入射光线相对应的折射光线,用量角器测出入射角θ1和折射角θ2,根据折射定律计算出玻璃的折射率n= .
2.实验器材
玻璃砖、白纸、木板、大头针四枚、图钉四枚、量角器、三角板(或直尺)、铅笔.
3.实验步骤
(1)如图所示,将白纸用图钉钉在平木板上.
(2)在白纸上画出一条直线aa′作为界面(线),
过aa′上的一点O画出界面的法线NN′,并
画一条线段AO作为入射光线.
三、测玻璃砖的折射率
光的折射
(3)把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′.
(4)在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像.再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置.
(5)移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向.
(6)连接OO′,入射角θ1=∠AON,折射角θ2=∠O′ON′,用量角器量出入射角和折射角.
(7)用上述方法测出入射角分别为30°、45°、60°时的折射角.
光的折射
4.数据处理
(1)图象法:求出多组对应的入射角与折射角的正弦值,作出
sin θ1 --sin θ2图象,由n= 可知图象应为直线,如图
所示,其斜率为折射率.
(2)单位圆法:在不使用量角器的情况下,可以用画单位圆法.
①以入射点O为圆心,以一定长度R为半径画圆,交入射光线OA于E点,
交折射光线OO′于E′点,过E 作NN′的垂线EH,过E′作NN′的垂线E′H′,
如图所示.
②由图中关系sin θ1= ,sin θ2= ,OE=OE ′=R,
则n= 只要用刻度尺测出EH、E′H ′的长度就可以求出n.
光的折射
例1.如图所示,用“插针法”测量一等腰三角形玻璃砖(侧面分别记为A和 B、顶角大小为 )的折射率。
①在白纸上画一条直线ab,并画出其垂线cd,交于O点;
②将侧面A沿ab放置,并确定侧面B的位置ef
③在cd上坚直插上大头针P1和P2,从侧面B透过玻璃砖观察P1和P2,插上大头针P3,要求P3能挡住 (选填“P1”、“P2”或“P1和P2”)的虚像;
④确定出射光线的位置 (选填“需要”或“不需要”第四枚大头针;
⑤撤去玻璃砖和大头针,测得出射光线与直线ef的夹角为α,则玻璃砖折射率 n= 。
【答案】 P1和P2 不需要
【详解】③[1]要求P1和P2在一条光线上,该光线透过玻璃砖后过P3,故P3要能挡住P1和P2的虚像;
④[2]cd与ab垂直,则过P1和P2的光线与ab垂直,光垂直入射时传播方向不变,可确定ef边上的入射点,此时只需要找到折射光线上的一点即可确定出射光线,不需要插第四枚大头针;
⑤[3]根据几何关系可知入射角为,折射角为 ,故
光的折射
例2.用激光测玻璃砖折射率的实验中,玻璃砖与屏P平行放置,从另一侧用激光笔以一定角度照射,此时在屏上的S1处有激光点,移走玻璃砖,光点移到S2处,回答下列问题:
(1)请画出激光束经玻璃折射后完整的光路图 ;
(2)已经测出AB = l1,OA = l2,S1S2= l3,则折射率n = (用l1、l2、l3表示);
(3)若改用宽ab更小的玻璃砖做实验,则S1S2间的距离会 (填“变大”,“变小”或“不变”)。
答案
变小
光的折射
【详解】(1)根据题意画出光路图如下图所示
(2)设光线在C点的入射角为θ、折射角为α,根据折射定律有
nsinθ = sinα
由于射入玻璃砖的入射角是射出玻璃砖的折射角,则
S1S2= CB
根据几何关系可知
联立解得
(3)若改用宽ab更小的玻璃砖做实验,则画出光路图如下
可看出S1S2间的距离变小。
课堂总结
光的折射
1.折射定律
折射光线、入射光线、法线在同一平面内。折射光线和入射光线分居法线两侧。入射角的正弦与折射角的正弦成正比, 即: n12
式中n12是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
2.理解(1)当入射光从空气斜射入水或玻璃中时,折射角小于入射角。
(2)当入射光从水或玻璃斜射入空气中时,折射角大于入射角。
(3)当入射角增大时,折射角也随着增大。
(4)在光的折射现象中,光路是可逆的。
3.测量玻璃的折射率:插针法
本课小结
第四章第一节光的折射
人教版选择性必修一
目录
1.学习目标
2.光的折射特点
3.折射率的概念
4.典型例题分析
5.实验测量玻璃砖的折射率
6.课堂总结
1. 认识光的反射及折射现象,知道法线、入射角、反射角、折射角的含义。
2. 通过实验探究,理解折射率的概念和光的折射定律。
3. 会测量玻璃等材料的折射率,通过实验体会光线模型的构建过程。
学习目标:
光的折射特点
光的折射
城市冯家的摄影照片利用的光的反射现象
铅笔“折断” 是不是光的反射呢?
如果不是,那么它们属于哪种现象呢?
光的折射
光的折射
介质1
介质2
光从第 1 种介质射到该介质与第 2 种介质的分界面时,一部分光会返回到第1种介质,这个现象叫作光的反射;另一部分光会进入第2种介质,这个现象叫作光的折射。
光在反射时遵从反射定律,光在折射时遵从什么规律呢?
光的折射
光的折射
1.基本概念
法线:过入射点和界面(两种介质的分界面)垂直的直线。
入射角:入射光线与法线的夹角。
折射角:折射光线与法线的夹角。
一、折射定律
介质1
介质2
入射光线
折射光线
N
O
N'
法线
光的折射
2.折射定律
折射光线、入射光线、法线在同一平面内。
折射光线和入射光线分居法线两侧。
入射角的正弦与折射角的正弦成正比, 即: n12
式中n12是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
介质1
介质2
入射光线
折射光线
N
O
N'
法线
光的折射
空气
水或玻璃
入射角
折射角
N
O
N'
3.对折射定律的理解
(1)当入射光从空气斜射入水或玻璃中时,折射角小于入射角。
空气
水或玻璃
N
N'
(2)当入射光从水或玻璃斜射入空气中时,折射角大于入射角。
入射角
折射角
O
光的折射
(3)当入射角增大时,折射角也随着增大。
空气
水或玻璃
N
N'
入射角
折射角
O
空气
水或玻璃
N
N'
O
(4)在光的折射现象中,光路是可逆的。
光的折射率
光的折射
1.光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫作这种介质的绝对折射率,简称折射率,用符号 n 表示。
2. 光在不同介质中的传播速度不同;某种介质的折射率等于光在真空中的传播速度 c 与光在这种介质中的传播速度 v 之比,
即:n
注意:真空折射率为1,空气折射率近似为1,且大于1。
二、折射率
光的折射
3.下表列出了几种介质的折射率。
4.由于光在真空中的传播速度 c 大于光在任何其他介质中的传播速度 v,因而任何介质的折射率 n 都大于 1。
典型例题分析
光的折射
例1.如 图所示,光线以入射角θ1从空气射向折射率n= 的玻璃表面。
(1)当入射角θ1=45°时,反射光线与折射光线间的夹角θ为多大?
(2)当入射角θ1为多少时,反射光线与折射光线垂直?
解: (1)由折射定律有n= ,解得sin θ2= = ,则θ2=30°,由反射定律得θ′1=θ1=45°,
由几何关系可知反射光线与折射光线间的夹角为θ=105°。
(2)当反射光线与折射光线垂直时,有θ′1+θ2=90°
则n= = = =tan θ1=
故θ1=arctan 。
光的折射
例2.河中有条小鱼,某时刻小鱼的实际深度为H,一人从水面正上方往水中看,他感觉到的小鱼的深度为多大?(设水的折射率为n)
解:如图所示,设小鱼在S处,从鱼反射出的光线SO垂直水面射出,光线SO1与SO间的夹角很小。因一般人的瞳孔的线度为2~3 mm,θ1、θ2为一组对应的折射角和入射角,可知θ1、θ2均很小。由数学知识知:
sin θ1≈tan θ1= ,sin θ2≈tan θ2=
由折射定律得:n= = = ,得h=
即他感觉到的小鱼的深度为 。
光的折射
例3.如图所示的装置可以测量棱镜的折射率。ABC表示待测直角棱镜的横截面,
棱镜的顶角为α,紧贴直角边AC放置一块平面镜。一光线SO射到棱镜的AB面上,
适当调整SO的方向,当SO与AB成β角时,从AB面射出的光线与SO重合。
(1)画出光线SO进入棱镜的折射光线;
(2)求出棱镜的折射率n。
解析:(1)光路如图所示。
(2)入射角i=90°-β
要使从AB面射出的光线与SO重合,则AB面上折射光线必须与AC面垂直,
由几何知识得到,折射角r=α
则折射率n= = 。
光的折射
例1. 一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
光的折射
设液体的折射率为n,由折射定律有:
n sin i1=sin r1 ①
n sin i2=sin r2 ②
由题意知r1+r2=90° ③
联立①②③式得:n2 = ④
由几何关系可知:sin i1= = ⑤
sin i2= = ⑥
联立④⑤⑥式得:n ≈ 1.55
例4.一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
测量玻璃砖的折射率
光的折射
光的折射
1.实验原理
用插针法确定光路,找出跟入射光线相对应的折射光线,用量角器测出入射角θ1和折射角θ2,根据折射定律计算出玻璃的折射率n= .
2.实验器材
玻璃砖、白纸、木板、大头针四枚、图钉四枚、量角器、三角板(或直尺)、铅笔.
3.实验步骤
(1)如图所示,将白纸用图钉钉在平木板上.
(2)在白纸上画出一条直线aa′作为界面(线),
过aa′上的一点O画出界面的法线NN′,并
画一条线段AO作为入射光线.
三、测玻璃砖的折射率
光的折射
(3)把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′.
(4)在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像.再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置.
(5)移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向.
(6)连接OO′,入射角θ1=∠AON,折射角θ2=∠O′ON′,用量角器量出入射角和折射角.
(7)用上述方法测出入射角分别为30°、45°、60°时的折射角.
光的折射
4.数据处理
(1)图象法:求出多组对应的入射角与折射角的正弦值,作出
sin θ1 --sin θ2图象,由n= 可知图象应为直线,如图
所示,其斜率为折射率.
(2)单位圆法:在不使用量角器的情况下,可以用画单位圆法.
①以入射点O为圆心,以一定长度R为半径画圆,交入射光线OA于E点,
交折射光线OO′于E′点,过E 作NN′的垂线EH,过E′作NN′的垂线E′H′,
如图所示.
②由图中关系sin θ1= ,sin θ2= ,OE=OE ′=R,
则n= 只要用刻度尺测出EH、E′H ′的长度就可以求出n.
光的折射
例1.如图所示,用“插针法”测量一等腰三角形玻璃砖(侧面分别记为A和 B、顶角大小为 )的折射率。
①在白纸上画一条直线ab,并画出其垂线cd,交于O点;
②将侧面A沿ab放置,并确定侧面B的位置ef
③在cd上坚直插上大头针P1和P2,从侧面B透过玻璃砖观察P1和P2,插上大头针P3,要求P3能挡住 (选填“P1”、“P2”或“P1和P2”)的虚像;
④确定出射光线的位置 (选填“需要”或“不需要”第四枚大头针;
⑤撤去玻璃砖和大头针,测得出射光线与直线ef的夹角为α,则玻璃砖折射率 n= 。
【答案】 P1和P2 不需要
【详解】③[1]要求P1和P2在一条光线上,该光线透过玻璃砖后过P3,故P3要能挡住P1和P2的虚像;
④[2]cd与ab垂直,则过P1和P2的光线与ab垂直,光垂直入射时传播方向不变,可确定ef边上的入射点,此时只需要找到折射光线上的一点即可确定出射光线,不需要插第四枚大头针;
⑤[3]根据几何关系可知入射角为,折射角为 ,故
光的折射
例2.用激光测玻璃砖折射率的实验中,玻璃砖与屏P平行放置,从另一侧用激光笔以一定角度照射,此时在屏上的S1处有激光点,移走玻璃砖,光点移到S2处,回答下列问题:
(1)请画出激光束经玻璃折射后完整的光路图 ;
(2)已经测出AB = l1,OA = l2,S1S2= l3,则折射率n = (用l1、l2、l3表示);
(3)若改用宽ab更小的玻璃砖做实验,则S1S2间的距离会 (填“变大”,“变小”或“不变”)。
答案
变小
光的折射
【详解】(1)根据题意画出光路图如下图所示
(2)设光线在C点的入射角为θ、折射角为α,根据折射定律有
nsinθ = sinα
由于射入玻璃砖的入射角是射出玻璃砖的折射角,则
S1S2= CB
根据几何关系可知
联立解得
(3)若改用宽ab更小的玻璃砖做实验,则画出光路图如下
可看出S1S2间的距离变小。
课堂总结
光的折射
1.折射定律
折射光线、入射光线、法线在同一平面内。折射光线和入射光线分居法线两侧。入射角的正弦与折射角的正弦成正比, 即: n12
式中n12是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
2.理解(1)当入射光从空气斜射入水或玻璃中时,折射角小于入射角。
(2)当入射光从水或玻璃斜射入空气中时,折射角大于入射角。
(3)当入射角增大时,折射角也随着增大。
(4)在光的折射现象中,光路是可逆的。
3.测量玻璃的折射率:插针法
本课小结
