6.2平行四边形的判定培优专题训练(含答案)
文档属性
| 名称 | 6.2平行四边形的判定培优专题训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 974.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 16:57:51 | ||
图片预览



文档简介
6.2平行四边形的判定培优专题训练北师大版2024—2025八年级下册
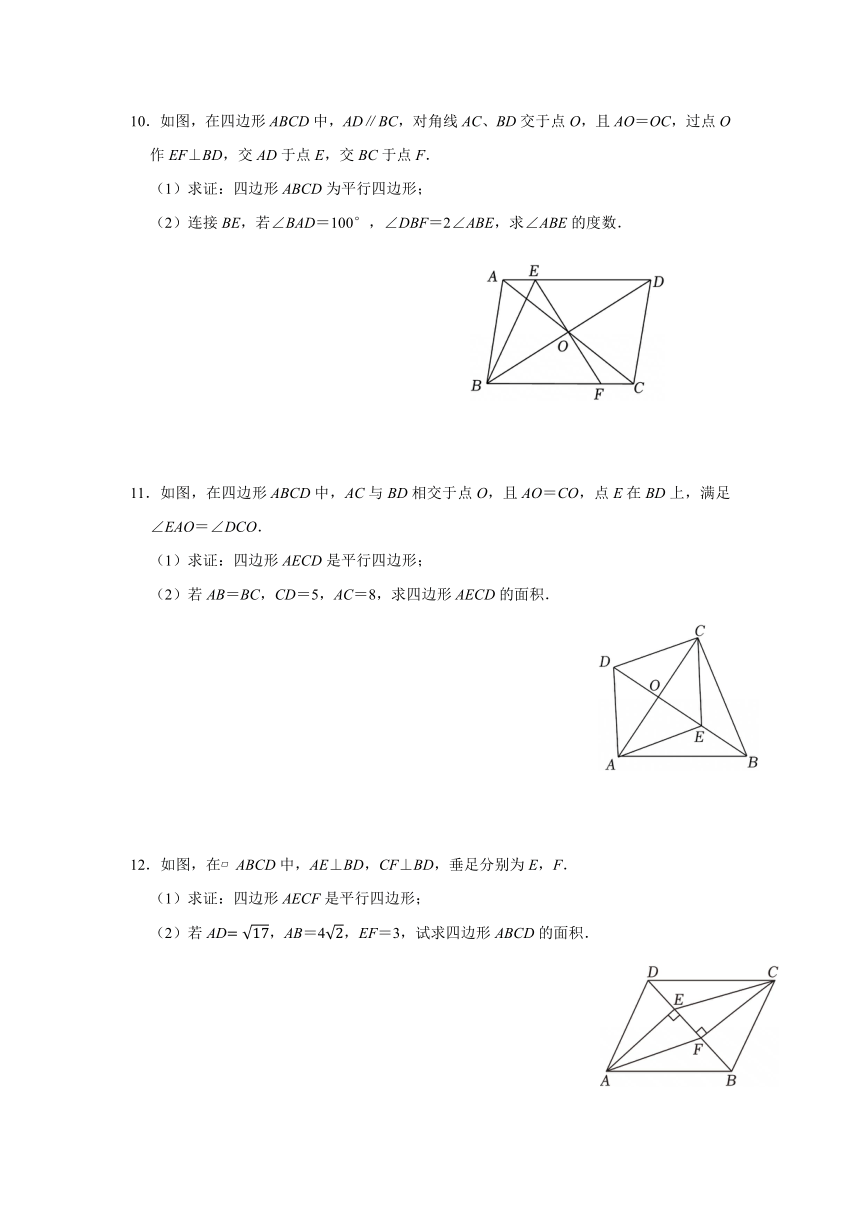
1.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
2.如图,在 ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.求证:
(1)DE=BF;
(2)四边形AFCE是平行四边形.
3.已知:如图,在 ABCD中,E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AECF是平行四边形;
(2)若AD⊥BD,AB=5,AD=3,且EF﹣AF=2,求DE的长.
4.如图,在四边形ABCD中,对角线AC与BD相交于点O,且AO=CO,AD∥BC.
(1)求证:四边形ABCD为平行四边形;
(2)若AB=10,OA=6,BD=16.
①求∠BOA的度数;
②求四边形ABCD的面积.
5.在平行四边形ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.
6.如图,在 ABCD中,E,F两点分别在边AB,CD上,连接DE,BF,AF,且∠ADE=∠CBF.
(1)求证:四边形DEBF为平行四边形;
(2)若AF平分∠BAD,DE⊥AB,且AD=6,AF=10,求AE的长.
7.如图,已知AC垂直平分BD,DF⊥BD,∠ABC=∠DCF.
(1)求证:四边形ACFD是平行四边形;
(2)若DF=CF=5,CD=6,求BD的长.
8.如图,在平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.
(1)求证:四边形AECF是平行四边形;
(2)若,∠ADE=30°,求四边形AECF的面积.
9.如图,在四边形ABCD中,对角线AC与BD交于点O,且AO=CO,AD∥BC.
(1)求证:四边形ABCD为平行四边形;
(2)若AB=10,OA=6,BD=16.
①求∠BOA的度数;
②求四边形ABCD的面积.
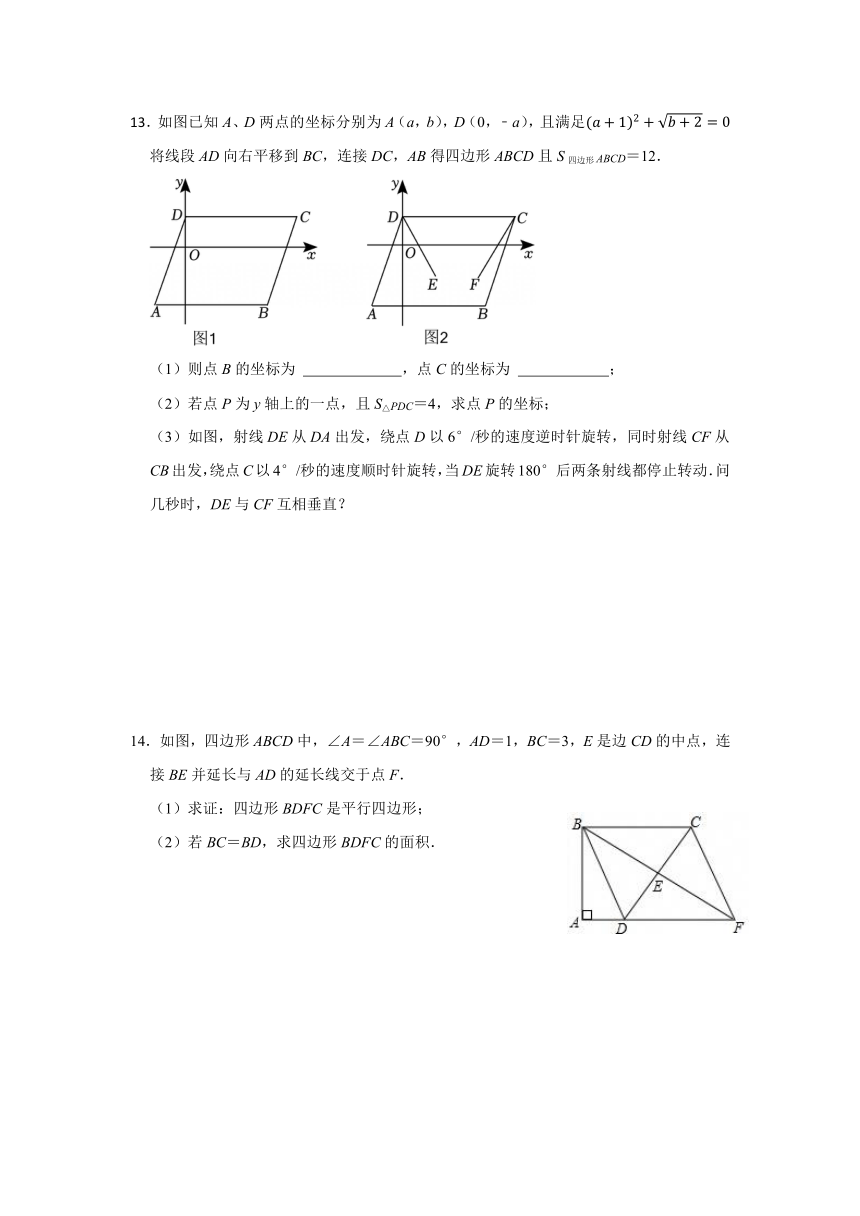
10.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.
11.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
12.如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:四边形AECF是平行四边形;
(2)若AD,AB=4,EF=3,试求四边形ABCD的面积.
13.如图已知A、D两点的坐标分别为A(a,b),D(0,﹣a),且满足将线段AD向右平移到BC,连接DC,AB得四边形ABCD且S四边形ABCD=12.
(1)则点B的坐标为 ,点C的坐标为 ;
(2)若点P为y轴上的一点,且S△PDC=4,求点P的坐标;
(3)如图,射线DE从DA出发,绕点D以6°/秒的速度逆时针旋转,同时射线CF从CB出发,绕点C以4°/秒的速度顺时针旋转,当DE旋转180°后两条射线都停止转动.问几秒时,DE与CF互相垂直?
14.如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若BC=BD,求四边形BDFC的面积.
15.如图1,E、F分别为平行四边形ABCD的边AB、DC上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)如图2,当DE平分∠ADC,AF⊥DC时,DF=3,AE=5,求平行四边形ABCD的面积.
16.△ABD,△ACE,△BCF,是分别以△ABC的AB、AC、BC边为一边的等边三角形.
(1)求证:四边形ADFE是平行四边形.
(2)若∠BAC=90°,AB=4,AC=3,求四边形的面积.
(3)试讨论△ABC的角满足什么条件时,四边形ADFE不存在.
17.如图, ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点.
(1)求证:四边形EFGH是平行四边形;
(2)若AC+BD=36,AB=12,求△OEF的周长.
18.如图:△ABD,△APE和△BPC均为直线AB同侧的等边三角形,点P在△ABD内.
(1)求证:四边形PEDC为平行四边形;
(2)当点P同时满足条件:①PA=PB和②∠APB=150°时,猜想四边形PEDC是什么特殊的四边形,并说明理由;
(3)若△APB中,,求四边形PEDC的面积.
19.如图,在四边形ABCD中,对角线AC与BD交于点O,且BO=DO,AD∥BC.
(1)求证:四边形ABCD为平行四边形;
(2)若AD=12,OD=5,AC=26.
①求∠ADB的度数;
②S四边形ABCD= .
参考答案
1.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=14,
∴OB=OD=7,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EGOB.
2.【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
∴△AED≌△CFB(AAS),
∴DE=BF.
(2)∵△ADE≌△CBF,
∴AE=CF,
∵∠AEF=∠CFE=90°,
∴AE∥CF,
∴四边形AFCE是平行四边形.
3.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADB=∠CBD.
∴∠ADE=∠CBF.
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
∴AE=CF,∠AED=∠CBF.
∴AE∥CF,
∴四边形AFCE是平行四边形;
(2)解:∵BD⊥AD,AB=5,BC=AD=3,
∴BD4,
连接AC交EF于O,如图,
∴DO=OBBD=2,
∵四边形AECF是平行四边形,
∴EO=OFEF,
∴DE=BF,
设DE=BF=x,
∴EF=2x+4,
∵EF﹣AF=2,
∴AF=2x+2,
∵AF2=AD2+DF2,
∴(2x+2)2=32+(4+x)2,
∴x(负值舍去),
∴DE的长为.
4.【解答】(1)证明:∵AD∥BC.,
∴∠DAO=∠BCO,
在△ADO和△CBO中,
,
∴△ADO≌△CBO(ASA),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:①∵OA=6,OB=8,AB=10,OBBD=8,
∴OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠BOA=90°;
②由①可知,AC垂直平分BD,
∴AB=AD,
∴四边形ABCD是菱形,
∴AC=2OA=12,
∴S四边形ABCDAC BD12×16=96.
5.【解答】证明:∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠DAB=∠BCD.
又∵△ADE和△CBF都是等边三角形,
∴DE=BF,AE=CF.
∠DAE=∠BCF=60°.
∵∠DCF=∠BCD﹣∠BCF,
∠BAE=∠DAB﹣∠DAE,
∴∠DCF=∠BAE.
∴△DCF≌△BAE(SAS).
∴DF=BE.
∴四边形BEDF是平行四边形.
6.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠DAE=∠C,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(AAS),
∴AE=CF,
∴DF=BE,
∵DF∥BE,
∴四边形DEBF为平行四边形;
(2)解:∵AF平分∠BAD,
∴∠DAF=∠BAF,
∵AB∥CD,
∴∠AFD=∠BAF,
∴∠DAF=∠AFD,
∴AD=DF,
∵DF=BE,
∴BE=6,
∵DE⊥AB,BF∥DE,
∴BF⊥AB,
∴∠AHD=∠ABF=90°,
∵四边形DEBF为平行四边形,
∴DE=BF,
∵AD2﹣AE2=DE2,AF2﹣AB2=BF2,
∴AD2﹣AE2=AF2﹣AB2,
∴62﹣AE2=102﹣(AE+6)2,
∴AE.
7.【解答】(1)证明:∵AC垂直平分BD,
∴AB=AD,BC=DC,
在△ABC与△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC,
∵∠ABC=∠DCF,
∴∠ADC=∠DCF,
∴AD∥CF,
∵AC⊥BD,DF⊥BD,
∴DF∥AC,
∴四边形ACFD是平行四边形;
(2)解:∵四边形ACDF是平行四边形,DF=CF=5,
∴ ACDF是菱形,
∴AD=5,
设CE=x,则AE=5﹣x,
∴CD2﹣CE2=AD2﹣AE2
即62﹣x2=52﹣(5﹣x)2
解得:x=3.6,即CE=3.6,
∴DE,
∴BD=2DE=9.6.
8.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形;
(2)解:∵AE⊥BD,
∴∠AED=90°,
∵∠ADE=30°,AD=8,
∴AEAD=4,
∴DE4,
由(1)可知,△ABE≌△CDF,
∴DF=BE=2,
∴EF=DE﹣DF=422,
∵四边形AECF是平行四边形,AE⊥EF,
∴S平行四边形AECF=AE EF=4×28.
9.【解答】(1)证明:∵AD∥BC,
∴∠DAO=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴OB=OD,
∵OA=OC,
∴四边形ABCD为平行四边形;
(2)解:①∵BD=16,
OB=OD=8,
∵AB=10,OA=6,
∴AB2=OA2+OB2,
∴△AOB是直角三角形,
∴∠BOA=90°;
②由①可知,∠BOA=90°,
∴BD⊥AC,
∵OA=6,
∴AC=12,
∴S四边形ABCDBD AC16×12=96.
10.【解答】(1)证明:∵AD∥BC,
∴∠OAD=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=CB,
又∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:设∠ABE=x,则∠DBF=2x,
由(1)得:四边形ABCD为平行四边形,
∴OB=OD,
∵EF⊥BD,
∴BE=DE,
∴∠EBD=∠EDB,
∵AD∥BC,
∴∠EDB=∠DBF,
∴∠EBD=∠EDB=∠DBF=2x,
∵∠BAD+∠ABE+∠EBD+∠EDB=180°,
∴100°+x+2x+2x=180°,
解得:x=16°,
即∠ABE=16°.
11.【解答】(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OD=OE,
又∵AO=CO,
∴四边形AECD是平行四边形;
(2)解:∵AB=BC,AO=CO,
∴OB⊥AC,
∴平行四边形AECD是菱形,
∵AC=8,
∴COAC=4,
在Rt△COD中,由勾股定理得:OD3,
∴DE=2OD=6,
∴菱形AECD的面积AC×DE8×6=24.
12.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF,
又∵AE∥CF,
∴四边形AECF是平行四边形;
(2)解:由(1)可知,△ABE≌△CDF,
∴BE=DF,
∴BE﹣EF=DF﹣EF,
即BF=DE,
设BF=DE=x,则BE=BF+EF=x+3,BD=2x+3,
∵AE⊥BD,
∴∠AED=∠AEB=90°,
在Rt△ADE和Rt△ABE中,由勾股定理得:AE2=AD2﹣DE2,AE2=AB2﹣BE2,
∴AD2﹣DE2=AB2﹣BE2,
即()2﹣x2=(4)2﹣(x+3)2,
解得:x=1,
∴BD=2x+3=2+3=5,AE4,
∵四边形ABCD是平行四边形,
∴S平行四边形ABCD=2S△ABD=2BD AE=BD AE=5×4=20.
13.【解答】解:(1)∵,
∴a+1=0,b+2=0,
解得:a=﹣1,b=﹣2,
∴A(﹣1,﹣2),D(0,1),
∴DH=1﹣(﹣2)=3,
∵线段AD向右平移到BC,
∴AD∥BC,AD=BC,
∴四边形ABCD为平行四边形,
∴AB×DH=12,
解得:AB=4,
∴DC=AB=4,
∴B(3,﹣2),C(4,1).
故答案为:(3,﹣2);(4,1).
(2)解:设点P的坐标为(0,m),
∵S△PDC=4,
∴,
解得:m=3或m=﹣1,
∴点P的坐标为:(0,3)或(0,﹣1).
(3)设运动时间为t秒,则∠ADE=6t,∠BCF=4t,
第一次DE⊥CF时,如图所示:
则∠CGD=90°,
∴∠CDG+∠DCG=90°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADG+∠BCG=180°﹣(∠CDG+∠DCG)=90°,
∴6t+4t=90°,
解得:t=9;
第二次DE⊥CF时,如图所示:
则∠CGD=90°,
∴∠CDG+∠DCG=90°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADG+∠BCG=180°+(∠CDG+∠DCG)=270°,
∴6t+4t=270°,
解得:t=27,
综上分析可知,当9秒或27秒时,DE与CF互相垂直.
14.【解答】(1)证明:∵∠A=∠ABC=90°,
∴∠A+∠ABC=180°,
∴BC∥AD,
∴∠CBE=∠DFE,
又∵E是边CD的中点,
∴CE=DE,
在△BEC与△FED中,
,
∴△BEC≌△FED(AAS),
∴BE=FE,
∴四边形BDFC是平行四边形;
(2)解:∵BD=BC=3,∠A=90°,
∴AB2,
由(1)得:四边形BDFC是平行四边形,
∴平行四边形BDFC的面积=BC AB=3×26.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵BE=DF,
∴AB﹣BE=CD﹣DF,
即AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形;
(2)解:∵AB∥CD,
∴∠AED=∠CDE,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠AED=∠ADE,
∴AD=AE=5,
由(1)可知,四边形AECF是平行四边形,
∴FC=AE=5,
∴CD=DF+FC=3+5=8,
∵AF⊥DC,
∴∠AFD=90°,
∴AF4,
∴S平行四边形ABCD=CD AF=8×4=32.
16.【解答】(1)证明:四边形ADEF是平行四边形.
∵等边三角形BCF和等边三角形ABD,
∴BE=BC,BD=BA.
又∵∠DBE=60°﹣∠ABF,∠ABC=60°﹣∠ABF,
∴∠DBE=∠ABC.
在△BDF和△BCA中,
,
∴△BDF≌△BCA(SAS).
∴DF=AC.
∵在等边三角形ACF中,AC=AE,
∴DF=AE.
同理DA=EF.
∴四边形ADEF是平行四边形;
(2)解:∵∠BAC=90°,AB=4,AC=3,
∴BC=5,
∵∠BAC=90°,
又∵∠DAB=∠EAC=60°,
∴∠DAE=360°﹣90°﹣60°﹣60°=150°,
∴∠FDA=30°,
如图,过F作FM⊥AD于点M,
则可知FMFDAEAC=1.5,
且AD=AB=4,
∴S四边形ADEF=AD FM=4×1.5=6.
(3)当D,A,E三点共线时,四边形ADFE不存在,
当∠BAC=60°时,四边形ADFE不存在,
此时,∠DAE=360°﹣∠DAB﹣∠BAC﹣∠CAE=360°﹣60°﹣60°﹣60°=180°,
此时D,A,E三点共线,
当△ABC中∠BAC=60°时,四边形ADFE不存在.
17.【解答】证明:(1)∵四边形ABCD是平行四边形
∴AO=CO,BO=DO,
∵E、F、G、H分别是AO、BO、CO、DO的中点.
∴EOAO,GOCO,FOBO,HODO
∴EO=GO,FO=HO
∴四边形EFGH是平行四边形;
(2)∵AC+BD=36,
∴AO+BO=18,
∴EO+FO=9
∵E、F分别是AO、BO的中点,
∴EFAB,且AB=12
∴EF=6,
∴△OEF的周长=OE+OF+EF=9+6=15
18.【解答】(1)证明:∵△AEP,△DAB是等边三角形,
∴AE=AP,AD=AB,∠EAP=∠DAB=60°,
∴∠EAD=∠PAB,
∴△EAD≌△PAB(SAS),
∴DE=BP,
∵PC=PB,
∴DE=PC,
同理PE=CD,
∴四边形PEDC是平行四边形;
(2)解:此时四边形PEDC为正方形.
理由:当PA=PB时,
∵PE=PA,PC=PB,
∴PE=PC,
∵四边形PEDC是平行四边形,
∴四边形PEDC是菱形.
当∠APB=150°时,∵∠APE=∠BPC=60°,
∴∠EPC=360°﹣60°﹣60°﹣150°=90°,
又∵四边形PEDC是菱形,
∴四边形PEDC是正方形.
(3)解;如图所示,过C作CH垂直EP的延长线于H,
∵AB=3,PA,PB=2,
∴PA2+PB2=AB2,
∴∠APB=90°
又∵∠APE=∠BPC=60°,
∴∠EPC=150°,
∴∠CPH=30°,
∵∠PHC=90°,
∴CHCPPB=1,
又PE=PA,
∴S平行四边形PEDC=CH×EP=1.
19.【解答】(1)证明:∵AD∥BC,
∴∠ADO=∠CBO,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:①∵四边形ABCD为平行四边形,AC=26,
∴OA=OC=13,
∵AD=12,OD=5,
∴AD2+OD2=OA2,
∴△AOD是直角三角形,∠ADO=90°,
即∠ADB=90°;
②由①可知,∠ADB=90°,
∴BD⊥AD,
∵四边形ABCD是平行四边形,
∴BD=2OD=10,
∴S四边形ABCD=AD BD=12×10=120,
故答案为:120.
1.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
2.如图,在 ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.求证:
(1)DE=BF;
(2)四边形AFCE是平行四边形.
3.已知:如图,在 ABCD中,E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AECF是平行四边形;
(2)若AD⊥BD,AB=5,AD=3,且EF﹣AF=2,求DE的长.
4.如图,在四边形ABCD中,对角线AC与BD相交于点O,且AO=CO,AD∥BC.
(1)求证:四边形ABCD为平行四边形;
(2)若AB=10,OA=6,BD=16.
①求∠BOA的度数;
②求四边形ABCD的面积.
5.在平行四边形ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.
6.如图,在 ABCD中,E,F两点分别在边AB,CD上,连接DE,BF,AF,且∠ADE=∠CBF.
(1)求证:四边形DEBF为平行四边形;
(2)若AF平分∠BAD,DE⊥AB,且AD=6,AF=10,求AE的长.
7.如图,已知AC垂直平分BD,DF⊥BD,∠ABC=∠DCF.
(1)求证:四边形ACFD是平行四边形;
(2)若DF=CF=5,CD=6,求BD的长.
8.如图,在平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.
(1)求证:四边形AECF是平行四边形;
(2)若,∠ADE=30°,求四边形AECF的面积.
9.如图,在四边形ABCD中,对角线AC与BD交于点O,且AO=CO,AD∥BC.
(1)求证:四边形ABCD为平行四边形;
(2)若AB=10,OA=6,BD=16.
①求∠BOA的度数;
②求四边形ABCD的面积.
10.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.
11.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
12.如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:四边形AECF是平行四边形;
(2)若AD,AB=4,EF=3,试求四边形ABCD的面积.
13.如图已知A、D两点的坐标分别为A(a,b),D(0,﹣a),且满足将线段AD向右平移到BC,连接DC,AB得四边形ABCD且S四边形ABCD=12.
(1)则点B的坐标为 ,点C的坐标为 ;
(2)若点P为y轴上的一点,且S△PDC=4,求点P的坐标;
(3)如图,射线DE从DA出发,绕点D以6°/秒的速度逆时针旋转,同时射线CF从CB出发,绕点C以4°/秒的速度顺时针旋转,当DE旋转180°后两条射线都停止转动.问几秒时,DE与CF互相垂直?
14.如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若BC=BD,求四边形BDFC的面积.
15.如图1,E、F分别为平行四边形ABCD的边AB、DC上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)如图2,当DE平分∠ADC,AF⊥DC时,DF=3,AE=5,求平行四边形ABCD的面积.
16.△ABD,△ACE,△BCF,是分别以△ABC的AB、AC、BC边为一边的等边三角形.
(1)求证:四边形ADFE是平行四边形.
(2)若∠BAC=90°,AB=4,AC=3,求四边形的面积.
(3)试讨论△ABC的角满足什么条件时,四边形ADFE不存在.
17.如图, ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点.
(1)求证:四边形EFGH是平行四边形;
(2)若AC+BD=36,AB=12,求△OEF的周长.
18.如图:△ABD,△APE和△BPC均为直线AB同侧的等边三角形,点P在△ABD内.
(1)求证:四边形PEDC为平行四边形;
(2)当点P同时满足条件:①PA=PB和②∠APB=150°时,猜想四边形PEDC是什么特殊的四边形,并说明理由;
(3)若△APB中,,求四边形PEDC的面积.
19.如图,在四边形ABCD中,对角线AC与BD交于点O,且BO=DO,AD∥BC.
(1)求证:四边形ABCD为平行四边形;
(2)若AD=12,OD=5,AC=26.
①求∠ADB的度数;
②S四边形ABCD= .
参考答案
1.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=14,
∴OB=OD=7,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EGOB.
2.【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
∴△AED≌△CFB(AAS),
∴DE=BF.
(2)∵△ADE≌△CBF,
∴AE=CF,
∵∠AEF=∠CFE=90°,
∴AE∥CF,
∴四边形AFCE是平行四边形.
3.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADB=∠CBD.
∴∠ADE=∠CBF.
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
∴AE=CF,∠AED=∠CBF.
∴AE∥CF,
∴四边形AFCE是平行四边形;
(2)解:∵BD⊥AD,AB=5,BC=AD=3,
∴BD4,
连接AC交EF于O,如图,
∴DO=OBBD=2,
∵四边形AECF是平行四边形,
∴EO=OFEF,
∴DE=BF,
设DE=BF=x,
∴EF=2x+4,
∵EF﹣AF=2,
∴AF=2x+2,
∵AF2=AD2+DF2,
∴(2x+2)2=32+(4+x)2,
∴x(负值舍去),
∴DE的长为.
4.【解答】(1)证明:∵AD∥BC.,
∴∠DAO=∠BCO,
在△ADO和△CBO中,
,
∴△ADO≌△CBO(ASA),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:①∵OA=6,OB=8,AB=10,OBBD=8,
∴OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠BOA=90°;
②由①可知,AC垂直平分BD,
∴AB=AD,
∴四边形ABCD是菱形,
∴AC=2OA=12,
∴S四边形ABCDAC BD12×16=96.
5.【解答】证明:∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠DAB=∠BCD.
又∵△ADE和△CBF都是等边三角形,
∴DE=BF,AE=CF.
∠DAE=∠BCF=60°.
∵∠DCF=∠BCD﹣∠BCF,
∠BAE=∠DAB﹣∠DAE,
∴∠DCF=∠BAE.
∴△DCF≌△BAE(SAS).
∴DF=BE.
∴四边形BEDF是平行四边形.
6.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠DAE=∠C,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(AAS),
∴AE=CF,
∴DF=BE,
∵DF∥BE,
∴四边形DEBF为平行四边形;
(2)解:∵AF平分∠BAD,
∴∠DAF=∠BAF,
∵AB∥CD,
∴∠AFD=∠BAF,
∴∠DAF=∠AFD,
∴AD=DF,
∵DF=BE,
∴BE=6,
∵DE⊥AB,BF∥DE,
∴BF⊥AB,
∴∠AHD=∠ABF=90°,
∵四边形DEBF为平行四边形,
∴DE=BF,
∵AD2﹣AE2=DE2,AF2﹣AB2=BF2,
∴AD2﹣AE2=AF2﹣AB2,
∴62﹣AE2=102﹣(AE+6)2,
∴AE.
7.【解答】(1)证明:∵AC垂直平分BD,
∴AB=AD,BC=DC,
在△ABC与△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC,
∵∠ABC=∠DCF,
∴∠ADC=∠DCF,
∴AD∥CF,
∵AC⊥BD,DF⊥BD,
∴DF∥AC,
∴四边形ACFD是平行四边形;
(2)解:∵四边形ACDF是平行四边形,DF=CF=5,
∴ ACDF是菱形,
∴AD=5,
设CE=x,则AE=5﹣x,
∴CD2﹣CE2=AD2﹣AE2
即62﹣x2=52﹣(5﹣x)2
解得:x=3.6,即CE=3.6,
∴DE,
∴BD=2DE=9.6.
8.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形;
(2)解:∵AE⊥BD,
∴∠AED=90°,
∵∠ADE=30°,AD=8,
∴AEAD=4,
∴DE4,
由(1)可知,△ABE≌△CDF,
∴DF=BE=2,
∴EF=DE﹣DF=422,
∵四边形AECF是平行四边形,AE⊥EF,
∴S平行四边形AECF=AE EF=4×28.
9.【解答】(1)证明:∵AD∥BC,
∴∠DAO=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴OB=OD,
∵OA=OC,
∴四边形ABCD为平行四边形;
(2)解:①∵BD=16,
OB=OD=8,
∵AB=10,OA=6,
∴AB2=OA2+OB2,
∴△AOB是直角三角形,
∴∠BOA=90°;
②由①可知,∠BOA=90°,
∴BD⊥AC,
∵OA=6,
∴AC=12,
∴S四边形ABCDBD AC16×12=96.
10.【解答】(1)证明:∵AD∥BC,
∴∠OAD=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=CB,
又∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:设∠ABE=x,则∠DBF=2x,
由(1)得:四边形ABCD为平行四边形,
∴OB=OD,
∵EF⊥BD,
∴BE=DE,
∴∠EBD=∠EDB,
∵AD∥BC,
∴∠EDB=∠DBF,
∴∠EBD=∠EDB=∠DBF=2x,
∵∠BAD+∠ABE+∠EBD+∠EDB=180°,
∴100°+x+2x+2x=180°,
解得:x=16°,
即∠ABE=16°.
11.【解答】(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OD=OE,
又∵AO=CO,
∴四边形AECD是平行四边形;
(2)解:∵AB=BC,AO=CO,
∴OB⊥AC,
∴平行四边形AECD是菱形,
∵AC=8,
∴COAC=4,
在Rt△COD中,由勾股定理得:OD3,
∴DE=2OD=6,
∴菱形AECD的面积AC×DE8×6=24.
12.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF,
又∵AE∥CF,
∴四边形AECF是平行四边形;
(2)解:由(1)可知,△ABE≌△CDF,
∴BE=DF,
∴BE﹣EF=DF﹣EF,
即BF=DE,
设BF=DE=x,则BE=BF+EF=x+3,BD=2x+3,
∵AE⊥BD,
∴∠AED=∠AEB=90°,
在Rt△ADE和Rt△ABE中,由勾股定理得:AE2=AD2﹣DE2,AE2=AB2﹣BE2,
∴AD2﹣DE2=AB2﹣BE2,
即()2﹣x2=(4)2﹣(x+3)2,
解得:x=1,
∴BD=2x+3=2+3=5,AE4,
∵四边形ABCD是平行四边形,
∴S平行四边形ABCD=2S△ABD=2BD AE=BD AE=5×4=20.
13.【解答】解:(1)∵,
∴a+1=0,b+2=0,
解得:a=﹣1,b=﹣2,
∴A(﹣1,﹣2),D(0,1),
∴DH=1﹣(﹣2)=3,
∵线段AD向右平移到BC,
∴AD∥BC,AD=BC,
∴四边形ABCD为平行四边形,
∴AB×DH=12,
解得:AB=4,
∴DC=AB=4,
∴B(3,﹣2),C(4,1).
故答案为:(3,﹣2);(4,1).
(2)解:设点P的坐标为(0,m),
∵S△PDC=4,
∴,
解得:m=3或m=﹣1,
∴点P的坐标为:(0,3)或(0,﹣1).
(3)设运动时间为t秒,则∠ADE=6t,∠BCF=4t,
第一次DE⊥CF时,如图所示:
则∠CGD=90°,
∴∠CDG+∠DCG=90°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADG+∠BCG=180°﹣(∠CDG+∠DCG)=90°,
∴6t+4t=90°,
解得:t=9;
第二次DE⊥CF时,如图所示:
则∠CGD=90°,
∴∠CDG+∠DCG=90°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADG+∠BCG=180°+(∠CDG+∠DCG)=270°,
∴6t+4t=270°,
解得:t=27,
综上分析可知,当9秒或27秒时,DE与CF互相垂直.
14.【解答】(1)证明:∵∠A=∠ABC=90°,
∴∠A+∠ABC=180°,
∴BC∥AD,
∴∠CBE=∠DFE,
又∵E是边CD的中点,
∴CE=DE,
在△BEC与△FED中,
,
∴△BEC≌△FED(AAS),
∴BE=FE,
∴四边形BDFC是平行四边形;
(2)解:∵BD=BC=3,∠A=90°,
∴AB2,
由(1)得:四边形BDFC是平行四边形,
∴平行四边形BDFC的面积=BC AB=3×26.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵BE=DF,
∴AB﹣BE=CD﹣DF,
即AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形;
(2)解:∵AB∥CD,
∴∠AED=∠CDE,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠AED=∠ADE,
∴AD=AE=5,
由(1)可知,四边形AECF是平行四边形,
∴FC=AE=5,
∴CD=DF+FC=3+5=8,
∵AF⊥DC,
∴∠AFD=90°,
∴AF4,
∴S平行四边形ABCD=CD AF=8×4=32.
16.【解答】(1)证明:四边形ADEF是平行四边形.
∵等边三角形BCF和等边三角形ABD,
∴BE=BC,BD=BA.
又∵∠DBE=60°﹣∠ABF,∠ABC=60°﹣∠ABF,
∴∠DBE=∠ABC.
在△BDF和△BCA中,
,
∴△BDF≌△BCA(SAS).
∴DF=AC.
∵在等边三角形ACF中,AC=AE,
∴DF=AE.
同理DA=EF.
∴四边形ADEF是平行四边形;
(2)解:∵∠BAC=90°,AB=4,AC=3,
∴BC=5,
∵∠BAC=90°,
又∵∠DAB=∠EAC=60°,
∴∠DAE=360°﹣90°﹣60°﹣60°=150°,
∴∠FDA=30°,
如图,过F作FM⊥AD于点M,
则可知FMFDAEAC=1.5,
且AD=AB=4,
∴S四边形ADEF=AD FM=4×1.5=6.
(3)当D,A,E三点共线时,四边形ADFE不存在,
当∠BAC=60°时,四边形ADFE不存在,
此时,∠DAE=360°﹣∠DAB﹣∠BAC﹣∠CAE=360°﹣60°﹣60°﹣60°=180°,
此时D,A,E三点共线,
当△ABC中∠BAC=60°时,四边形ADFE不存在.
17.【解答】证明:(1)∵四边形ABCD是平行四边形
∴AO=CO,BO=DO,
∵E、F、G、H分别是AO、BO、CO、DO的中点.
∴EOAO,GOCO,FOBO,HODO
∴EO=GO,FO=HO
∴四边形EFGH是平行四边形;
(2)∵AC+BD=36,
∴AO+BO=18,
∴EO+FO=9
∵E、F分别是AO、BO的中点,
∴EFAB,且AB=12
∴EF=6,
∴△OEF的周长=OE+OF+EF=9+6=15
18.【解答】(1)证明:∵△AEP,△DAB是等边三角形,
∴AE=AP,AD=AB,∠EAP=∠DAB=60°,
∴∠EAD=∠PAB,
∴△EAD≌△PAB(SAS),
∴DE=BP,
∵PC=PB,
∴DE=PC,
同理PE=CD,
∴四边形PEDC是平行四边形;
(2)解:此时四边形PEDC为正方形.
理由:当PA=PB时,
∵PE=PA,PC=PB,
∴PE=PC,
∵四边形PEDC是平行四边形,
∴四边形PEDC是菱形.
当∠APB=150°时,∵∠APE=∠BPC=60°,
∴∠EPC=360°﹣60°﹣60°﹣150°=90°,
又∵四边形PEDC是菱形,
∴四边形PEDC是正方形.
(3)解;如图所示,过C作CH垂直EP的延长线于H,
∵AB=3,PA,PB=2,
∴PA2+PB2=AB2,
∴∠APB=90°
又∵∠APE=∠BPC=60°,
∴∠EPC=150°,
∴∠CPH=30°,
∵∠PHC=90°,
∴CHCPPB=1,
又PE=PA,
∴S平行四边形PEDC=CH×EP=1.
19.【解答】(1)证明:∵AD∥BC,
∴∠ADO=∠CBO,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:①∵四边形ABCD为平行四边形,AC=26,
∴OA=OC=13,
∵AD=12,OD=5,
∴AD2+OD2=OA2,
∴△AOD是直角三角形,∠ADO=90°,
即∠ADB=90°;
②由①可知,∠ADB=90°,
∴BD⊥AD,
∵四边形ABCD是平行四边形,
∴BD=2OD=10,
∴S四边形ABCD=AD BD=12×10=120,
故答案为:120.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
