6.3三角形的中位线培优练习(含解析)
文档属性
| 名称 | 6.3三角形的中位线培优练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 17:00:56 | ||
图片预览


文档简介
6.3三角形的中位线培优练习北师大版2024—2025学年八年级下册
一.选择题(共6小题)
1.如图,△ABC的周长为20,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=8,则MN的长度为( )
A. B.2 C. D.3
2.如图,△ABC中,AB=8,AD为∠BAC的外角平分线,且AD⊥CD于点D,E为BC的中点,若DE=10,则AC的长为( )
A.12 B.14 C.16 D.18
3.如图,点D为△ABC中BC边中点,E为AD中点,BE交AC于F,若AB=4,EF=1,,则AD的长为( )
A.3 B. C.4 D.
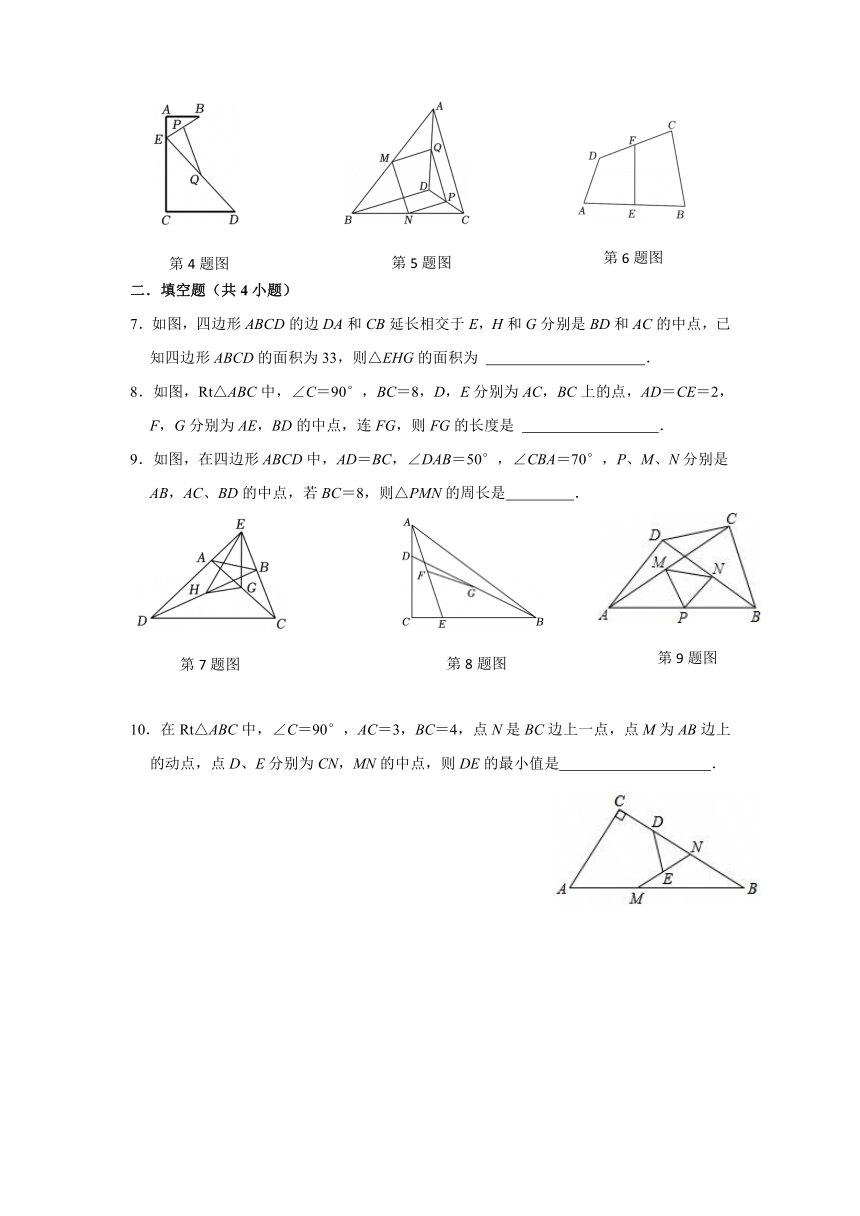
4.如图,AC是带有滑道的铁杠,AB,CD是两段横木,E是部分嵌在滑道里的可以滑动的螺钉,BE,DE,PQ是三段橡皮筋,其中,P,Q分别是BE,DE的中点,螺钉E在滑道AC内上下滑动时,橡皮筋PQ的长度( )
A.螺钉E滑至AC两端处时,PQ的长度最大
B.螺钉E滑至AC中点处时,PQ的长度最大
C.上下滑动时,PQ的长度时而增大时而减小
D.上下滑动时,PQ的长度始终不变
5.如图,D是△ABC内部一点,AC⊥BD,且,依次取AB,BC,CD,AD的中点,并顺次连接得到四边形MNPQ,则四边形MNPQ的面积是( )
A.6 B.12 C.24 D.48
6.如图,四边形ABCD中,点E,F分别是边AB,CD的中点,且AD=6,BC=10,则线段EF的长可能为( )
A.7 B.8.5 C.9 D.10
二.填空题(共4小题)
7.如图,四边形ABCD的边DA和CB延长相交于E,H和G分别是BD和AC的中点,已知四边形ABCD的面积为33,则△EHG的面积为 .
8.如图,Rt△ABC中,∠C=90°,BC=8,D,E分别为AC,BC上的点,AD=CE=2,F,G分别为AE,BD的中点,连FG,则FG的长度是 .
9.如图,在四边形ABCD中,AD=BC,∠DAB=50°,∠CBA=70°,P、M、N分别是AB,AC、BD的中点,若BC=8,则△PMN的周长是 .
10.在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是 .
三.填空题(共10小题)
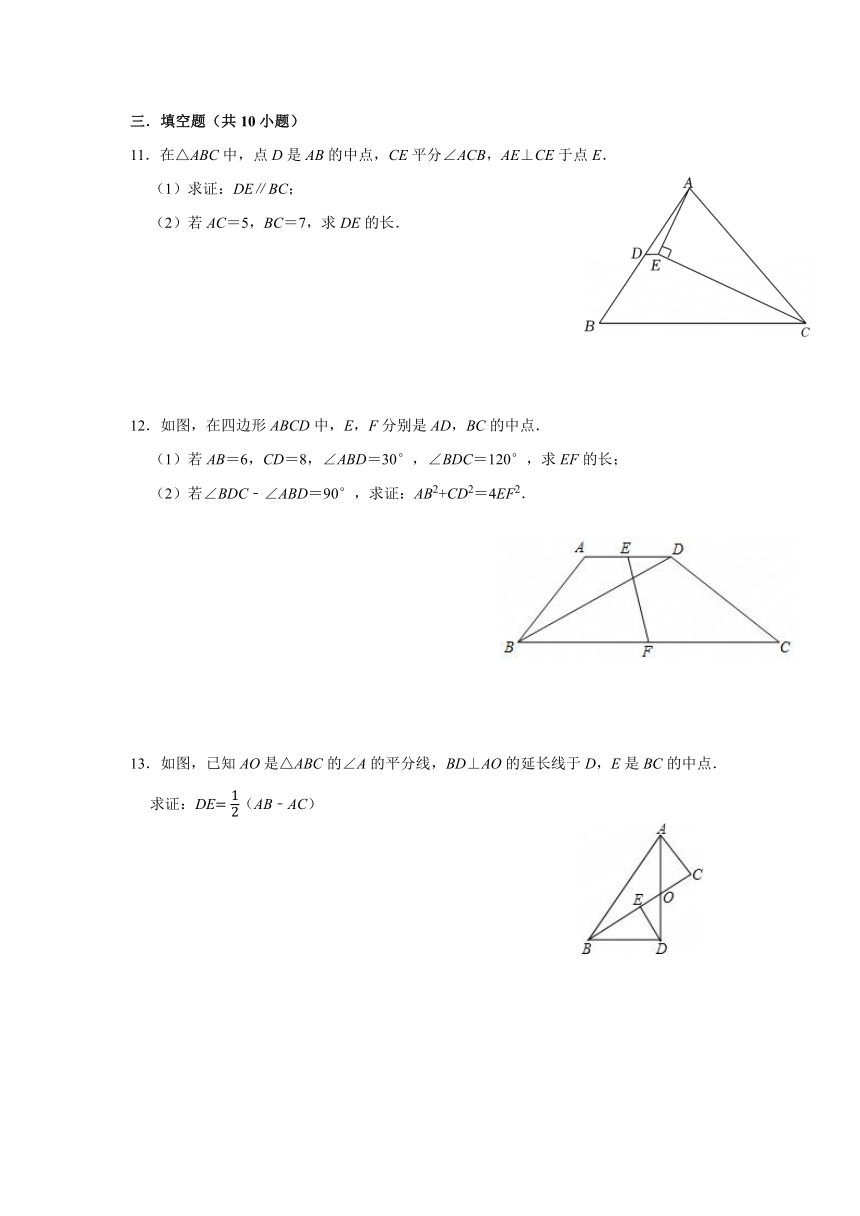
11.在△ABC中,点D是AB的中点,CE平分∠ACB,AE⊥CE于点E.
(1)求证:DE∥BC;
(2)若AC=5,BC=7,求DE的长.
12.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
13.如图,已知AO是△ABC的∠A的平分线,BD⊥AO的延长线于D,E是BC的中点.
求证:DE(AB﹣AC)
14.(1)如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.
求证:∠BME=∠CNE;(提示:取BD的中点H,连接FH,HE作辅助线)
(2)如图2,在△ABC中,F是BC边的中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=45°,求FE的长度.
15.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
16.如图所示.△ABC中,∠B,∠C的平分线BE,CF相交于O,AG⊥BE于G,AH⊥CF于H.
(1)求证:GH∥BC;
(2)若AB=9厘米,AC=14厘米,BC=18厘米,求GH.
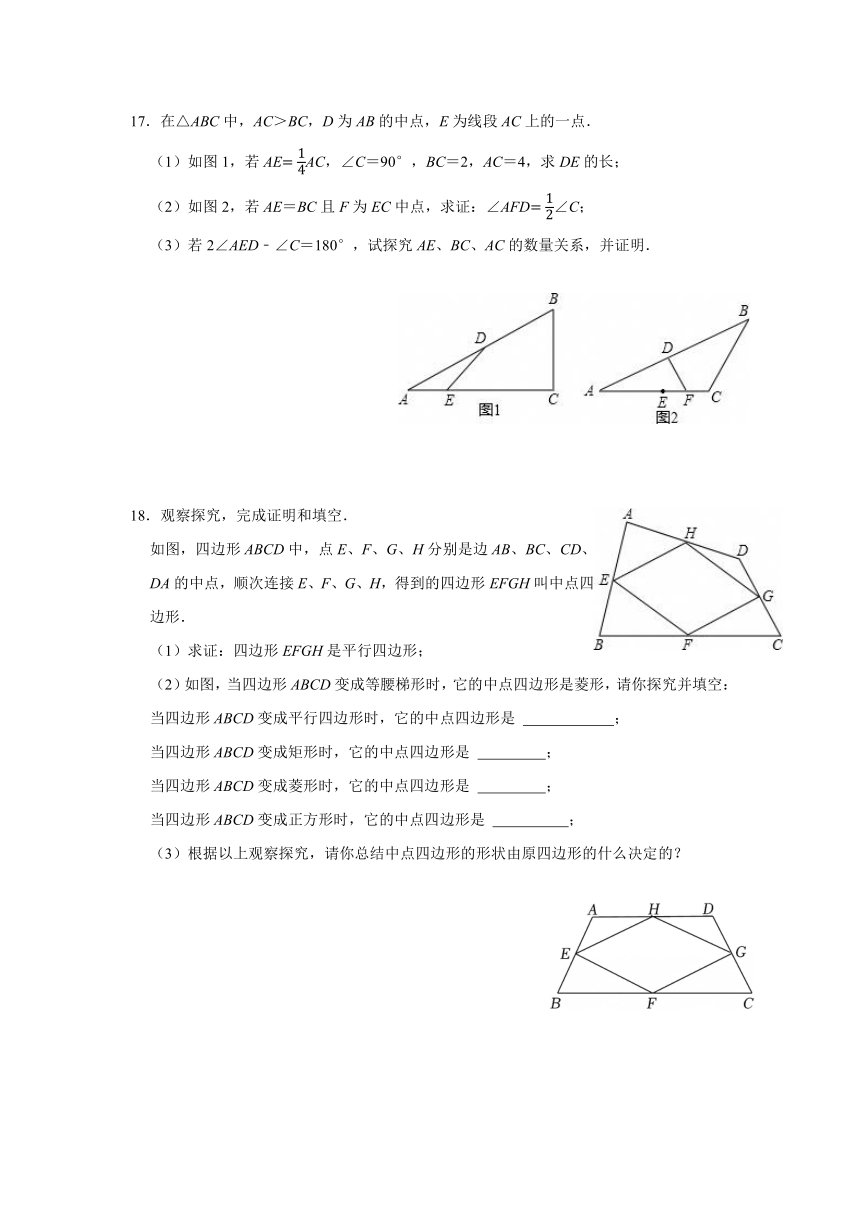
17.在△ABC中,AC>BC,D为AB的中点,E为线段AC上的一点.
(1)如图1,若AEAC,∠C=90°,BC=2,AC=4,求DE的长;
(2)如图2,若AE=BC且F为EC中点,求证:∠AFD∠C;
(3)若2∠AED﹣∠C=180°,试探究AE、BC、AC的数量关系,并证明.
18.观察探究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 ;
当四边形ABCD变成矩形时,它的中点四边形是 ;
当四边形ABCD变成菱形时,它的中点四边形是 ;
当四边形ABCD变成正方形时,它的中点四边形是 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
19.如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.
(1)求证:CD∥AB;
(2)求证:△BDE≌△ACE;
(3)若O为AB中点,求证:OFBE.
20.如图,△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
(1)求证:DM(AC﹣AB);
(2)若AD=6,BD=8,DM=2,求AC的长.
参考答案
1.B.2.A.3.C.4.D.5.B.
6.【解答】解:连接BD,取BD的中点H,连接HF、HE,
∵点E,H分别是边AB,BD的中点,
∴EH是△ABD的中位线,
∴EHAD=3,
同理可得:FHBC=5,
∴FH﹣EH≤EF≤FH+EH,即2≤EF≤8,
故选:A.
7.【解答】解:连接AH,CH,BG,如图:
设S△AHG=S△HGC=m,S△ABG=S△BGC=n,
∵S△ADH=S△AHB,S△DHC=S△BHC,
∴S△ADH+S△DHC=S△AHB+S△BHC=2m+2n,
∴S四边形ABCD=2(S△ADH+S△DHC)=4m+4n,
∴,
设S△ABE=x,则,
∴.
故答案为:.
8.【解答】解:如图,取AB的中点H,连接HF,HG并延长交AC于点I,交BC于点J,
∵F,G分别为AE,BD的中点,
∴HG是△ABD的中位线,HF是△AEB的中位线,
∴HG,HG∥AC,HF,HF∥BC,
∴四边形IHJC是平行四边形,
∵∠C=90°,
∴四边形IHJC是矩形,
∴∠FHG=90°,
∴FG,
故答案为:.
9.【解答】解:∵P、N是AB和BD的中点,
∴PNAD8=4,PN∥AD,
∴∠NPB=∠DAB=50°,
同理,PM=4,∠MPA=∠CBA=70°,
∴PM=PN=4,∠MPN=180°﹣50°﹣70°=60°,
∴△PMN是等边三角形.
∴MN=PM=PN=4,
∴△PMN的周长是12.
10.【解答】解:连接CM,
∵点D、E分别为CN,MN的中点,
∴DECM,
当CM⊥AB时,CM的值最小,此时DE的值也最小,
由勾股定理得:AB5,
∵S△ABC,
∴CM,
∴DE,
故答案为:.
11.在△ABC中,点D是AB的中点,CE平分∠ACB,AE⊥CE于点E.
(1)求证:DE∥BC;
(2)若AC=5,BC=7,求DE的长.
【解答】解:(1)延长AE交BC于F,
∵CE平分∠ACB,AE⊥CE于点E,
∴∠ACE=∠FCE,∠AEC=∠FEC=90°,
在△ACE和△FCE中,
,
∴△ACE≌△FCE.
∴AE=EF,
∵点D是AB的中点,
∴AD=BD,
∴DE是△ABF的中位线.
∴DE∥BC;
(2)∵△ACE≌△FCE,
∴CF=AC=5,
∵DE是△ABF的中位线.
∴DEBF(BC﹣AC)(7﹣5)=1,
故DE的长为1.
12.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
【解答】(1)解:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,AB=6,CD=8,
∴PE是△ADB的中位线,
∴PE∥AB,且PEAB=3,PF∥CD且PFCD=4.
又∵∠ABD=30°,∠BDC=120°,
∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在直角△EPF中,由勾股定理得到:EF5,
即EF=5;
(2)证明:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,
∴PE∥AB,且PEAB,PF∥CD且PFCD.
∴∠EPD=∠ABD,∠BPF=∠BDC,
∴∠DPF=180°﹣∠BPF=180°﹣∠BDC,
∵∠BDC﹣∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,
∴PE2+PF2=(AB)2+(CD)2=EF2,
∴AB2+CD2=4EF2.
13.如图,已知AO是△ABC的∠A的平分线,BD⊥AO的延长线于D,E是BC的中点.
求证:DE(AB﹣AC)
【解答】证明:延长AC、BD交于点F,
∵在△ABD和△AFD中,
,
∴△ABD≌△AFD(ASA),
∴AB=AF,BD=DF,
又∵E是BC的中点,即ED是△BCF中位线,
∴DECF(AB﹣AC).
14.(1)如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.
求证:∠BME=∠CNE;(提示:取BD的中点H,连接FH,HE作辅助线)
(2)如图2,在△ABC中,F是BC边的中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=45°,求FE的长度.
【解答】(1)证明:连接BD,取DB的中点H,连接EH,FH,
∵E,H分别是AD,BD的中点,
∴EH∥AB,EHAB,
∴∠BME=∠HEF,
∵F,H分别是BC,BD的中点,
∴FH∥CD,FHCD,
∴∠CNE=∠HFE,
∵AB=CD
∴HE=FH,
∴∠HEF=∠HFE
∴∠BME=∠CNE;
(2)解:连接BD,取DB的中点H,连接EH,FH,
∵E,F分别是AD,BC的中点,
∴EHAB,FHCD,FH∥AC,
∴∠HFE=∠FEC=45°,
∵AB=CD=2,
∴HF=HE=1,
∴∠HEF=∠HFE=45°,
∴∠EHF=180°﹣∠HFE﹣HEF=90°,
∴.
15.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
【解答】解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB﹣AG=8﹣6=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EFBG=1.
故答案是:1.
16.如图所示.△ABC中,∠B,∠C的平分线BE,CF相交于O,AG⊥BE于G,AH⊥CF于H.
(1)求证:GH∥BC;
(2)若AB=9厘米,AC=14厘米,BC=18厘米,求GH.
【解答】解:(1)证明:分别延长AG,AH交BC于M,N,在△ABM中,由已知,BG平分∠ABM,BG⊥AM,所以△ABG≌△MBG(ASA).
从而,G是AM的中点.同理可证△ACH≌△NCH(ASA),
从而,H是AN的中点.所以GH是△AMN的中位线,从而,HG∥MN,即HG∥BC.
(2)解:由(1)知,△ABG≌△MBG及△ACH≌△NCH,
所以AB=BM=9厘米,AC=CN=14厘米.
又BC=18厘米,
所以BN=BC﹣CN=18﹣14=4(厘米),
MC=BC﹣BM=18﹣9=9(厘米).
从而MN=18﹣4﹣9=5(厘米),
∴GHMNcm.
17.在△ABC中,AC>BC,D为AB的中点,E为线段AC上的一点.
(1)如图1,若AEAC,∠C=90°,BC=2,AC=4,求DE的长;
(2)如图2,若AE=BC且F为EC中点,求证:∠AFD∠C;
(3)若2∠AED﹣∠C=180°,试探究AE、BC、AC的数量关系,并证明.
【解答】(1)证明:过点D作DG⊥AC交AC于G,(如图1)
∵D为AB的中点,
∴E为AC的中点,
∴DG为△ACB的中位线,
∴DGBC=1,
∵AEAC,AC=4,
∴AE=1,
在Rt△DGE中,DE;
(2)证明:连接BE,取BE中点M,再连接MF、MD.(如图2)
∵F为EC中点,D为AB中点,
∴MF∥BC且MFBC,MD∥AB且MDAE,
∴MF=MD,
∴∠MDF=∠MFD,
又∵MD∥AE,
∴∠AFD=∠MDF,
∴∠AFD∠AFM,
∵MF∥AC,
∴∠AFM=∠ACB,
∴∠AFD∠ACB,
即:∠AFD∠C;
(3)答:AC=2AE+BC,(如图3)
证明:在EC上截取EM=AE,连接BM,作CH⊥BM,
∵AE=EM,AD=DB,
∴DE∥BM,
∴∠AED=∠AMB=∠MHC+∠MCH=90°+∠MCH,
∵2∠AED﹣∠C=180°,
∴∠AED=90°∠C,
∴∠MCH∠C
∴∠C=2∠MCH,易证△CHM≌△CHB,
∴BC=MC,
∴AC=2AE+BC.
18.观察探究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 平行四边形 ;
当四边形ABCD变成矩形时,它的中点四边形是 菱形 ;
当四边形ABCD变成菱形时,它的中点四边形是 矩形 ;
当四边形ABCD变成正方形时,它的中点四边形是 正方形 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
【解答】(1)证明:连接BD.
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线.
∴EHBD,EH∥BD.
同理得FGBD,FG∥BD.
∴EH=FG,EH∥FG.
∴四边形EFGH是平行四边形.
(2)填空依次为平行四边形,菱形,矩形,正方形;
(3)中点四边形的形状是由原四边形的对角线的关系决定的.
故答案为平行四边形、菱形、矩形、正方形.
【点评】此题综合运用了三角形的中位线定理和特殊四边形的判定定理.
熟记结论:顺次连接四边形各边中点所得四边形是平行四边形;
顺次连接对角线相等的四边形各边中点所得四边形是菱形;
顺次连接对角线垂直的四边形各边中点所得四边形是矩形;
顺次连接对角线相等且互相垂直的四边形各边中点所得四边形是正方形.
19.如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.
(1)求证:CD∥AB;
(2)求证:△BDE≌△ACE;
(3)若O为AB中点,求证:OFBE.
【解答】证明:(1)∵BD=CD,
∴∠BCD=∠1;
∵∠1=∠2,
∴∠BCD=∠2;
∴CD∥AB.
(2)∵CD∥AB,∴∠CDA=∠3.
∵∠BCD=∠2=∠3,
∴BE=AE.
且∠CDA=∠BCD,
∴DE=CE.
在△BDE和△ACE中,
∵.
∴△BDE≌△ACE(SAS);
(3)∵△BDE≌△ACE,
∴∠4=∠1,∠ACE=∠BDE=90°
∴∠ACH=90°﹣∠BCH;
又∵CH⊥AB,
∴∠2=90°﹣∠BCH;
∴∠ACH=∠2=∠1=∠4,
∴AF=CF;
∵∠AEC=90°﹣∠4,∠ECF=90°﹣∠ACH,
又∵∠ACH=∠4,
∴∠AEC=∠ECF;
∴CF=EF;
∴EF=AF;
∵O为AB中点,
∴OF为△ABE的中位线;
∴OFBE.
20.如图,△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
(1)求证:DM(AC﹣AB);
(2)若AD=6,BD=8,DM=2,求AC的长.
【解答】解:
(1)证明:延长BD交AC于E,
∵AD⊥BD,
∴∠ADB=∠ADE=90°,
∵AD为∠BAC的平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中,
,
∴△BAD≌△EAD(ASA),
∴AB=AE,BD=DE,
∵M为BC的中点,
∴DMCE(AC﹣AB);
(2)∵在Rt△ADB中,∠ADB=90°,AD=6,BD=8,
∴由勾股定理得:AE=AB10,
∵DM=2,DMCE,
∴CE=4,
∴AC=10+4=14.
一.选择题(共6小题)
1.如图,△ABC的周长为20,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=8,则MN的长度为( )
A. B.2 C. D.3
2.如图,△ABC中,AB=8,AD为∠BAC的外角平分线,且AD⊥CD于点D,E为BC的中点,若DE=10,则AC的长为( )
A.12 B.14 C.16 D.18
3.如图,点D为△ABC中BC边中点,E为AD中点,BE交AC于F,若AB=4,EF=1,,则AD的长为( )
A.3 B. C.4 D.
4.如图,AC是带有滑道的铁杠,AB,CD是两段横木,E是部分嵌在滑道里的可以滑动的螺钉,BE,DE,PQ是三段橡皮筋,其中,P,Q分别是BE,DE的中点,螺钉E在滑道AC内上下滑动时,橡皮筋PQ的长度( )
A.螺钉E滑至AC两端处时,PQ的长度最大
B.螺钉E滑至AC中点处时,PQ的长度最大
C.上下滑动时,PQ的长度时而增大时而减小
D.上下滑动时,PQ的长度始终不变
5.如图,D是△ABC内部一点,AC⊥BD,且,依次取AB,BC,CD,AD的中点,并顺次连接得到四边形MNPQ,则四边形MNPQ的面积是( )
A.6 B.12 C.24 D.48
6.如图,四边形ABCD中,点E,F分别是边AB,CD的中点,且AD=6,BC=10,则线段EF的长可能为( )
A.7 B.8.5 C.9 D.10
二.填空题(共4小题)
7.如图,四边形ABCD的边DA和CB延长相交于E,H和G分别是BD和AC的中点,已知四边形ABCD的面积为33,则△EHG的面积为 .
8.如图,Rt△ABC中,∠C=90°,BC=8,D,E分别为AC,BC上的点,AD=CE=2,F,G分别为AE,BD的中点,连FG,则FG的长度是 .
9.如图,在四边形ABCD中,AD=BC,∠DAB=50°,∠CBA=70°,P、M、N分别是AB,AC、BD的中点,若BC=8,则△PMN的周长是 .
10.在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是 .
三.填空题(共10小题)
11.在△ABC中,点D是AB的中点,CE平分∠ACB,AE⊥CE于点E.
(1)求证:DE∥BC;
(2)若AC=5,BC=7,求DE的长.
12.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
13.如图,已知AO是△ABC的∠A的平分线,BD⊥AO的延长线于D,E是BC的中点.
求证:DE(AB﹣AC)
14.(1)如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.
求证:∠BME=∠CNE;(提示:取BD的中点H,连接FH,HE作辅助线)
(2)如图2,在△ABC中,F是BC边的中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=45°,求FE的长度.
15.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
16.如图所示.△ABC中,∠B,∠C的平分线BE,CF相交于O,AG⊥BE于G,AH⊥CF于H.
(1)求证:GH∥BC;
(2)若AB=9厘米,AC=14厘米,BC=18厘米,求GH.
17.在△ABC中,AC>BC,D为AB的中点,E为线段AC上的一点.
(1)如图1,若AEAC,∠C=90°,BC=2,AC=4,求DE的长;
(2)如图2,若AE=BC且F为EC中点,求证:∠AFD∠C;
(3)若2∠AED﹣∠C=180°,试探究AE、BC、AC的数量关系,并证明.
18.观察探究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 ;
当四边形ABCD变成矩形时,它的中点四边形是 ;
当四边形ABCD变成菱形时,它的中点四边形是 ;
当四边形ABCD变成正方形时,它的中点四边形是 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
19.如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.
(1)求证:CD∥AB;
(2)求证:△BDE≌△ACE;
(3)若O为AB中点,求证:OFBE.
20.如图,△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
(1)求证:DM(AC﹣AB);
(2)若AD=6,BD=8,DM=2,求AC的长.
参考答案
1.B.2.A.3.C.4.D.5.B.
6.【解答】解:连接BD,取BD的中点H,连接HF、HE,
∵点E,H分别是边AB,BD的中点,
∴EH是△ABD的中位线,
∴EHAD=3,
同理可得:FHBC=5,
∴FH﹣EH≤EF≤FH+EH,即2≤EF≤8,
故选:A.
7.【解答】解:连接AH,CH,BG,如图:
设S△AHG=S△HGC=m,S△ABG=S△BGC=n,
∵S△ADH=S△AHB,S△DHC=S△BHC,
∴S△ADH+S△DHC=S△AHB+S△BHC=2m+2n,
∴S四边形ABCD=2(S△ADH+S△DHC)=4m+4n,
∴,
设S△ABE=x,则,
∴.
故答案为:.
8.【解答】解:如图,取AB的中点H,连接HF,HG并延长交AC于点I,交BC于点J,
∵F,G分别为AE,BD的中点,
∴HG是△ABD的中位线,HF是△AEB的中位线,
∴HG,HG∥AC,HF,HF∥BC,
∴四边形IHJC是平行四边形,
∵∠C=90°,
∴四边形IHJC是矩形,
∴∠FHG=90°,
∴FG,
故答案为:.
9.【解答】解:∵P、N是AB和BD的中点,
∴PNAD8=4,PN∥AD,
∴∠NPB=∠DAB=50°,
同理,PM=4,∠MPA=∠CBA=70°,
∴PM=PN=4,∠MPN=180°﹣50°﹣70°=60°,
∴△PMN是等边三角形.
∴MN=PM=PN=4,
∴△PMN的周长是12.
10.【解答】解:连接CM,
∵点D、E分别为CN,MN的中点,
∴DECM,
当CM⊥AB时,CM的值最小,此时DE的值也最小,
由勾股定理得:AB5,
∵S△ABC,
∴CM,
∴DE,
故答案为:.
11.在△ABC中,点D是AB的中点,CE平分∠ACB,AE⊥CE于点E.
(1)求证:DE∥BC;
(2)若AC=5,BC=7,求DE的长.
【解答】解:(1)延长AE交BC于F,
∵CE平分∠ACB,AE⊥CE于点E,
∴∠ACE=∠FCE,∠AEC=∠FEC=90°,
在△ACE和△FCE中,
,
∴△ACE≌△FCE.
∴AE=EF,
∵点D是AB的中点,
∴AD=BD,
∴DE是△ABF的中位线.
∴DE∥BC;
(2)∵△ACE≌△FCE,
∴CF=AC=5,
∵DE是△ABF的中位线.
∴DEBF(BC﹣AC)(7﹣5)=1,
故DE的长为1.
12.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
【解答】(1)解:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,AB=6,CD=8,
∴PE是△ADB的中位线,
∴PE∥AB,且PEAB=3,PF∥CD且PFCD=4.
又∵∠ABD=30°,∠BDC=120°,
∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在直角△EPF中,由勾股定理得到:EF5,
即EF=5;
(2)证明:如图,取BD的中点P,连接EP、FP.
∵E,F分别是AD、BC的中点,
∴PE∥AB,且PEAB,PF∥CD且PFCD.
∴∠EPD=∠ABD,∠BPF=∠BDC,
∴∠DPF=180°﹣∠BPF=180°﹣∠BDC,
∵∠BDC﹣∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,
∴PE2+PF2=(AB)2+(CD)2=EF2,
∴AB2+CD2=4EF2.
13.如图,已知AO是△ABC的∠A的平分线,BD⊥AO的延长线于D,E是BC的中点.
求证:DE(AB﹣AC)
【解答】证明:延长AC、BD交于点F,
∵在△ABD和△AFD中,
,
∴△ABD≌△AFD(ASA),
∴AB=AF,BD=DF,
又∵E是BC的中点,即ED是△BCF中位线,
∴DECF(AB﹣AC).
14.(1)如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.
求证:∠BME=∠CNE;(提示:取BD的中点H,连接FH,HE作辅助线)
(2)如图2,在△ABC中,F是BC边的中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=45°,求FE的长度.
【解答】(1)证明:连接BD,取DB的中点H,连接EH,FH,
∵E,H分别是AD,BD的中点,
∴EH∥AB,EHAB,
∴∠BME=∠HEF,
∵F,H分别是BC,BD的中点,
∴FH∥CD,FHCD,
∴∠CNE=∠HFE,
∵AB=CD
∴HE=FH,
∴∠HEF=∠HFE
∴∠BME=∠CNE;
(2)解:连接BD,取DB的中点H,连接EH,FH,
∵E,F分别是AD,BC的中点,
∴EHAB,FHCD,FH∥AC,
∴∠HFE=∠FEC=45°,
∵AB=CD=2,
∴HF=HE=1,
∴∠HEF=∠HFE=45°,
∴∠EHF=180°﹣∠HFE﹣HEF=90°,
∴.
15.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
【解答】解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB﹣AG=8﹣6=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EFBG=1.
故答案是:1.
16.如图所示.△ABC中,∠B,∠C的平分线BE,CF相交于O,AG⊥BE于G,AH⊥CF于H.
(1)求证:GH∥BC;
(2)若AB=9厘米,AC=14厘米,BC=18厘米,求GH.
【解答】解:(1)证明:分别延长AG,AH交BC于M,N,在△ABM中,由已知,BG平分∠ABM,BG⊥AM,所以△ABG≌△MBG(ASA).
从而,G是AM的中点.同理可证△ACH≌△NCH(ASA),
从而,H是AN的中点.所以GH是△AMN的中位线,从而,HG∥MN,即HG∥BC.
(2)解:由(1)知,△ABG≌△MBG及△ACH≌△NCH,
所以AB=BM=9厘米,AC=CN=14厘米.
又BC=18厘米,
所以BN=BC﹣CN=18﹣14=4(厘米),
MC=BC﹣BM=18﹣9=9(厘米).
从而MN=18﹣4﹣9=5(厘米),
∴GHMNcm.
17.在△ABC中,AC>BC,D为AB的中点,E为线段AC上的一点.
(1)如图1,若AEAC,∠C=90°,BC=2,AC=4,求DE的长;
(2)如图2,若AE=BC且F为EC中点,求证:∠AFD∠C;
(3)若2∠AED﹣∠C=180°,试探究AE、BC、AC的数量关系,并证明.
【解答】(1)证明:过点D作DG⊥AC交AC于G,(如图1)
∵D为AB的中点,
∴E为AC的中点,
∴DG为△ACB的中位线,
∴DGBC=1,
∵AEAC,AC=4,
∴AE=1,
在Rt△DGE中,DE;
(2)证明:连接BE,取BE中点M,再连接MF、MD.(如图2)
∵F为EC中点,D为AB中点,
∴MF∥BC且MFBC,MD∥AB且MDAE,
∴MF=MD,
∴∠MDF=∠MFD,
又∵MD∥AE,
∴∠AFD=∠MDF,
∴∠AFD∠AFM,
∵MF∥AC,
∴∠AFM=∠ACB,
∴∠AFD∠ACB,
即:∠AFD∠C;
(3)答:AC=2AE+BC,(如图3)
证明:在EC上截取EM=AE,连接BM,作CH⊥BM,
∵AE=EM,AD=DB,
∴DE∥BM,
∴∠AED=∠AMB=∠MHC+∠MCH=90°+∠MCH,
∵2∠AED﹣∠C=180°,
∴∠AED=90°∠C,
∴∠MCH∠C
∴∠C=2∠MCH,易证△CHM≌△CHB,
∴BC=MC,
∴AC=2AE+BC.
18.观察探究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 平行四边形 ;
当四边形ABCD变成矩形时,它的中点四边形是 菱形 ;
当四边形ABCD变成菱形时,它的中点四边形是 矩形 ;
当四边形ABCD变成正方形时,它的中点四边形是 正方形 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
【解答】(1)证明:连接BD.
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线.
∴EHBD,EH∥BD.
同理得FGBD,FG∥BD.
∴EH=FG,EH∥FG.
∴四边形EFGH是平行四边形.
(2)填空依次为平行四边形,菱形,矩形,正方形;
(3)中点四边形的形状是由原四边形的对角线的关系决定的.
故答案为平行四边形、菱形、矩形、正方形.
【点评】此题综合运用了三角形的中位线定理和特殊四边形的判定定理.
熟记结论:顺次连接四边形各边中点所得四边形是平行四边形;
顺次连接对角线相等的四边形各边中点所得四边形是菱形;
顺次连接对角线垂直的四边形各边中点所得四边形是矩形;
顺次连接对角线相等且互相垂直的四边形各边中点所得四边形是正方形.
19.如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.
(1)求证:CD∥AB;
(2)求证:△BDE≌△ACE;
(3)若O为AB中点,求证:OFBE.
【解答】证明:(1)∵BD=CD,
∴∠BCD=∠1;
∵∠1=∠2,
∴∠BCD=∠2;
∴CD∥AB.
(2)∵CD∥AB,∴∠CDA=∠3.
∵∠BCD=∠2=∠3,
∴BE=AE.
且∠CDA=∠BCD,
∴DE=CE.
在△BDE和△ACE中,
∵.
∴△BDE≌△ACE(SAS);
(3)∵△BDE≌△ACE,
∴∠4=∠1,∠ACE=∠BDE=90°
∴∠ACH=90°﹣∠BCH;
又∵CH⊥AB,
∴∠2=90°﹣∠BCH;
∴∠ACH=∠2=∠1=∠4,
∴AF=CF;
∵∠AEC=90°﹣∠4,∠ECF=90°﹣∠ACH,
又∵∠ACH=∠4,
∴∠AEC=∠ECF;
∴CF=EF;
∴EF=AF;
∵O为AB中点,
∴OF为△ABE的中位线;
∴OFBE.
20.如图,△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
(1)求证:DM(AC﹣AB);
(2)若AD=6,BD=8,DM=2,求AC的长.
【解答】解:
(1)证明:延长BD交AC于E,
∵AD⊥BD,
∴∠ADB=∠ADE=90°,
∵AD为∠BAC的平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中,
,
∴△BAD≌△EAD(ASA),
∴AB=AE,BD=DE,
∵M为BC的中点,
∴DMCE(AC﹣AB);
(2)∵在Rt△ADB中,∠ADB=90°,AD=6,BD=8,
∴由勾股定理得:AE=AB10,
∵DM=2,DMCE,
∴CE=4,
∴AC=10+4=14.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
