6.4多边形内角和和外角和培优练习(含答案)
文档属性
| 名称 | 6.4多边形内角和和外角和培优练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 858.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 17:02:21 | ||
图片预览



文档简介
6.4多边形内角和和外角和培优练习北师大版2024—2025学年八年级下册
一.选择题
1.从n边形的一个顶点出发作对角线,可以把这个n边形分成9个三角形,则n等于( )
A.9 B.10 C.11 D.12
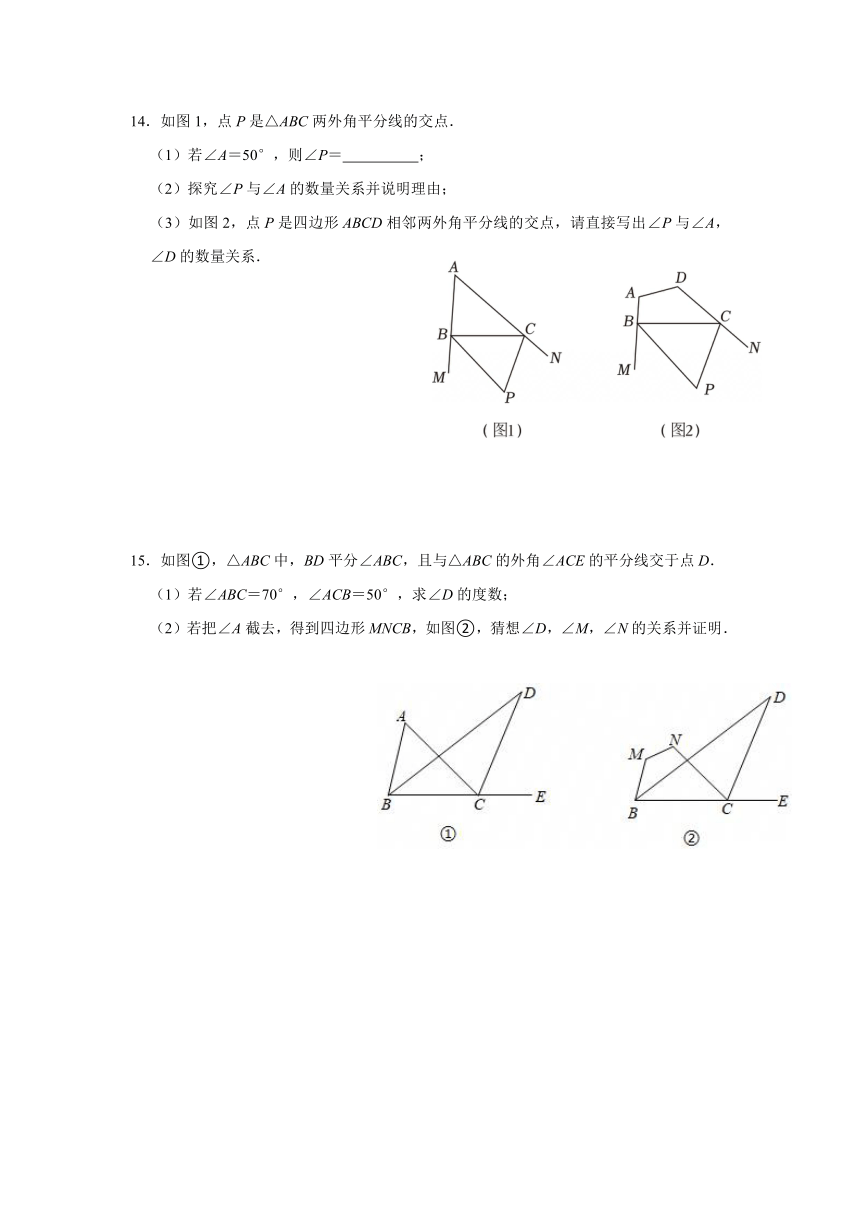
2.如图,已知∠1+∠2+∠3+∠4=280°,那么∠5的度数为( )
A.70° B.80° C.90° D.100°
3.如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.360° B.480° C.540° D.720°
二.填空题
4.一个多边形的内角和比它的外角和多540°,并且这个多边形的各个内角都相等,则这个多边形每个内角是 .
5.如图,正五边形ABCDE和正六边形EFGHMN的边CD、FG在直线l上,正五边形在正六边形左侧,两个正多边形均在l的同侧,则∠DEF的大小是 度.
6.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了 m.
7.如图,△ABE在四边形ABCD内部,若∠C=78°,∠D=66°,∠E=40°,则∠1+∠2= .
三.解答题
8.已知一个多边形的边数为n.
(1)若n=8,求这个多边形的内角和.
(2)若这个多边形的每个内角都比与它相邻外角的3倍还多20°求n的值.
9.如图,∠A+∠B+∠D+∠E=280°,求∠C的度数.
10.如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.
(1)五边形ABCDE的内角和为 度;
(2)若∠C=100°,∠D=75°,∠E=135°,求∠P的度数.
11.如图,在四边形ABCD中,AD∥BC,BD⊥CD,点E,F分别在BC,CD上,EF⊥CD.
(1)求证:∠1=∠2;
(2)若∠A=100°,BD平分∠ABC,求∠ADC的度数.
12.如图,已知:在四边形ABCD中,AB∥CD,AD∥BC,点E为线段CB延长线上一点,连接DE交AB于点F,∠CBD=∠CDE.
(1)求证:∠ADE=∠BDC;
(2)若BA是∠DBE的角平分线,∠CBD=76°,求∠ADE的度数.
13.解决下列问题.
(1)如图1,计算下列五角星图案中五个顶角的度数和.即:求∠A+∠B+∠C+∠D+∠E的大小.
(2)如图2,若五角星的五个顶角的度数相等,求∠1的大小.
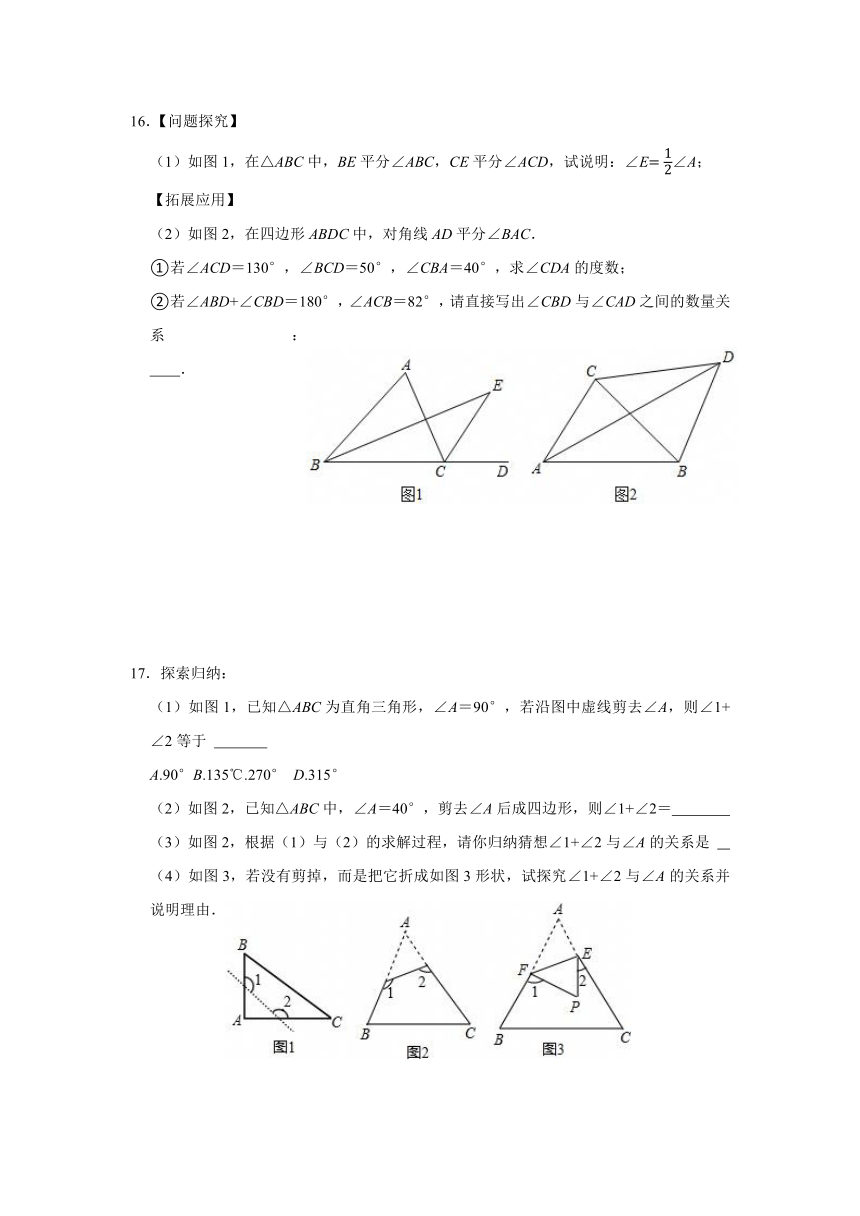
14.如图1,点P是△ABC两外角平分线的交点.
(1)若∠A=50°,则∠P= ;
(2)探究∠P与∠A的数量关系并说明理由;
(3)如图2,点P是四边形ABCD相邻两外角平分线的交点,请直接写出∠P与∠A,∠D的数量关系.
15.如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的平分线交于点D.
(1)若∠ABC=70°,∠ACB=50°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D,∠M,∠N的关系并证明.
16.【问题探究】
(1)如图1,在△ABC中,BE平分∠ABC,CE平分∠ACD,试说明:∠E∠A;
【拓展应用】
(2)如图2,在四边形ABDC中,对角线AD平分∠BAC.
①若∠ACD=130°,∠BCD=50°,∠CBA=40°,求∠CDA的度数;
②若∠ABD+∠CBD=180°,∠ACB=82°,请直接写出∠CBD与∠CAD之间的数量关系: .
17.探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于
A.90°B.135℃.270° D.315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
18.如图,求∠A+∠B+∠C+∠D+∠E的度数.
19.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=460°.
(1)求六边形ABCDEF的内角和;
(2)求∠BGD的度数.
20.已知:从n边形的一个顶点出发共有4条对角线;从m边形的一个顶点出发的所有对角线把m边形分成6个三角形;正t边形内角和等于外角和的4倍,求(n﹣m)t的值.
21“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
22.如图所示:
求∠A+∠D+∠B+∠E+∠C+∠F的度数.
23.四边形ABCD中,AD∥BC,AC交BD于点O.点E、F分别在OA、OB上,作射线DE、CF交AB分别于点M、N.n.
(1)当n=1,AC⊥BD时,①求∠ADO+∠BCO的值;②求∠DEO+∠CFO的值.
(2)当n=2,试探究:∠AMD+∠BNC与∠DOC的数量关系,证明你的结论.
参考答案
1.【解答】解:依题意有n﹣2=9,
解得:n=11.
故选:C.
2.【解答】解:由题意得:
∠1+2+∠3+∠4+∠5=360°,
∵∠1+2+∠3+∠4=280°,
∴∠5=360°﹣280°=80°,
故选:B.
3.【解答】解:如图,AC、DF与BE分别相交于点M、N,
在四边形NMCD中,∠MND+∠CMN+∠C+∠D=360°,
∵∠CMN=∠A+∠E,∠MND=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故选:A.
4.【解答】解:设这个多边形的边数为n,
则有(n﹣2) 180°=360°+540°,
解得n=7.
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为900°÷7=()°.
故答案为:()°.
5.【解答】解:∵五边形ABCDE是正五边形,
∴每个内角度数为108°.
∴∠EDC=108°,
∴∠EDF=72°,
同理可得正六边形BFGHMN每个内角度数为120°.
∴∠EFG=120°,
∴∠EFD=60°,
∴∠DEF=180°﹣∠EDF﹣∠EFD=180°﹣72°﹣60°=48°.
解法二:∵五边形ABCDE是正五边形,
∴∠EDF=72°,
∵六边形EFGHMN是正六边形,
∴∠EFD=60°,
∴∠DEF=180°﹣∠EDF﹣∠EFD=180°﹣72°﹣60°=48°;
故答案为:48.
6.【解答】解:∵小亮从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为n=360°÷15°=24,
则一共走了24×10=240(米).
故答案为:240.
【点评】本题主要考查了多边形的外角和定理,掌握任何一个多边形的外角和都是360°是解题的关键.
7.【解答】解:在△ABE中,∠E=40°,
∴∠EAB+∠EBA=180°﹣∠E=140°,
∴∠DAB+∠CBA=∠1+∠2+(∠EAB+∠EBA)=∠1+∠2+140°
在四边形ABCD中,∠DAB+∠CBA+∠C+∠D=360°,
∵∠C=78°,∠D=66°,
∴∠1+∠2+140°+78°+66°=360°,
∴∠1+∠2=76°,
故答案为:76°.
三.解答题
8.【解答】解:(1)多边形的内角和=(8﹣2)×180°=1080°,
答:这个多边形的内角和1080°;
(2)设这个多边形的每个外角为x°,则每个内角为(3x+20)°,
依题意得,3x+20+x=180,
解得x=40,
∴n=360°÷40°=9,
答:这个多边形的边数n为9.
9.【解答】解:连接BD,
∵四边形的内角和为360°,
∴∠A+∠ABD+∠BDE+∠E=360°,
∵∠A+∠ABC+∠CDE+∠E=280°,
∴∠CBD+∠BDC=360°﹣280°=80°,
∴∠C=180°﹣(∠CBD+∠BDC)=180°﹣80°=100°.
10.【解答】解:(1)五边形ABCDE的内角和为(5﹣2)×180°=540°,
故答案为:540;
(2)∵在五边形ABCDE中,∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=230°,
∵AP平分∠EAB,BP平分∠ABC,
∴∠PAB∠EAB,∠PBA∠ABC,
∴∠PAB+∠PBA=115°,
∴∠P=180°﹣(∠PAB+∠PBA)=65°.
11.【解答】(1)证明:∵AD∥BC,
∴∠1=∠3,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠2=∠3,
∴∠1=∠2;
(2)解:∵AD∥BC,
∴∠A+∠ABC=180°,∠1=∠DBC,
∴∠ABC=80°,
∵BD平分∠ABC,
∴,
∴∠1=40°,
∵BD⊥CD,
∴∠BDC=90°,
∴∠ADC=∠1+∠BDC=130°.
12.【解答】(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵∠CBD=∠CDE,
∴∠CDE=∠ADB,
∵∠ADE+∠EDB=∠ADB,
∠BDC+∠EDB=∠CDE,
∴∠ADE=∠BDC;
(2)解:∵BA是∠DBE的角平分线,
∴∠ABE=∠ABD∠DBE,
∵∠DBE+∠CBD=180°,∠CBD=76°,
∴∠DBE=104°,
∴∠ABE=∠ABD=52°,
∵AB∥CD,
∴∠C=∠ABE=52°,
∵AD∥BC,
∴∠CBD=∠ADB=76°,∠C+∠ADC=180°,
∴∠ADC=180°﹣52°=128°,
∴∠BDC=∠ADC﹣∠ADB=128°﹣76°=52°,
∵∠ADE=∠BDC,
∴∠ADE=52°.
13.【解答】解:(1)∵∠AFG是△FEC的外角,
∴∠AFG=∠C+∠E,
同理可得:
∠AGF=∠B+∠D,
在△AFG中,
∴∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
(2)∵五角星的五个顶角的度数相等,
∴,
∴∠AGB=∠B+∠D=2×36°=72°,
∵∠1+∠AGB=180°,
∴∠1=180°﹣∠AGB=180°﹣72°=108°.
14.【解答】解:(1)∵点P是△ABC两外角平分线的交点,
∴∠PBC+∠PCB(∠MBC+∠NCB)(180°﹣∠ABC+180°﹣∠ACB)[360°﹣(180°﹣∠A)](180+∠A),
在△PBC中,∠P=180°(180°+∠A)=90°∠A,
∵∠A=50°,
∴∠P=65°;
故答案为:65°;
(2)∵BP,CP分别是外角∠DBC,∠ECB的平分线,
∴∠PBC+∠PCB(∠DBC+∠ECB)(180°+∠A),
在△PBC中,∠P=180°(180°﹣∠A)=90°∠A.
(3)如图,
延长BA、CD交于Q,
则∠P=90°∠Q,
∴∠Q=180°﹣2∠P.
∴∠BAD+∠CDA
=180°+∠Q
=180°+180°﹣2∠P
=360°﹣2∠P.
15.【解答】(1)解:如图①,
∵BD平分∠ABC,CD平分∠ACE,
∴∠ABO∠ABC,∠ACD∠ACE,
∵∠AOB=∠DOC,
∴∠A+∠ABO=∠D+∠DCO,
∴∠A∠ABC=∠D∠ACE,
∴∠A∠ABC=∠D(∠A+∠ABC),
∴∠A∠ABC=∠D∠A∠ABC,
∴∠D∠A,
∵∠A=180°﹣∠ABC﹣∠ACB=60°,
∴∠D60°=30°;
(2)如图②,
∠D与∠BMN,∠CNM的关系为:∠D(∠BMN+∠CNM﹣180°),
证明:延长BM,CN交于点A,
∵∠BMN=∠A+∠ANM,∠CNM=∠A+∠AMN,
∴(∠BMN+∠CNM)=∠A+∠ANM+∠A+∠AMN=∠A+180°,
∴∠A=∠BMN+∠CNM﹣180°,
由(1)∠D∠A,
∴∠D(∠BMN+∠CNM﹣180°).
16.【解答】(1)证明:∵CE平分∠ACD,
∴∠ECD∠ACD,
∵∠ACD=∠A+∠ABC,
∴∠ECD(∠A+∠ABC).
又∵∠ECD=∠E+∠EBC,
∴∠E+∠EBC(∠A+∠ABC).
∵BE平分∠ABC,
∴∠EBC∠ABC,
∴∠ABC+∠E(∠A+∠ABC),
∴∠E∠A;
(2)解:①∵∠ACD=130°,∠BCD=50°,
∴∠ACB=∠ACD﹣∠BCD=130°﹣50°=80°,
∵∠CBA=40°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=180°﹣80°﹣40°=60°,
∵AD平分∠BAC,
∴∠CADCAB=30°,
∴∠ADC=180°﹣∠CAD﹣∠ACD=20°;
②设∠CBD=α,
∵∠ABD+∠CBD=180°,
∴∠ABC=180°﹣2α,
∵∠ACB=82°,
∴∠CAB=180°﹣∠ABC﹣∠ACB=180°﹣(180°﹣2α)﹣82°=2α﹣82°,
∵AD平分∠BAC,
∴∠CADCAB=α﹣41°,
∴∠CAD+41°=∠CBD,
故答案为:∠CAD+41°=∠CBD.
17.【解答】解:(1):∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2等于270°.
故选C;
(2)∠1+∠2=180°+40°=220°,
故答案为:220°;
(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;
(4)∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF
∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF
∴∠1+∠2=360°﹣2(∠AFE+∠AEF)
又∵∠AFE+∠AEF=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.
18.【解答】解:连接BC,
∵∠D+∠E+∠1=∠3+∠4+∠2=180°,
又∵∠1=∠2,
∴∠D+∠E=∠3+∠4,
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠ABE+∠ACD+∠3+∠4
=∠A+∠ABC+∠ACB
=180°.
19.【解答】解:(1)六边形ABCDEF的内角和为:180°×(6﹣2)=720°;
(2)∵六边形ABCDEF的内角和为720°,∠1+∠2+∠3+∠4+∠5=460°,
∴∠GBC+∠C+∠CDG=720°﹣460°=260°,
∴∠BGD=360°﹣(∠GBC+∠C+∠CDG)=100°.
即∠BGD的度数是100°.
20.【解答】解:依题意有n=4+3=7,
m=6+2=8,
(t﹣2)×180°=360°×4,
解得t=10,
则(n﹣m)t=(7﹣8)10=1.
21.【解答】解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
22.【解答】解:由图可得,
∠A+∠D+∠B+∠E+∠C+∠F的和正好是中间小三角形的三个外角之和,
∵三角形的外角和是360°,
∴∠A+∠D+∠B+∠E+∠C+∠F=360°.
23.【解答】解:(1)∵AD∥BC,
∴∠ADO=∠OBC.
∵1,
∴可设∠ODE=∠ADE=α,∠OCF=∠BCF=β.
∵AC⊥BD,
∴∠DOC=90°,
∴∠OBC+∠BCO=90°,
∴∠ADO+∠BCO=90°;
∴2α+2β=90°,
∴α+β=45°.
∵∠DEO=90°﹣α,∠CFO=90°﹣β,
∴∠DEO+∠CFO=90°﹣α+90°﹣β=180°﹣(α+β)=135°;
(2)∠AMD+∠BNC=180°∠DOC.理由如下:
∵AD∥BC,
∴∠ADO=∠OBC,∠DAB+∠ABC=180°.
∵2,
∴可设∠ADE=γ,∠BCF=θ,则∠ODE=2γ,∠OCF=2θ.
∵∠AMD+∠BNC=180°﹣∠DAB﹣γ+180°﹣∠ABC﹣θ=360°﹣(∠DAB+∠ABC)﹣(γ+θ)=180°﹣(γ+θ),
∠DOC=∠OBC+∠BCO=∠ADO+∠BCO=3γ+3θ=3(γ+θ),
∴∠AMD+∠BNC=180°∠DOC.
一.选择题
1.从n边形的一个顶点出发作对角线,可以把这个n边形分成9个三角形,则n等于( )
A.9 B.10 C.11 D.12
2.如图,已知∠1+∠2+∠3+∠4=280°,那么∠5的度数为( )
A.70° B.80° C.90° D.100°
3.如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.360° B.480° C.540° D.720°
二.填空题
4.一个多边形的内角和比它的外角和多540°,并且这个多边形的各个内角都相等,则这个多边形每个内角是 .
5.如图,正五边形ABCDE和正六边形EFGHMN的边CD、FG在直线l上,正五边形在正六边形左侧,两个正多边形均在l的同侧,则∠DEF的大小是 度.
6.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了 m.
7.如图,△ABE在四边形ABCD内部,若∠C=78°,∠D=66°,∠E=40°,则∠1+∠2= .
三.解答题
8.已知一个多边形的边数为n.
(1)若n=8,求这个多边形的内角和.
(2)若这个多边形的每个内角都比与它相邻外角的3倍还多20°求n的值.
9.如图,∠A+∠B+∠D+∠E=280°,求∠C的度数.
10.如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.
(1)五边形ABCDE的内角和为 度;
(2)若∠C=100°,∠D=75°,∠E=135°,求∠P的度数.
11.如图,在四边形ABCD中,AD∥BC,BD⊥CD,点E,F分别在BC,CD上,EF⊥CD.
(1)求证:∠1=∠2;
(2)若∠A=100°,BD平分∠ABC,求∠ADC的度数.
12.如图,已知:在四边形ABCD中,AB∥CD,AD∥BC,点E为线段CB延长线上一点,连接DE交AB于点F,∠CBD=∠CDE.
(1)求证:∠ADE=∠BDC;
(2)若BA是∠DBE的角平分线,∠CBD=76°,求∠ADE的度数.
13.解决下列问题.
(1)如图1,计算下列五角星图案中五个顶角的度数和.即:求∠A+∠B+∠C+∠D+∠E的大小.
(2)如图2,若五角星的五个顶角的度数相等,求∠1的大小.
14.如图1,点P是△ABC两外角平分线的交点.
(1)若∠A=50°,则∠P= ;
(2)探究∠P与∠A的数量关系并说明理由;
(3)如图2,点P是四边形ABCD相邻两外角平分线的交点,请直接写出∠P与∠A,∠D的数量关系.
15.如图①,△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的平分线交于点D.
(1)若∠ABC=70°,∠ACB=50°,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D,∠M,∠N的关系并证明.
16.【问题探究】
(1)如图1,在△ABC中,BE平分∠ABC,CE平分∠ACD,试说明:∠E∠A;
【拓展应用】
(2)如图2,在四边形ABDC中,对角线AD平分∠BAC.
①若∠ACD=130°,∠BCD=50°,∠CBA=40°,求∠CDA的度数;
②若∠ABD+∠CBD=180°,∠ACB=82°,请直接写出∠CBD与∠CAD之间的数量关系: .
17.探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于
A.90°B.135℃.270° D.315°
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
18.如图,求∠A+∠B+∠C+∠D+∠E的度数.
19.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=460°.
(1)求六边形ABCDEF的内角和;
(2)求∠BGD的度数.
20.已知:从n边形的一个顶点出发共有4条对角线;从m边形的一个顶点出发的所有对角线把m边形分成6个三角形;正t边形内角和等于外角和的4倍,求(n﹣m)t的值.
21“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
22.如图所示:
求∠A+∠D+∠B+∠E+∠C+∠F的度数.
23.四边形ABCD中,AD∥BC,AC交BD于点O.点E、F分别在OA、OB上,作射线DE、CF交AB分别于点M、N.n.
(1)当n=1,AC⊥BD时,①求∠ADO+∠BCO的值;②求∠DEO+∠CFO的值.
(2)当n=2,试探究:∠AMD+∠BNC与∠DOC的数量关系,证明你的结论.
参考答案
1.【解答】解:依题意有n﹣2=9,
解得:n=11.
故选:C.
2.【解答】解:由题意得:
∠1+2+∠3+∠4+∠5=360°,
∵∠1+2+∠3+∠4=280°,
∴∠5=360°﹣280°=80°,
故选:B.
3.【解答】解:如图,AC、DF与BE分别相交于点M、N,
在四边形NMCD中,∠MND+∠CMN+∠C+∠D=360°,
∵∠CMN=∠A+∠E,∠MND=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故选:A.
4.【解答】解:设这个多边形的边数为n,
则有(n﹣2) 180°=360°+540°,
解得n=7.
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为900°÷7=()°.
故答案为:()°.
5.【解答】解:∵五边形ABCDE是正五边形,
∴每个内角度数为108°.
∴∠EDC=108°,
∴∠EDF=72°,
同理可得正六边形BFGHMN每个内角度数为120°.
∴∠EFG=120°,
∴∠EFD=60°,
∴∠DEF=180°﹣∠EDF﹣∠EFD=180°﹣72°﹣60°=48°.
解法二:∵五边形ABCDE是正五边形,
∴∠EDF=72°,
∵六边形EFGHMN是正六边形,
∴∠EFD=60°,
∴∠DEF=180°﹣∠EDF﹣∠EFD=180°﹣72°﹣60°=48°;
故答案为:48.
6.【解答】解:∵小亮从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为n=360°÷15°=24,
则一共走了24×10=240(米).
故答案为:240.
【点评】本题主要考查了多边形的外角和定理,掌握任何一个多边形的外角和都是360°是解题的关键.
7.【解答】解:在△ABE中,∠E=40°,
∴∠EAB+∠EBA=180°﹣∠E=140°,
∴∠DAB+∠CBA=∠1+∠2+(∠EAB+∠EBA)=∠1+∠2+140°
在四边形ABCD中,∠DAB+∠CBA+∠C+∠D=360°,
∵∠C=78°,∠D=66°,
∴∠1+∠2+140°+78°+66°=360°,
∴∠1+∠2=76°,
故答案为:76°.
三.解答题
8.【解答】解:(1)多边形的内角和=(8﹣2)×180°=1080°,
答:这个多边形的内角和1080°;
(2)设这个多边形的每个外角为x°,则每个内角为(3x+20)°,
依题意得,3x+20+x=180,
解得x=40,
∴n=360°÷40°=9,
答:这个多边形的边数n为9.
9.【解答】解:连接BD,
∵四边形的内角和为360°,
∴∠A+∠ABD+∠BDE+∠E=360°,
∵∠A+∠ABC+∠CDE+∠E=280°,
∴∠CBD+∠BDC=360°﹣280°=80°,
∴∠C=180°﹣(∠CBD+∠BDC)=180°﹣80°=100°.
10.【解答】解:(1)五边形ABCDE的内角和为(5﹣2)×180°=540°,
故答案为:540;
(2)∵在五边形ABCDE中,∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,
∴∠EAB+∠ABC=230°,
∵AP平分∠EAB,BP平分∠ABC,
∴∠PAB∠EAB,∠PBA∠ABC,
∴∠PAB+∠PBA=115°,
∴∠P=180°﹣(∠PAB+∠PBA)=65°.
11.【解答】(1)证明:∵AD∥BC,
∴∠1=∠3,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠2=∠3,
∴∠1=∠2;
(2)解:∵AD∥BC,
∴∠A+∠ABC=180°,∠1=∠DBC,
∴∠ABC=80°,
∵BD平分∠ABC,
∴,
∴∠1=40°,
∵BD⊥CD,
∴∠BDC=90°,
∴∠ADC=∠1+∠BDC=130°.
12.【解答】(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵∠CBD=∠CDE,
∴∠CDE=∠ADB,
∵∠ADE+∠EDB=∠ADB,
∠BDC+∠EDB=∠CDE,
∴∠ADE=∠BDC;
(2)解:∵BA是∠DBE的角平分线,
∴∠ABE=∠ABD∠DBE,
∵∠DBE+∠CBD=180°,∠CBD=76°,
∴∠DBE=104°,
∴∠ABE=∠ABD=52°,
∵AB∥CD,
∴∠C=∠ABE=52°,
∵AD∥BC,
∴∠CBD=∠ADB=76°,∠C+∠ADC=180°,
∴∠ADC=180°﹣52°=128°,
∴∠BDC=∠ADC﹣∠ADB=128°﹣76°=52°,
∵∠ADE=∠BDC,
∴∠ADE=52°.
13.【解答】解:(1)∵∠AFG是△FEC的外角,
∴∠AFG=∠C+∠E,
同理可得:
∠AGF=∠B+∠D,
在△AFG中,
∴∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
(2)∵五角星的五个顶角的度数相等,
∴,
∴∠AGB=∠B+∠D=2×36°=72°,
∵∠1+∠AGB=180°,
∴∠1=180°﹣∠AGB=180°﹣72°=108°.
14.【解答】解:(1)∵点P是△ABC两外角平分线的交点,
∴∠PBC+∠PCB(∠MBC+∠NCB)(180°﹣∠ABC+180°﹣∠ACB)[360°﹣(180°﹣∠A)](180+∠A),
在△PBC中,∠P=180°(180°+∠A)=90°∠A,
∵∠A=50°,
∴∠P=65°;
故答案为:65°;
(2)∵BP,CP分别是外角∠DBC,∠ECB的平分线,
∴∠PBC+∠PCB(∠DBC+∠ECB)(180°+∠A),
在△PBC中,∠P=180°(180°﹣∠A)=90°∠A.
(3)如图,
延长BA、CD交于Q,
则∠P=90°∠Q,
∴∠Q=180°﹣2∠P.
∴∠BAD+∠CDA
=180°+∠Q
=180°+180°﹣2∠P
=360°﹣2∠P.
15.【解答】(1)解:如图①,
∵BD平分∠ABC,CD平分∠ACE,
∴∠ABO∠ABC,∠ACD∠ACE,
∵∠AOB=∠DOC,
∴∠A+∠ABO=∠D+∠DCO,
∴∠A∠ABC=∠D∠ACE,
∴∠A∠ABC=∠D(∠A+∠ABC),
∴∠A∠ABC=∠D∠A∠ABC,
∴∠D∠A,
∵∠A=180°﹣∠ABC﹣∠ACB=60°,
∴∠D60°=30°;
(2)如图②,
∠D与∠BMN,∠CNM的关系为:∠D(∠BMN+∠CNM﹣180°),
证明:延长BM,CN交于点A,
∵∠BMN=∠A+∠ANM,∠CNM=∠A+∠AMN,
∴(∠BMN+∠CNM)=∠A+∠ANM+∠A+∠AMN=∠A+180°,
∴∠A=∠BMN+∠CNM﹣180°,
由(1)∠D∠A,
∴∠D(∠BMN+∠CNM﹣180°).
16.【解答】(1)证明:∵CE平分∠ACD,
∴∠ECD∠ACD,
∵∠ACD=∠A+∠ABC,
∴∠ECD(∠A+∠ABC).
又∵∠ECD=∠E+∠EBC,
∴∠E+∠EBC(∠A+∠ABC).
∵BE平分∠ABC,
∴∠EBC∠ABC,
∴∠ABC+∠E(∠A+∠ABC),
∴∠E∠A;
(2)解:①∵∠ACD=130°,∠BCD=50°,
∴∠ACB=∠ACD﹣∠BCD=130°﹣50°=80°,
∵∠CBA=40°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=180°﹣80°﹣40°=60°,
∵AD平分∠BAC,
∴∠CADCAB=30°,
∴∠ADC=180°﹣∠CAD﹣∠ACD=20°;
②设∠CBD=α,
∵∠ABD+∠CBD=180°,
∴∠ABC=180°﹣2α,
∵∠ACB=82°,
∴∠CAB=180°﹣∠ABC﹣∠ACB=180°﹣(180°﹣2α)﹣82°=2α﹣82°,
∵AD平分∠BAC,
∴∠CADCAB=α﹣41°,
∴∠CAD+41°=∠CBD,
故答案为:∠CAD+41°=∠CBD.
17.【解答】解:(1):∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2等于270°.
故选C;
(2)∠1+∠2=180°+40°=220°,
故答案为:220°;
(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;
(4)∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF
∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF
∴∠1+∠2=360°﹣2(∠AFE+∠AEF)
又∵∠AFE+∠AEF=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.
18.【解答】解:连接BC,
∵∠D+∠E+∠1=∠3+∠4+∠2=180°,
又∵∠1=∠2,
∴∠D+∠E=∠3+∠4,
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠ABE+∠ACD+∠3+∠4
=∠A+∠ABC+∠ACB
=180°.
19.【解答】解:(1)六边形ABCDEF的内角和为:180°×(6﹣2)=720°;
(2)∵六边形ABCDEF的内角和为720°,∠1+∠2+∠3+∠4+∠5=460°,
∴∠GBC+∠C+∠CDG=720°﹣460°=260°,
∴∠BGD=360°﹣(∠GBC+∠C+∠CDG)=100°.
即∠BGD的度数是100°.
20.【解答】解:依题意有n=4+3=7,
m=6+2=8,
(t﹣2)×180°=360°×4,
解得t=10,
则(n﹣m)t=(7﹣8)10=1.
21.【解答】解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
22.【解答】解:由图可得,
∠A+∠D+∠B+∠E+∠C+∠F的和正好是中间小三角形的三个外角之和,
∵三角形的外角和是360°,
∴∠A+∠D+∠B+∠E+∠C+∠F=360°.
23.【解答】解:(1)∵AD∥BC,
∴∠ADO=∠OBC.
∵1,
∴可设∠ODE=∠ADE=α,∠OCF=∠BCF=β.
∵AC⊥BD,
∴∠DOC=90°,
∴∠OBC+∠BCO=90°,
∴∠ADO+∠BCO=90°;
∴2α+2β=90°,
∴α+β=45°.
∵∠DEO=90°﹣α,∠CFO=90°﹣β,
∴∠DEO+∠CFO=90°﹣α+90°﹣β=180°﹣(α+β)=135°;
(2)∠AMD+∠BNC=180°∠DOC.理由如下:
∵AD∥BC,
∴∠ADO=∠OBC,∠DAB+∠ABC=180°.
∵2,
∴可设∠ADE=γ,∠BCF=θ,则∠ODE=2γ,∠OCF=2θ.
∵∠AMD+∠BNC=180°﹣∠DAB﹣γ+180°﹣∠ABC﹣θ=360°﹣(∠DAB+∠ABC)﹣(γ+θ)=180°﹣(γ+θ),
∠DOC=∠OBC+∠BCO=∠ADO+∠BCO=3γ+3θ=3(γ+θ),
∴∠AMD+∠BNC=180°∠DOC.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
