8.1.1认识三角形培优练习(含答案)
文档属性
| 名称 | 8.1.1认识三角形培优练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 477.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 17:53:18 | ||
图片预览



文档简介
8.1.1认识三角形培优练习华东师大版2024—2025学年七年级下册
一、选择题
1.如图,三角形的个数是( )
A.4个 B.3个
C.2个 D.1个
2.△ABC的三角之比是1:2:3,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
3.如图,在△ABC中,AB=7,AC=5,AD是△ABC的中线,则△ABD与△ADC的周长之差为( )
A.0 B.1
C.2 D.3
4.如图,下列图形中,AD是△ABC中BC边上的高的是( )
A.B. C.D.
5.如图,已知D是BC的中点,AE、AF分别是△ABC的角平分线、高线,则下列结论正确的是( )
A.AD=CD B.
C.∠AEB=90° D.DF=CF
二、填空题
6.如图,直线l经过A,B,C,D,E五点,点P是直线l外一点,连接PA,PB,PC,PD,PE,则共有 个三角形.
7.如图,已知AE为△ABC的中线,AB=8cm,AC=6cm,△ACE的周长为20cm,则△ABE的周长为 cm.
8.如图,AD、BE、CF是△ABC的三条中线,若△ABC的周长是10cm.则AE+CD+BF的长为 cm.
9.如图,在△ABC中,AD为中线,DE和DF分别为△ADB和△ADC的高,若AB=6,AC=8,DF=3,则DE= .
10.AD为△ABC的角平分线,DE∥AB交AC于E,若∠BAC=100°,则∠ADE= °.
三、解答题
11.如图,在△ABC中,点D在边BC上.
(1)若∠1=∠2=35°,∠3=∠4,求∠DAC的度数;
(2)若AD为△ABC的中线,△ABD的周长比△ACD的周长大3,AB=9,求AC的长.
12.如图,在△ABC中,BE是△ABC的角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是中线,BC=7,AC=5,则△BCD与△ACD的周长差为 ;
(2)若∠A=80°,CD是角平分线,求∠BOC= ;
(3)若∠ABC=62°,CD是高,求∠BOC的度数.
13.如图,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若∠BED=60°,∠BAD=40°,求∠BAF的度数.
(2)若AB=8,AC=6,求中线AD长的取值范围.
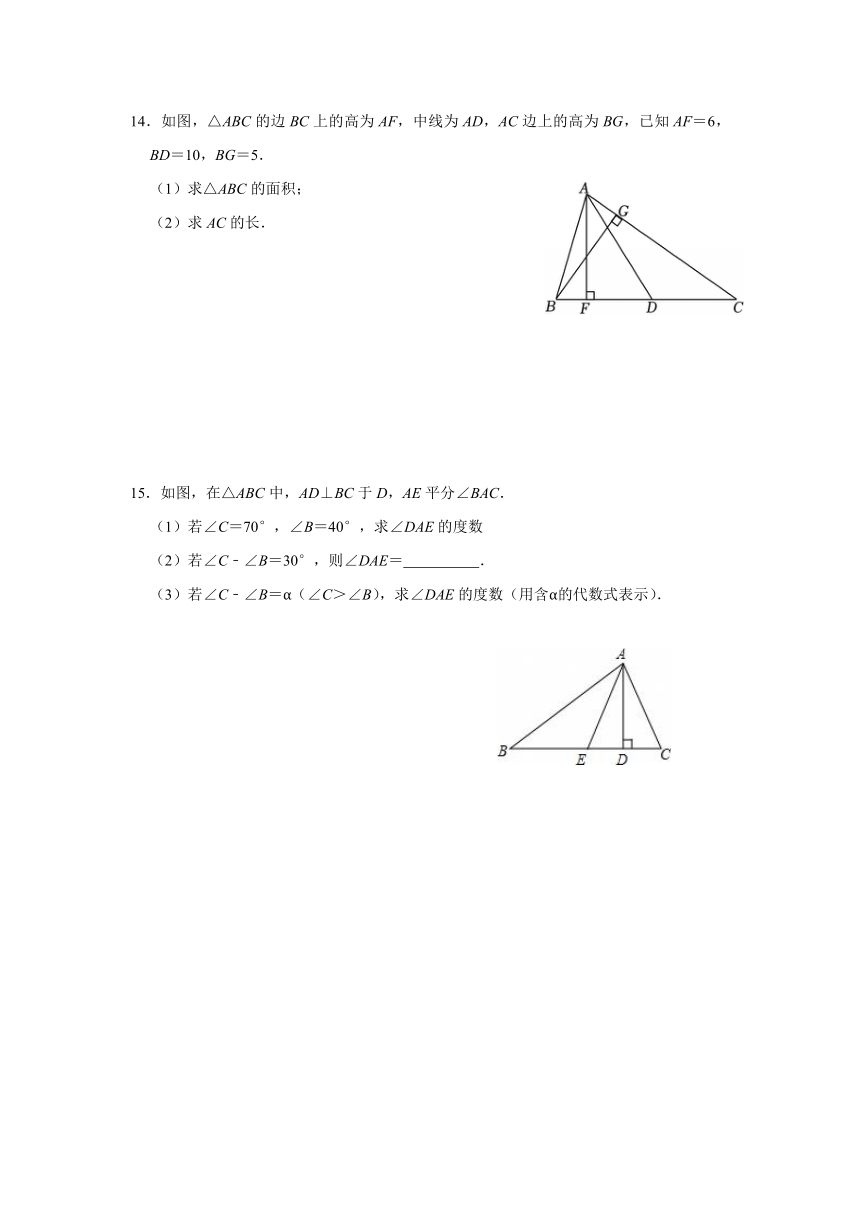
14.如图,△ABC的边BC上的高为AF,中线为AD,AC边上的高为BG,已知AF=6,BD=10,BG=5.
(1)求△ABC的面积;
(2)求AC的长.
15.如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=40°,求∠DAE的度数
(2)若∠C﹣∠B=30°,则∠DAE= .
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).
参考答案
一、选择题
题号 1 2 3 4 5
答案 B B C D B
二、填空题
6.【解答】解:△PAE,△PBE,△PCE,△PDE,△PAB,△PAC,△PAD,△PBC,△PBD,△PCD共10个,
故答案为:10.
7.【解答】解:∵AE为△ABC的中线,
∴BE=EC,
∵△ACE的周长为20cm,
∴AC+CE+AE=20cm,
∵AC=6cm,
∴CE+AE=14cm,
∴BE+AE=14cm,
∴△ABE的周长=AB+BE+AE=8+14=22(cm),
故答案为:22.
8.【解答】解:∵AD、BE、CF是△ABC的三条中线,
∴,
∴,
而△ABC的周长是10cm,
∴.
故答案为:5.
9.【解答】解:∵在△ABC中,AD为中线,
∴S△ABD=S△ACD,
∵DE和DF分别为△ADB和△ADC的高,
∴,即,
∴DE=4,
故答案为:4.
10.【解答】解:∵AD为△ABC的角平分线,∠BAC=100°,
∴∠BAD=∠CAD100°=50°,
∵DE∥AB,
∴∠ADE=∠BAD=50°.
故答案为50.
三、解答题
11.【解答】解:(1)∵∠1=∠2=35°,
∴∠3=∠1+∠2=70°,
∴∠3=∠4=70°,
∴∠DAC=180°﹣∠3﹣∠4=40°;
(2)∵AD为△ABC的中线,
∴BD=CD,
∵△ABD的周长比△ACD的周长大3,
∴AB+AD+BD﹣(AC+AD+CD)=3,
∴AB+AD+BD﹣AC﹣AD﹣CD=3,
∴AB﹣AC=3,
∵AB=9,
∴AC=6.
12.【解答】解:(1)∵CD是AB的中线,
∴AD=DB,
∵BC=7,AC=5,
∴△BCD与△ACD的周长差为:(BC+CD+BD)﹣(AC+CD+AD)=BC﹣AC=2,
故答案为:2;
(2)∵∠A=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵BE是△ABC的角平分线,CD是角平分线,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB(∠ABC+∠ACB)=50°,
∴∠BOC=180°﹣50°=130°,
故答案为:130;
(3)∵CD是高,
∴∠CDB=90°,
∵∠ABC=62°,
∴∠BCD=90°﹣62°=28°,
∵BE平分∠ABC,
∴,
在△BOC中,∠BOC=180°﹣28°﹣31°=121°.
13.【解答】解:(1)∵∠BED=∠ABE+∠BAE,∠BED=60°,∠BAD=40°,
∴∠ABE=60°﹣40°=20°,
∵BE平分∠ABC,
∴∠ABC=2∠ABE=40°,
∵AF为高,
∴∠AFB=90°,
∴∠BAF=90°﹣∠ABF=90°﹣40°=50°;
(2)延长AD至K,使AD=DK,连接CK.
∵AD是△ABC的中线,
∴BD=CD,
∵∠ADB=∠CDK,
∴△ADB≌△KDC,
∴AB=CK=8,而AC=6,
∴2<AK<14,
∴1<AD<7.
14.【解答】解:(1)∵△ABC的边BC上的高为AF,中线为AD,AF=6,BD=10,
∴BC=2BD=20,
△ABC的面积;
(2)∵△ABC的面积,
∵BG=5,
∴AC=24.
15.【解答】解:(1)由已知可得,∠BAC=180°﹣40°﹣70°=70°,
∴∠CAD=20°,
∴∠DAE=∠CAE﹣∠CAD=35°﹣20°=15°;
(2)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE∠BAC(180°﹣∠B﹣∠C)=90°(∠B+∠C),
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAD﹣∠BAE=(90°﹣∠B)﹣[90°(∠B+∠C)](∠C﹣∠B),
∵∠C﹣∠B=30°,
∴∠DAE30°=15°,
故答案为:15°;
(3)∵∠C﹣∠B=α,
∴∠DAEα.
一、选择题
1.如图,三角形的个数是( )
A.4个 B.3个
C.2个 D.1个
2.△ABC的三角之比是1:2:3,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
3.如图,在△ABC中,AB=7,AC=5,AD是△ABC的中线,则△ABD与△ADC的周长之差为( )
A.0 B.1
C.2 D.3
4.如图,下列图形中,AD是△ABC中BC边上的高的是( )
A.B. C.D.
5.如图,已知D是BC的中点,AE、AF分别是△ABC的角平分线、高线,则下列结论正确的是( )
A.AD=CD B.
C.∠AEB=90° D.DF=CF
二、填空题
6.如图,直线l经过A,B,C,D,E五点,点P是直线l外一点,连接PA,PB,PC,PD,PE,则共有 个三角形.
7.如图,已知AE为△ABC的中线,AB=8cm,AC=6cm,△ACE的周长为20cm,则△ABE的周长为 cm.
8.如图,AD、BE、CF是△ABC的三条中线,若△ABC的周长是10cm.则AE+CD+BF的长为 cm.
9.如图,在△ABC中,AD为中线,DE和DF分别为△ADB和△ADC的高,若AB=6,AC=8,DF=3,则DE= .
10.AD为△ABC的角平分线,DE∥AB交AC于E,若∠BAC=100°,则∠ADE= °.
三、解答题
11.如图,在△ABC中,点D在边BC上.
(1)若∠1=∠2=35°,∠3=∠4,求∠DAC的度数;
(2)若AD为△ABC的中线,△ABD的周长比△ACD的周长大3,AB=9,求AC的长.
12.如图,在△ABC中,BE是△ABC的角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是中线,BC=7,AC=5,则△BCD与△ACD的周长差为 ;
(2)若∠A=80°,CD是角平分线,求∠BOC= ;
(3)若∠ABC=62°,CD是高,求∠BOC的度数.
13.如图,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若∠BED=60°,∠BAD=40°,求∠BAF的度数.
(2)若AB=8,AC=6,求中线AD长的取值范围.
14.如图,△ABC的边BC上的高为AF,中线为AD,AC边上的高为BG,已知AF=6,BD=10,BG=5.
(1)求△ABC的面积;
(2)求AC的长.
15.如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=40°,求∠DAE的度数
(2)若∠C﹣∠B=30°,则∠DAE= .
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).
参考答案
一、选择题
题号 1 2 3 4 5
答案 B B C D B
二、填空题
6.【解答】解:△PAE,△PBE,△PCE,△PDE,△PAB,△PAC,△PAD,△PBC,△PBD,△PCD共10个,
故答案为:10.
7.【解答】解:∵AE为△ABC的中线,
∴BE=EC,
∵△ACE的周长为20cm,
∴AC+CE+AE=20cm,
∵AC=6cm,
∴CE+AE=14cm,
∴BE+AE=14cm,
∴△ABE的周长=AB+BE+AE=8+14=22(cm),
故答案为:22.
8.【解答】解:∵AD、BE、CF是△ABC的三条中线,
∴,
∴,
而△ABC的周长是10cm,
∴.
故答案为:5.
9.【解答】解:∵在△ABC中,AD为中线,
∴S△ABD=S△ACD,
∵DE和DF分别为△ADB和△ADC的高,
∴,即,
∴DE=4,
故答案为:4.
10.【解答】解:∵AD为△ABC的角平分线,∠BAC=100°,
∴∠BAD=∠CAD100°=50°,
∵DE∥AB,
∴∠ADE=∠BAD=50°.
故答案为50.
三、解答题
11.【解答】解:(1)∵∠1=∠2=35°,
∴∠3=∠1+∠2=70°,
∴∠3=∠4=70°,
∴∠DAC=180°﹣∠3﹣∠4=40°;
(2)∵AD为△ABC的中线,
∴BD=CD,
∵△ABD的周长比△ACD的周长大3,
∴AB+AD+BD﹣(AC+AD+CD)=3,
∴AB+AD+BD﹣AC﹣AD﹣CD=3,
∴AB﹣AC=3,
∵AB=9,
∴AC=6.
12.【解答】解:(1)∵CD是AB的中线,
∴AD=DB,
∵BC=7,AC=5,
∴△BCD与△ACD的周长差为:(BC+CD+BD)﹣(AC+CD+AD)=BC﹣AC=2,
故答案为:2;
(2)∵∠A=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵BE是△ABC的角平分线,CD是角平分线,
∴∠OBC∠ABC,∠OCB∠ACB,
∴∠OBC+∠OCB(∠ABC+∠ACB)=50°,
∴∠BOC=180°﹣50°=130°,
故答案为:130;
(3)∵CD是高,
∴∠CDB=90°,
∵∠ABC=62°,
∴∠BCD=90°﹣62°=28°,
∵BE平分∠ABC,
∴,
在△BOC中,∠BOC=180°﹣28°﹣31°=121°.
13.【解答】解:(1)∵∠BED=∠ABE+∠BAE,∠BED=60°,∠BAD=40°,
∴∠ABE=60°﹣40°=20°,
∵BE平分∠ABC,
∴∠ABC=2∠ABE=40°,
∵AF为高,
∴∠AFB=90°,
∴∠BAF=90°﹣∠ABF=90°﹣40°=50°;
(2)延长AD至K,使AD=DK,连接CK.
∵AD是△ABC的中线,
∴BD=CD,
∵∠ADB=∠CDK,
∴△ADB≌△KDC,
∴AB=CK=8,而AC=6,
∴2<AK<14,
∴1<AD<7.
14.【解答】解:(1)∵△ABC的边BC上的高为AF,中线为AD,AF=6,BD=10,
∴BC=2BD=20,
△ABC的面积;
(2)∵△ABC的面积,
∵BG=5,
∴AC=24.
15.【解答】解:(1)由已知可得,∠BAC=180°﹣40°﹣70°=70°,
∴∠CAD=20°,
∴∠DAE=∠CAE﹣∠CAD=35°﹣20°=15°;
(2)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE∠BAC(180°﹣∠B﹣∠C)=90°(∠B+∠C),
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAD﹣∠BAE=(90°﹣∠B)﹣[90°(∠B+∠C)](∠C﹣∠B),
∵∠C﹣∠B=30°,
∴∠DAE30°=15°,
故答案为:15°;
(3)∵∠C﹣∠B=α,
∴∠DAEα.
