8.1.2三角形的内角和与外角和培优练习(含答案)
文档属性
| 名称 | 8.1.2三角形的内角和与外角和培优练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 537.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 17:53:45 | ||
图片预览

文档简介
8.1.2三角形的内角和与外角和培优练习华东师大版2024—2025学年七年级下册
一、选择题
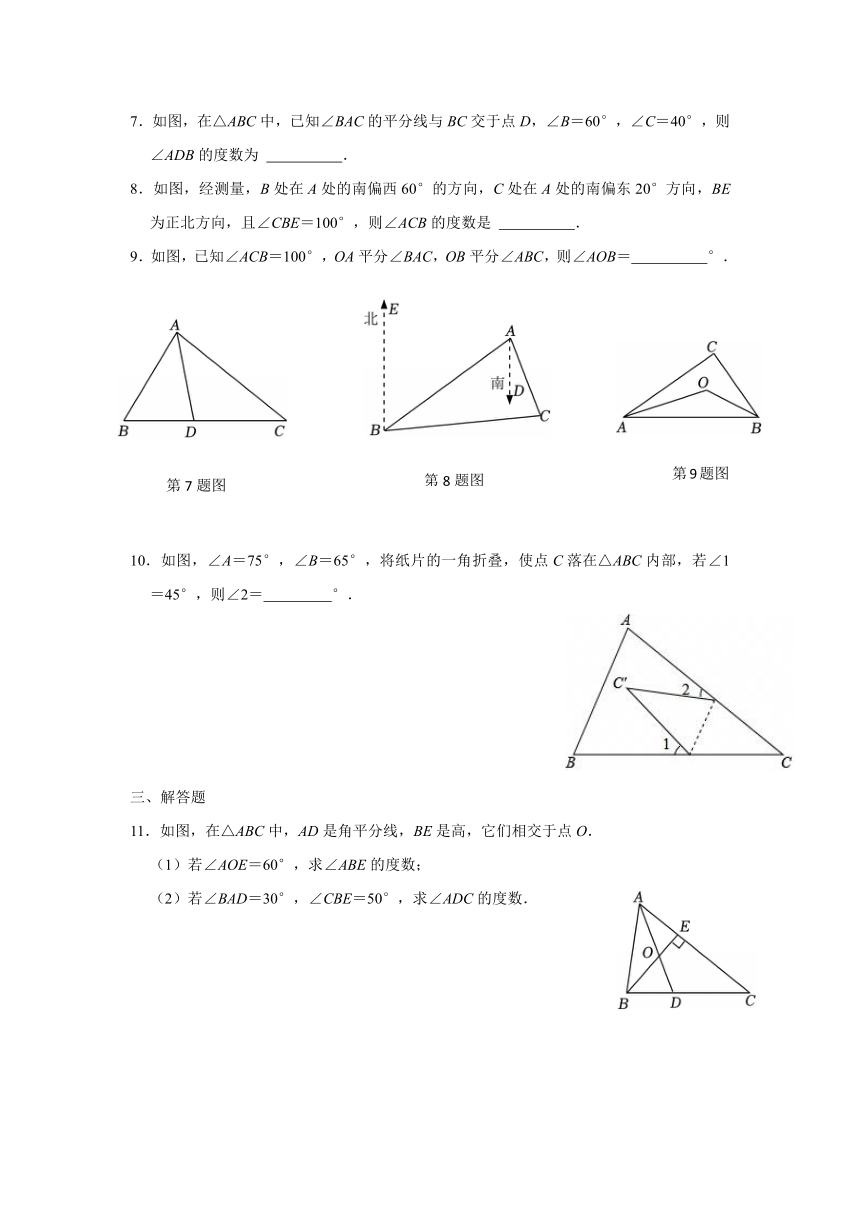
1.如图,△ABC中∠B=40°,∠C=30°,延长BA到点D,则∠CAD的度数是( )
A.50° B.70° C.80° D.110°
2.如图,在△ABC中,点D在边AC上(不与端点重合),连接BD.则∠1,∠2,∠3的大小关系是( )
A.∠1<∠2<∠3 B.∠1<∠3<∠2 C.∠3<∠2<∠1 D.∠2<∠1<∠3
3.一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
4.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,∠BAC=60°,∠C=70°,则∠DAE的度数为( )
A.15° B.8° C.10° D.12°
5.如图,∠ABC的平分线与∠ACB的外角平分线相交于D,∠D=40°,则∠A等于( )
A.50° B.60° C.70° D.80°
二、填空题
6.如图,将一条对边互相平行的纸带与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是 .
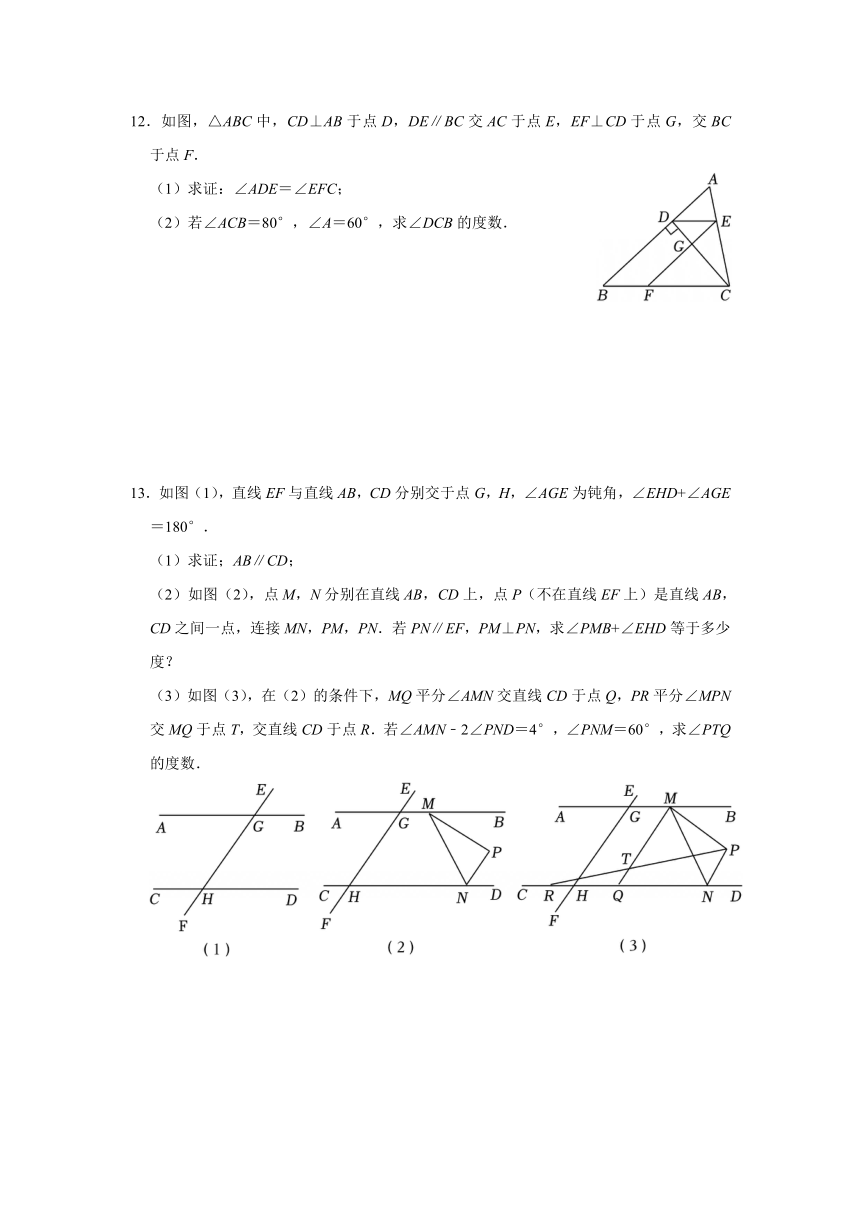
7.如图,在△ABC中,已知∠BAC的平分线与BC交于点D,∠B=60°,∠C=40°,则∠ADB的度数为 .
8.如图,经测量,B处在A处的南偏西60°的方向,C处在A处的南偏东20°方向,BE为正北方向,且∠CBE=100°,则∠ACB的度数是 .
9.如图,已知∠ACB=100°,OA平分∠BAC,OB平分∠ABC,则∠AOB= °.
10.如图,∠A=75°,∠B=65°,将纸片的一角折叠,使点C落在△ABC内部,若∠1=45°,则∠2= °.
三、解答题
11.如图,在△ABC中,AD是角平分线,BE是高,它们相交于点O.
(1)若∠AOE=60°,求∠ABE的度数;
(2)若∠BAD=30°,∠CBE=50°,求∠ADC的度数.
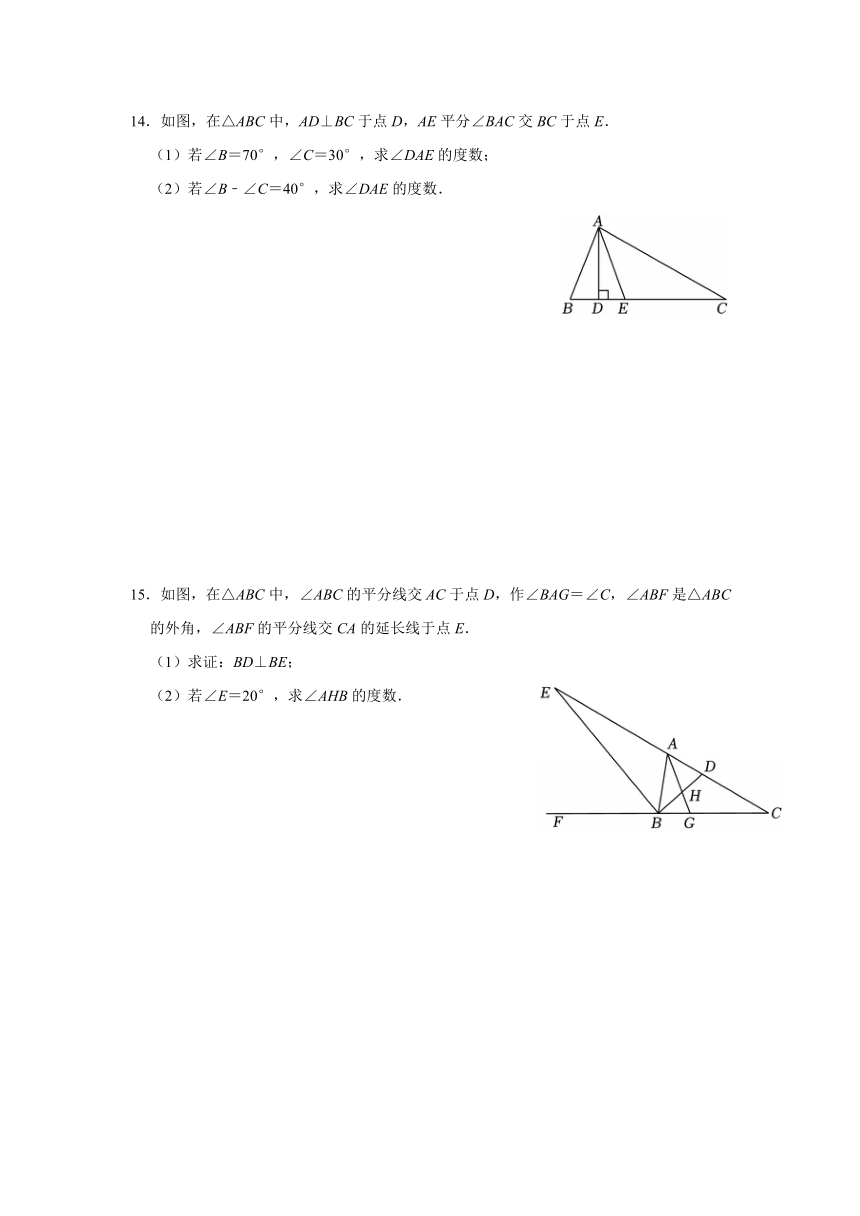
12.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=80°,∠A=60°,求∠DCB的度数.
13.如图(1),直线EF与直线AB,CD分别交于点G,H,∠AGE为钝角,∠EHD+∠AGE=180°.
(1)求证;AB∥CD;
(2)如图(2),点M,N分别在直线AB,CD上,点P(不在直线EF上)是直线AB,CD之间一点,连接MN,PM,PN.若PN∥EF,PM⊥PN,求∠PMB+∠EHD等于多少度?
(3)如图(3),在(2)的条件下,MQ平分∠AMN交直线CD于点Q,PR平分∠MPN交MQ于点T,交直线CD于点R.若∠AMN﹣2∠PND=4°,∠PNM=60°,求∠PTQ 的度数.
14.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC交BC于点E.
(1)若∠B=70°,∠C=30°,求∠DAE的度数;
(2)若∠B﹣∠C=40°,求∠DAE的度数.
15.如图,在△ABC中,∠ABC的平分线交AC于点D,作∠BAG=∠C,∠ABF是△ABC的外角,∠ABF的平分线交CA的延长线于点E.
(1)求证:BD⊥BE;
(2)若∠E=20°,求∠AHB的度数.
参考答案
一、选择题
题号 1 2 3 4 5
答案 B A D C D
二、解答题
6.【解答】解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°.
故答案为:50°.
7.【解答】解:∵∠B=60°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∵AD平分∠BAC,
∴∠DAC∠BAC=40°
∴∠ADB=∠C+∠DAC=80°.
故答案为:80°.
8.【解答】解:由题意得:
∠DAB=60°,∠CAD=20°,BE∥AD,
∴∠EBA=∠DAB=60°,
∵∠CBE=100°,
∴∠ABC=∠CBE﹣∠EBA=40°,
∵∠CAB=∠BAD+∠CAD=80°,
∴∠ACB=180°﹣∠CAB﹣∠ABC=60°,
故答案为:60°.
9.【解答】解:∵OA平分∠BAC,OB平分∠ABC,
∴∠OABCAB,∠OBA∠CBA.
∵∠AOB=180°﹣∠OAB﹣∠OBA
=180°∠CAB∠CBA
=180°(∠CAB+∠CBA)
=180°(180°﹣∠ACB)
=90°∠ACB.
当∠ACB=100°时,
∠AOB=90°100°
=140°.
故答案为:140°.
10.【解答】解:如图,
由折叠的性质可得∠CDE=∠C'DE,∠CED=∠C'ED,
∵∠A=75°,∠B=65°,
∴∠C=180°﹣(65°+75°)=40°,
∴∠CDE+∠CED=180°﹣∠C=140°,
∴∠2=360°﹣(∠A+∠B+∠1+∠CED+∠CDE)=360°﹣325°=35°.
故答案为:35.
三、参考答案
11.【解答】解:(1)由条件可知∠BEA=90°,
又∵∠AOE=60°,
∴∠DAE=90°﹣∠AOE=30°,
∵AD是角平分线,
∴∠BAE=2∠DAE=60°,
∴∠ABE=90°﹣∠BAE=30°
∴∠ABE的度数为30°.
(2)由条件可知∠BEC=90°,
又∵∠CBE=50°,
∴∠C=90°﹣∠CBE=40°,
∵AD是角平分线,
∴∠CAD=∠BAD=30°,
∴∠ADC=180°﹣∠C﹣∠CAD=110°.
∴∠ADC的度数为110°.
12.【解答】(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)解:∵∠ACB=80°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=40°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣40°=50°.
13.【解答】(1)证明:∵直线AB与直线EF交于点G,
∴∠AGE=∠BGF,
又∵∠EHD+∠AGE=180°,
∴∠EHD+∠BGF=180°,
∴AB∥CD;
(2)过点P作PK∥AB,如图所示:
由(1)可知:AB∥CD,
∴AB∥PK∥CD,
∴∠PMB=∠MPK,∠PND=∠NPK,
∴∠PMB+∠PND=∠MPK+∠NPK=∠MPN,
∵PM⊥PN,
∴∠MPN=90°,
∴∠PMB+∠PND=90°,
∵PN∥EF,
∴∠EHD=∠PND,
∴∠PMB+∠EHD=90°;
(3)设∠AMQ=α,
∵MQ平分∠AMN,
∴∠AMQ=∠QMN=α,
∴∠AMN=2α,
∵PM⊥PN,∠PNM=60°,
∴∠PMN=90°﹣60°=30°,
∴∠QMP=∠QMN+∠PMN=α+30°,
∠PMB=180°﹣∠AMN﹣∠PMN=180°﹣2α﹣30°=150°﹣2α,
由(2)可知:∠PMB+∠PND=90°,
∴∠PND=90°﹣∠PMB=90°﹣(150°﹣2α)=2α﹣60°,
∵∠AMN﹣2∠PND=4°,
∴2α﹣2(2α﹣60°)=4°,
解得:α=58°,
∴∠QMP=α+30°=88°,
∵PM⊥PN,PR平分∠MPN,
∴∠MPT=45°,
∴∠PTQ=∠QMP+∠MPT=45°+88°=133°.
14.【解答】解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,
∵AE平分∠BAC,
∴∠BAE∠BAC=40°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠BAD=90°﹣∠B=90°﹣70°=20°;
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;
(2)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE∠BAC(180°﹣∠B﹣∠C)=90°(∠B+∠C),
∵AD⊥BC,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°(∠B+∠C)﹣(90°﹣∠B)(∠B﹣∠C).
又∵∠B﹣∠C=40°,
∴∠DAE40°=20°.
15.【解答】(1)证明:∵∠ABC的平分线交AC于点D,∠ABF的平分线交CA的延长线于点E,
∴∠ABD∠ABC,∠ABE∠ABF,
∵∠ABC+∠ABF=180°,
∴∠ABD+∠ABE(∠ABC+∠ABF)=90°,即BD⊥BE;
(2)解:由(1)知BD⊥BE,∠CBD=∠DBA,
∴∠DBE=90°,
∵∠E=20°,
∴∠BDE=90°﹣20°=70°,
∴∠C+∠CBD=∠BDE=70°,
∵∠BAG=∠C,∠CBD=∠DBA,
∴∠DBA+∠BAG=70°,
∴∠AHB=180°﹣70°=110°.
一、选择题
1.如图,△ABC中∠B=40°,∠C=30°,延长BA到点D,则∠CAD的度数是( )
A.50° B.70° C.80° D.110°
2.如图,在△ABC中,点D在边AC上(不与端点重合),连接BD.则∠1,∠2,∠3的大小关系是( )
A.∠1<∠2<∠3 B.∠1<∠3<∠2 C.∠3<∠2<∠1 D.∠2<∠1<∠3
3.一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
4.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,∠BAC=60°,∠C=70°,则∠DAE的度数为( )
A.15° B.8° C.10° D.12°
5.如图,∠ABC的平分线与∠ACB的外角平分线相交于D,∠D=40°,则∠A等于( )
A.50° B.60° C.70° D.80°
二、填空题
6.如图,将一条对边互相平行的纸带与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是 .
7.如图,在△ABC中,已知∠BAC的平分线与BC交于点D,∠B=60°,∠C=40°,则∠ADB的度数为 .
8.如图,经测量,B处在A处的南偏西60°的方向,C处在A处的南偏东20°方向,BE为正北方向,且∠CBE=100°,则∠ACB的度数是 .
9.如图,已知∠ACB=100°,OA平分∠BAC,OB平分∠ABC,则∠AOB= °.
10.如图,∠A=75°,∠B=65°,将纸片的一角折叠,使点C落在△ABC内部,若∠1=45°,则∠2= °.
三、解答题
11.如图,在△ABC中,AD是角平分线,BE是高,它们相交于点O.
(1)若∠AOE=60°,求∠ABE的度数;
(2)若∠BAD=30°,∠CBE=50°,求∠ADC的度数.
12.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=80°,∠A=60°,求∠DCB的度数.
13.如图(1),直线EF与直线AB,CD分别交于点G,H,∠AGE为钝角,∠EHD+∠AGE=180°.
(1)求证;AB∥CD;
(2)如图(2),点M,N分别在直线AB,CD上,点P(不在直线EF上)是直线AB,CD之间一点,连接MN,PM,PN.若PN∥EF,PM⊥PN,求∠PMB+∠EHD等于多少度?
(3)如图(3),在(2)的条件下,MQ平分∠AMN交直线CD于点Q,PR平分∠MPN交MQ于点T,交直线CD于点R.若∠AMN﹣2∠PND=4°,∠PNM=60°,求∠PTQ 的度数.
14.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC交BC于点E.
(1)若∠B=70°,∠C=30°,求∠DAE的度数;
(2)若∠B﹣∠C=40°,求∠DAE的度数.
15.如图,在△ABC中,∠ABC的平分线交AC于点D,作∠BAG=∠C,∠ABF是△ABC的外角,∠ABF的平分线交CA的延长线于点E.
(1)求证:BD⊥BE;
(2)若∠E=20°,求∠AHB的度数.
参考答案
一、选择题
题号 1 2 3 4 5
答案 B A D C D
二、解答题
6.【解答】解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°.
故答案为:50°.
7.【解答】解:∵∠B=60°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∵AD平分∠BAC,
∴∠DAC∠BAC=40°
∴∠ADB=∠C+∠DAC=80°.
故答案为:80°.
8.【解答】解:由题意得:
∠DAB=60°,∠CAD=20°,BE∥AD,
∴∠EBA=∠DAB=60°,
∵∠CBE=100°,
∴∠ABC=∠CBE﹣∠EBA=40°,
∵∠CAB=∠BAD+∠CAD=80°,
∴∠ACB=180°﹣∠CAB﹣∠ABC=60°,
故答案为:60°.
9.【解答】解:∵OA平分∠BAC,OB平分∠ABC,
∴∠OABCAB,∠OBA∠CBA.
∵∠AOB=180°﹣∠OAB﹣∠OBA
=180°∠CAB∠CBA
=180°(∠CAB+∠CBA)
=180°(180°﹣∠ACB)
=90°∠ACB.
当∠ACB=100°时,
∠AOB=90°100°
=140°.
故答案为:140°.
10.【解答】解:如图,
由折叠的性质可得∠CDE=∠C'DE,∠CED=∠C'ED,
∵∠A=75°,∠B=65°,
∴∠C=180°﹣(65°+75°)=40°,
∴∠CDE+∠CED=180°﹣∠C=140°,
∴∠2=360°﹣(∠A+∠B+∠1+∠CED+∠CDE)=360°﹣325°=35°.
故答案为:35.
三、参考答案
11.【解答】解:(1)由条件可知∠BEA=90°,
又∵∠AOE=60°,
∴∠DAE=90°﹣∠AOE=30°,
∵AD是角平分线,
∴∠BAE=2∠DAE=60°,
∴∠ABE=90°﹣∠BAE=30°
∴∠ABE的度数为30°.
(2)由条件可知∠BEC=90°,
又∵∠CBE=50°,
∴∠C=90°﹣∠CBE=40°,
∵AD是角平分线,
∴∠CAD=∠BAD=30°,
∴∠ADC=180°﹣∠C﹣∠CAD=110°.
∴∠ADC的度数为110°.
12.【解答】(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)解:∵∠ACB=80°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=40°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣40°=50°.
13.【解答】(1)证明:∵直线AB与直线EF交于点G,
∴∠AGE=∠BGF,
又∵∠EHD+∠AGE=180°,
∴∠EHD+∠BGF=180°,
∴AB∥CD;
(2)过点P作PK∥AB,如图所示:
由(1)可知:AB∥CD,
∴AB∥PK∥CD,
∴∠PMB=∠MPK,∠PND=∠NPK,
∴∠PMB+∠PND=∠MPK+∠NPK=∠MPN,
∵PM⊥PN,
∴∠MPN=90°,
∴∠PMB+∠PND=90°,
∵PN∥EF,
∴∠EHD=∠PND,
∴∠PMB+∠EHD=90°;
(3)设∠AMQ=α,
∵MQ平分∠AMN,
∴∠AMQ=∠QMN=α,
∴∠AMN=2α,
∵PM⊥PN,∠PNM=60°,
∴∠PMN=90°﹣60°=30°,
∴∠QMP=∠QMN+∠PMN=α+30°,
∠PMB=180°﹣∠AMN﹣∠PMN=180°﹣2α﹣30°=150°﹣2α,
由(2)可知:∠PMB+∠PND=90°,
∴∠PND=90°﹣∠PMB=90°﹣(150°﹣2α)=2α﹣60°,
∵∠AMN﹣2∠PND=4°,
∴2α﹣2(2α﹣60°)=4°,
解得:α=58°,
∴∠QMP=α+30°=88°,
∵PM⊥PN,PR平分∠MPN,
∴∠MPT=45°,
∴∠PTQ=∠QMP+∠MPT=45°+88°=133°.
14.【解答】解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,
∵AE平分∠BAC,
∴∠BAE∠BAC=40°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠BAD=90°﹣∠B=90°﹣70°=20°;
∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;
(2)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C,
∵AE平分∠BAC,
∴∠BAE∠BAC(180°﹣∠B﹣∠C)=90°(∠B+∠C),
∵AD⊥BC,
∴∠BAD=90°﹣∠B,
∴∠DAE=∠BAE﹣∠BAD=90°(∠B+∠C)﹣(90°﹣∠B)(∠B﹣∠C).
又∵∠B﹣∠C=40°,
∴∠DAE40°=20°.
15.【解答】(1)证明:∵∠ABC的平分线交AC于点D,∠ABF的平分线交CA的延长线于点E,
∴∠ABD∠ABC,∠ABE∠ABF,
∵∠ABC+∠ABF=180°,
∴∠ABD+∠ABE(∠ABC+∠ABF)=90°,即BD⊥BE;
(2)解:由(1)知BD⊥BE,∠CBD=∠DBA,
∴∠DBE=90°,
∵∠E=20°,
∴∠BDE=90°﹣20°=70°,
∴∠C+∠CBD=∠BDE=70°,
∵∠BAG=∠C,∠CBD=∠DBA,
∴∠DBA+∠BAG=70°,
∴∠AHB=180°﹣70°=110°.
