8.2多边形的内角和与外角和培优练习(含答案)
文档属性
| 名称 | 8.2多边形的内角和与外角和培优练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 543.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 00:00:00 | ||
图片预览

文档简介
8.2多边形的内角和与外角和培优练习华东师大版2024—2025学年七年级下册
一.选择题
1.若n边形的内角和等于它外角和的2倍,则边数n为( )
A.7 B.6 C.5 D.4
2.从n边形的一个顶点出发,可以作6条对角线,则n的值是( )
A.12 B.10 C.9 D.8
3.如图,顺次连接图中六个点,得到以下图形,则∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.270° C.360° D.720°
4.已知∠EOF=90°,现将一直角三角板ABC(∠A=30°、∠C=90°)按如图所示的位置摆放,则∠α+∠β=( )
A.210° B.200° C.190° D.180°
5.若一个多边形截去一个角后,变成五边形,则原来的多边形的边数可能为( )
A.5或6 B.4或5 C.3或4或5 D.4或5或6
二.填空题
6.如图,将五角星沿着虚线FG剪下.若∠B+∠C+∠D+∠E=5∠A,则∠CFG+∠DGF= .
7.一个多边形的每个内角均为108°,则这个多边形的边数为 .
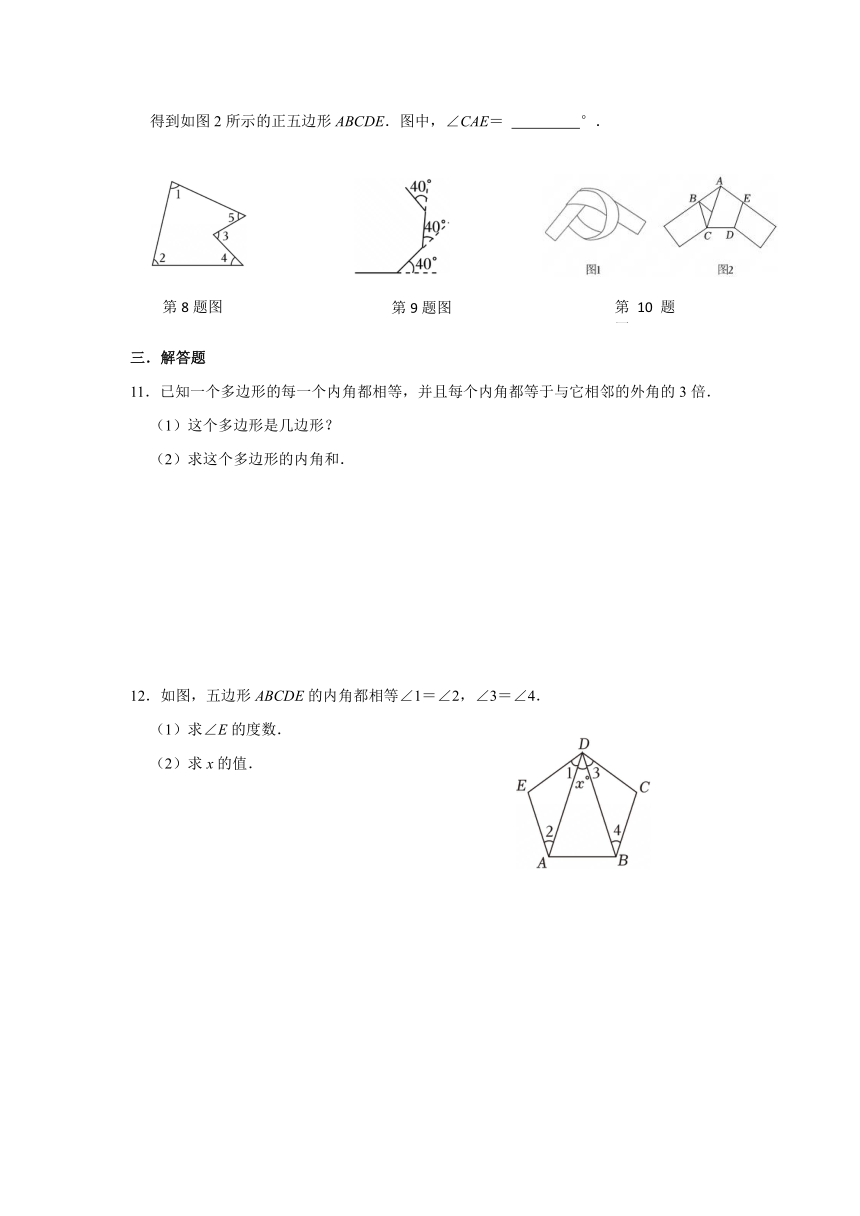
8.如图,∠1=65°,∠2=85°,∠3=60°,∠4=40°,则∠5= .
9.如图,小明在操场上从A点出发,沿直线前进8米后向左转40°,再沿直线前进8米后,又向左转40°,这样走下去,他第一次回到出发地A点时,一共走了 米.
10.用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠CAE= °.
三.解答题
11.已知一个多边形的每一个内角都相等,并且每个内角都等于与它相邻的外角的3倍.
(1)这个多边形是几边形?
(2)求这个多边形的内角和.
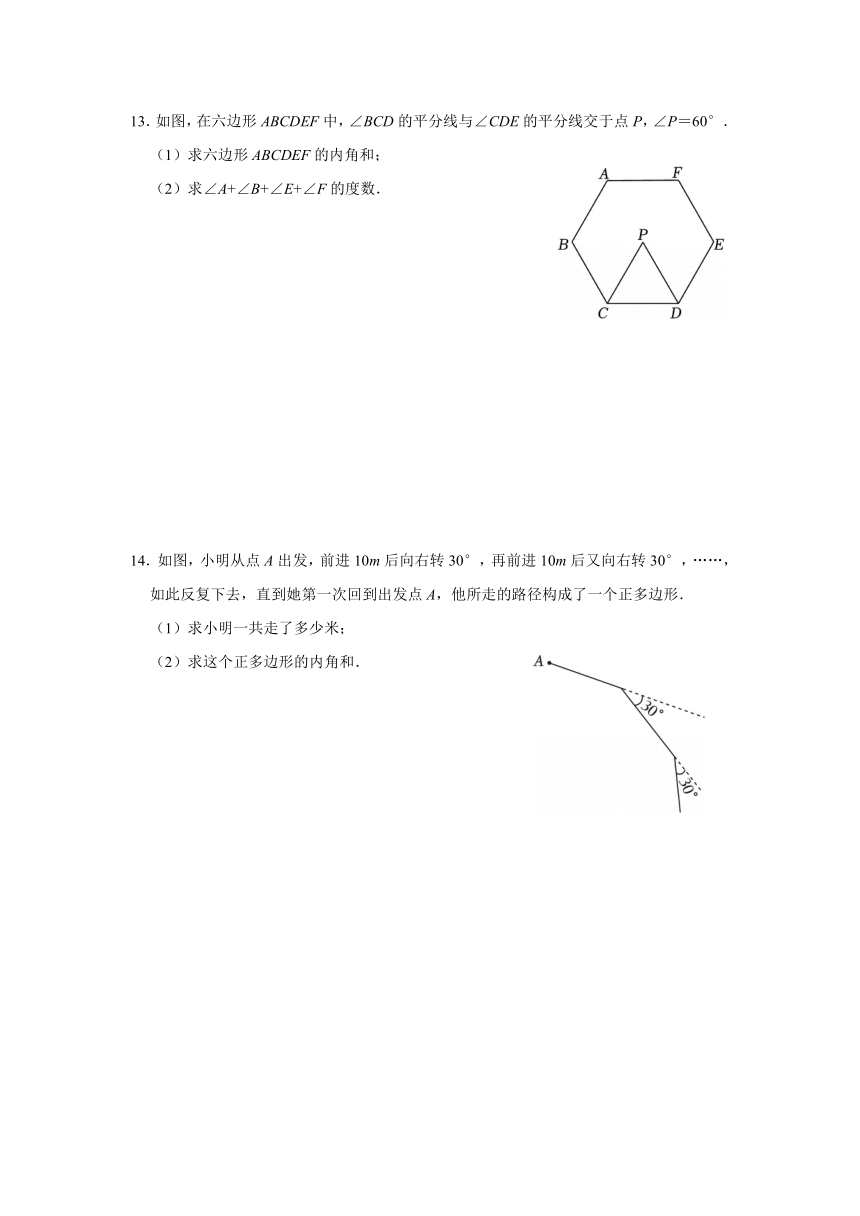
12.如图,五边形ABCDE的内角都相等∠1=∠2,∠3=∠4.
(1)求∠E的度数.
(2)求x的值.
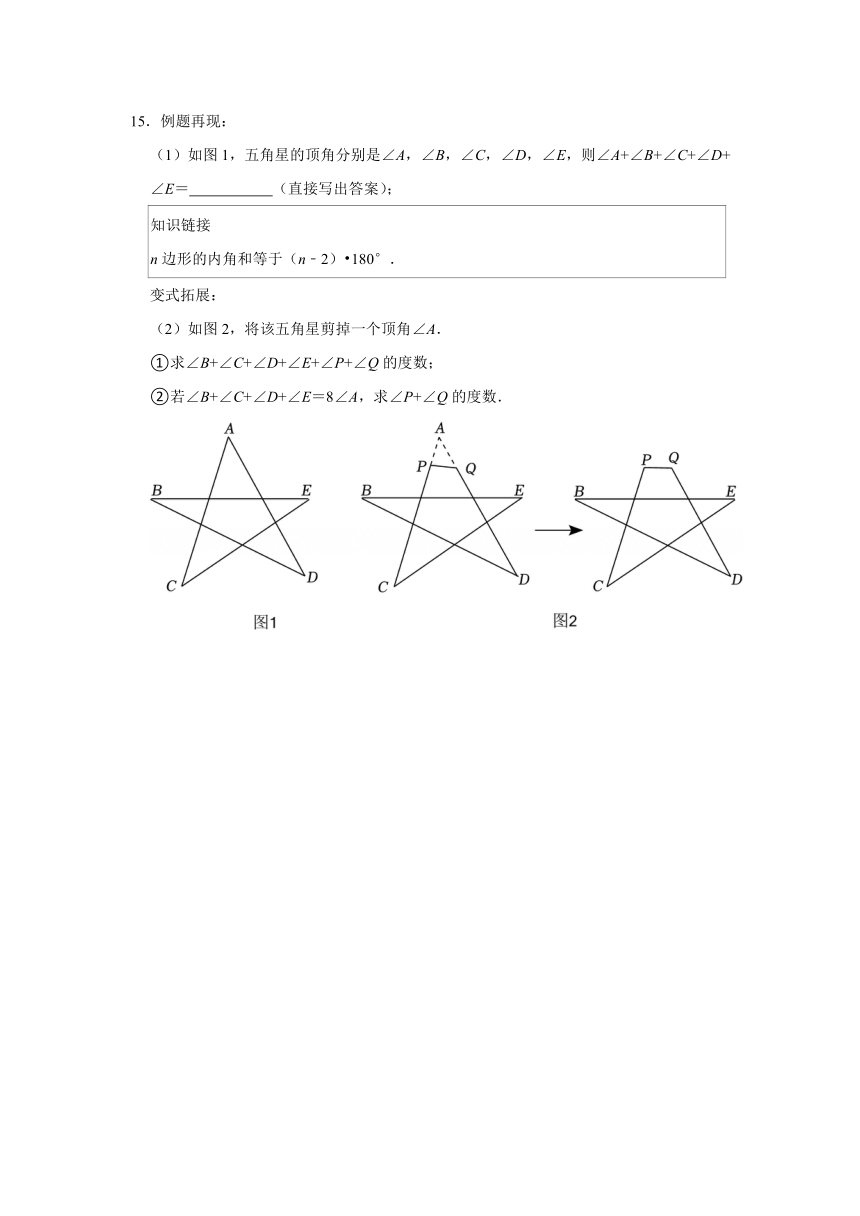
13.如图,在六边形ABCDEF中,∠BCD的平分线与∠CDE的平分线交于点P,∠P=60°.
(1)求六边形ABCDEF的内角和;
(2)求∠A+∠B+∠E+∠F的度数.
14.如图,小明从点A出发,前进10m后向右转30°,再前进10m后又向右转30°,……,如此反复下去,直到她第一次回到出发点A,他所走的路径构成了一个正多边形.
(1)求小明一共走了多少米;
(2)求这个正多边形的内角和.
15.例题再现:
(1)如图1,五角星的顶角分别是∠A,∠B,∠C,∠D,∠E,则∠A+∠B+∠C+∠D+∠E= (直接写出答案);
知识链接 n边形的内角和等于(n﹣2) 180°.
变式拓展:
(2)如图2,将该五角星剪掉一个顶角∠A.
①求∠B+∠C+∠D+∠E+∠P+∠Q的度数;
②若∠B+∠C+∠D+∠E=8∠A,求∠P+∠Q的度数.
参考答案
一、选择题
题号 1 2 3 4 5
答案 B C C A D
二、填空题
6.【解答】解:如图,∵∠AMN=∠C+∠E,∠ANM=∠B+∠D,而∠AMN+∠ANM+∠A=180°,
∴∠C+∠E+∠B+∠D=180°﹣∠A,
即∠A+∠B+∠C+∠D+∠E=180°,
又∵∠B+∠C+∠D+∠E=5∠A,
∴∠A+5∠A=180°,
解得∠A=30°,
∴∠CFG+∠DGF=∠AFG+∠AGF+∠A+∠A=180°+30°=210°,
故答案为:210°.
7.【解答】解:180°﹣108°=72°,
360°÷72°=5,
故答案为:5.
8.【解答】解:如图,连接BC,
在△BCE中,∠3+∠EBC+∠ECB=180°,
∵∠3=60°,
∴∠EBC+∠ECB=120°,
在四边形ABCD中,∠1+∠2+∠4+∠EBC+∠ECB+∠5=(4﹣2)×180°=360°,
∵∠1=65°,∠2=85°,∠4=40°,
∴65°+85°+40°+120°+∠5=360°,
∴∠5=50°,
故答案为:50°.
9.【解答】解:∵小明需要转360÷40=9次才会回到原点,
∴小明共走了9×8=72(米),
故答案为:72.
10.【解答】解:∵五边形ABCDE是正五边形,
∴∠ABC=∠BAE,AB=BC,
∴∠BAC=∠ACB,
∵∠ABC+∠BAC+∠ACB=180°,
∴∠BAC=∠ACB=36°,
∵∠BAE=∠BAC+∠CAE,
∴∠CAE=∠BAE﹣∠BAC=108°﹣36°=72°,
故答案为:72.
三、解答题
11.【解答】解:(1)设这个多边形的每个外角都为x°,则与它相邻的内角为3x°,由题意得:
x+3x=180,
4x=180,
x=45,
∴这个多边形的边数为:360÷45=8,
∴这个多边形是八边形;
(2)由(1)可知这个多边形是八边形,
∴这个多边形的内角和为:
(8﹣2)×180°=6×180°=1080°.
12.【解答】解:(1)由条件可知;
(2)由(1)可知∠CDE=∠E=108°,
∴,
同理∠3=36°,
∴∠ADB=∠CDE﹣∠1﹣∠3=108°﹣36°﹣36°=36°,
∴x=36.
13.【解答】解:(1)六边形ABCDEF的内角和=(6﹣2)×180°=720°;
(2)∵∠P=60°,
∴∠PCD+∠PDC=180°﹣∠P=180°﹣60°=120°,
∵PC平分∠BCD,PD平分∠EDC,
∴∠BCD+∠EDC=2∠PCD+2∠PDC=2×120°=240°,
∵∠A+∠B+∠E+∠F+∠BCD+∠EDC=720°,
∴∠A+∠B+∠E+∠F=720°﹣∠BCD﹣∠EDC=720°﹣240°=480°.
14.【解答】解:(1)∵所经过的路线正好构成一个外角是30度的正多边形,
∴360÷30=12,12×10=120(米);
答:小明一共走了120米;
(2)根据题意得:
(12﹣2)×180°=1800°,
答:这个多边形的内角和是1800°.
15.【解答】解:(1)如图,
∵∠1=∠C+∠E,∠2=∠B+∠D,
又∵∠A+∠1+∠2=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
故答案为:180°;
(2)①如图,∵∠QGF是△GBD的一个外角,
∴∠QGF=∠B+∠D.
同理,∠PFG=∠C+∠E.
∵在四边形PFGQ中,∠QGF+∠PFG+∠P+∠Q=(4﹣2)×180°=360°,
∴∠B+∠C+∠D+∠E+∠P+∠Q=360°.
②由(1)知,∠A+∠B+∠C+∠D+∠E=180°.
又∵∠B+∠C+∠D+∠E=8∠A,
∴∠A+8∠A=180°
∴∠A=20°.
∴∠B+∠C+∠D+∠E=160°.
由①知,∠B+∠C+∠D+∠E+∠P+∠Q=360°.
∴∠P+∠Q=360°﹣160°=200°.
一.选择题
1.若n边形的内角和等于它外角和的2倍,则边数n为( )
A.7 B.6 C.5 D.4
2.从n边形的一个顶点出发,可以作6条对角线,则n的值是( )
A.12 B.10 C.9 D.8
3.如图,顺次连接图中六个点,得到以下图形,则∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.270° C.360° D.720°
4.已知∠EOF=90°,现将一直角三角板ABC(∠A=30°、∠C=90°)按如图所示的位置摆放,则∠α+∠β=( )
A.210° B.200° C.190° D.180°
5.若一个多边形截去一个角后,变成五边形,则原来的多边形的边数可能为( )
A.5或6 B.4或5 C.3或4或5 D.4或5或6
二.填空题
6.如图,将五角星沿着虚线FG剪下.若∠B+∠C+∠D+∠E=5∠A,则∠CFG+∠DGF= .
7.一个多边形的每个内角均为108°,则这个多边形的边数为 .
8.如图,∠1=65°,∠2=85°,∠3=60°,∠4=40°,则∠5= .
9.如图,小明在操场上从A点出发,沿直线前进8米后向左转40°,再沿直线前进8米后,又向左转40°,这样走下去,他第一次回到出发地A点时,一共走了 米.
10.用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠CAE= °.
三.解答题
11.已知一个多边形的每一个内角都相等,并且每个内角都等于与它相邻的外角的3倍.
(1)这个多边形是几边形?
(2)求这个多边形的内角和.
12.如图,五边形ABCDE的内角都相等∠1=∠2,∠3=∠4.
(1)求∠E的度数.
(2)求x的值.
13.如图,在六边形ABCDEF中,∠BCD的平分线与∠CDE的平分线交于点P,∠P=60°.
(1)求六边形ABCDEF的内角和;
(2)求∠A+∠B+∠E+∠F的度数.
14.如图,小明从点A出发,前进10m后向右转30°,再前进10m后又向右转30°,……,如此反复下去,直到她第一次回到出发点A,他所走的路径构成了一个正多边形.
(1)求小明一共走了多少米;
(2)求这个正多边形的内角和.
15.例题再现:
(1)如图1,五角星的顶角分别是∠A,∠B,∠C,∠D,∠E,则∠A+∠B+∠C+∠D+∠E= (直接写出答案);
知识链接 n边形的内角和等于(n﹣2) 180°.
变式拓展:
(2)如图2,将该五角星剪掉一个顶角∠A.
①求∠B+∠C+∠D+∠E+∠P+∠Q的度数;
②若∠B+∠C+∠D+∠E=8∠A,求∠P+∠Q的度数.
参考答案
一、选择题
题号 1 2 3 4 5
答案 B C C A D
二、填空题
6.【解答】解:如图,∵∠AMN=∠C+∠E,∠ANM=∠B+∠D,而∠AMN+∠ANM+∠A=180°,
∴∠C+∠E+∠B+∠D=180°﹣∠A,
即∠A+∠B+∠C+∠D+∠E=180°,
又∵∠B+∠C+∠D+∠E=5∠A,
∴∠A+5∠A=180°,
解得∠A=30°,
∴∠CFG+∠DGF=∠AFG+∠AGF+∠A+∠A=180°+30°=210°,
故答案为:210°.
7.【解答】解:180°﹣108°=72°,
360°÷72°=5,
故答案为:5.
8.【解答】解:如图,连接BC,
在△BCE中,∠3+∠EBC+∠ECB=180°,
∵∠3=60°,
∴∠EBC+∠ECB=120°,
在四边形ABCD中,∠1+∠2+∠4+∠EBC+∠ECB+∠5=(4﹣2)×180°=360°,
∵∠1=65°,∠2=85°,∠4=40°,
∴65°+85°+40°+120°+∠5=360°,
∴∠5=50°,
故答案为:50°.
9.【解答】解:∵小明需要转360÷40=9次才会回到原点,
∴小明共走了9×8=72(米),
故答案为:72.
10.【解答】解:∵五边形ABCDE是正五边形,
∴∠ABC=∠BAE,AB=BC,
∴∠BAC=∠ACB,
∵∠ABC+∠BAC+∠ACB=180°,
∴∠BAC=∠ACB=36°,
∵∠BAE=∠BAC+∠CAE,
∴∠CAE=∠BAE﹣∠BAC=108°﹣36°=72°,
故答案为:72.
三、解答题
11.【解答】解:(1)设这个多边形的每个外角都为x°,则与它相邻的内角为3x°,由题意得:
x+3x=180,
4x=180,
x=45,
∴这个多边形的边数为:360÷45=8,
∴这个多边形是八边形;
(2)由(1)可知这个多边形是八边形,
∴这个多边形的内角和为:
(8﹣2)×180°=6×180°=1080°.
12.【解答】解:(1)由条件可知;
(2)由(1)可知∠CDE=∠E=108°,
∴,
同理∠3=36°,
∴∠ADB=∠CDE﹣∠1﹣∠3=108°﹣36°﹣36°=36°,
∴x=36.
13.【解答】解:(1)六边形ABCDEF的内角和=(6﹣2)×180°=720°;
(2)∵∠P=60°,
∴∠PCD+∠PDC=180°﹣∠P=180°﹣60°=120°,
∵PC平分∠BCD,PD平分∠EDC,
∴∠BCD+∠EDC=2∠PCD+2∠PDC=2×120°=240°,
∵∠A+∠B+∠E+∠F+∠BCD+∠EDC=720°,
∴∠A+∠B+∠E+∠F=720°﹣∠BCD﹣∠EDC=720°﹣240°=480°.
14.【解答】解:(1)∵所经过的路线正好构成一个外角是30度的正多边形,
∴360÷30=12,12×10=120(米);
答:小明一共走了120米;
(2)根据题意得:
(12﹣2)×180°=1800°,
答:这个多边形的内角和是1800°.
15.【解答】解:(1)如图,
∵∠1=∠C+∠E,∠2=∠B+∠D,
又∵∠A+∠1+∠2=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
故答案为:180°;
(2)①如图,∵∠QGF是△GBD的一个外角,
∴∠QGF=∠B+∠D.
同理,∠PFG=∠C+∠E.
∵在四边形PFGQ中,∠QGF+∠PFG+∠P+∠Q=(4﹣2)×180°=360°,
∴∠B+∠C+∠D+∠E+∠P+∠Q=360°.
②由(1)知,∠A+∠B+∠C+∠D+∠E=180°.
又∵∠B+∠C+∠D+∠E=8∠A,
∴∠A+8∠A=180°
∴∠A=20°.
∴∠B+∠C+∠D+∠E=160°.
由①知,∠B+∠C+∠D+∠E+∠P+∠Q=360°.
∴∠P+∠Q=360°﹣160°=200°.
