沪教版九年级数学下册 27.2圆心角、弧、弦、弦心距之间的关系 试题(含详解)
文档属性
| 名称 | 沪教版九年级数学下册 27.2圆心角、弧、弦、弦心距之间的关系 试题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 925.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 09:01:02 | ||
图片预览




文档简介
27.2圆心角、弧、弦、弦心距之间的关系
一、单选题
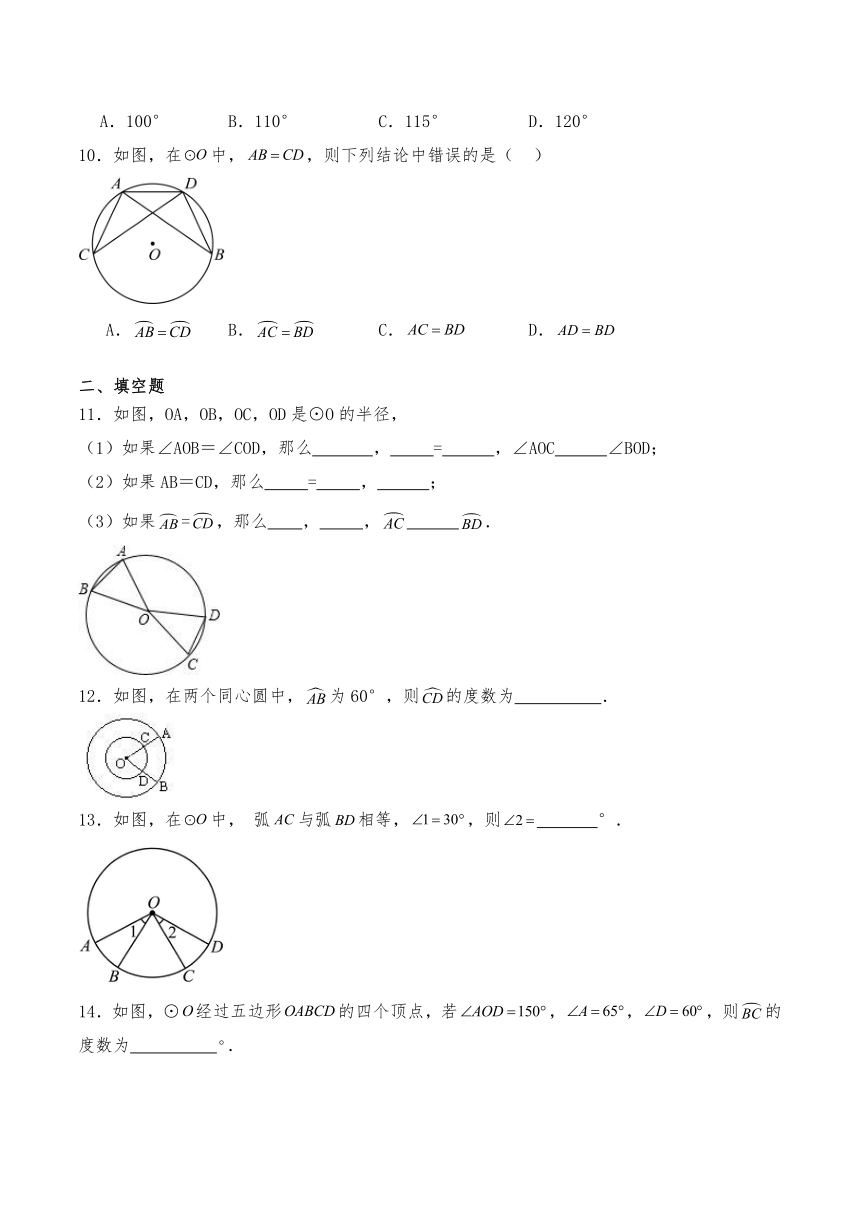
1.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
2.若C、D为半圆AB上三等分点,那么CD:AB为( )
A.2∶ B.1∶ C.2∶1 D.1∶2
3.下列说法中,不正确的是( )
A.在同圆或等圆中,若两弧相等,则它们所对的弦相等
B.在同一个圆中,若弦长等于半径,则该弦所对的劣弧的度数为60°
C.在同一个圆中,若两弧不等,则优弧所对的圆心角较大
D.若两弧的度数相等,则这两条弧是等弧
4.如图, AB是⊙O的直径, CD是AO的垂直平分线, EF是OB的垂直平分线, 则下列结论正确的是 ( )
A.== B.
C. D.
5.结合各自对应图形,给出的相应推理中,其中正确的是( )
∵ ∴= (1) ∵ ∴ (2) ∵ ∴ (3) ∵ ∴ (4)
A.(1)(2) B.(3)(4) C.(1)(3) D.(2)(4)
6.如图,扇形OAB的圆心角为90°,点C、D是的三等分点,半径OC、OD分别与弦AB交于点E、F,下列说法错误的是( )
A.AE=EF=FB B.AC=CD=DB
C.EC=FD D.∠DFB=75°
7.如图,是的两条互相垂直的弦,且,过点O作于点M,于点N.若,则的半径为( )
A. B.2 C. D.4
8.如图,AB是⊙O的直径,C、D是⊙O上的两点,且点C为弧BAD的中点,连接CD、CB、OD,CD与AB交于点F.若∠AOD=100°,则∠ABC的度数为( )
A.15° B.20° C.25° D.30°
9.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
10.如图,在中,,则下列结论中错误的是( )
A. B. C. D.
二、填空题
11.如图,OA,OB,OC,OD是⊙O的半径,
(1)如果∠AOB=∠COD,那么 , = ,∠AOC ∠BOD;
(2)如果AB=CD,那么 = , ;
(3)如果=,那么 , , .
12.如图,在两个同心圆中,为60°,则的度数为 .
13.如图,在中, 弧与弧相等,,则 °.
14.如图,⊙经过五边形的四个顶点,若,,,则的度数为 .
15.如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若,则∠P的大小为 度.
16.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
17.如图,D、E分别是⊙O的半径OA、OB上的点,CD⊥OA,CE⊥OB,CD= CE, 则弧AC与弧CB弧长的大小关系是 .
18.如图,扇形OAB中,∠AOB=60°,OA=4+8,点E为弧AB的中点,C为半径OA上一点,将线段CE绕点C逆时针旋转90°得到线段CE′,若点E′恰好落在半径OB上,则OE′= .
三、解答题
19.如图,在⊙O中,弦AB与弦CD相交于点M,且AB=CD,求证:BM=DM.
20.如图,在⊙O中,弦AD与BC交于点E,且AD=BC,连接AB、CD.
求证:(1)AB=CD;
(2)AE=CE.
21.已知:如图所示,AB,CD是的弦,OC,OD分别交AB于点E,F,且,求证:.
22.已知:如图,在⊙O中,弦AB与半径OE、OF交于点C、D,AC=BD,求证:
(1)OC=OD:
(2).
23.如图,MB,MD是⊙O的两条弦,点A,C分别在弧MB,弧MD上,且AB=CD,点M是弧AC的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于E,OE=1,⊙O的半径是2,求MD的长.
24.如图所示,以的顶点A为圆心,为半径作圆,分别交,于点E,F,延长交于G.
(1)求证:;
(2)若劣弧所对圆心角的度数为,求的度数.
25.如图,已知是的直径,点在上,且C是优弧的中点,过点C作于点D.
(1)求证:;
(2)连接,若,求的长.
26.如图,在扇形AOB中,,C、D是上两点,过点D作交OB于E点,在OD上取点F,使,连接CF并延长交OB于G点.
(1)求证:;
(2)若C、D是AB的三等分点,:
①求;
②请比较GE和BE的大小.
答案
一、单选题
1.B
【分析】根据圆心角,弦,弧之间的关系判断,注意条件.
【解析】A中,等弦所对应的弧可以相等也可以互补构成新圆;
B中,等弧所对应的弦相等,故选B
C中,圆心角相等所对应的弦可能互补;
D中,弦相等,圆心角可能互补;
故选B
2.D
【分析】根据圆心角定理可得∠AOC=∠COD=∠BOD=60°,则△OCD为等边三角形,即CD等于半径.
【解析】
∵C、D为半圆AB上三等分点,
∴∠AOC=∠COD=∠BOD=60°,
∴△OCD为等边三角形,
则CD=OC=AB.
故选D.
3.D
【分析】圆心角、弧、弦的关系是在同圆或等圆中发生的,因此在大小不等的两圆中,即使位于两圆中的两弧的度数相等,这两条弧也不是等弧,由此可知答案.
【解析】A. 在同圆或等圆中,若两弧相等,则它们所对的弦相等,此项说法正确,不符合题意;
B.在同一个圆中,若弦长等于半径,则该弦所对的劣弧的度数为60°,此项说法正确,不符合题意;
C. 在同一个圆中,若两弧不等,则优弧所对的圆心角较大,此项说法正确,不符合题意;
D.在大小不等的两圆中,即使位于两圆中的两弧的度数相等,这两条弧也不是等弧,符合题意.
故选:D.
4.A
【分析】如图,连接AD,OD,DF,OF,BF,根据垂直平分线的性质易证DF=DF=BF,再根据“在同圆或等圆中,所对的弦相等的两段弧是等弧”即可判断.
【解析】如图,连接AD,OD,DF,OF,BF,
∵CD是AO的垂直平分线, EF是OB的垂直平分线,
∴DF=CE=AB,AD=OD,OF=BF,
∴DF=DF=BF,
则==.
故选A.
5.C
【分析】根据弧、弦、圆心角的关系,即可判断.
【解析】(1)在⊙O中,∵,∴=,∴(1)正确;
(2)与不是同圆或等圆中的弧,由推不出,∴(2)不正确;
(3)∵,∴∴;∴(3)正确;
(4)弦与弦不是同圆或等圆中的弦,∴;(4)不正确
故选:C
6.A
【解析】试题分析:利用点C,D是的三等分点,得出AC=CD=DB,∠AOC=∠COD=∠BOD=∠AOB=30°,再求出∠OBA的度数,利用外角求出∠BFD的度数,通过证△AOE≌△BOF,得出OE=OF,则EC=FD.连接AC,在△ACE中,求证AE=AC,则可证CD=AE=BF,再根据CD>EF得AE、EF、FB 关系.
解:∵点C,D是的三等分点,
∴AC=CD=DB,∠AOC=∠COD=∠BOD=∠AOB=30°,
∴选项B正确;
∵OA=OB,∠AOB=90°,∴∠OAB=∠OBA=45°,
∴∠AEC=∠OAB+∠AOC=45°+30°=75°,同理∠DFB=75°,
故选项D正确.
∴∠AEO=∠BFO,
在△AOE和△BOF中,∠AEO=∠BFO,∠AOC=∠BOD,AO=BO,
∴△AOE≌△BOF,
∴OE=OF,
∴EC=FD,故选项C正确.
在△AOC中,∵OA=OC,∴∠ACO=∠CAO=(180°-30°)=75°,
∴∠ACO=∠AEC,
∴AC=AE,同理BF=BD,
又∵AC=CD=BD,
∴CD=AE=BF,
∵在△OCD中,OE=OF,OC=OD,
∴EF∴CD=AE=BF>EF,故A错误.
故选A.
7.C
【分析】利用垂径定理,弦、弦心距的关系求得,,证明四边形是正方形,利用勾股定理即可求解.
【解析】解:∵,,,
∴,,
∵,,,
∴四边形是矩形,
∵,
∴矩形是正方形,
连接,则.
故选:C.
8.B
【分析】先根据邻补角的性质求出∠BOD,再根据点C为弧BAD的中点,求出∠BOC的度数,再根据等腰三角形的性质即可求出∠ABC的度数.
【解析】∵∠AOD=100°,
∴∠BOD=180°-∠AOD=80°,
∵点C为弧BAD的中点
∴∠BOC=∠DOC=(360°-80°)=140°
∵OC=OB
∴∠ABC=∠BCO=(180°-140°)=20°
故选B.
9.C
【分析】过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,由于DE=FG=MN,所以弦的弦心距也相等,所以OB、OC是角平分线,根据∠A=50°,先求出,再求出,进而可求出∠BOC.
【解析】解:过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,
∵DE=FG=MN,
∴OP=OK=OQ,
∴OB、OC平分∠ABC和∠ACB,
,,
∵∠A=50°,
∴,
∴
,
∴∠BOC=
故选:C.
10.D
【分析】本题考查的是弧,弦,圆心角之间的关系,由逐一分析各选项即可得到答案.
【解析】解:∵,
∴,故A不符合题意;
∴,
∴,故B不符合题意;
∴,故C不符合题意;
∵不一定为的中点,
∴不一定成立,故D符合题意;
故选D
二、填空题
11. AB=CD, , , = , , ∠AOB=∠COD, AB=CD, ∠AOB=∠COD, =
【分析】根据在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等进行解答.
【解析】(1)∵∠AOB=∠COD,
∴AB=CD,=,∠AOC=∠BOD;
(2)∵AB=CD,
∴=,∠AOB=∠COD;
(3)∵=,
∴AB=CD,∠AOB=∠COD,=.
故答案为AB=CD,,,=,,,∠AOB=∠COD,AB=CD,∠AOB=∠COD,=
12.60°
【分析】根据圆心角定理可得∠AOB=60°,即∠COD=60°,则的度数为60°.
【解析】∵为60°,
∴∠AOB=60°,
∴∠COD=60°,
则的度数为60°.
故答案为60°.
13.30
【分析】由弧与弧相等推得弧和弧相等,再根据在同圆中,等弧所对的圆周角相等,从而求出的度数.
【解析】解:∵弧与弧相等,
∴弧和弧相等,
∴;
故答案为:30.
14.
【分析】利用等腰三角形的性质先求解,,再利用三角形的内角和定理可得,,再求解,从而可得答案.
【解析】解:∵,,
∴,,
∴,,
∴,
∴弧的度数为.
故答案为40.
15.60
【分析】连接OC、OD,根据圆心角、弧、弦的关系得到∠AOC=∠COD=∠DOB=60°,根据等边三角形的性质解答.
【解析】连接OC、OD,
∵,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC,OB=OD,
∴△AOC和△BOD都是等边三角形,
∴∠A=60°,∠B=60°,
∴∠P=60°,
故答案为60.
16.105°.
【分析】连接OD、OE,根据圆心角、弧、弦的关系定理求出∠AOD=35°,根据等腰三角形的性质和三角形内角和定理计算即可.
【解析】解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=180°-∠ODC-∠E=180°-35°-35°=110°,
∴∠AOE=∠DOE-∠AOD=110°-35°=75°,
∴∠BOE=180°-∠AOE=180°-75°=105°,
∴的度数是105°.
故答案为105°.
17.相等
【分析】根据直角三角形的判定定理HL,可得出△COD≌△COE,则∠COD=∠COE,再根据在同圆中,相等的圆心角所对的弧也相等得出结论.
【解析】∵CD⊥OA、CE⊥OB,
∴∠CDO=∠CEO=90 ,
∵CD=CE,CO=CO,
∴△COD≌△C0E,
∴∠COD=∠COE,
∴=.
故答案为相等.
18.
【分析】过点作于,过点作于,连接,如图,设,利用得到,,再利用点为弧的中点得到,所以,,接着证明△,则,,则可列方程,然后解方程求出,从而得到的长.
【解析】解:过点作于,过点作于,连接,如图,
设,
,
,,
点为弧的中点,
,
,
,
线段绕点逆时针旋转得到线段,
,,
,,
,
在和△中
,
△,
,,
,
,解得,
.
故答案为4.
三、解答题
19.证明:连接BD.
∵AB=CD
∴=
∴-=-,即=
∴∠D=∠B
∴BM=DM
20.证明:(1)∵AD=BC
∴=
∴-=-
即=
∴AB=CD
(2)连接AC
∵=
∴∠ACB=∠DAC
∴AE=CE
21.证明:如图,过点O作于点M.
,
.
同理,.
.
.
22.(1)证明:连接OA,OB,
∵OA=OB,
∴∠OAC=∠OBD.
在△OAC与△OBD中,
∵,
∴△OAC≌△OBD(SAS).
∴OC=OD.
(2)∵△OAC≌△OBD,
∴∠AOC=∠BOD,
∴.
23.证明:(1)∵AB=CD,
∴,
又∵点M是弧AC的中点,
∴,
∴,
即:,
∴MB=MD;
(2)过O作OE⊥MB于E,则ME=BE,连接OM,
在Rt△MOE中,OE=1,⊙O的半径OM=2,
∴ME===,
∴MD=MB=2ME=2.
24.(1)解:如图,连接,
为圆心,
,
,
四边形为平行四边形,
,
,,
,
;
(2)∵劣弧所对圆心角的度数为,
,
,
四边形为平行四边形,
,
.
25.(1)解:如图:连接,延长交于点H.
是优弧的中点,
,
,
,
直线垂直平分,
∴,,
∵,
∴,
,
.
(2)解:由(1)知,
∴,
.
设,则,
,
(舍去),
.
26.(1)解:∵DEOC,
∴∠COD=∠ODE,
∵OC=OD,OF=DE,
∴△OCF≌△DOE(SAS);
(2)解:①∵C、D是的三等分点,∠AOB=90°,
∴∠AOC=∠COD=∠BOD=30°,
∵△OCF≌△DOE,
∴∠OCF=∠DOE=30°,
∵∠COG=∠COD+∠DOB=60°,
∴∠OGC=90°.
②∵,
∴,
又∵∠DOE=30°,
∴OF=2,
∵∠OCF=∠COF=30°,
∴CF=OF,
∵△OCF≌△DOE,
∴OE=CF=OF=2,
∴,,
∵,
∴BE>GE.
一、单选题
1.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
2.若C、D为半圆AB上三等分点,那么CD:AB为( )
A.2∶ B.1∶ C.2∶1 D.1∶2
3.下列说法中,不正确的是( )
A.在同圆或等圆中,若两弧相等,则它们所对的弦相等
B.在同一个圆中,若弦长等于半径,则该弦所对的劣弧的度数为60°
C.在同一个圆中,若两弧不等,则优弧所对的圆心角较大
D.若两弧的度数相等,则这两条弧是等弧
4.如图, AB是⊙O的直径, CD是AO的垂直平分线, EF是OB的垂直平分线, 则下列结论正确的是 ( )
A.== B.
C. D.
5.结合各自对应图形,给出的相应推理中,其中正确的是( )
∵ ∴= (1) ∵ ∴ (2) ∵ ∴ (3) ∵ ∴ (4)
A.(1)(2) B.(3)(4) C.(1)(3) D.(2)(4)
6.如图,扇形OAB的圆心角为90°,点C、D是的三等分点,半径OC、OD分别与弦AB交于点E、F,下列说法错误的是( )
A.AE=EF=FB B.AC=CD=DB
C.EC=FD D.∠DFB=75°
7.如图,是的两条互相垂直的弦,且,过点O作于点M,于点N.若,则的半径为( )
A. B.2 C. D.4
8.如图,AB是⊙O的直径,C、D是⊙O上的两点,且点C为弧BAD的中点,连接CD、CB、OD,CD与AB交于点F.若∠AOD=100°,则∠ABC的度数为( )
A.15° B.20° C.25° D.30°
9.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
10.如图,在中,,则下列结论中错误的是( )
A. B. C. D.
二、填空题
11.如图,OA,OB,OC,OD是⊙O的半径,
(1)如果∠AOB=∠COD,那么 , = ,∠AOC ∠BOD;
(2)如果AB=CD,那么 = , ;
(3)如果=,那么 , , .
12.如图,在两个同心圆中,为60°,则的度数为 .
13.如图,在中, 弧与弧相等,,则 °.
14.如图,⊙经过五边形的四个顶点,若,,,则的度数为 .
15.如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若,则∠P的大小为 度.
16.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
17.如图,D、E分别是⊙O的半径OA、OB上的点,CD⊥OA,CE⊥OB,CD= CE, 则弧AC与弧CB弧长的大小关系是 .
18.如图,扇形OAB中,∠AOB=60°,OA=4+8,点E为弧AB的中点,C为半径OA上一点,将线段CE绕点C逆时针旋转90°得到线段CE′,若点E′恰好落在半径OB上,则OE′= .
三、解答题
19.如图,在⊙O中,弦AB与弦CD相交于点M,且AB=CD,求证:BM=DM.
20.如图,在⊙O中,弦AD与BC交于点E,且AD=BC,连接AB、CD.
求证:(1)AB=CD;
(2)AE=CE.
21.已知:如图所示,AB,CD是的弦,OC,OD分别交AB于点E,F,且,求证:.
22.已知:如图,在⊙O中,弦AB与半径OE、OF交于点C、D,AC=BD,求证:
(1)OC=OD:
(2).
23.如图,MB,MD是⊙O的两条弦,点A,C分别在弧MB,弧MD上,且AB=CD,点M是弧AC的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于E,OE=1,⊙O的半径是2,求MD的长.
24.如图所示,以的顶点A为圆心,为半径作圆,分别交,于点E,F,延长交于G.
(1)求证:;
(2)若劣弧所对圆心角的度数为,求的度数.
25.如图,已知是的直径,点在上,且C是优弧的中点,过点C作于点D.
(1)求证:;
(2)连接,若,求的长.
26.如图,在扇形AOB中,,C、D是上两点,过点D作交OB于E点,在OD上取点F,使,连接CF并延长交OB于G点.
(1)求证:;
(2)若C、D是AB的三等分点,:
①求;
②请比较GE和BE的大小.
答案
一、单选题
1.B
【分析】根据圆心角,弦,弧之间的关系判断,注意条件.
【解析】A中,等弦所对应的弧可以相等也可以互补构成新圆;
B中,等弧所对应的弦相等,故选B
C中,圆心角相等所对应的弦可能互补;
D中,弦相等,圆心角可能互补;
故选B
2.D
【分析】根据圆心角定理可得∠AOC=∠COD=∠BOD=60°,则△OCD为等边三角形,即CD等于半径.
【解析】
∵C、D为半圆AB上三等分点,
∴∠AOC=∠COD=∠BOD=60°,
∴△OCD为等边三角形,
则CD=OC=AB.
故选D.
3.D
【分析】圆心角、弧、弦的关系是在同圆或等圆中发生的,因此在大小不等的两圆中,即使位于两圆中的两弧的度数相等,这两条弧也不是等弧,由此可知答案.
【解析】A. 在同圆或等圆中,若两弧相等,则它们所对的弦相等,此项说法正确,不符合题意;
B.在同一个圆中,若弦长等于半径,则该弦所对的劣弧的度数为60°,此项说法正确,不符合题意;
C. 在同一个圆中,若两弧不等,则优弧所对的圆心角较大,此项说法正确,不符合题意;
D.在大小不等的两圆中,即使位于两圆中的两弧的度数相等,这两条弧也不是等弧,符合题意.
故选:D.
4.A
【分析】如图,连接AD,OD,DF,OF,BF,根据垂直平分线的性质易证DF=DF=BF,再根据“在同圆或等圆中,所对的弦相等的两段弧是等弧”即可判断.
【解析】如图,连接AD,OD,DF,OF,BF,
∵CD是AO的垂直平分线, EF是OB的垂直平分线,
∴DF=CE=AB,AD=OD,OF=BF,
∴DF=DF=BF,
则==.
故选A.
5.C
【分析】根据弧、弦、圆心角的关系,即可判断.
【解析】(1)在⊙O中,∵,∴=,∴(1)正确;
(2)与不是同圆或等圆中的弧,由推不出,∴(2)不正确;
(3)∵,∴∴;∴(3)正确;
(4)弦与弦不是同圆或等圆中的弦,∴;(4)不正确
故选:C
6.A
【解析】试题分析:利用点C,D是的三等分点,得出AC=CD=DB,∠AOC=∠COD=∠BOD=∠AOB=30°,再求出∠OBA的度数,利用外角求出∠BFD的度数,通过证△AOE≌△BOF,得出OE=OF,则EC=FD.连接AC,在△ACE中,求证AE=AC,则可证CD=AE=BF,再根据CD>EF得AE、EF、FB 关系.
解:∵点C,D是的三等分点,
∴AC=CD=DB,∠AOC=∠COD=∠BOD=∠AOB=30°,
∴选项B正确;
∵OA=OB,∠AOB=90°,∴∠OAB=∠OBA=45°,
∴∠AEC=∠OAB+∠AOC=45°+30°=75°,同理∠DFB=75°,
故选项D正确.
∴∠AEO=∠BFO,
在△AOE和△BOF中,∠AEO=∠BFO,∠AOC=∠BOD,AO=BO,
∴△AOE≌△BOF,
∴OE=OF,
∴EC=FD,故选项C正确.
在△AOC中,∵OA=OC,∴∠ACO=∠CAO=(180°-30°)=75°,
∴∠ACO=∠AEC,
∴AC=AE,同理BF=BD,
又∵AC=CD=BD,
∴CD=AE=BF,
∵在△OCD中,OE=OF,OC=OD,
∴EF
故选A.
7.C
【分析】利用垂径定理,弦、弦心距的关系求得,,证明四边形是正方形,利用勾股定理即可求解.
【解析】解:∵,,,
∴,,
∵,,,
∴四边形是矩形,
∵,
∴矩形是正方形,
连接,则.
故选:C.
8.B
【分析】先根据邻补角的性质求出∠BOD,再根据点C为弧BAD的中点,求出∠BOC的度数,再根据等腰三角形的性质即可求出∠ABC的度数.
【解析】∵∠AOD=100°,
∴∠BOD=180°-∠AOD=80°,
∵点C为弧BAD的中点
∴∠BOC=∠DOC=(360°-80°)=140°
∵OC=OB
∴∠ABC=∠BCO=(180°-140°)=20°
故选B.
9.C
【分析】过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,由于DE=FG=MN,所以弦的弦心距也相等,所以OB、OC是角平分线,根据∠A=50°,先求出,再求出,进而可求出∠BOC.
【解析】解:过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,
∵DE=FG=MN,
∴OP=OK=OQ,
∴OB、OC平分∠ABC和∠ACB,
,,
∵∠A=50°,
∴,
∴
,
∴∠BOC=
故选:C.
10.D
【分析】本题考查的是弧,弦,圆心角之间的关系,由逐一分析各选项即可得到答案.
【解析】解:∵,
∴,故A不符合题意;
∴,
∴,故B不符合题意;
∴,故C不符合题意;
∵不一定为的中点,
∴不一定成立,故D符合题意;
故选D
二、填空题
11. AB=CD, , , = , , ∠AOB=∠COD, AB=CD, ∠AOB=∠COD, =
【分析】根据在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等进行解答.
【解析】(1)∵∠AOB=∠COD,
∴AB=CD,=,∠AOC=∠BOD;
(2)∵AB=CD,
∴=,∠AOB=∠COD;
(3)∵=,
∴AB=CD,∠AOB=∠COD,=.
故答案为AB=CD,,,=,,,∠AOB=∠COD,AB=CD,∠AOB=∠COD,=
12.60°
【分析】根据圆心角定理可得∠AOB=60°,即∠COD=60°,则的度数为60°.
【解析】∵为60°,
∴∠AOB=60°,
∴∠COD=60°,
则的度数为60°.
故答案为60°.
13.30
【分析】由弧与弧相等推得弧和弧相等,再根据在同圆中,等弧所对的圆周角相等,从而求出的度数.
【解析】解:∵弧与弧相等,
∴弧和弧相等,
∴;
故答案为:30.
14.
【分析】利用等腰三角形的性质先求解,,再利用三角形的内角和定理可得,,再求解,从而可得答案.
【解析】解:∵,,
∴,,
∴,,
∴,
∴弧的度数为.
故答案为40.
15.60
【分析】连接OC、OD,根据圆心角、弧、弦的关系得到∠AOC=∠COD=∠DOB=60°,根据等边三角形的性质解答.
【解析】连接OC、OD,
∵,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC,OB=OD,
∴△AOC和△BOD都是等边三角形,
∴∠A=60°,∠B=60°,
∴∠P=60°,
故答案为60.
16.105°.
【分析】连接OD、OE,根据圆心角、弧、弦的关系定理求出∠AOD=35°,根据等腰三角形的性质和三角形内角和定理计算即可.
【解析】解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=180°-∠ODC-∠E=180°-35°-35°=110°,
∴∠AOE=∠DOE-∠AOD=110°-35°=75°,
∴∠BOE=180°-∠AOE=180°-75°=105°,
∴的度数是105°.
故答案为105°.
17.相等
【分析】根据直角三角形的判定定理HL,可得出△COD≌△COE,则∠COD=∠COE,再根据在同圆中,相等的圆心角所对的弧也相等得出结论.
【解析】∵CD⊥OA、CE⊥OB,
∴∠CDO=∠CEO=90 ,
∵CD=CE,CO=CO,
∴△COD≌△C0E,
∴∠COD=∠COE,
∴=.
故答案为相等.
18.
【分析】过点作于,过点作于,连接,如图,设,利用得到,,再利用点为弧的中点得到,所以,,接着证明△,则,,则可列方程,然后解方程求出,从而得到的长.
【解析】解:过点作于,过点作于,连接,如图,
设,
,
,,
点为弧的中点,
,
,
,
线段绕点逆时针旋转得到线段,
,,
,,
,
在和△中
,
△,
,,
,
,解得,
.
故答案为4.
三、解答题
19.证明:连接BD.
∵AB=CD
∴=
∴-=-,即=
∴∠D=∠B
∴BM=DM
20.证明:(1)∵AD=BC
∴=
∴-=-
即=
∴AB=CD
(2)连接AC
∵=
∴∠ACB=∠DAC
∴AE=CE
21.证明:如图,过点O作于点M.
,
.
同理,.
.
.
22.(1)证明:连接OA,OB,
∵OA=OB,
∴∠OAC=∠OBD.
在△OAC与△OBD中,
∵,
∴△OAC≌△OBD(SAS).
∴OC=OD.
(2)∵△OAC≌△OBD,
∴∠AOC=∠BOD,
∴.
23.证明:(1)∵AB=CD,
∴,
又∵点M是弧AC的中点,
∴,
∴,
即:,
∴MB=MD;
(2)过O作OE⊥MB于E,则ME=BE,连接OM,
在Rt△MOE中,OE=1,⊙O的半径OM=2,
∴ME===,
∴MD=MB=2ME=2.
24.(1)解:如图,连接,
为圆心,
,
,
四边形为平行四边形,
,
,,
,
;
(2)∵劣弧所对圆心角的度数为,
,
,
四边形为平行四边形,
,
.
25.(1)解:如图:连接,延长交于点H.
是优弧的中点,
,
,
,
直线垂直平分,
∴,,
∵,
∴,
,
.
(2)解:由(1)知,
∴,
.
设,则,
,
(舍去),
.
26.(1)解:∵DEOC,
∴∠COD=∠ODE,
∵OC=OD,OF=DE,
∴△OCF≌△DOE(SAS);
(2)解:①∵C、D是的三等分点,∠AOB=90°,
∴∠AOC=∠COD=∠BOD=30°,
∵△OCF≌△DOE,
∴∠OCF=∠DOE=30°,
∵∠COG=∠COD+∠DOB=60°,
∴∠OGC=90°.
②∵,
∴,
又∵∠DOE=30°,
∴OF=2,
∵∠OCF=∠COF=30°,
∴CF=OF,
∵△OCF≌△DOE,
∴OE=CF=OF=2,
∴,,
∵,
∴BE>GE.
