沪教版九年级数学下册 27.3垂径定理 试题(含详解)
文档属性
| 名称 | 沪教版九年级数学下册 27.3垂径定理 试题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 09:02:06 | ||
图片预览


文档简介
27.3垂径定理
一、单选题
1.如图,在中,于点C,若的半径为10,,则弦AB的长为( )
A. B. C. D.
2.下列命题中假命题是( )
A.平分弦的半径垂直于弦 B.垂直平分弦的直线必经过圆心
C.垂直于弦的直径平分这条弦所对的弧 D.平分弧的直径垂直平分这条弧所对的弦
3.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
4.已知⊙O的直径AB=10,弦CD⊥AB于点M,若OM:OA=3:5,则弦AC的长度( ).
A. B. C.3 D.或
5.如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3 B.4 C. D.
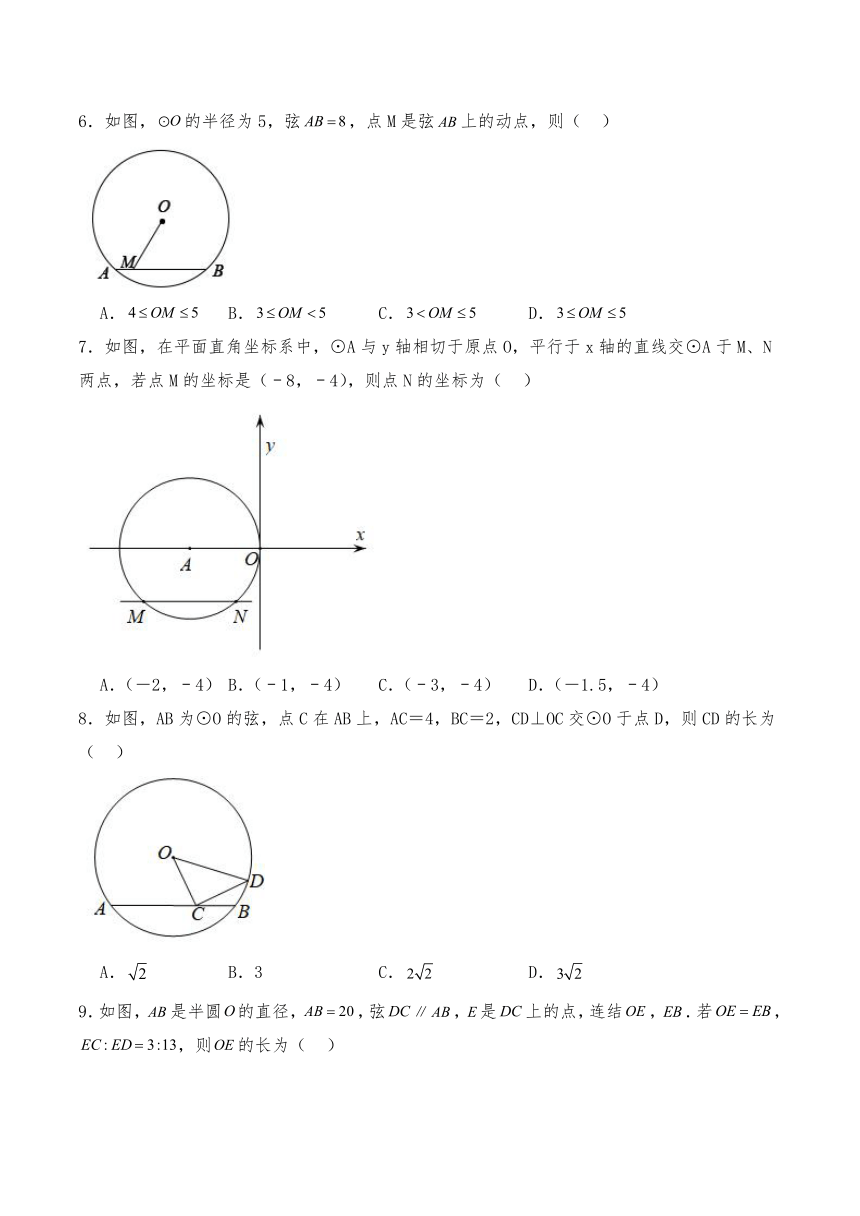
6.如图,的半径为5,弦,点M是弦上的动点,则( )
A. B. C. D.
7.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣8,﹣4),则点N的坐标为( )
A.(-2,﹣4) B.(﹣1,﹣4) C.(﹣3,﹣4) D.(-1.5,﹣4)
8.如图,AB为⊙O的弦,点C在AB上,AC=4,BC=2,CD⊥OC交⊙O于点D,则CD的长为( )
A. B.3 C. D.
9.如图,是半圆的直径,,弦,是上的点,连结,.若,,则的长为( )
A. B.8 C. D.
10.如图,是的弦(非直径),点是弦上的动点(不与点,重合),过点作垂直于的弦.若设的半径为,弦的长为,,则弦的长( )
A.与,,的值均有关 B.只与,的值有关
C.只与,的值有关 D.只与,的值有关
二、填空题
11.垂直于弦的直径 弦,并且 弦所对的两条弧.
符号语言:
∵①CD是直径,②CD⊥AB
∴③AE= ,④= ,⑤= .
12.如图,在中,于点的长为,则弦的长为 .
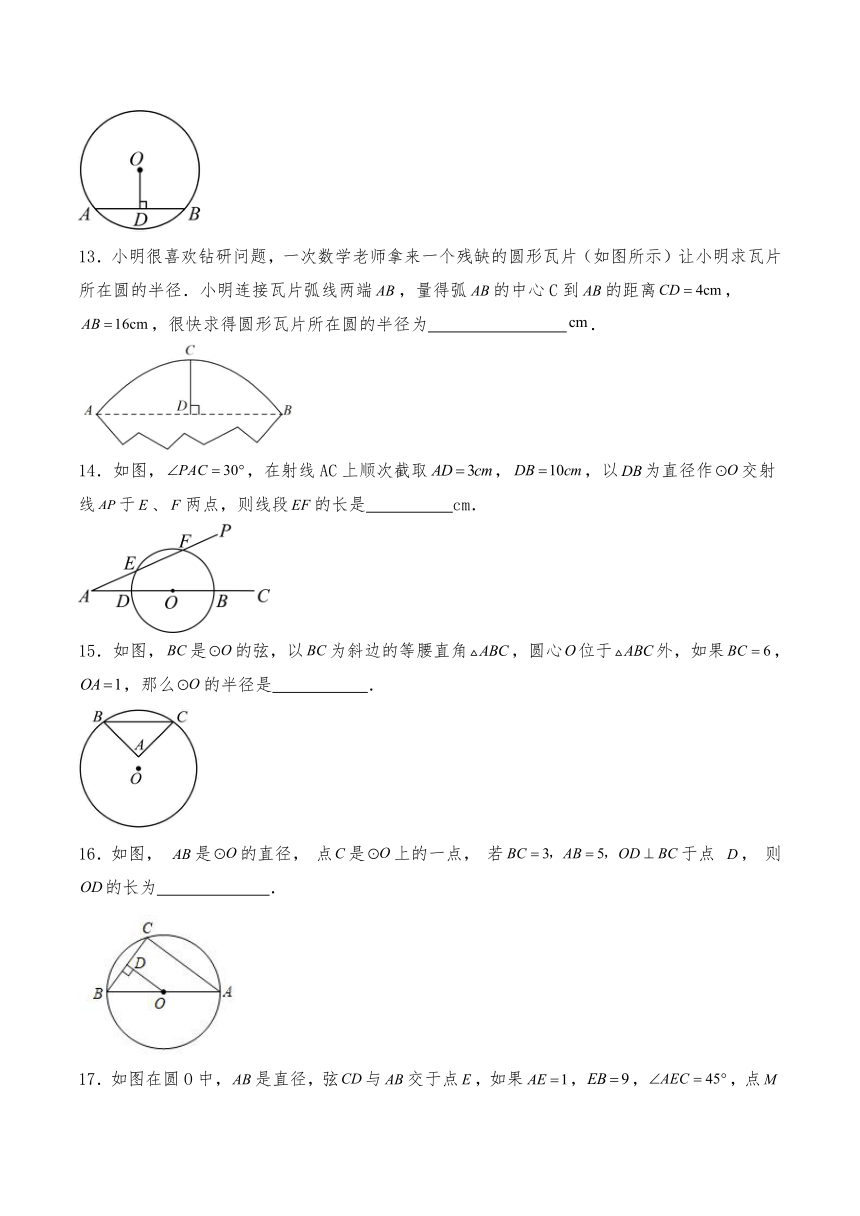
13.小明很喜欢钻研问题,一次数学老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径.小明连接瓦片弧线两端,量得弧的中心C到的距离,,很快求得圆形瓦片所在圆的半径为 .
14.如图,,在射线AC上顺次截取,,以为直径作交射线于、两点,则线段的长是 cm.
15.如图,是的弦,以为斜边的等腰直角,圆心位于外,如果,,那么的半径是 .
16.如图, 是的直径, 点是上的一点, 若于点 , 则的长为 .
17.如图在圆O中,是直径,弦与交于点,如果,,,点是的中点,连接,并延长与圆交于点,那么 .
18.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是 .
三、解答题
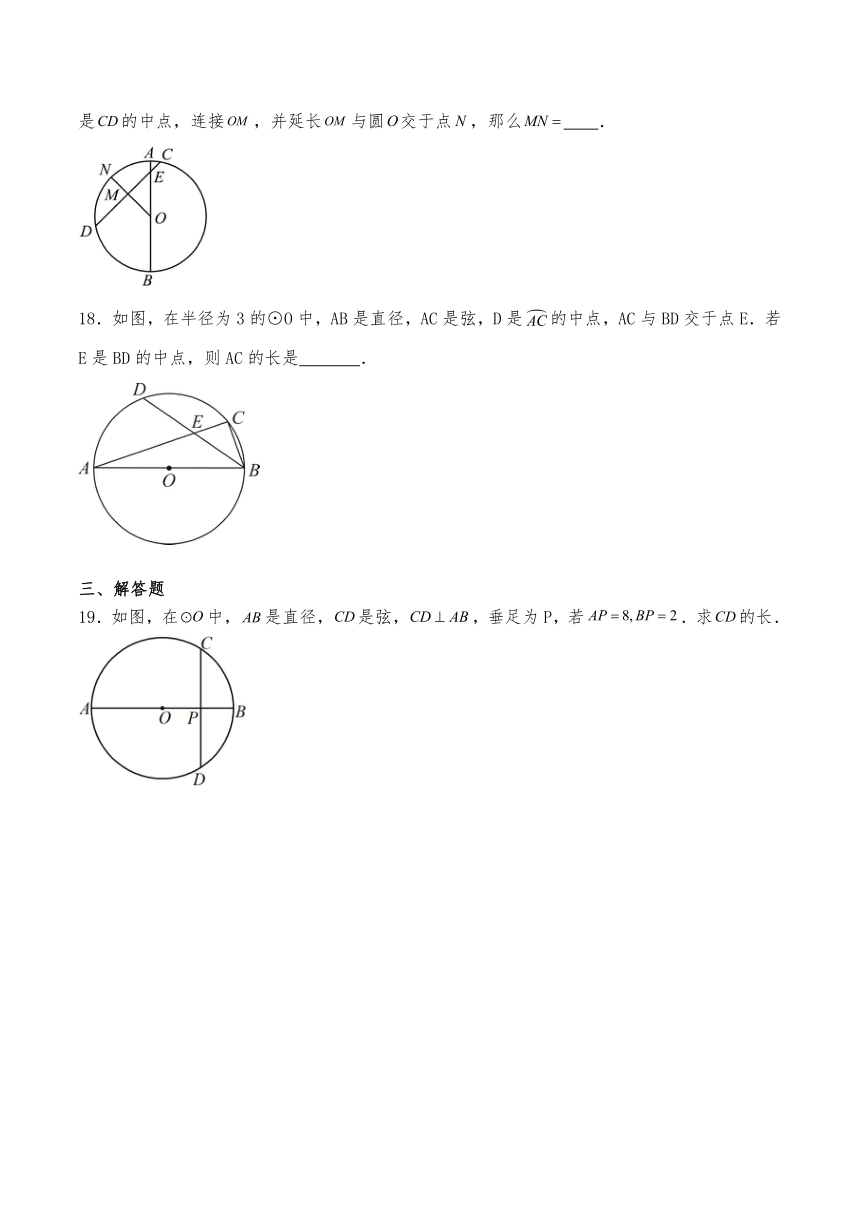
19.如图,在中,是直径,是弦,,垂足为P,若.求的长.
20.如图,已知为直径,是弦,且于点E,连接、.
(1)求证:;
(2)若,,求的半径.
21.如图,是的外接圆,平分的外角,,,垂足分别为点、,且.求证:
22.如图, 在中, , 以点为圆心, 长为半径作圆, 交于点 , 交于点, 连接.
(1)若, 求的度数;
(2)若, 求的长.
23.如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
(1)求线段OD的长;
(2)当时,求DE的长.
24.图1是某种型号圆形车载手机支架,由圆形钢轨、滑动杆、支撑杆组成.图2是它的正面示意图,滑动杆的两端都在圆O上,A、B两端可沿圆形钢轨滑动,支撑杆的底端C固定在圆O上,另一端D是滑动杆的中点,(即当支架水平放置时直线平行于水平线,支撑杆垂直于水平线),通过滑动A、B可以调节的高度.当经过圆心O时,它的宽度达到最大值,在支架水平放置的状态下:
(1)当滑动杆的宽度从10厘米向上升高调整到6厘米时,求此时支撑杆的高度.
(2)如图3,当某手机被支架锁住时,锁住高度与手机宽度恰好相等(),求该手机的宽度.
25.已知:如图,内接于,,点为弦的中点,的延长线交于点,联结,过点作交于点,联结.
(1)求证:;
(2)如果的半径为8,且,,求的长.
26.如图,在平面直角坐标系xOy中,半径为的与x轴交于、两点,且点C在x轴的上方.
(1)求圆心C的坐标;
(2)已知一个二次函数的图像经过点A、B、C,求这二次函数的解析式;
(3)设点P在y轴上,点M在(2)的二次函数图像上,如果以点P、M、A、B为顶点的四边形是平行四边形,请你直接写出点M的坐标.
答案
一、单选题
1.B
【分析】如图,连接,由垂径定理知垂直平分,则,在中,由勾股定理得求的值,根据求出的值即可.
【解析】解:如图,连接
由垂径定理知垂直平分
∴
在中,由勾股定理得
∴
故选B.
2.A
【分析】根据垂径定理及其推论分别进行判断.
【解析】A、平分弦(非直径)的半径垂直于弦,所以A为假命题;
B、垂直平分弦的直线必经过圆心,所以B选项为真命题;
C、垂直于弦的直径平分这条弦所对的弧,所以C选项为真命题;
D、平分弧的直径垂直平分这条弧所对的弦,所以D选项为真命题.
故选:A.
3.D
【解析】解:∵OC⊥AB,OC过圆心O点,
在中,由勾股定理得:
故选:D.
4.D
【分析】分两种情形:当点M在线段OA上或点M在线段AO的延长线上时,分别求解即可.
【解析】解:如图1,∵AB=10,弦CD⊥AB于点M.若OM:OA=3:5,
∴OA=OC=5,OM=3,AM=8,
∴CM==4,
∴AC==4;
如图2,∵AB=10cm,弦CD⊥AB于点M.若OM:OA=3:5,
∴OA=OC=5,OM=3,AM=2,
∴CM==4,
∴AC==2,
综上所述:弦AC的长为4或2.
故选:D.
5.C
【分析】作OM⊥AB于M,ON⊥CD于N,根据垂径定理、勾股定理得:OM=ON=4,再根据四边形MONP是正方形,故可求解.
【解析】作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
∵OB=5,BM= ,
∴OM=
∵AB=CD=8,
∴ON=OM=4,
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=3.
故选C.
6.D
【分析】过O作OM '⊥AB于M ',则OM '为OM 变化过程中的最小值,由垂径定理可求得M 'B,再由勾股定理可求得OM ',另可知OM变化过程中的最大值等于圆半径,如此问题可以得解.
【解析】解:如图,过O作OM '⊥AB于M ',则OM '为OM变化过程中的最小值,
由垂径定理可知M 'B=4,
∵OB=5,∴OM '=3,
又有OM变化过程中的最大值等于圆半径5,
∴3≤OM≤5,
故选D.
7.A
【分析】作AB⊥MN于B,连接AM,如图,设⊙A的半径为r,先根据切线的性质得OA=r,则点A的坐标为(-r,0),再利用垂径定理得BM=BN,利用MN∥x轴,M(-8,-4),得到B点坐标为(-r,-4),然后在Rt△ABM中,根据勾股定理得,解得r=5,则BM=BN=3,易得N点坐标为(-2,-4).
【解析】解:作AB⊥MN于B,连接AM,如图,
设⊙A的半径为r,
∵⊙A与y轴相切于原点O,
∴OA=r,
∴点A的坐标为(-r,0),
∵AB⊥MN,
∴BM=BN,
∵MN∥x轴,M(-8,-4),
∴B点坐标为(-r,-4),
在Rt△ABM中,AB=4,AM=r,BM=8-r,
∵,
∴,解得r=5,
∴BM=3,
∴BN=3,
∴N点坐标为(-2,-4),
故选:A.
8.C
【分析】过点O作OE⊥AB于点E,连接OA,OD,根据垂径定理可得AE=BE=3,从而得到CE=1,然后设OE=x,根据勾股定理可得,从而得到,即可求解.
【解析】解:如图,过点O作OE⊥AB于点E,连接OA,OD,
∴,
∵AC=4,BC=2,
∴BA=6,
∴AE=BE=3,
∴CE=1,
设OE=x,
∴,
∵CD⊥OC,
∴,
∴或(舍去).
故选:C
9.C
【分析】过点O作OM⊥CD,过点E作EN⊥AB,连接OC,设EC=3x,则ED=13x ,先证明四边形MONE是矩形,求出x的值,再根据勾股定理求出OM及OE的值.
【解析】解:过点O作OM⊥CD,过点E作EN⊥AB,连接OC,垂足分别为点M、N,
∵,
∴设EC=3x,则ED=13x ,
∴CD=16x,
∵OM⊥CD,
∴CM=DM=8x,
∴ME=CM-CE=8x-3x=5x,
∵OM⊥CD,,EN⊥AB,
∴∠MON=∠OME=∠ONE =90°,
∴四边形MONE是矩形,
∴ON=ME=5x,
∵AB=20,
∴OB=10,
∵,EN⊥AB,
∴ON=BN=5,
∴5x=5,即x=1,
∴CM=8,
∴,
∴
故选:C
10.D
【分析】连接AD、BE,先由垂径定理得,再根据得,用和表示出CE的长,即可得到DE的长.
【解析】解:如图,连接AD、BE,
∵DE为的弦,,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∵,
∴,,
∵,
∴,
∴,
故DE的长只与和的值有关.
故选:D.
二、填空题
11. 平分 平分 BE
【解析】略
12.
【分析】本题考查了垂径定理.根据垂径定理即可求解.
【解析】解:∵于点的长为,
∴.
故答案为:.
13.10
【分析】利用垂径定理和勾股定理进行求解即可.
【解析】解:设圆的半径为,
∵C为弧的中心,,
∴延长必过圆的圆心,设圆心为,连接,如图,
∴,
由勾股定理,得:,
即:,
解得:;
∴圆形瓦片所在圆的半径为:;
故答案为:10.
14.6
【分析】过点作于,连,根据垂径定理得,在中,,,利用含30度的直角三角形三边的关系可得到,再利用勾股定理计算出,由得到答案.
【解析】解:过点作于,连,如图
则,
在中,,,
则,
在中,,,
则,
则.
故答案为6.
15.5
【分析】此题主要考查了等腰直角三角形以及勾股定理等知识,正确应用勾股定理是解题关键.根据题意得出,,进而利用勾股定理得出答案.
【解析】解:连接并延长交于点,连接,,
,,
是的垂直平分线,
,,
是等腰直角形,,,
,,,
.
故答案为:5.
16.2
【分析】根据题意易得,则根据勾股定理可求解.
【解析】解:∵是的直径,
∴,
∵,
∴,
∵,
∴在中,由勾股定理得:;
故答案为2.
17.
【分析】此题考查了垂径定理、勾股定理,熟记垂径定理、勾股定理是解题的关键.
连接,,根据点是的中点,证,得为直角三角形,根据已知条件求出半径,进而求得,根据,利用勾股定理求出,即可得到。
【解析】
点是的中点,
,
在和中,
,
,
,
,,是直径,
,
,
在中,,
,
,
,
,
故答案为:.
18.
【分析】连接OD,交AC于F,根据垂径定理的推论得出OD⊥AC,AF=CF,进而证得DF=BC,根据三角形中位线定理求得OF=BC=DF,从而求得BC=DF,利用勾股定理即可求得AC.
【解析】解:如图,连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中,
,
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,AB=2OD=6,
∴BC=2,
∴.
故答案为:.
三、解答题
19.解:连接,
∵,
∴,
∴,
∴,
∵,
∴,
在中,
∵,
∴,
∴.
20.(1)∵为直径,是弦,且于点E,
∴,
∴;
(2)连接,如图,
设的半径为R,则,
又,
在中,由勾股定理可得
,即 ,
解得,
∴
21.解:∵,
∴,
∵平分,
∴,
∴,
∴,
∵,,
∴,
∴,
在和中,
,
∴,
∴.
22.(1)解:如图,连接.
,,
.
,
,
,
.
又,
.
(2)解:如图,过点作,垂足为.
,,,
.
又,
,
.
,,
.
23.(1)解:连接OB.
∵过圆心,且D是弦中点,
∴,
在中,.
∵.
∴;
(2)解:在中,.
设,则,
∴,
解得(舍),.
则.
24.(1)解:如图,连结OA,由题意可得:的直径为10,
∴OA=5,
∵CD⊥AB 即
∵OD==4,
∴CD=OC+OD=9.
所以此时支撑杆的高度为9cm.
(2)解:如图,记圆心为O,连结OA,
由题意可得:
∴四边形为正方形,
∵CD⊥EF
∴AE=CD=BF=AB,
∵CD⊥AB
设
则
∵OA=OC=5,
∴OD=2x-5
由勾股定理可得:
解得
经检验不符合题意,舍去,取
(cm),
即手机的宽度为8cm.
25.(1)证明:如图1所示:
,,
直线AD经过圆心O,
,,
点E为弦AB的中点,
是的中位线.
,
,
,
,
.
,
,
,
又,
,
;
(2)证明:联结如图所示:
,,
是等腰直角三角形,
.
,
,且,
.
∴∠BFC= =45°,
,
和△CFG均为等腰直角三角形,
AB.CG=FG=FC;
∵AC=AB=BF=12
∴AG=BG=6,CG=FG=12-6
∴CF=(12-6)×=12-12
26.(1)连接AC,过点C作CH⊥AB,垂直为H,
由垂径定理得:AH=AB=2,
则OH=1,
由勾股定理得:CH=4.
又点C在x轴的上方,
∴点C的坐标为(1,4).
(2)设二次函数的解析式为y=ax2+bx+c,
由题意,得,解这个方程组,得,
∴这二次函数的解析式为y=-x2+2x+3.
(3)①当四边形APBM是平行四边形时,过点M作MK⊥x轴,
∴PA=BM,∠AOP=∠BKM=90°,∠OAP=∠KBM,
∴△AOP≌△BKM,则BK=OA=1,则点M的横坐标为2,
∴y=-4+4+3=3,
∴此时点M的坐标为(2,3);
②∵当PM∥AB,PM=AB时,四边形APMB是平行四边形,
则设M的坐标为(4,y),则可得y=-16+8+3=-5,
则此时点M的坐标为(4,-5);
③当四边形ABPM是平行四边形时,
设点M的坐标为(-4,y),
则可得y=-16-8+3=-21,
则此时点M的坐标为(-4,-21).
∴点M的坐标为(2,3)或(4,-5)或(-4,-21).
一、单选题
1.如图,在中,于点C,若的半径为10,,则弦AB的长为( )
A. B. C. D.
2.下列命题中假命题是( )
A.平分弦的半径垂直于弦 B.垂直平分弦的直线必经过圆心
C.垂直于弦的直径平分这条弦所对的弧 D.平分弧的直径垂直平分这条弧所对的弦
3.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
4.已知⊙O的直径AB=10,弦CD⊥AB于点M,若OM:OA=3:5,则弦AC的长度( ).
A. B. C.3 D.或
5.如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3 B.4 C. D.
6.如图,的半径为5,弦,点M是弦上的动点,则( )
A. B. C. D.
7.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣8,﹣4),则点N的坐标为( )
A.(-2,﹣4) B.(﹣1,﹣4) C.(﹣3,﹣4) D.(-1.5,﹣4)
8.如图,AB为⊙O的弦,点C在AB上,AC=4,BC=2,CD⊥OC交⊙O于点D,则CD的长为( )
A. B.3 C. D.
9.如图,是半圆的直径,,弦,是上的点,连结,.若,,则的长为( )
A. B.8 C. D.
10.如图,是的弦(非直径),点是弦上的动点(不与点,重合),过点作垂直于的弦.若设的半径为,弦的长为,,则弦的长( )
A.与,,的值均有关 B.只与,的值有关
C.只与,的值有关 D.只与,的值有关
二、填空题
11.垂直于弦的直径 弦,并且 弦所对的两条弧.
符号语言:
∵①CD是直径,②CD⊥AB
∴③AE= ,④= ,⑤= .
12.如图,在中,于点的长为,则弦的长为 .
13.小明很喜欢钻研问题,一次数学老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径.小明连接瓦片弧线两端,量得弧的中心C到的距离,,很快求得圆形瓦片所在圆的半径为 .
14.如图,,在射线AC上顺次截取,,以为直径作交射线于、两点,则线段的长是 cm.
15.如图,是的弦,以为斜边的等腰直角,圆心位于外,如果,,那么的半径是 .
16.如图, 是的直径, 点是上的一点, 若于点 , 则的长为 .
17.如图在圆O中,是直径,弦与交于点,如果,,,点是的中点,连接,并延长与圆交于点,那么 .
18.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是 .
三、解答题
19.如图,在中,是直径,是弦,,垂足为P,若.求的长.
20.如图,已知为直径,是弦,且于点E,连接、.
(1)求证:;
(2)若,,求的半径.
21.如图,是的外接圆,平分的外角,,,垂足分别为点、,且.求证:
22.如图, 在中, , 以点为圆心, 长为半径作圆, 交于点 , 交于点, 连接.
(1)若, 求的度数;
(2)若, 求的长.
23.如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
(1)求线段OD的长;
(2)当时,求DE的长.
24.图1是某种型号圆形车载手机支架,由圆形钢轨、滑动杆、支撑杆组成.图2是它的正面示意图,滑动杆的两端都在圆O上,A、B两端可沿圆形钢轨滑动,支撑杆的底端C固定在圆O上,另一端D是滑动杆的中点,(即当支架水平放置时直线平行于水平线,支撑杆垂直于水平线),通过滑动A、B可以调节的高度.当经过圆心O时,它的宽度达到最大值,在支架水平放置的状态下:
(1)当滑动杆的宽度从10厘米向上升高调整到6厘米时,求此时支撑杆的高度.
(2)如图3,当某手机被支架锁住时,锁住高度与手机宽度恰好相等(),求该手机的宽度.
25.已知:如图,内接于,,点为弦的中点,的延长线交于点,联结,过点作交于点,联结.
(1)求证:;
(2)如果的半径为8,且,,求的长.
26.如图,在平面直角坐标系xOy中,半径为的与x轴交于、两点,且点C在x轴的上方.
(1)求圆心C的坐标;
(2)已知一个二次函数的图像经过点A、B、C,求这二次函数的解析式;
(3)设点P在y轴上,点M在(2)的二次函数图像上,如果以点P、M、A、B为顶点的四边形是平行四边形,请你直接写出点M的坐标.
答案
一、单选题
1.B
【分析】如图,连接,由垂径定理知垂直平分,则,在中,由勾股定理得求的值,根据求出的值即可.
【解析】解:如图,连接
由垂径定理知垂直平分
∴
在中,由勾股定理得
∴
故选B.
2.A
【分析】根据垂径定理及其推论分别进行判断.
【解析】A、平分弦(非直径)的半径垂直于弦,所以A为假命题;
B、垂直平分弦的直线必经过圆心,所以B选项为真命题;
C、垂直于弦的直径平分这条弦所对的弧,所以C选项为真命题;
D、平分弧的直径垂直平分这条弧所对的弦,所以D选项为真命题.
故选:A.
3.D
【解析】解:∵OC⊥AB,OC过圆心O点,
在中,由勾股定理得:
故选:D.
4.D
【分析】分两种情形:当点M在线段OA上或点M在线段AO的延长线上时,分别求解即可.
【解析】解:如图1,∵AB=10,弦CD⊥AB于点M.若OM:OA=3:5,
∴OA=OC=5,OM=3,AM=8,
∴CM==4,
∴AC==4;
如图2,∵AB=10cm,弦CD⊥AB于点M.若OM:OA=3:5,
∴OA=OC=5,OM=3,AM=2,
∴CM==4,
∴AC==2,
综上所述:弦AC的长为4或2.
故选:D.
5.C
【分析】作OM⊥AB于M,ON⊥CD于N,根据垂径定理、勾股定理得:OM=ON=4,再根据四边形MONP是正方形,故可求解.
【解析】作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
∵OB=5,BM= ,
∴OM=
∵AB=CD=8,
∴ON=OM=4,
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=3.
故选C.
6.D
【分析】过O作OM '⊥AB于M ',则OM '为OM 变化过程中的最小值,由垂径定理可求得M 'B,再由勾股定理可求得OM ',另可知OM变化过程中的最大值等于圆半径,如此问题可以得解.
【解析】解:如图,过O作OM '⊥AB于M ',则OM '为OM变化过程中的最小值,
由垂径定理可知M 'B=4,
∵OB=5,∴OM '=3,
又有OM变化过程中的最大值等于圆半径5,
∴3≤OM≤5,
故选D.
7.A
【分析】作AB⊥MN于B,连接AM,如图,设⊙A的半径为r,先根据切线的性质得OA=r,则点A的坐标为(-r,0),再利用垂径定理得BM=BN,利用MN∥x轴,M(-8,-4),得到B点坐标为(-r,-4),然后在Rt△ABM中,根据勾股定理得,解得r=5,则BM=BN=3,易得N点坐标为(-2,-4).
【解析】解:作AB⊥MN于B,连接AM,如图,
设⊙A的半径为r,
∵⊙A与y轴相切于原点O,
∴OA=r,
∴点A的坐标为(-r,0),
∵AB⊥MN,
∴BM=BN,
∵MN∥x轴,M(-8,-4),
∴B点坐标为(-r,-4),
在Rt△ABM中,AB=4,AM=r,BM=8-r,
∵,
∴,解得r=5,
∴BM=3,
∴BN=3,
∴N点坐标为(-2,-4),
故选:A.
8.C
【分析】过点O作OE⊥AB于点E,连接OA,OD,根据垂径定理可得AE=BE=3,从而得到CE=1,然后设OE=x,根据勾股定理可得,从而得到,即可求解.
【解析】解:如图,过点O作OE⊥AB于点E,连接OA,OD,
∴,
∵AC=4,BC=2,
∴BA=6,
∴AE=BE=3,
∴CE=1,
设OE=x,
∴,
∵CD⊥OC,
∴,
∴或(舍去).
故选:C
9.C
【分析】过点O作OM⊥CD,过点E作EN⊥AB,连接OC,设EC=3x,则ED=13x ,先证明四边形MONE是矩形,求出x的值,再根据勾股定理求出OM及OE的值.
【解析】解:过点O作OM⊥CD,过点E作EN⊥AB,连接OC,垂足分别为点M、N,
∵,
∴设EC=3x,则ED=13x ,
∴CD=16x,
∵OM⊥CD,
∴CM=DM=8x,
∴ME=CM-CE=8x-3x=5x,
∵OM⊥CD,,EN⊥AB,
∴∠MON=∠OME=∠ONE =90°,
∴四边形MONE是矩形,
∴ON=ME=5x,
∵AB=20,
∴OB=10,
∵,EN⊥AB,
∴ON=BN=5,
∴5x=5,即x=1,
∴CM=8,
∴,
∴
故选:C
10.D
【分析】连接AD、BE,先由垂径定理得,再根据得,用和表示出CE的长,即可得到DE的长.
【解析】解:如图,连接AD、BE,
∵DE为的弦,,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∵,
∴,,
∵,
∴,
∴,
故DE的长只与和的值有关.
故选:D.
二、填空题
11. 平分 平分 BE
【解析】略
12.
【分析】本题考查了垂径定理.根据垂径定理即可求解.
【解析】解:∵于点的长为,
∴.
故答案为:.
13.10
【分析】利用垂径定理和勾股定理进行求解即可.
【解析】解:设圆的半径为,
∵C为弧的中心,,
∴延长必过圆的圆心,设圆心为,连接,如图,
∴,
由勾股定理,得:,
即:,
解得:;
∴圆形瓦片所在圆的半径为:;
故答案为:10.
14.6
【分析】过点作于,连,根据垂径定理得,在中,,,利用含30度的直角三角形三边的关系可得到,再利用勾股定理计算出,由得到答案.
【解析】解:过点作于,连,如图
则,
在中,,,
则,
在中,,,
则,
则.
故答案为6.
15.5
【分析】此题主要考查了等腰直角三角形以及勾股定理等知识,正确应用勾股定理是解题关键.根据题意得出,,进而利用勾股定理得出答案.
【解析】解:连接并延长交于点,连接,,
,,
是的垂直平分线,
,,
是等腰直角形,,,
,,,
.
故答案为:5.
16.2
【分析】根据题意易得,则根据勾股定理可求解.
【解析】解:∵是的直径,
∴,
∵,
∴,
∵,
∴在中,由勾股定理得:;
故答案为2.
17.
【分析】此题考查了垂径定理、勾股定理,熟记垂径定理、勾股定理是解题的关键.
连接,,根据点是的中点,证,得为直角三角形,根据已知条件求出半径,进而求得,根据,利用勾股定理求出,即可得到。
【解析】
点是的中点,
,
在和中,
,
,
,
,,是直径,
,
,
在中,,
,
,
,
,
故答案为:.
18.
【分析】连接OD,交AC于F,根据垂径定理的推论得出OD⊥AC,AF=CF,进而证得DF=BC,根据三角形中位线定理求得OF=BC=DF,从而求得BC=DF,利用勾股定理即可求得AC.
【解析】解:如图,连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中,
,
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,AB=2OD=6,
∴BC=2,
∴.
故答案为:.
三、解答题
19.解:连接,
∵,
∴,
∴,
∴,
∵,
∴,
在中,
∵,
∴,
∴.
20.(1)∵为直径,是弦,且于点E,
∴,
∴;
(2)连接,如图,
设的半径为R,则,
又,
在中,由勾股定理可得
,即 ,
解得,
∴
21.解:∵,
∴,
∵平分,
∴,
∴,
∴,
∵,,
∴,
∴,
在和中,
,
∴,
∴.
22.(1)解:如图,连接.
,,
.
,
,
,
.
又,
.
(2)解:如图,过点作,垂足为.
,,,
.
又,
,
.
,,
.
23.(1)解:连接OB.
∵过圆心,且D是弦中点,
∴,
在中,.
∵.
∴;
(2)解:在中,.
设,则,
∴,
解得(舍),.
则.
24.(1)解:如图,连结OA,由题意可得:的直径为10,
∴OA=5,
∵CD⊥AB 即
∵OD==4,
∴CD=OC+OD=9.
所以此时支撑杆的高度为9cm.
(2)解:如图,记圆心为O,连结OA,
由题意可得:
∴四边形为正方形,
∵CD⊥EF
∴AE=CD=BF=AB,
∵CD⊥AB
设
则
∵OA=OC=5,
∴OD=2x-5
由勾股定理可得:
解得
经检验不符合题意,舍去,取
(cm),
即手机的宽度为8cm.
25.(1)证明:如图1所示:
,,
直线AD经过圆心O,
,,
点E为弦AB的中点,
是的中位线.
,
,
,
,
.
,
,
,
又,
,
;
(2)证明:联结如图所示:
,,
是等腰直角三角形,
.
,
,且,
.
∴∠BFC= =45°,
,
和△CFG均为等腰直角三角形,
AB.CG=FG=FC;
∵AC=AB=BF=12
∴AG=BG=6,CG=FG=12-6
∴CF=(12-6)×=12-12
26.(1)连接AC,过点C作CH⊥AB,垂直为H,
由垂径定理得:AH=AB=2,
则OH=1,
由勾股定理得:CH=4.
又点C在x轴的上方,
∴点C的坐标为(1,4).
(2)设二次函数的解析式为y=ax2+bx+c,
由题意,得,解这个方程组,得,
∴这二次函数的解析式为y=-x2+2x+3.
(3)①当四边形APBM是平行四边形时,过点M作MK⊥x轴,
∴PA=BM,∠AOP=∠BKM=90°,∠OAP=∠KBM,
∴△AOP≌△BKM,则BK=OA=1,则点M的横坐标为2,
∴y=-4+4+3=3,
∴此时点M的坐标为(2,3);
②∵当PM∥AB,PM=AB时,四边形APMB是平行四边形,
则设M的坐标为(4,y),则可得y=-16+8+3=-5,
则此时点M的坐标为(4,-5);
③当四边形ABPM是平行四边形时,
设点M的坐标为(-4,y),
则可得y=-16-8+3=-21,
则此时点M的坐标为(-4,-21).
∴点M的坐标为(2,3)或(4,-5)或(-4,-21).
