沪教版九年级数学下册 27.6正多边形与圆 试题(含详解)
文档属性
| 名称 | 沪教版九年级数学下册 27.6正多边形与圆 试题(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 1016.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 00:00:00 | ||
图片预览


文档简介
27.6正多边形与圆
一、单选题
1.如果一个正多边形的中心角等于,那么这个多边形的内角和为( )
A. B. C. D.
2.已知正六边形的边心距为,则它的半径为( )
A.2 B.4 C.2 D.4
3.下列正多边形中,中心角等于内角的是( )
A.正六边形 B.正五边形 C.正四边形 D.正三边形
4.如果正十边形的边长为a,那么它的半径是( )
A. B. C. D.
5.如果某正多边形的外接圆半径是其内切圆半径的倍,那么这个正多边形的边数是( )
A.3 B.4 C.5 D.无法确定
6.若一个正n边形(n为大于2的整数)的半径为r,则这个正n变形的边心距为( )
A. B. C. D.
7.如果一个正多边形的中心角为,那么这个正多边形的边数是( ).
A. B. C. D.
8.⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则n的值为( )
A.3 B.4 C.6 D.8
9.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
A.2, B.2 ,π C., D.2,
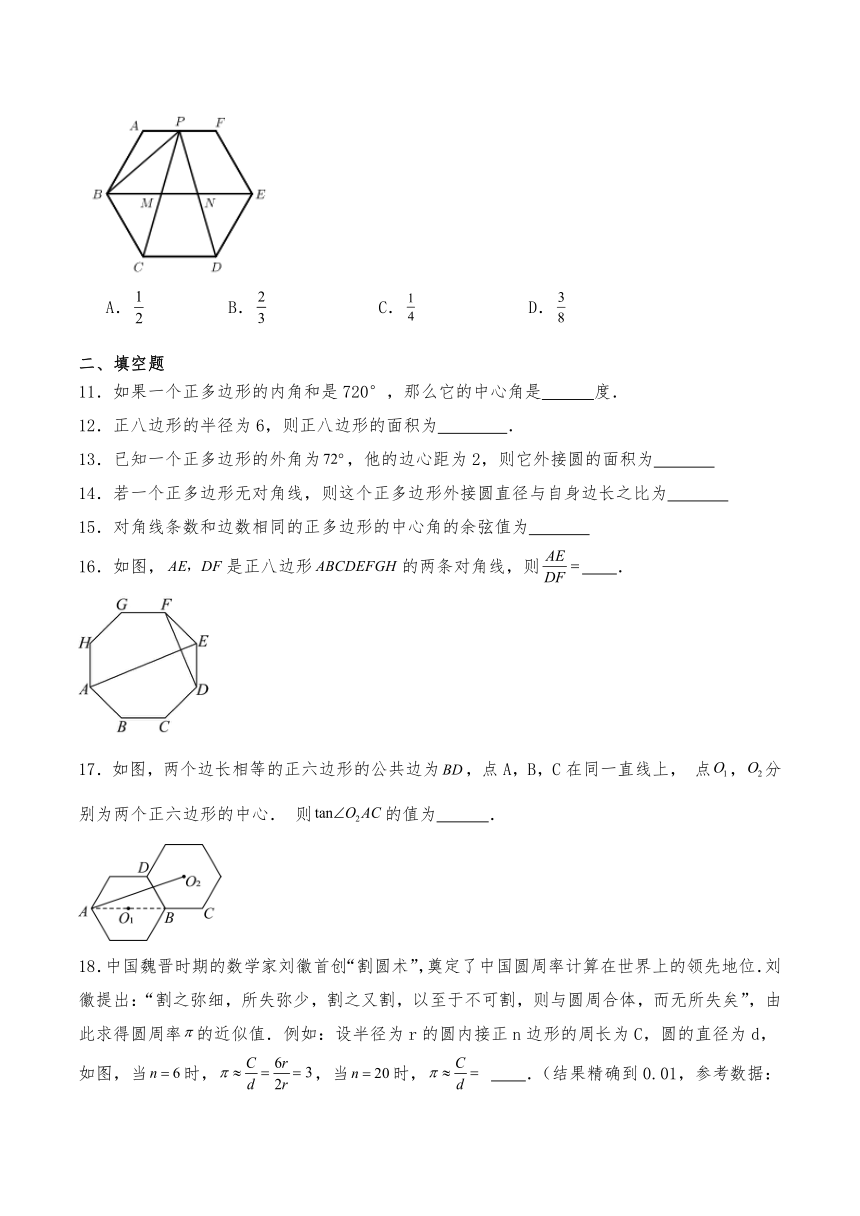
10.如图,六边形是正六边形,点是边的中点,,分别与交于点,,则的值为( ).
A. B. C. D.
二、填空题
11.如果一个正多边形的内角和是720°,那么它的中心角是 度.
12.正八边形的半径为6,则正八边形的面积为 .
13.已知一个正多边形的外角为,他的边心距为2,则它外接圆的面积为
14.若一个正多边形无对角线,则这个正多边形外接圆直径与自身边长之比为
15.对角线条数和边数相同的正多边形的中心角的余弦值为
16.如图,是正八边形的两条对角线,则 .
17.如图,两个边长相等的正六边形的公共边为,点A,B,C在同一直线上, 点,分别为两个正六边形的中心. 则的值为 .
18.中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,由此求得圆周率的近似值.例如:设半径为r的圆内接正n边形的周长为C,圆的直径为d,如图,当时,,当时, .(结果精确到0.01,参考数据:,)
三、解答题
19.如图,等边三角形 的边长为 ,求它的中心角、半径和边心距.
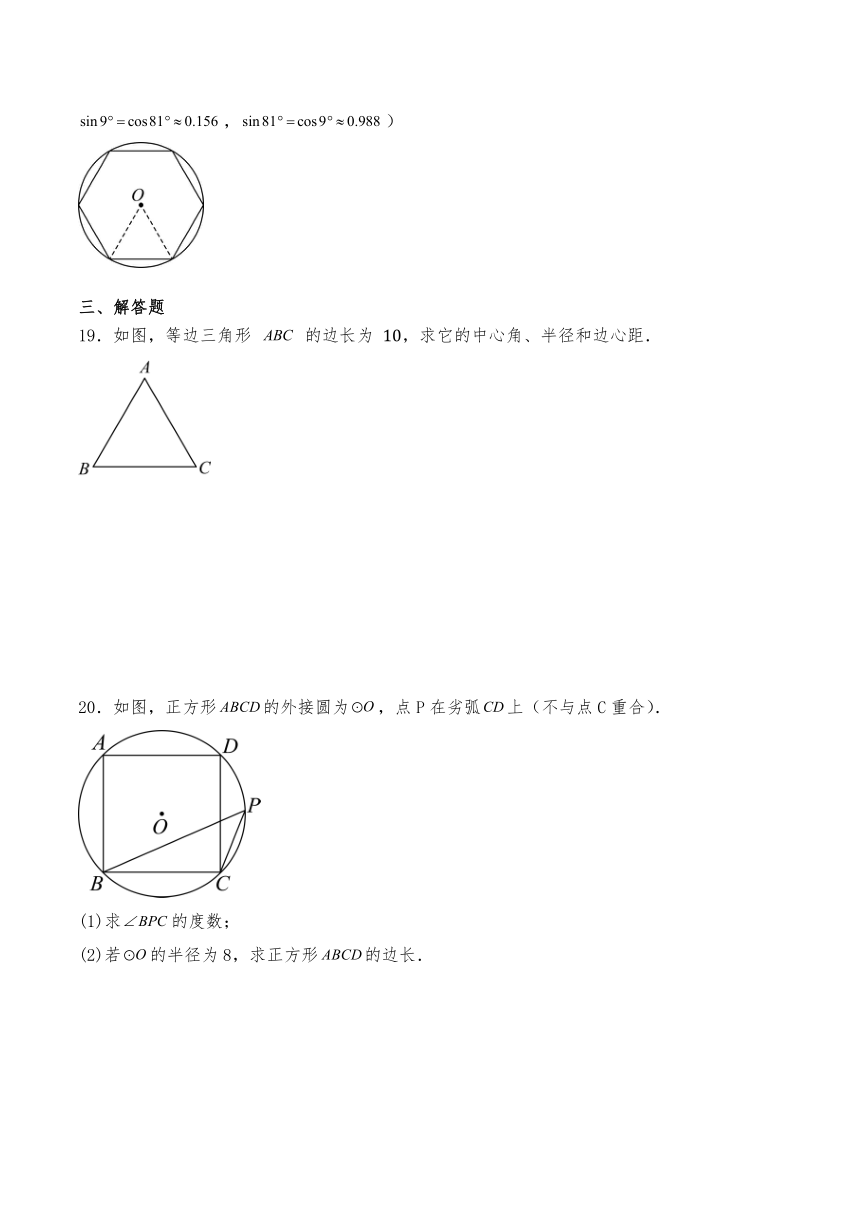
20.如图,正方形的外接圆为,点P在劣弧上(不与点C重合).
(1)求的度数;
(2)若的半径为8,求正方形的边长.
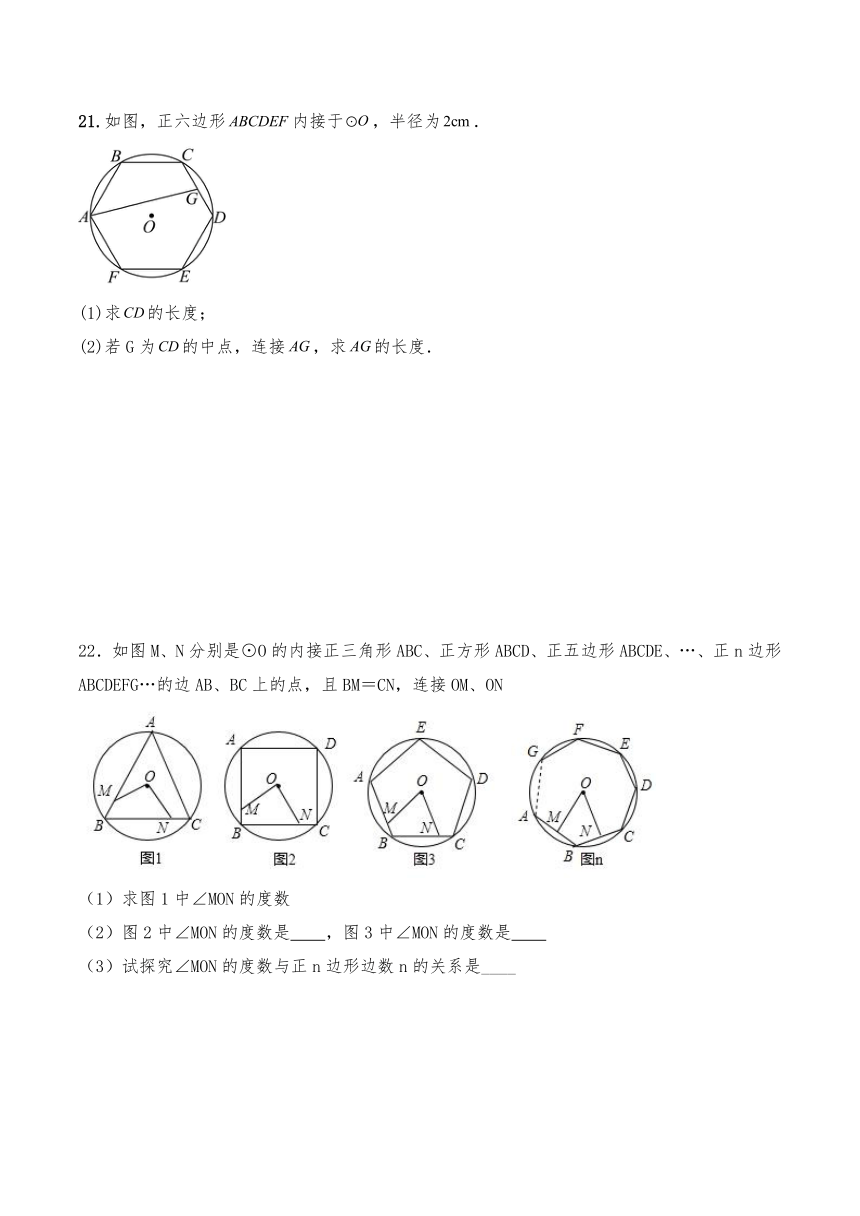
21.如图,正六边形内接于,半径为.
(1)求的长度;
(2)若G为的中点,连接,求的长度.
22.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
答案
一、单选题
1.B
【分析】根据正多边形的中心角和为360°和正多边形的中心角相等,列式计算可求出这个多边形的边数,然后根据多边形的内角和公式(n-2)×180°可得出结果.
【解析】解:根据题意可得,这个多边形的边数为:360÷72=5,
∴这个多边形的内角和为:(5-2)×180°=540°.
故选:B.
2.A
【分析】设正六边形的中心是O,一边是AB,过O作OG⊥AB与G,在直角△OAG中,根据三角函数即可求得OA.
【解析】如图,
在Rt△AOG中,OG=,∠AOG=30°,
∴OA=OG÷cos 30°==2;
故选A.
3.C
【分析】正边形的内角和为,则它的内角等于,边形的中心角等于,根据中心角等于内角就可以得到一个关于的方程,解方程即可得答案.
【解析】∵正边形的内角和为,
∴它的内角等于,中心角等于,
∵中心角等于内角,
∴=,
解得:,即这个多边形是正四边形.
故选:C.
4.C
【分析】如图,画出图形,在直角三角形OAM中,直接利用三角函数即可得到OA.
【解析】如图,正十边形的中心角∠AOB=360°÷10=36°,AB=a
∴∠AOM=∠BOM=18°,AM=MB=a;
∴OA==
故选C.
5.B
【分析】如图,画出简图,根据切线的性质可得∠OCA=90°,根据∠AOC的余弦可得∠AOC=45°,即可得出此多边形的中心角为90°,即可求出多边形的边数.
【解析】如图,OA、OC分别为此多边形的外接圆和内切圆的半径,AB为边长,
∴OC⊥AB,
∴∠OCA=90°,
∵外接圆半径是其内切圆半径的倍,
∴cos∠AOC==,
∴∠AOC=45°,
∴∠AOB=90°,即此多边形的中心角为90°,
∴此多边形的边数=360°÷90°=4,
故选:B.
6.D
【分析】根据题意画出图形,然后由三角函数及正多边形与圆的关系进行求解即可.
【解析】解:由题意可得如图:
假设AB为正n多边形的一条边,OC⊥AB,
,
OA=r,
;
故选D.
7.B
【解析】试题分析:根据正多边形的中心角与边数的关系,其边数为.
考点:正多边形的中心角定义及求法.
8.C
【分析】根据题意可以求出这个正n边形的中心角是60°,即可求出边数.
【解析】⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,
则这个正n边形的中心角是60°,
n的值为6,
故选C
9.D
【解析】解:连接OB,
∵OB=4,
∴BM=2,
∴OM=2,,
故选D.
10.D
【分析】设正六边形的边长为a,MN是△PCD的中位线,求出△PBM和△PCD的面积即可.
【解析】解:设正六边形的边长为a,连接AC交BE于H点,如下图所示:
正六边形六边均相等,且每个内角为120°,
∴△ABC为30°,30°,120°等腰三角形,
∴BE⊥AC,且,且,
∵AF∥CD,P为AF上一点,
∴,
MN为△PCD的中位线,
∴,
由正六边形的对称性可知:,
∴,
∴,
∴,
故选:D.
二、填空题
11.
【分析】本题考查了正多边形的内角和、边数、中心角,先根据正多边形的内角和求出边数,再求其中心角的度数即可.
【解析】解:设这个正多边形的边数为,
由题意得,,
解得,
正六边形的中心角是,
故答案为:.
12.
【分析】正八边形的面积有八个全等的等腰三角形面积组成,计算一个等腰三角形的面积,乘以8即可.
【解析】解:过A作AM⊥OB于M,
如图所示,△ABO为等腰三角形,OA=OB=6,∠AOB=,
∵AM是OB上的高,
∴∠AOM=∠OAM=45°,
∴OM=AM,
∴sin45°=,
∴AM=,
∴,
∴正八边形的面积为:.
故答案为.
13.
【分析】本题考查了正多边形和外接圆、锐角三角函数,掌握正多边形外接圆的半径、边长、边心距、中心角之间的计算转化为解直角三角形,熟知是解答本题的关键.由一个正多边形的外角为,可得正五边形,然后根据边心距为2,结合锐角三角函数求出外接圆的半径,再通过圆的面积公式计算即可.
【解析】解:∵一个正多边形的外角为,
∴
∴这个正多边形是五边形,
如图,过正五边形的中心O作于D,连接,,
∵边心距为2,
∴,
∵,,
∴,
在中,∵,
∴,则,
∴外接圆的面积为,
故答案为:.
14.
【分析】本题考查解直角三角形,正多边形的性质,画出图形,设,利用三角函数即可求解.
【解析】∵正多边形无对角线,
∴该正多边形是等边三角形,如图所示
∴
设,则
∴,
∴正多边形外接圆直径与自身边长之比为
故答案为:.
15.
【分析】本题考查了正多边形的对角线条数公式,正多边形的中心角,等腰三角形的性质,相似三角形的判定和性质,锐角三角函数,根据题意判断出对角线条数和边数相同的正多边形是正五边形,然后构造三角形相似来求解是解题的关键.先利用正多边形的对角线条数公式求出符合题意的正多边形为正五边形,然后求出正五边形的中心角为,再作等腰,使顶角,则底角,作的角平分线,过点作于,则可得到,设,,则,,证明,得到,即,进而得到,在中,利用余弦的定义即可得解.
【解析】解:设正多边形的边数为,则对角线条数为,
根据题意得,,解得,或(舍去)
对角线条数和边数相同的正多边形是正五边形,正五边形的中心角为,
如图,作等腰,使顶角,则底角,作的角平分线,过点作于,
则,
,
,,
,,
,
,,
,,
设,,则,,
,,
,
,即,
整理得:,
,即,
,
,
在中,,
故答案为:.
16.
【分析】此题考查了正八边形与圆,正多边形的性质应用是解题的关键.设正八边形中心为点O,连接,求出中心角,设,得到,即可得到答案.
【解析】解:设正八边形中心为点O,连接,如图,
∵多边形为正八边形,
∴中心角,
设,
∴
∴,
故答案为:
17.
【分析】本题考查正多边形和圆,掌握正六边形的性质,直角三角形的边角关系以及锐角三角函数的定义是正确解答的关键.连接,过点作,垂足为E,
根据正六边形的性质,直角三角形的边角关系以及锐角三角函数的定义进行计算即可.
【解析】解:如图,连接,过点作,垂足为E,
设正六边形的边长为a,则,
在中,,
∴,,
∴,
∴.
故答案为:.
18.3.12
【分析】本题主要考查了正多边形和圆以及解直角三角形的运用,圆的内接正二十边形被半径分成顶角为的二十个等腰三角形,作辅助线构造直角三角形,根据中心角的度数以及半径的大小,求得,,进而得到答案.
【解析】解:如图,圆的内接正二十边形被半径分成20个如图所示的等腰三角形,
其顶角为,即,
作于点H,则,
,
在中,,即,
,
,
,
,
,
故答案为:.
三、解答题
19.解:如图,
设等边三角形 的中心为点 ,过点 作 于点 ,连接 ,,则 ,,.
.
.
设 ,则 .
在 中,,
即 .
解得 (负值已舍去).
,.
等边三角形 的中心角为 ,半径为 ,边心距为 .
20.(1)解:连接,
由题意得:,
∴;
(2)由(1)知:,
又∵,
∴,
即正方形的边长为:.
21.(1)解:连接,,如图:
六边形是正六边形,
,
又,是的半径,且半径为,
,
是等边三角形,
.
(2)连接,,如图:
则为的直径,
,,
由(1)得:,
在中,,
,
G为的中点,
,
在中,,
.
22.(1)如图,连接OB、OC,则,
是内接正三角形,
中心角∠BOC==120 ,
∵点O是内接正三角形ABC的内心,
∴,
∴,
在和中,,
∴,
∴,
∴,
故答案为:;
(2)如图1,连接OB、OC,
四边形ABCD是内接正方形,
中心角,
同(1)的方法可证:;
如图2,连接OB、OC,
五边形ABCDE是内接正五边形,
中心角,
同(1)的方法可证:,
故答案为:,;
(3)由上可知,的度数与正三角形边数的关系是,
的度数与正方形边数的关系是,
的度数与正五边形边数的关系是,
归纳类推得:的度数与正n边形边数n的关系是,
故答案为:.
一、单选题
1.如果一个正多边形的中心角等于,那么这个多边形的内角和为( )
A. B. C. D.
2.已知正六边形的边心距为,则它的半径为( )
A.2 B.4 C.2 D.4
3.下列正多边形中,中心角等于内角的是( )
A.正六边形 B.正五边形 C.正四边形 D.正三边形
4.如果正十边形的边长为a,那么它的半径是( )
A. B. C. D.
5.如果某正多边形的外接圆半径是其内切圆半径的倍,那么这个正多边形的边数是( )
A.3 B.4 C.5 D.无法确定
6.若一个正n边形(n为大于2的整数)的半径为r,则这个正n变形的边心距为( )
A. B. C. D.
7.如果一个正多边形的中心角为,那么这个正多边形的边数是( ).
A. B. C. D.
8.⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则n的值为( )
A.3 B.4 C.6 D.8
9.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
A.2, B.2 ,π C., D.2,
10.如图,六边形是正六边形,点是边的中点,,分别与交于点,,则的值为( ).
A. B. C. D.
二、填空题
11.如果一个正多边形的内角和是720°,那么它的中心角是 度.
12.正八边形的半径为6,则正八边形的面积为 .
13.已知一个正多边形的外角为,他的边心距为2,则它外接圆的面积为
14.若一个正多边形无对角线,则这个正多边形外接圆直径与自身边长之比为
15.对角线条数和边数相同的正多边形的中心角的余弦值为
16.如图,是正八边形的两条对角线,则 .
17.如图,两个边长相等的正六边形的公共边为,点A,B,C在同一直线上, 点,分别为两个正六边形的中心. 则的值为 .
18.中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,由此求得圆周率的近似值.例如:设半径为r的圆内接正n边形的周长为C,圆的直径为d,如图,当时,,当时, .(结果精确到0.01,参考数据:,)
三、解答题
19.如图,等边三角形 的边长为 ,求它的中心角、半径和边心距.
20.如图,正方形的外接圆为,点P在劣弧上(不与点C重合).
(1)求的度数;
(2)若的半径为8,求正方形的边长.
21.如图,正六边形内接于,半径为.
(1)求的长度;
(2)若G为的中点,连接,求的长度.
22.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
答案
一、单选题
1.B
【分析】根据正多边形的中心角和为360°和正多边形的中心角相等,列式计算可求出这个多边形的边数,然后根据多边形的内角和公式(n-2)×180°可得出结果.
【解析】解:根据题意可得,这个多边形的边数为:360÷72=5,
∴这个多边形的内角和为:(5-2)×180°=540°.
故选:B.
2.A
【分析】设正六边形的中心是O,一边是AB,过O作OG⊥AB与G,在直角△OAG中,根据三角函数即可求得OA.
【解析】如图,
在Rt△AOG中,OG=,∠AOG=30°,
∴OA=OG÷cos 30°==2;
故选A.
3.C
【分析】正边形的内角和为,则它的内角等于,边形的中心角等于,根据中心角等于内角就可以得到一个关于的方程,解方程即可得答案.
【解析】∵正边形的内角和为,
∴它的内角等于,中心角等于,
∵中心角等于内角,
∴=,
解得:,即这个多边形是正四边形.
故选:C.
4.C
【分析】如图,画出图形,在直角三角形OAM中,直接利用三角函数即可得到OA.
【解析】如图,正十边形的中心角∠AOB=360°÷10=36°,AB=a
∴∠AOM=∠BOM=18°,AM=MB=a;
∴OA==
故选C.
5.B
【分析】如图,画出简图,根据切线的性质可得∠OCA=90°,根据∠AOC的余弦可得∠AOC=45°,即可得出此多边形的中心角为90°,即可求出多边形的边数.
【解析】如图,OA、OC分别为此多边形的外接圆和内切圆的半径,AB为边长,
∴OC⊥AB,
∴∠OCA=90°,
∵外接圆半径是其内切圆半径的倍,
∴cos∠AOC==,
∴∠AOC=45°,
∴∠AOB=90°,即此多边形的中心角为90°,
∴此多边形的边数=360°÷90°=4,
故选:B.
6.D
【分析】根据题意画出图形,然后由三角函数及正多边形与圆的关系进行求解即可.
【解析】解:由题意可得如图:
假设AB为正n多边形的一条边,OC⊥AB,
,
OA=r,
;
故选D.
7.B
【解析】试题分析:根据正多边形的中心角与边数的关系,其边数为.
考点:正多边形的中心角定义及求法.
8.C
【分析】根据题意可以求出这个正n边形的中心角是60°,即可求出边数.
【解析】⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,
则这个正n边形的中心角是60°,
n的值为6,
故选C
9.D
【解析】解:连接OB,
∵OB=4,
∴BM=2,
∴OM=2,,
故选D.
10.D
【分析】设正六边形的边长为a,MN是△PCD的中位线,求出△PBM和△PCD的面积即可.
【解析】解:设正六边形的边长为a,连接AC交BE于H点,如下图所示:
正六边形六边均相等,且每个内角为120°,
∴△ABC为30°,30°,120°等腰三角形,
∴BE⊥AC,且,且,
∵AF∥CD,P为AF上一点,
∴,
MN为△PCD的中位线,
∴,
由正六边形的对称性可知:,
∴,
∴,
∴,
故选:D.
二、填空题
11.
【分析】本题考查了正多边形的内角和、边数、中心角,先根据正多边形的内角和求出边数,再求其中心角的度数即可.
【解析】解:设这个正多边形的边数为,
由题意得,,
解得,
正六边形的中心角是,
故答案为:.
12.
【分析】正八边形的面积有八个全等的等腰三角形面积组成,计算一个等腰三角形的面积,乘以8即可.
【解析】解:过A作AM⊥OB于M,
如图所示,△ABO为等腰三角形,OA=OB=6,∠AOB=,
∵AM是OB上的高,
∴∠AOM=∠OAM=45°,
∴OM=AM,
∴sin45°=,
∴AM=,
∴,
∴正八边形的面积为:.
故答案为.
13.
【分析】本题考查了正多边形和外接圆、锐角三角函数,掌握正多边形外接圆的半径、边长、边心距、中心角之间的计算转化为解直角三角形,熟知是解答本题的关键.由一个正多边形的外角为,可得正五边形,然后根据边心距为2,结合锐角三角函数求出外接圆的半径,再通过圆的面积公式计算即可.
【解析】解:∵一个正多边形的外角为,
∴
∴这个正多边形是五边形,
如图,过正五边形的中心O作于D,连接,,
∵边心距为2,
∴,
∵,,
∴,
在中,∵,
∴,则,
∴外接圆的面积为,
故答案为:.
14.
【分析】本题考查解直角三角形,正多边形的性质,画出图形,设,利用三角函数即可求解.
【解析】∵正多边形无对角线,
∴该正多边形是等边三角形,如图所示
∴
设,则
∴,
∴正多边形外接圆直径与自身边长之比为
故答案为:.
15.
【分析】本题考查了正多边形的对角线条数公式,正多边形的中心角,等腰三角形的性质,相似三角形的判定和性质,锐角三角函数,根据题意判断出对角线条数和边数相同的正多边形是正五边形,然后构造三角形相似来求解是解题的关键.先利用正多边形的对角线条数公式求出符合题意的正多边形为正五边形,然后求出正五边形的中心角为,再作等腰,使顶角,则底角,作的角平分线,过点作于,则可得到,设,,则,,证明,得到,即,进而得到,在中,利用余弦的定义即可得解.
【解析】解:设正多边形的边数为,则对角线条数为,
根据题意得,,解得,或(舍去)
对角线条数和边数相同的正多边形是正五边形,正五边形的中心角为,
如图,作等腰,使顶角,则底角,作的角平分线,过点作于,
则,
,
,,
,,
,
,,
,,
设,,则,,
,,
,
,即,
整理得:,
,即,
,
,
在中,,
故答案为:.
16.
【分析】此题考查了正八边形与圆,正多边形的性质应用是解题的关键.设正八边形中心为点O,连接,求出中心角,设,得到,即可得到答案.
【解析】解:设正八边形中心为点O,连接,如图,
∵多边形为正八边形,
∴中心角,
设,
∴
∴,
故答案为:
17.
【分析】本题考查正多边形和圆,掌握正六边形的性质,直角三角形的边角关系以及锐角三角函数的定义是正确解答的关键.连接,过点作,垂足为E,
根据正六边形的性质,直角三角形的边角关系以及锐角三角函数的定义进行计算即可.
【解析】解:如图,连接,过点作,垂足为E,
设正六边形的边长为a,则,
在中,,
∴,,
∴,
∴.
故答案为:.
18.3.12
【分析】本题主要考查了正多边形和圆以及解直角三角形的运用,圆的内接正二十边形被半径分成顶角为的二十个等腰三角形,作辅助线构造直角三角形,根据中心角的度数以及半径的大小,求得,,进而得到答案.
【解析】解:如图,圆的内接正二十边形被半径分成20个如图所示的等腰三角形,
其顶角为,即,
作于点H,则,
,
在中,,即,
,
,
,
,
,
故答案为:.
三、解答题
19.解:如图,
设等边三角形 的中心为点 ,过点 作 于点 ,连接 ,,则 ,,.
.
.
设 ,则 .
在 中,,
即 .
解得 (负值已舍去).
,.
等边三角形 的中心角为 ,半径为 ,边心距为 .
20.(1)解:连接,
由题意得:,
∴;
(2)由(1)知:,
又∵,
∴,
即正方形的边长为:.
21.(1)解:连接,,如图:
六边形是正六边形,
,
又,是的半径,且半径为,
,
是等边三角形,
.
(2)连接,,如图:
则为的直径,
,,
由(1)得:,
在中,,
,
G为的中点,
,
在中,,
.
22.(1)如图,连接OB、OC,则,
是内接正三角形,
中心角∠BOC==120 ,
∵点O是内接正三角形ABC的内心,
∴,
∴,
在和中,,
∴,
∴,
∴,
故答案为:;
(2)如图1,连接OB、OC,
四边形ABCD是内接正方形,
中心角,
同(1)的方法可证:;
如图2,连接OB、OC,
五边形ABCDE是内接正五边形,
中心角,
同(1)的方法可证:,
故答案为:,;
(3)由上可知,的度数与正三角形边数的关系是,
的度数与正方形边数的关系是,
的度数与正五边形边数的关系是,
归纳类推得:的度数与正n边形边数n的关系是,
故答案为:.
