小学数学北师大版(2024)六年级下圆锥的体积课件(共27张PPT)
文档属性
| 名称 | 小学数学北师大版(2024)六年级下圆锥的体积课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-26 05:31:57 | ||
图片预览






文档简介
(共27张PPT)
《圆锥的体积》
北师大版六年级下册
圆柱与圆锥
01 情景导入与知识引入
通过生活实例引入圆锥体积的概念
计算圆锥形小麦堆的体积
看,这堆小麦堆得像小山一样,小麦丰收了!你知道这堆小麦的体积大约是多少吗?让我们来计算一下吧。
圆锥的体积与哪种图形有关?
回想已知图形
你还记得我们学过的其他图形的体积公式吗?例如,长方体和圆柱体。
观察与思考
思考一下,圆锥体积可能与哪个图形的体积有关呢?
猜想与验证
现在,尝试猜想一下,圆锥体积和哪个图形的体积有关系,再通过实验去验证。
02
圆锥体积公式推导探究
理解圆锥体积的来龙去脉
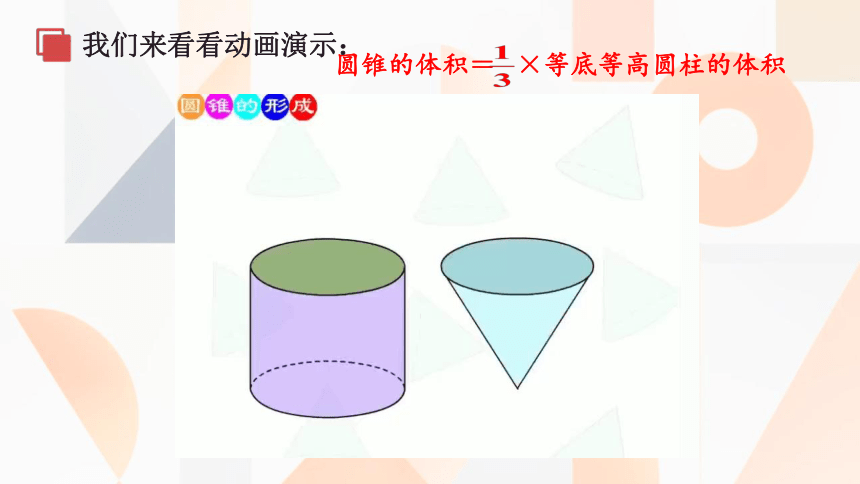
圆锥的体积和它等底同高的圆柱的体积会有什么关系呢?
我们来看看动画演示:
圆锥的体积= ×等底等高圆柱的体积
推导圆锥体积公式
通过实验结果,我们可以得出:圆锥体积等于三分之一的圆柱体积,即 V = πr h。
S
h
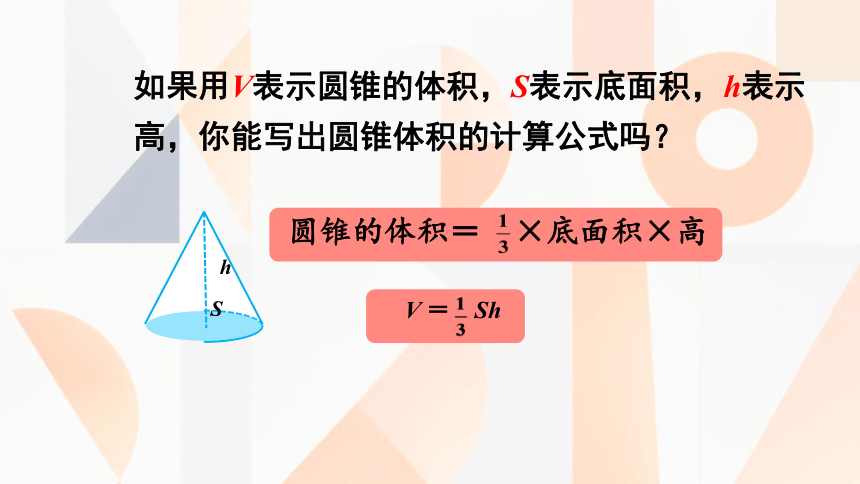
圆锥的体积= ×底面积×高
V = Sh
如果用V表示圆锥的体积,S表示底面积,h表示高,你能写出圆锥体积的计算公式吗?
03
实例大挑战:圆锥体积知识应用
用实例加深对圆锥体积的理解与运用
沙堆谜题:圆锥体积与重量计算
问题提出
工地上有一堆近似圆锥的沙子,已知底面直径4m,高1.5m,每立方米沙子重1.5吨,求沙堆体积和重量。
计算底面积
先求底面半径:4÷2 = 2m,再算底面积:3.14×2 = 12.56 m 。
计算体积
根据圆锥体积公式V = Sh,可得体积: ×12.56×1.5 = 6.28 m 。
计算重量
已知每立方米沙子重1.5吨,沙堆重量:6.28×1.5 = 9.42吨。
1
3
1
3
挑战自我:巩固圆锥体积公式应用
1.下图中,圆锥的体积与哪个圆柱的体积相等?说说你是怎
么想的。
15
6
6
6
2
2
5
2.计算下面各圆锥的体积。
【选自教材P12 练一练 第2题】
3.如图,测量中经常使用铅锤。这个铅锤的体积是多少立方
厘米?(结果保留2位小数)。
答:这个铅锤的体积是16.75立方厘米。
【选自教材P12 练一练 第3题】
4. 有一顶圆锥形帐篷,底面直径约5m,高约3.6m。
(1)它的占地面积约是多少平方米?
(2)它的体积约是多少立方米?
(1)3.14×(5÷2)2=19.625(m2)
(2) ×19.625×3.6=23.55(m3)
答:它的占地面积约是19.625平方米。
它的体积约是23.55立方米。
【选自教材P12 练一练 第4题】
5.张大伯家有一堆小麦,堆成了圆锥形,张大伯量得它的底面周
长是9.42m,高是2m,这堆小麦的体积是多少立方米?如果每
立方米小麦的质量为700kg,这堆小麦的质量为多少千克?
底面积:3.14×(9.42÷3.14÷2)2=7.065(m2)
体积:
质量:
4.71×700=3297(kg)
答:这堆小麦的体积是4.71立方米。
这堆小麦的质量为3297千克。
【选自教材P12 练一练 第5题】
6. 一个圆柱形橡皮泥,底面积是12cm2,高是5cm。
(1)如果把它捏成同样底面大小的圆锥,这个圆锥的高是多少?
因为体积不变,底面积也不变,
所以圆锥的高应是圆柱的3倍,圆锥的高应是15cm。
【选自教材P12 练一练 第6题】
因为体积不变,高不变,
所以圆锥的底面积应是圆柱的3倍,
圆锥的底面面积是36 cm2。
6. 一个圆柱形橡皮泥,底面积是12cm2,高是5cm。
(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
【选自教材P12 练一练 第6题】
04
课堂练习与互动巩固
通过练习和互动,巩固圆锥体积知识
圆锥体积小挑战
填空挑战
1. 圆柱的体积是 9 cm ,与它等底等高的圆锥体积是( )。
2. 圆锥的底面积 5.4 m ,高 21 m ,体积是( )。
判断挑战
1. 圆锥的体积等于圆柱体积的 3 倍。( )
2. 圆锥的体积等于和它等底等高的圆柱体积的 1/3 。( )
1
2
05
跨学科拓展与课堂总结
将数学应用于生活中的各个方面,提升学习兴趣。
蚁狮的圆锥形洞穴
蚁狮会挖出圆锥形的洞穴作为陷阱,并在洞穴中等待捕捉掉进陷阱中的蚂蚁和其他昆虫。通过这节内容,学生能够将课堂上学到的圆锥体积知识应用到实际的生活现象中。
圆锥体积总结
S
h
圆锥的体积= ×底面积×高
V = Sh
通过这节课的学习活动,你有什么收获?
06
作业布置与知识延伸
通过作业和延伸任务,巩固学生对圆锥体积的理解
圆锥体积计算书面作业
1
作业题目1
一个圆锥形的零件,底面积是 19 cm ,高是 12 cm。这个零件的体积是多少?
2
作业题目2
一个用铜铸造的圆锥形铜锤,底面直径是4cm,高是6cm。每立方厘米铜大约重7.9g。这个铜锤大约重多少克?(得数保留整数。)
生活中的圆锥体积应用
实例查找任务
请同学们在生活中查找一些圆锥形物体,比如冰淇淋筒、沙堆等,记录下这些物体的尺寸,并计算其体积。
体积应用分析
分析找到的圆锥体积在实际生活中的应用场景,如沙堆的重量计算、食物包装等。
分享与交流
将你找到的圆锥形物体和计算结果在课堂上与同学们分享,并讨论这些物体的实际用途。
谢谢聆听
《圆锥的体积》
北师大版六年级下册
圆柱与圆锥
01 情景导入与知识引入
通过生活实例引入圆锥体积的概念
计算圆锥形小麦堆的体积
看,这堆小麦堆得像小山一样,小麦丰收了!你知道这堆小麦的体积大约是多少吗?让我们来计算一下吧。
圆锥的体积与哪种图形有关?
回想已知图形
你还记得我们学过的其他图形的体积公式吗?例如,长方体和圆柱体。
观察与思考
思考一下,圆锥体积可能与哪个图形的体积有关呢?
猜想与验证
现在,尝试猜想一下,圆锥体积和哪个图形的体积有关系,再通过实验去验证。
02
圆锥体积公式推导探究
理解圆锥体积的来龙去脉
圆锥的体积和它等底同高的圆柱的体积会有什么关系呢?
我们来看看动画演示:
圆锥的体积= ×等底等高圆柱的体积
推导圆锥体积公式
通过实验结果,我们可以得出:圆锥体积等于三分之一的圆柱体积,即 V = πr h。
S
h
圆锥的体积= ×底面积×高
V = Sh
如果用V表示圆锥的体积,S表示底面积,h表示高,你能写出圆锥体积的计算公式吗?
03
实例大挑战:圆锥体积知识应用
用实例加深对圆锥体积的理解与运用
沙堆谜题:圆锥体积与重量计算
问题提出
工地上有一堆近似圆锥的沙子,已知底面直径4m,高1.5m,每立方米沙子重1.5吨,求沙堆体积和重量。
计算底面积
先求底面半径:4÷2 = 2m,再算底面积:3.14×2 = 12.56 m 。
计算体积
根据圆锥体积公式V = Sh,可得体积: ×12.56×1.5 = 6.28 m 。
计算重量
已知每立方米沙子重1.5吨,沙堆重量:6.28×1.5 = 9.42吨。
1
3
1
3
挑战自我:巩固圆锥体积公式应用
1.下图中,圆锥的体积与哪个圆柱的体积相等?说说你是怎
么想的。
15
6
6
6
2
2
5
2.计算下面各圆锥的体积。
【选自教材P12 练一练 第2题】
3.如图,测量中经常使用铅锤。这个铅锤的体积是多少立方
厘米?(结果保留2位小数)。
答:这个铅锤的体积是16.75立方厘米。
【选自教材P12 练一练 第3题】
4. 有一顶圆锥形帐篷,底面直径约5m,高约3.6m。
(1)它的占地面积约是多少平方米?
(2)它的体积约是多少立方米?
(1)3.14×(5÷2)2=19.625(m2)
(2) ×19.625×3.6=23.55(m3)
答:它的占地面积约是19.625平方米。
它的体积约是23.55立方米。
【选自教材P12 练一练 第4题】
5.张大伯家有一堆小麦,堆成了圆锥形,张大伯量得它的底面周
长是9.42m,高是2m,这堆小麦的体积是多少立方米?如果每
立方米小麦的质量为700kg,这堆小麦的质量为多少千克?
底面积:3.14×(9.42÷3.14÷2)2=7.065(m2)
体积:
质量:
4.71×700=3297(kg)
答:这堆小麦的体积是4.71立方米。
这堆小麦的质量为3297千克。
【选自教材P12 练一练 第5题】
6. 一个圆柱形橡皮泥,底面积是12cm2,高是5cm。
(1)如果把它捏成同样底面大小的圆锥,这个圆锥的高是多少?
因为体积不变,底面积也不变,
所以圆锥的高应是圆柱的3倍,圆锥的高应是15cm。
【选自教材P12 练一练 第6题】
因为体积不变,高不变,
所以圆锥的底面积应是圆柱的3倍,
圆锥的底面面积是36 cm2。
6. 一个圆柱形橡皮泥,底面积是12cm2,高是5cm。
(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
【选自教材P12 练一练 第6题】
04
课堂练习与互动巩固
通过练习和互动,巩固圆锥体积知识
圆锥体积小挑战
填空挑战
1. 圆柱的体积是 9 cm ,与它等底等高的圆锥体积是( )。
2. 圆锥的底面积 5.4 m ,高 21 m ,体积是( )。
判断挑战
1. 圆锥的体积等于圆柱体积的 3 倍。( )
2. 圆锥的体积等于和它等底等高的圆柱体积的 1/3 。( )
1
2
05
跨学科拓展与课堂总结
将数学应用于生活中的各个方面,提升学习兴趣。
蚁狮的圆锥形洞穴
蚁狮会挖出圆锥形的洞穴作为陷阱,并在洞穴中等待捕捉掉进陷阱中的蚂蚁和其他昆虫。通过这节内容,学生能够将课堂上学到的圆锥体积知识应用到实际的生活现象中。
圆锥体积总结
S
h
圆锥的体积= ×底面积×高
V = Sh
通过这节课的学习活动,你有什么收获?
06
作业布置与知识延伸
通过作业和延伸任务,巩固学生对圆锥体积的理解
圆锥体积计算书面作业
1
作业题目1
一个圆锥形的零件,底面积是 19 cm ,高是 12 cm。这个零件的体积是多少?
2
作业题目2
一个用铜铸造的圆锥形铜锤,底面直径是4cm,高是6cm。每立方厘米铜大约重7.9g。这个铜锤大约重多少克?(得数保留整数。)
生活中的圆锥体积应用
实例查找任务
请同学们在生活中查找一些圆锥形物体,比如冰淇淋筒、沙堆等,记录下这些物体的尺寸,并计算其体积。
体积应用分析
分析找到的圆锥体积在实际生活中的应用场景,如沙堆的重量计算、食物包装等。
分享与交流
将你找到的圆锥形物体和计算结果在课堂上与同学们分享,并讨论这些物体的实际用途。
谢谢聆听
