1.2 30° 45° 60°角的三角函数值 同步练习(含答案)2024-2025学年北师大版数学九年级下册
文档属性
| 名称 | 1.2 30° 45° 60°角的三角函数值 同步练习(含答案)2024-2025学年北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 09:14:08 | ||
图片预览


文档简介
1.2 30°45°60°角的三角函数值
一、单选题
1.下列三角函数的值是的是( )
A. B. C. D.
2.在锐角中,若,则等于( )
A. B. C. D.
3.设,则下列式子成立的是( )
A. B.
C. D.
4.计算的值为( )
A. B. C. D.
5.正方形网格中,如图放置,则的值为( )
A. B. C.1 D.
6.在中,,,则( )
A. B. C. D.
7.三角板是我们数学学习中必不可少的工具,利用三角板可以拼出很多角,现将一副含45°角和30°角的三角板按如图所示的方式放置,则的值为( )
A. B. C. D.无法确定
8.的值等于( )
A.1 B. C. D.2
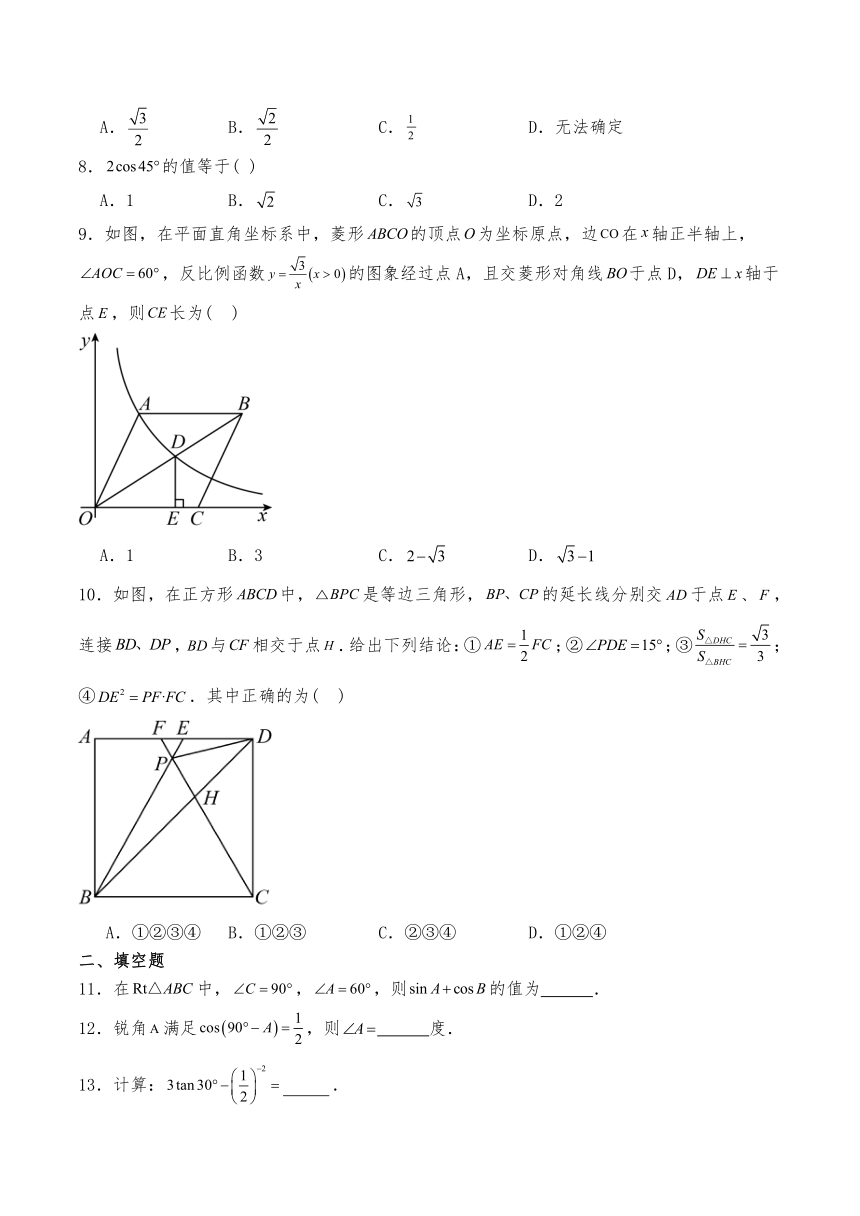
9.如图,在平面直角坐标系中,菱形的顶点为坐标原点,边在轴正半轴上,,反比例函数的图象经过点A,且交菱形对角线于点D,轴于点,则长为( )
A.1 B.3 C. D.
10.如图,在正方形中,是等边三角形,的延长线分别交于点、,连接,与相交于点.给出下列结论:①;②;③;④.其中正确的为( )
A.①②③④ B.①②③ C.②③④ D.①②④
二、填空题
11.在中,,,则的值为 .
12.锐角满足,则 度.
13.计算:.
14. .
15.若的余角是,则的值是 .
16.如图,在菱形中,.点分别为四边的中点,连接,则 .
17.如图,一块含有的直角三角板的直角顶点和坐标原点O重合,角的顶点A在反比例函数的图象上,顶点B在反比例函数的图象上,则k的值为 .
18.如图,等边中,点D在上,点E在上,,连接、交于点F,,,则的长为 .
三、解答题
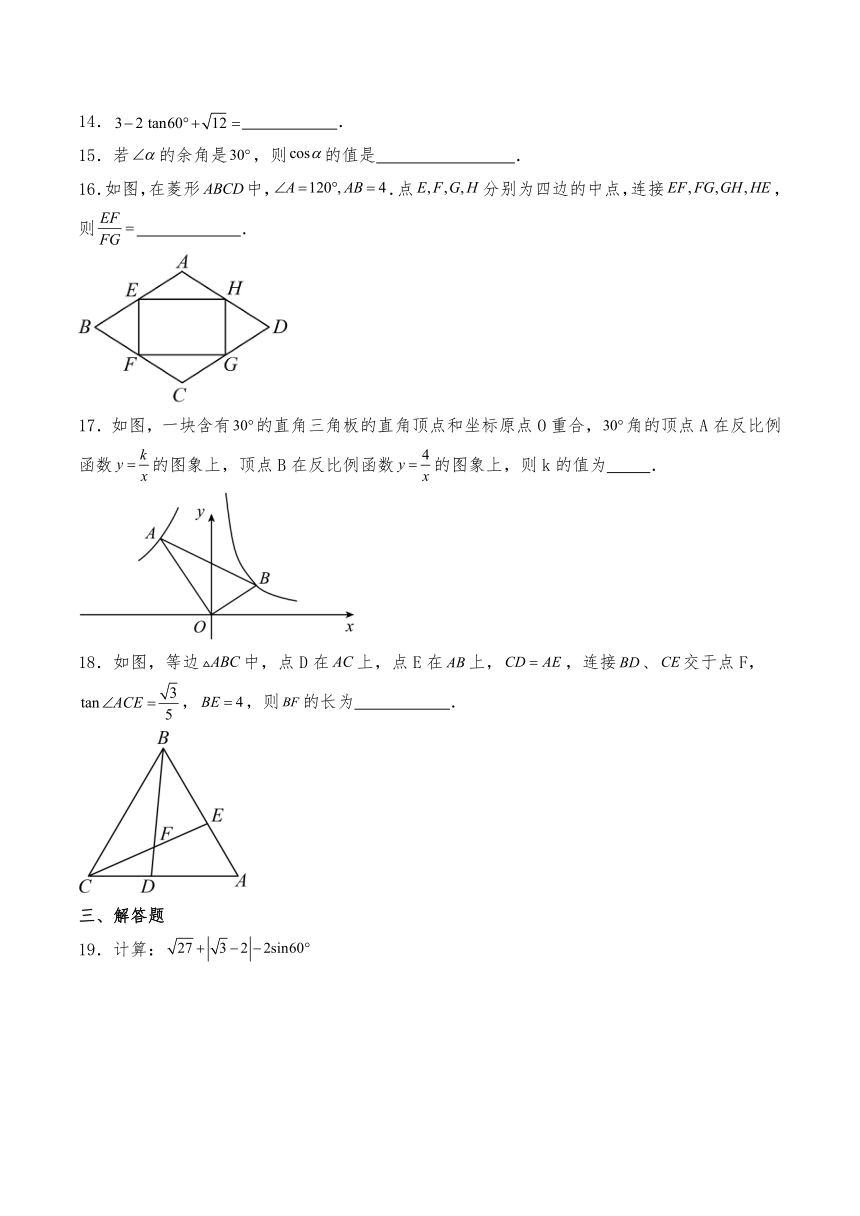
19.计算:
20.计算:
21.计算:.
22.先化简,再求代数式的值,其中.
23.先化简,再求代数式的值,其中.
24.如图,已知,.
(1)求证:;
(2)若,,求.
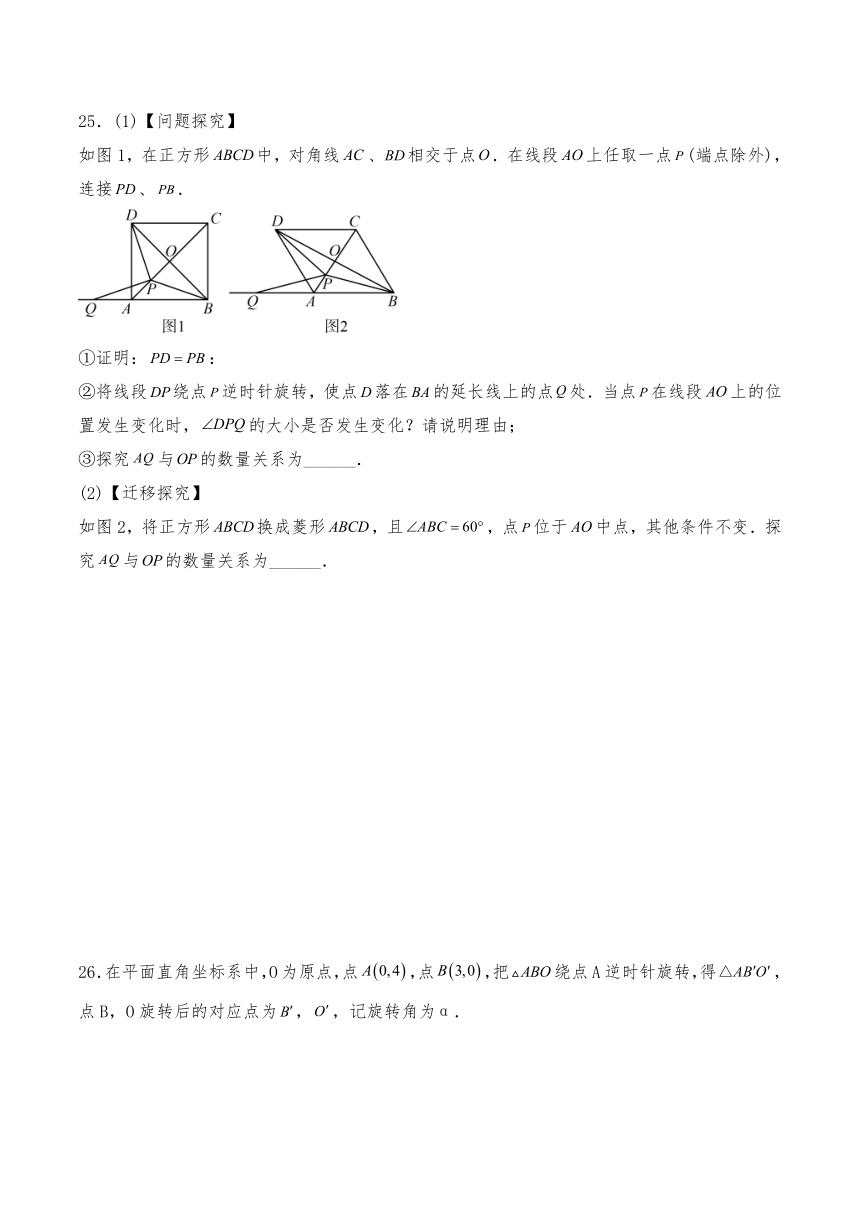
25.(1)【问题探究】
如图1,在正方形中,对角线、相交于点.在线段上任取一点(端点除外),连接、.
①证明::
②将线段绕点逆时针旋转,使点落在的延长线上的点处.当点在线段上的位置发生变化时,的大小是否发生变化?请说明理由;
③探究与的数量关系为______.
(2)【迁移探究】
如图2,将正方形换成菱形,且,点位于中点,其他条件不变.探究与的数量关系为______.
26.在平面直角坐标系中,O为原点,点,点,把绕点A逆时针旋转,得,点B,O旋转后的对应点为,,记旋转角为α.
(1)如图1,若,连接,求的长度;
(2)如图2,若,求的坐标并直接写出的坐标;
(3)在(2)的条件下,边上的一点P旋转后的对应点为,请直接写出的最小值和此时点P的坐标.
答案
一、单选题
1.A
【分析】根据特殊角的三角函数值解答.
【详解】解:,,, ,
观察四个选项,选项A符合题意,
故选:A.
2.A
【分析】根据平方及绝对值的非负性可得,,由特殊角的三角函数值求得和,再由三角形内角和为即可解答;
【详解】解:∵,
∴,,
∴,,
∴在锐角中,,
故选: A;
3.C
【分析】根据的取值范围选择特殊值,然后求出正弦、余弦、正切的值,进行比较即可得到答案.
【详解】解:,
取,
,,,
,
,
故选:C.
4.B
【分析】分别计算三角函数值、零指数幂,化简绝对值,再进行加减即可.
【详解】解:
,
故选:B.
5.B
【分析】连接,,根据勾股定理可以得到,则是等腰三角形底边上的中线,根据三线合一定理,可以得到是直角三角形.根据三角函数的定义就可以求解.
【详解】如图,连接,,设正方形的网格边长是,则根据勾股定理可以得到:
,,
在中,由等腰三角形三线合一得:,
则,
,
故选:B.
6.B
【分析】根据特殊角的三角函数值即可求解.
【详解】解:∵,则,
故选:B.
7.C
【分析】根据特殊角的三角函数和三角板的特殊角的度数解答即可.
【详解】解:如图:
,
,
,
∴
故选:C.
8.B
【分析】根据代入求解即可得到答案.
【详解】解:由题意可得,
,
故选:B.
9.C
【分析】设点A的坐标为,过A点作轴,利用锐角三角函数和即可求出m,根据,设,根据点D经过反比例函数,即可求出n,进而求出答案.
【详解】解:设点A的坐标为,
过A点作轴,如图,
∵,,
∴,
∴,
∴,
,
,
或(舍),
∴,
∵四边形是菱形,,
∴,
设,
则,
∴,
∵点D经过反比例函数,
,
或(舍),
,
故选:C.
10.A
【分析】由是等边三角形和相似三角形的性质,得出,进而得到,再根据直角三角形的性质,得到,而,故①正确;根据等腰三角形的判定和性质以及三角形内角和定理,得出,可判定②正确;由,得,由与同高,可知,则判定③正确,由,得,则,可判定④正确.
【详解】解:为等边三角形,
,,
,
,
,
,
,
,,
,
在中,
,
,
又,
,
故①正确;
,,
,
,
故②正确;
,
,
,
又与同高,
,
又,,
,
,
故③正确;
,,
,
,
,
又,,
,
故④正确,
故选:A.
二、填空题
11.
【分析】利用特殊角的三角函数值得出,的值,进而得出答案.
【详解】解:在中,,,
,
则
.
故答案为:.
12.
【分析】根据特殊角的锐角三角函数值,即可求解.
【详解】解:∵,,
∴
则
故答案为:.
13.
【分析】代入特殊角的三角函数值,化简负整数指数幂,然后再计算.
【详解】解:原式
故答案为:
14.3
【分析】利用特殊角的三角函数值、二次根式的加法运算法则即可求解.
【详解】解:,
故答案为:3.
15.
【分析】先求出的余角,由即可求解.
【详解】解:由题意得
,
,
故答案:.
16.
【分析】连接,如图所示,由菱形性质及三角形中位线的判定与性质证得,,在中,.
【详解】解:连接,如图所示:
在菱形中,,点分别为的中点,
,
,
,
在菱形中,,点分别为的中点,
,
四边形是平行四边形,
,
,
,
,
在中,点分别为菱形的中点,
,
,
,
在中,点分别为菱形的中点,
,
,
在菱形中,,则,
在中,,,则,
故答案为:.
17.
【分析】过作于点,过作于点,即可得证,再根据相似三角形的性质得到和利用特殊角的正切值得出,然后设点的坐标为,继而根据反比例函数图像上点的特征得到,再次利用反比例函数图像上点的特征即可求得答案.
【详解】解:过作于点,过作于点,如图:
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴设点的坐标为,则,
∴,,
∴,
∵在反比例函数的图象上,
∴,
∵点在反比例函数的图象上,
∴.
故答案是:
18.
【分析】过点E作于点G,过点D作于点H,利用勾股定理,三角函数,特殊角的三角函数,三角形全等计算即可.
【详解】∵等边,
∴BC=CA=AB,∠BCD=∠CAE=∠ABC=600,
∵,
∴,
∴,,
∵∠BFE=∠DFC=∠CBD+∠BCF,
∴∠BFE=∠DFC=∠ACE+∠BCF=∠BCD=600,
过点E作于点G,
则,
设
则,,
∴,
∵,
∴,
解得,
∴,,
过点D作于点H,
则,
设
则,
∴,
解得,
∴,
∴,
故答案为:.
三、解答题
19.解:
.
20.解:原式,
,
.
21.解:
.
22.原式
,
∵
,
∴原式
.
23.解:
当时,
原式.
24.(1)∵
∴
∵
∴,
∴
∴
(2)∵由(1),
∴
∵
∴
∴
∵,
∴
∵
∴
∴
25.(1)①证明:∵四边形是正方形,
∴,.
∵,
∴,
∴;
②解:的大小不发生变化,;
理由:作,,垂足分别为点M、N,如图,
∵四边形是正方形,
∴,,
∴四边形是矩形,,
∴.
.∵,,
∴,
∴,
∴.
∴,即;
③解:
理由:作交于点E,作于点F,如图,
∵四边形是正方形,
∴,,
∴,四边形是矩形,
∴,,
∴,
∵,,
∴,
作于点M,
则,,
∴,
∵,,
∴,
∴;
(2)解:;
理由:四边形是菱形,,
∴,,,
∴是等边三角形,垂直平分,
∴,,
∵,
∴,
作交于点E,交于点G,如图,
则四边形是平行四边形,,,
∴,,都是等边三角形,
∴,
作于点M,
则,,
∴,
∴.
∵点位于中点,
∴
∴,
即
所以
26.(1)∵ 点,点,
∴,
∴,
∵ ,
∴,
∴是等边三角形,
∴,
∴.
(2)过点作轴于点D,过点作轴于点C,过点作轴于点F,
∴四边形是矩形,
∴,,
∵ 点,点,
∴,
∵ ,
∴,,,
∴,,,
∴,,
∴,
∴,
∴,
故点;.
(3)如图,根据旋转的性质,得到,
∴,
作点A关于x轴的对称点N,
连接交于点M,此时,有最小值,
∴点P与点M重合时,取得最小值,
∵ 点,
∴点,
设直线的解析式为,
∵点,点,
∴,
解得,
故直线的解析式为,
令,
得,
解得,
故点,
,
故的最小值为,此时点.
一、单选题
1.下列三角函数的值是的是( )
A. B. C. D.
2.在锐角中,若,则等于( )
A. B. C. D.
3.设,则下列式子成立的是( )
A. B.
C. D.
4.计算的值为( )
A. B. C. D.
5.正方形网格中,如图放置,则的值为( )
A. B. C.1 D.
6.在中,,,则( )
A. B. C. D.
7.三角板是我们数学学习中必不可少的工具,利用三角板可以拼出很多角,现将一副含45°角和30°角的三角板按如图所示的方式放置,则的值为( )
A. B. C. D.无法确定
8.的值等于( )
A.1 B. C. D.2
9.如图,在平面直角坐标系中,菱形的顶点为坐标原点,边在轴正半轴上,,反比例函数的图象经过点A,且交菱形对角线于点D,轴于点,则长为( )
A.1 B.3 C. D.
10.如图,在正方形中,是等边三角形,的延长线分别交于点、,连接,与相交于点.给出下列结论:①;②;③;④.其中正确的为( )
A.①②③④ B.①②③ C.②③④ D.①②④
二、填空题
11.在中,,,则的值为 .
12.锐角满足,则 度.
13.计算:.
14. .
15.若的余角是,则的值是 .
16.如图,在菱形中,.点分别为四边的中点,连接,则 .
17.如图,一块含有的直角三角板的直角顶点和坐标原点O重合,角的顶点A在反比例函数的图象上,顶点B在反比例函数的图象上,则k的值为 .
18.如图,等边中,点D在上,点E在上,,连接、交于点F,,,则的长为 .
三、解答题
19.计算:
20.计算:
21.计算:.
22.先化简,再求代数式的值,其中.
23.先化简,再求代数式的值,其中.
24.如图,已知,.
(1)求证:;
(2)若,,求.
25.(1)【问题探究】
如图1,在正方形中,对角线、相交于点.在线段上任取一点(端点除外),连接、.
①证明::
②将线段绕点逆时针旋转,使点落在的延长线上的点处.当点在线段上的位置发生变化时,的大小是否发生变化?请说明理由;
③探究与的数量关系为______.
(2)【迁移探究】
如图2,将正方形换成菱形,且,点位于中点,其他条件不变.探究与的数量关系为______.
26.在平面直角坐标系中,O为原点,点,点,把绕点A逆时针旋转,得,点B,O旋转后的对应点为,,记旋转角为α.
(1)如图1,若,连接,求的长度;
(2)如图2,若,求的坐标并直接写出的坐标;
(3)在(2)的条件下,边上的一点P旋转后的对应点为,请直接写出的最小值和此时点P的坐标.
答案
一、单选题
1.A
【分析】根据特殊角的三角函数值解答.
【详解】解:,,, ,
观察四个选项,选项A符合题意,
故选:A.
2.A
【分析】根据平方及绝对值的非负性可得,,由特殊角的三角函数值求得和,再由三角形内角和为即可解答;
【详解】解:∵,
∴,,
∴,,
∴在锐角中,,
故选: A;
3.C
【分析】根据的取值范围选择特殊值,然后求出正弦、余弦、正切的值,进行比较即可得到答案.
【详解】解:,
取,
,,,
,
,
故选:C.
4.B
【分析】分别计算三角函数值、零指数幂,化简绝对值,再进行加减即可.
【详解】解:
,
故选:B.
5.B
【分析】连接,,根据勾股定理可以得到,则是等腰三角形底边上的中线,根据三线合一定理,可以得到是直角三角形.根据三角函数的定义就可以求解.
【详解】如图,连接,,设正方形的网格边长是,则根据勾股定理可以得到:
,,
在中,由等腰三角形三线合一得:,
则,
,
故选:B.
6.B
【分析】根据特殊角的三角函数值即可求解.
【详解】解:∵,则,
故选:B.
7.C
【分析】根据特殊角的三角函数和三角板的特殊角的度数解答即可.
【详解】解:如图:
,
,
,
∴
故选:C.
8.B
【分析】根据代入求解即可得到答案.
【详解】解:由题意可得,
,
故选:B.
9.C
【分析】设点A的坐标为,过A点作轴,利用锐角三角函数和即可求出m,根据,设,根据点D经过反比例函数,即可求出n,进而求出答案.
【详解】解:设点A的坐标为,
过A点作轴,如图,
∵,,
∴,
∴,
∴,
,
,
或(舍),
∴,
∵四边形是菱形,,
∴,
设,
则,
∴,
∵点D经过反比例函数,
,
或(舍),
,
故选:C.
10.A
【分析】由是等边三角形和相似三角形的性质,得出,进而得到,再根据直角三角形的性质,得到,而,故①正确;根据等腰三角形的判定和性质以及三角形内角和定理,得出,可判定②正确;由,得,由与同高,可知,则判定③正确,由,得,则,可判定④正确.
【详解】解:为等边三角形,
,,
,
,
,
,
,
,,
,
在中,
,
,
又,
,
故①正确;
,,
,
,
故②正确;
,
,
,
又与同高,
,
又,,
,
,
故③正确;
,,
,
,
,
又,,
,
故④正确,
故选:A.
二、填空题
11.
【分析】利用特殊角的三角函数值得出,的值,进而得出答案.
【详解】解:在中,,,
,
则
.
故答案为:.
12.
【分析】根据特殊角的锐角三角函数值,即可求解.
【详解】解:∵,,
∴
则
故答案为:.
13.
【分析】代入特殊角的三角函数值,化简负整数指数幂,然后再计算.
【详解】解:原式
故答案为:
14.3
【分析】利用特殊角的三角函数值、二次根式的加法运算法则即可求解.
【详解】解:,
故答案为:3.
15.
【分析】先求出的余角,由即可求解.
【详解】解:由题意得
,
,
故答案:.
16.
【分析】连接,如图所示,由菱形性质及三角形中位线的判定与性质证得,,在中,.
【详解】解:连接,如图所示:
在菱形中,,点分别为的中点,
,
,
,
在菱形中,,点分别为的中点,
,
四边形是平行四边形,
,
,
,
,
在中,点分别为菱形的中点,
,
,
,
在中,点分别为菱形的中点,
,
,
在菱形中,,则,
在中,,,则,
故答案为:.
17.
【分析】过作于点,过作于点,即可得证,再根据相似三角形的性质得到和利用特殊角的正切值得出,然后设点的坐标为,继而根据反比例函数图像上点的特征得到,再次利用反比例函数图像上点的特征即可求得答案.
【详解】解:过作于点,过作于点,如图:
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴设点的坐标为,则,
∴,,
∴,
∵在反比例函数的图象上,
∴,
∵点在反比例函数的图象上,
∴.
故答案是:
18.
【分析】过点E作于点G,过点D作于点H,利用勾股定理,三角函数,特殊角的三角函数,三角形全等计算即可.
【详解】∵等边,
∴BC=CA=AB,∠BCD=∠CAE=∠ABC=600,
∵,
∴,
∴,,
∵∠BFE=∠DFC=∠CBD+∠BCF,
∴∠BFE=∠DFC=∠ACE+∠BCF=∠BCD=600,
过点E作于点G,
则,
设
则,,
∴,
∵,
∴,
解得,
∴,,
过点D作于点H,
则,
设
则,
∴,
解得,
∴,
∴,
故答案为:.
三、解答题
19.解:
.
20.解:原式,
,
.
21.解:
.
22.原式
,
∵
,
∴原式
.
23.解:
当时,
原式.
24.(1)∵
∴
∵
∴,
∴
∴
(2)∵由(1),
∴
∵
∴
∴
∵,
∴
∵
∴
∴
25.(1)①证明:∵四边形是正方形,
∴,.
∵,
∴,
∴;
②解:的大小不发生变化,;
理由:作,,垂足分别为点M、N,如图,
∵四边形是正方形,
∴,,
∴四边形是矩形,,
∴.
.∵,,
∴,
∴,
∴.
∴,即;
③解:
理由:作交于点E,作于点F,如图,
∵四边形是正方形,
∴,,
∴,四边形是矩形,
∴,,
∴,
∵,,
∴,
作于点M,
则,,
∴,
∵,,
∴,
∴;
(2)解:;
理由:四边形是菱形,,
∴,,,
∴是等边三角形,垂直平分,
∴,,
∵,
∴,
作交于点E,交于点G,如图,
则四边形是平行四边形,,,
∴,,都是等边三角形,
∴,
作于点M,
则,,
∴,
∴.
∵点位于中点,
∴
∴,
即
所以
26.(1)∵ 点,点,
∴,
∴,
∵ ,
∴,
∴是等边三角形,
∴,
∴.
(2)过点作轴于点D,过点作轴于点C,过点作轴于点F,
∴四边形是矩形,
∴,,
∵ 点,点,
∴,
∵ ,
∴,,,
∴,,,
∴,,
∴,
∴,
∴,
故点;.
(3)如图,根据旋转的性质,得到,
∴,
作点A关于x轴的对称点N,
连接交于点M,此时,有最小值,
∴点P与点M重合时,取得最小值,
∵ 点,
∴点,
设直线的解析式为,
∵点,点,
∴,
解得,
故直线的解析式为,
令,
得,
解得,
故点,
,
故的最小值为,此时点.
