苏科版七年级数学下册 第八章 整式乘法 单元测试题(2024)(含解析)
文档属性
| 名称 | 苏科版七年级数学下册 第八章 整式乘法 单元测试题(2024)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 206.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 13:14:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏科版七年级数学下册 第八章 整式乘法 单元测试题(2024)
一、选择题(共10题;共30分)
1.(3分)计算的结果是( )
A. B. C. D.
2.(3分)一个长方体,它的底面是边长为的正方形,高为,它的体积是( )
A. B. C. D.
3.(3分) 化简的结果正确的是( )
A. B. C. D.
4.(3分) 某天, 小丽拿出课堂笔记准备复习时, 发现有一道题 , 不小心被一滴墨水覆盖了 ( 处), 那么被覆盖的一项是( )
A. B. C. D.
5.(3分)若,则m的值为( )
A. B.6 C.2 D.
6.(3分)计算,所得结果的一次项系数是( )
A.-2 B.-1 C.1 D.2
7.(3分)如图,从边长为a的正方形中去掉一个边长为1的小正方形,然后将剩余部分剪后拼成一个长方形,上述操作能验证的等式是( )
A. B.
C. D.
8.(3分)若,那么k的值是( )
A.5 B. C.10 D.
9.(3分)今天数学课上,老师讲了单项式乘以多项式,放学回到家,小明拿出课堂笔记复习,发现一道题: , 的地方被钢笔水弄污了,你认为 内上应填写
A.3xy B. C. D.1
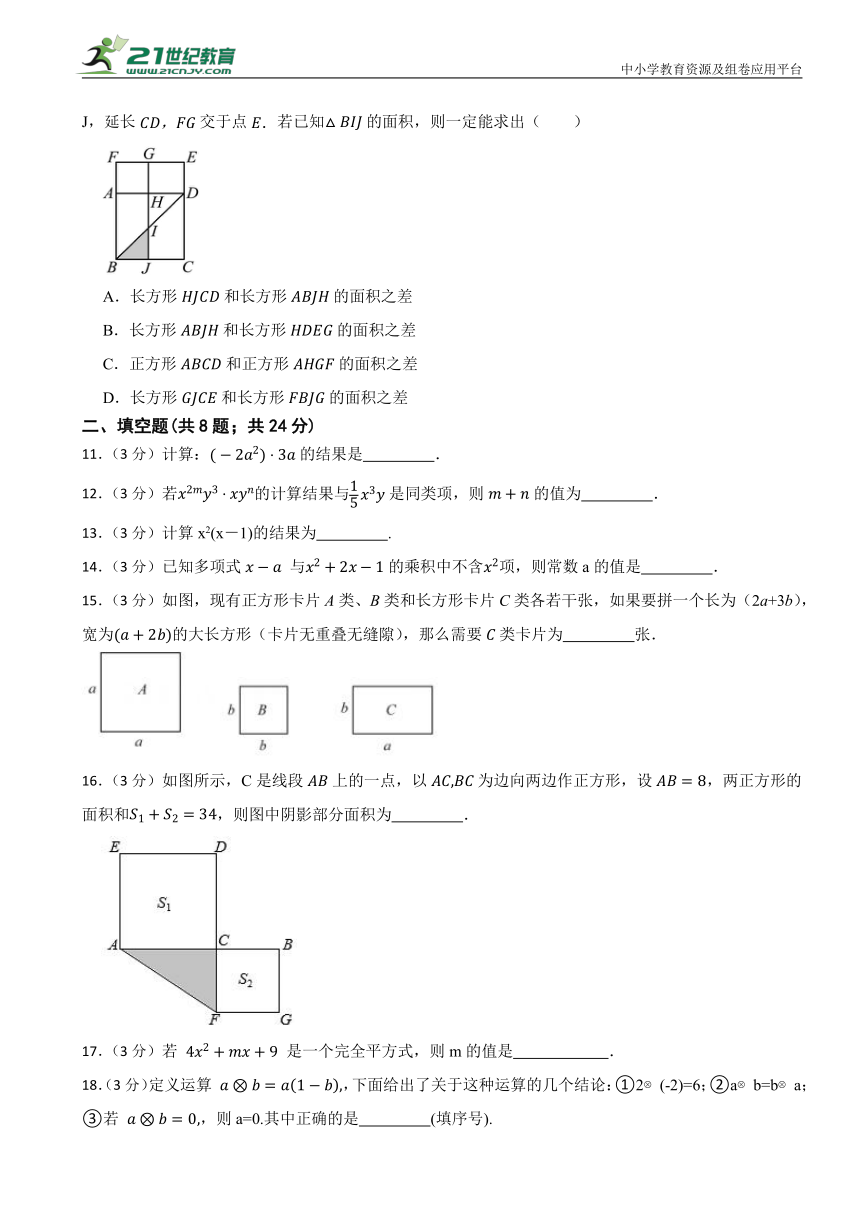
10.(3分)如图,四边形和四边形均为正方形,连接,延长分别交于点I,J,延长交于点若已知的面积,则一定能求出( )
A.长方形和长方形的面积之差
B.长方形和长方形的面积之差
C.正方形和正方形的面积之差
D.长方形和长方形的面积之差
二、填空题(共8题;共24分)
11.(3分)计算:的结果是 .
12.(3分)若的计算结果与是同类项,则的值为 .
13.(3分)计算x2(x-1)的结果为 .
14.(3分)已知多项式 与的乘积中不含项,则常数a的值是 .
15.(3分)如图,现有正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(2a+3b),宽为的大长方形(卡片无重叠无缝隙),那么需要类卡片为 张.
16.(3分)如图所示,C是线段上的一点,以为边向两边作正方形,设,两正方形的面积和,则图中阴影部分面积为 .
17.(3分)若 是一个完全平方式,则m的值是 .
18.(3分)定义运算 ,下面给出了关于这种运算的几个结论:①2 (-2)=6;②a b=b a;③若 ,则a=0.其中正确的是 (填序号).
三、解答题(共8题;共66分)
19.(8分)计算:
(1)(4分);
(2)(4分).
20.(6分)当,时,求代数式的值.
21.(6分)小明在计算 时,解答过程如下:
a(2+a)-(a-2)2
=2a+a2-(a2-4)…第一步
=2a+a2-a2-4…第二步
=2a-4…第三步
小明的解答从第 ________步开始出错,请写出正确的解答过程.
22.(8分)先化简,再求值:,其中.
23.(8分)一块长方形硬纸片,长为(5a2+4b2)m,宽为6a4m,在它的四个角上分别剪去一个边长为 m的小正方形,然后折成一个无盖的盒子,请你求这个无盖盒子的表面积.
24.(8分)在莹莹住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为米,宽为米的长方形草坪上修建一横一竖互相垂直且宽度均为a米的通道.
(1)(4分)用含a、b的式子表示剩余草坪的面积;
(2)(4分)若,,求剩余草坪的面积.
25.(10分)对于任何数,我们规定:例如:.
(1)(4分)按照这个规定,请你化简;
(2)(6分)按照这个规定,请你计算:当时,求的值.
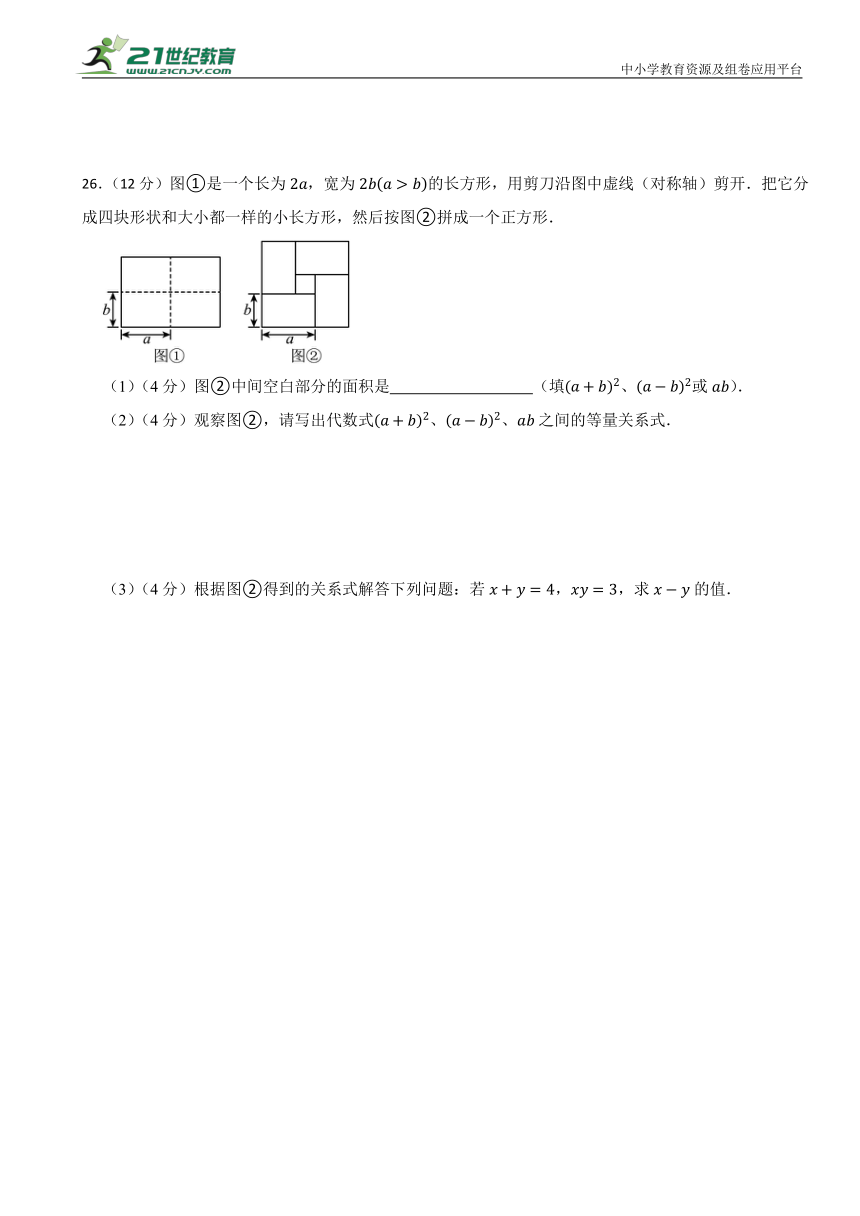
26.(12分)图①是一个长为,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开.把它分成四块形状和大小都一样的小长方形,然后按图②拼成一个正方形.
(1)(4分)图②中间空白部分的面积是 (填、或).
(2)(4分)观察图②,请写出代数式、、之间的等量关系式.
(3)(4分)根据图②得到的关系式解答下列问题:若,,求的值.
答案解析部分
1.【答案】D
【知识点】单项式乘单项式
【解析】【解答】解:
,
故答案为:D.
【分析】利用单项式乘以单项式的法则“单项式乘以单项式,把系数与相同字母的幂分别相乘,对于只在某一个单项式含有的字母,则连同指数作为积的一个因式”计算即可.
2.【答案】D
【知识点】单项式乘单项式
【解析】【解答】解: 长方体的体积为··= ;
故答案为:D.
【分析】 长方体的体积=长×宽×高,据此计算即可.
3.【答案】B
【知识点】单项式乘多项式
【解析】【解答】解:
故答案为:B.
【分析】根据单项式乘以多项式法则“单项式乘以多项式,就是用单项式去乘以多项式的每一项,再把所得的积相加”计算即可求解.
4.【答案】B
【知识点】单项式乘多项式
【解析】【解答】解:
∴,
故答案为:B.
【分析】根据单项式乘多项式展开,逐一对应即可.
5.【答案】C
【知识点】多项式乘多项式
【解析】【解答】解:根据题意得,
∵
∴m=2.
故答案为:C.
【分析】根据多项式乘多项式的运算法则将计算出来,然后根据,即可求出m的值.
6.【答案】A
【知识点】多项式乘多项式;多项式的项、系数与次数
【解析】【解答】解:=x3-2x+x2-2,
∴所得结果的一次项系数为-2.
故答案为:A.
【分析】利用多项式乘多项式法则进行计算,再求解即可.
7.【答案】A
【知识点】平方差公式的几何背景
【解析】【解答】解:由图可知,两个阴影部分的面积和,也可以用来表示;
∴能验证的等式是;
故答案为:A.
【分析】根据两个阴影部分的面积和可以用两个正方形的面积差表示,也可以用长方形的面积公式进行表示,即可得出结论.
8.【答案】D
【知识点】完全平方公式及运用
【解析】【解答】解:∵,且,
∴k=-10.
故答案为:D
【分析】利用完全平方公式解答即可.
9.【答案】A
【知识点】单项式乘多项式
【解析】【解答】解:-3xy(4y-2x-1)=-12xy2+6x2y+3xy
∴缺少的一项为3xy
故答案为:A.
【分析】根据题意,将等号左侧的式子进行运算,得到的结果与右边比对,即可得到答案。
10.【答案】B
【知识点】多项式乘多项式
【解析】【解答】解:四边形是正方形,
,
阴影三角形是等腰直角三角形,
阴影部分的面积等于正方形的一半,
设正方形的边长为a,正方形的边长为b,则正方形的面积为,
长方形的长为a,宽为b,因此面积为,
长方形的长为,宽为b,因此面积为,
,
故答案为:B.
【分析】设正方形和的边长为a和b,表示图形中各个部分的面积,然后逐项判断即可解题.
11.【答案】
【知识点】单项式乘单项式
【解析】【解答】解:;
故答案是:
【分析】根据单项式乘单项式的运算法则进行计算即可.
12.【答案】
【知识点】同底数幂的乘法;单项式乘单项式;同类项的概念;求代数式的值-直接代入求值
【解析】【解答】解:由,
∵的计算结果与是同类项,
∴,,
解得,,
∴,
故答案为:.
【分析】本题考查了同底数幂的乘法,以及同类项的定义,根据题意,得到,由同类项的定义,得到,,求得的值,将的值代入代数式 ,进行计算,即可求解.
13.【答案】x3-x2
【知识点】单项式乘多项式
【解析】【解答】解:x2(x-1)=x3-x2.
故答案为:x3-x2.
【分析】直接利用单项式乘多项式运算法则计算得出答案.
14.【答案】2
【知识点】多项式乘多项式;多项式的项、系数与次数
【解析】【解答】解:∵
又∵多项式 与的乘积中不含项,
∴
∴
故答案为:2.
【分析】根据多项式乘以多项式的计算法则求出两个多项式的积为然后根据题意得到据此即可求出a的值.
15.【答案】7
【知识点】多项式乘多项式
【解析】【解答】解:由题可得A类卡片的面积为a2,
B类卡片的面积为b2,
C类卡片的面积为ab,
大卡片的面积为(2a+3b)(a+2b)=2a2+7ab+6b2,
ab的系数为7,
只需要C类卡片7张,
故答案为:7.
【分析】分别求出三类卡片的面积,从而得到大卡片的总面积,对比各项系数,进而求解.
16.【答案】
【知识点】完全平方公式的几何背景
【解析】【解答】解:AC=a,BC=CF=b,
则a+b=8,a2+b2=34,
∴a2+b2=(a+b)2-2ab,
即34=64-2ab,
∴ab=15,
∴S阴影=ab=,
故答案为:.
【分析】设AC=a,BC=b,即可得到a+b=8,a2+b2=34,根据完全平方公式的变形求出ab即可解题.
17.【答案】12或-12
【知识点】完全平方公式及运用
【解析】【解答】解:根据题意得,
或 ,
故答案为:12或-12.
【分析】根据完全平方式 的形式即可求出m的值.
18.【答案】①
【知识点】整式的混合运算
【解析】【解答】解:①2 (﹣2)
=2×[1﹣(﹣2)]
=2×3
=6,
故本选项正确;
②a b
=a×(1﹣b)
=a﹣ab
b a
=b(1﹣a)
=b﹣ab,
故本选项错误;
③∵a b=a(1﹣b)=0,
∴a=0错误.
故本选项错误.
故答案为:①.
【分析】本题需先根据a b=a(1﹣b)的运算法则,分别对每一项进行计算得出正确结果,最后判断出所选的结论.
19.【答案】(1)解:
;
(2)解:
.
【知识点】同底数幂的乘法;多项式乘多项式;积的乘方运算;幂的乘方运算
【解析】【分析】(1)根据整式的运算法则,先进行幂的运算,再合并同类项,进行加减运算,即可解答;
(2)根据多项式与多项式的乘法法则, 多项式与多项式相乘:先用一个多项式的每一项分别乘以另一个多项式每一项,再把所得的积相加,其中多项式乘以多项式就是利用乘法分配律进行计算,即可解答.
(1)解:
;
(2)解:
.
20.【答案】解:,
∴当,时,
原式.
【知识点】完全平方公式及运用;求代数式的值-直接代入求值
【解析】【分析】本题考查了完全平方公式逆运算,根据完全平方公式对代数式变形,再代值求解,即可得到答案.
21.【答案】解:小明的解答从第一步开始出错,正确解答过程如下:
【知识点】整式的混合运算
【解析】【分析】利用完全平方公式将括号里的算式进行化简,然后去括号合并同类项即可.
22.【答案】解:原式,
,
当时,
原式,
=4+12,
=16.
【知识点】单项式乘多项式;完全平方公式及运用;平方差公式及应用
【解析】【分析】先根据完全平方公式、平方差公式、单项式乘多项式将所求多项式展开,再合并同类项,然后代入x,y的值进行计算即可.
23.【答案】解:纸片的面积是:(5a2+4b2) 6a4=30a6+24a4b2;
小正方形的面积是:( a3)2= a6,
则无盖盒子的表面积是:30a6+24a4b2﹣4× a6=21a6+24a4b2
【知识点】单项式乘多项式
【解析】【分析】利用纸片的面积减去剪去的4个小正方形的面积就是盒子的表面积.
24.【答案】(1)解:由题意得剩余草坪的面积为
答:剩余草坪的面积为平方米.
(2)解:当,时,原式,
∴剩余草坪的面积是260平方米.
【知识点】多项式乘多项式;用代数式表示几何图形的数量关系;求代数式的值-直接代入求值
【解析】【分析】(1)根据题意用代数式表示剩余草坪的面积,进而即可求解;
(2)将a和b的值代入代数式,进而即可求解。
(1)解:依题意,剩余草坪的面积为
答:剩余草坪的面积为平方米.
(2)当,时,原式,
∴剩余草坪的面积是260平方米.
25.【答案】(1)由题意得:
(2)由题意得:
,
,
,
原式.
【知识点】多项式乘多项式
【解析】【分析】(1)直接由题意定义的计算规则求值即可;
(2)由定义的计算规则化简整体代入求值即可.
26.【答案】(1)
(2)解:由图②可知:大正方形面积=空白部分的面积+4个长方形面积,
∴;
(3)解:∵,
∴,
∵,,
∴,
∴.
.
【知识点】完全平方公式的几何背景
【解析】【解答】解:(1)由图形可知:空白部分的面积.
故答案为:;
【分析】(1)根据题意得到空白部分的面积=大正方形的面积-4个小长方形面积,进而计算即可得到代数式;
(2)根据图②得到大正方形面积=空白部分的面积+4个长方形面积,进而根据整式的混合运算即可求解;
(3)由(2)可得:,进而根据整式的混合运算进行计算即可求解。
(1)解:由图形可知:空白部分的面积.
故答案为:;
(2)解:由图②可知:大正方形面积=空白部分的面积+4个长方形面积,
∴;
(3)解:∵,
∴,
∵,,
∴,
∴.
苏科版七年级数学下册 第八章 整式乘法 单元测试题(2024)
一、选择题(共10题;共30分)
1.(3分)计算的结果是( )
A. B. C. D.
2.(3分)一个长方体,它的底面是边长为的正方形,高为,它的体积是( )
A. B. C. D.
3.(3分) 化简的结果正确的是( )
A. B. C. D.
4.(3分) 某天, 小丽拿出课堂笔记准备复习时, 发现有一道题 , 不小心被一滴墨水覆盖了 ( 处), 那么被覆盖的一项是( )
A. B. C. D.
5.(3分)若,则m的值为( )
A. B.6 C.2 D.
6.(3分)计算,所得结果的一次项系数是( )
A.-2 B.-1 C.1 D.2
7.(3分)如图,从边长为a的正方形中去掉一个边长为1的小正方形,然后将剩余部分剪后拼成一个长方形,上述操作能验证的等式是( )
A. B.
C. D.
8.(3分)若,那么k的值是( )
A.5 B. C.10 D.
9.(3分)今天数学课上,老师讲了单项式乘以多项式,放学回到家,小明拿出课堂笔记复习,发现一道题: , 的地方被钢笔水弄污了,你认为 内上应填写
A.3xy B. C. D.1
10.(3分)如图,四边形和四边形均为正方形,连接,延长分别交于点I,J,延长交于点若已知的面积,则一定能求出( )
A.长方形和长方形的面积之差
B.长方形和长方形的面积之差
C.正方形和正方形的面积之差
D.长方形和长方形的面积之差
二、填空题(共8题;共24分)
11.(3分)计算:的结果是 .
12.(3分)若的计算结果与是同类项,则的值为 .
13.(3分)计算x2(x-1)的结果为 .
14.(3分)已知多项式 与的乘积中不含项,则常数a的值是 .
15.(3分)如图,现有正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(2a+3b),宽为的大长方形(卡片无重叠无缝隙),那么需要类卡片为 张.
16.(3分)如图所示,C是线段上的一点,以为边向两边作正方形,设,两正方形的面积和,则图中阴影部分面积为 .
17.(3分)若 是一个完全平方式,则m的值是 .
18.(3分)定义运算 ,下面给出了关于这种运算的几个结论:①2 (-2)=6;②a b=b a;③若 ,则a=0.其中正确的是 (填序号).
三、解答题(共8题;共66分)
19.(8分)计算:
(1)(4分);
(2)(4分).
20.(6分)当,时,求代数式的值.
21.(6分)小明在计算 时,解答过程如下:
a(2+a)-(a-2)2
=2a+a2-(a2-4)…第一步
=2a+a2-a2-4…第二步
=2a-4…第三步
小明的解答从第 ________步开始出错,请写出正确的解答过程.
22.(8分)先化简,再求值:,其中.
23.(8分)一块长方形硬纸片,长为(5a2+4b2)m,宽为6a4m,在它的四个角上分别剪去一个边长为 m的小正方形,然后折成一个无盖的盒子,请你求这个无盖盒子的表面积.
24.(8分)在莹莹住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为米,宽为米的长方形草坪上修建一横一竖互相垂直且宽度均为a米的通道.
(1)(4分)用含a、b的式子表示剩余草坪的面积;
(2)(4分)若,,求剩余草坪的面积.
25.(10分)对于任何数,我们规定:例如:.
(1)(4分)按照这个规定,请你化简;
(2)(6分)按照这个规定,请你计算:当时,求的值.
26.(12分)图①是一个长为,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开.把它分成四块形状和大小都一样的小长方形,然后按图②拼成一个正方形.
(1)(4分)图②中间空白部分的面积是 (填、或).
(2)(4分)观察图②,请写出代数式、、之间的等量关系式.
(3)(4分)根据图②得到的关系式解答下列问题:若,,求的值.
答案解析部分
1.【答案】D
【知识点】单项式乘单项式
【解析】【解答】解:
,
故答案为:D.
【分析】利用单项式乘以单项式的法则“单项式乘以单项式,把系数与相同字母的幂分别相乘,对于只在某一个单项式含有的字母,则连同指数作为积的一个因式”计算即可.
2.【答案】D
【知识点】单项式乘单项式
【解析】【解答】解: 长方体的体积为··= ;
故答案为:D.
【分析】 长方体的体积=长×宽×高,据此计算即可.
3.【答案】B
【知识点】单项式乘多项式
【解析】【解答】解:
故答案为:B.
【分析】根据单项式乘以多项式法则“单项式乘以多项式,就是用单项式去乘以多项式的每一项,再把所得的积相加”计算即可求解.
4.【答案】B
【知识点】单项式乘多项式
【解析】【解答】解:
∴,
故答案为:B.
【分析】根据单项式乘多项式展开,逐一对应即可.
5.【答案】C
【知识点】多项式乘多项式
【解析】【解答】解:根据题意得,
∵
∴m=2.
故答案为:C.
【分析】根据多项式乘多项式的运算法则将计算出来,然后根据,即可求出m的值.
6.【答案】A
【知识点】多项式乘多项式;多项式的项、系数与次数
【解析】【解答】解:=x3-2x+x2-2,
∴所得结果的一次项系数为-2.
故答案为:A.
【分析】利用多项式乘多项式法则进行计算,再求解即可.
7.【答案】A
【知识点】平方差公式的几何背景
【解析】【解答】解:由图可知,两个阴影部分的面积和,也可以用来表示;
∴能验证的等式是;
故答案为:A.
【分析】根据两个阴影部分的面积和可以用两个正方形的面积差表示,也可以用长方形的面积公式进行表示,即可得出结论.
8.【答案】D
【知识点】完全平方公式及运用
【解析】【解答】解:∵,且,
∴k=-10.
故答案为:D
【分析】利用完全平方公式解答即可.
9.【答案】A
【知识点】单项式乘多项式
【解析】【解答】解:-3xy(4y-2x-1)=-12xy2+6x2y+3xy
∴缺少的一项为3xy
故答案为:A.
【分析】根据题意,将等号左侧的式子进行运算,得到的结果与右边比对,即可得到答案。
10.【答案】B
【知识点】多项式乘多项式
【解析】【解答】解:四边形是正方形,
,
阴影三角形是等腰直角三角形,
阴影部分的面积等于正方形的一半,
设正方形的边长为a,正方形的边长为b,则正方形的面积为,
长方形的长为a,宽为b,因此面积为,
长方形的长为,宽为b,因此面积为,
,
故答案为:B.
【分析】设正方形和的边长为a和b,表示图形中各个部分的面积,然后逐项判断即可解题.
11.【答案】
【知识点】单项式乘单项式
【解析】【解答】解:;
故答案是:
【分析】根据单项式乘单项式的运算法则进行计算即可.
12.【答案】
【知识点】同底数幂的乘法;单项式乘单项式;同类项的概念;求代数式的值-直接代入求值
【解析】【解答】解:由,
∵的计算结果与是同类项,
∴,,
解得,,
∴,
故答案为:.
【分析】本题考查了同底数幂的乘法,以及同类项的定义,根据题意,得到,由同类项的定义,得到,,求得的值,将的值代入代数式 ,进行计算,即可求解.
13.【答案】x3-x2
【知识点】单项式乘多项式
【解析】【解答】解:x2(x-1)=x3-x2.
故答案为:x3-x2.
【分析】直接利用单项式乘多项式运算法则计算得出答案.
14.【答案】2
【知识点】多项式乘多项式;多项式的项、系数与次数
【解析】【解答】解:∵
又∵多项式 与的乘积中不含项,
∴
∴
故答案为:2.
【分析】根据多项式乘以多项式的计算法则求出两个多项式的积为然后根据题意得到据此即可求出a的值.
15.【答案】7
【知识点】多项式乘多项式
【解析】【解答】解:由题可得A类卡片的面积为a2,
B类卡片的面积为b2,
C类卡片的面积为ab,
大卡片的面积为(2a+3b)(a+2b)=2a2+7ab+6b2,
ab的系数为7,
只需要C类卡片7张,
故答案为:7.
【分析】分别求出三类卡片的面积,从而得到大卡片的总面积,对比各项系数,进而求解.
16.【答案】
【知识点】完全平方公式的几何背景
【解析】【解答】解:AC=a,BC=CF=b,
则a+b=8,a2+b2=34,
∴a2+b2=(a+b)2-2ab,
即34=64-2ab,
∴ab=15,
∴S阴影=ab=,
故答案为:.
【分析】设AC=a,BC=b,即可得到a+b=8,a2+b2=34,根据完全平方公式的变形求出ab即可解题.
17.【答案】12或-12
【知识点】完全平方公式及运用
【解析】【解答】解:根据题意得,
或 ,
故答案为:12或-12.
【分析】根据完全平方式 的形式即可求出m的值.
18.【答案】①
【知识点】整式的混合运算
【解析】【解答】解:①2 (﹣2)
=2×[1﹣(﹣2)]
=2×3
=6,
故本选项正确;
②a b
=a×(1﹣b)
=a﹣ab
b a
=b(1﹣a)
=b﹣ab,
故本选项错误;
③∵a b=a(1﹣b)=0,
∴a=0错误.
故本选项错误.
故答案为:①.
【分析】本题需先根据a b=a(1﹣b)的运算法则,分别对每一项进行计算得出正确结果,最后判断出所选的结论.
19.【答案】(1)解:
;
(2)解:
.
【知识点】同底数幂的乘法;多项式乘多项式;积的乘方运算;幂的乘方运算
【解析】【分析】(1)根据整式的运算法则,先进行幂的运算,再合并同类项,进行加减运算,即可解答;
(2)根据多项式与多项式的乘法法则, 多项式与多项式相乘:先用一个多项式的每一项分别乘以另一个多项式每一项,再把所得的积相加,其中多项式乘以多项式就是利用乘法分配律进行计算,即可解答.
(1)解:
;
(2)解:
.
20.【答案】解:,
∴当,时,
原式.
【知识点】完全平方公式及运用;求代数式的值-直接代入求值
【解析】【分析】本题考查了完全平方公式逆运算,根据完全平方公式对代数式变形,再代值求解,即可得到答案.
21.【答案】解:小明的解答从第一步开始出错,正确解答过程如下:
【知识点】整式的混合运算
【解析】【分析】利用完全平方公式将括号里的算式进行化简,然后去括号合并同类项即可.
22.【答案】解:原式,
,
当时,
原式,
=4+12,
=16.
【知识点】单项式乘多项式;完全平方公式及运用;平方差公式及应用
【解析】【分析】先根据完全平方公式、平方差公式、单项式乘多项式将所求多项式展开,再合并同类项,然后代入x,y的值进行计算即可.
23.【答案】解:纸片的面积是:(5a2+4b2) 6a4=30a6+24a4b2;
小正方形的面积是:( a3)2= a6,
则无盖盒子的表面积是:30a6+24a4b2﹣4× a6=21a6+24a4b2
【知识点】单项式乘多项式
【解析】【分析】利用纸片的面积减去剪去的4个小正方形的面积就是盒子的表面积.
24.【答案】(1)解:由题意得剩余草坪的面积为
答:剩余草坪的面积为平方米.
(2)解:当,时,原式,
∴剩余草坪的面积是260平方米.
【知识点】多项式乘多项式;用代数式表示几何图形的数量关系;求代数式的值-直接代入求值
【解析】【分析】(1)根据题意用代数式表示剩余草坪的面积,进而即可求解;
(2)将a和b的值代入代数式,进而即可求解。
(1)解:依题意,剩余草坪的面积为
答:剩余草坪的面积为平方米.
(2)当,时,原式,
∴剩余草坪的面积是260平方米.
25.【答案】(1)由题意得:
(2)由题意得:
,
,
,
原式.
【知识点】多项式乘多项式
【解析】【分析】(1)直接由题意定义的计算规则求值即可;
(2)由定义的计算规则化简整体代入求值即可.
26.【答案】(1)
(2)解:由图②可知:大正方形面积=空白部分的面积+4个长方形面积,
∴;
(3)解:∵,
∴,
∵,,
∴,
∴.
.
【知识点】完全平方公式的几何背景
【解析】【解答】解:(1)由图形可知:空白部分的面积.
故答案为:;
【分析】(1)根据题意得到空白部分的面积=大正方形的面积-4个小长方形面积,进而计算即可得到代数式;
(2)根据图②得到大正方形面积=空白部分的面积+4个长方形面积,进而根据整式的混合运算即可求解;
(3)由(2)可得:,进而根据整式的混合运算进行计算即可求解。
(1)解:由图形可知:空白部分的面积.
故答案为:;
(2)解:由图②可知:大正方形面积=空白部分的面积+4个长方形面积,
∴;
(3)解:∵,
∴,
∵,,
∴,
∴.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
