华师大版七年级数学下册 第六章 一次方程组 单元测试题(2024)(含解析)
文档属性
| 名称 | 华师大版七年级数学下册 第六章 一次方程组 单元测试题(2024)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 15:53:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
华师大版七年级数学下册 第六章 一次方程组 单元测试题(2024)
一、选择题(共10题;共30分)
1.(3分)若是关于x和y的二元一次方程的解,则a的值是( )
A.3 B.4 C. D.
2.(3分)方程组的解为,则被●和▲遮盖的两个数分别为( )
A.5,1 B.1,3 C.2,3 D.2,4
3.(3分)我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )
A. B. C. D.
4.(3分)方程组 的解是 ( ).
A. B. C. D.
5.(3分)用加减消元法解方程组,下列做法正确的是( )
A. B. C. D.
6.(3分)已知 且 , 则 的值( )
A.为 9 B.为 -3 C.为 12 D.不确定
7.(3分)解三元一次方程组 , 时, 最简单的做法是( )
A.先消去 B.先消去 C.先消去 D.先消去常数
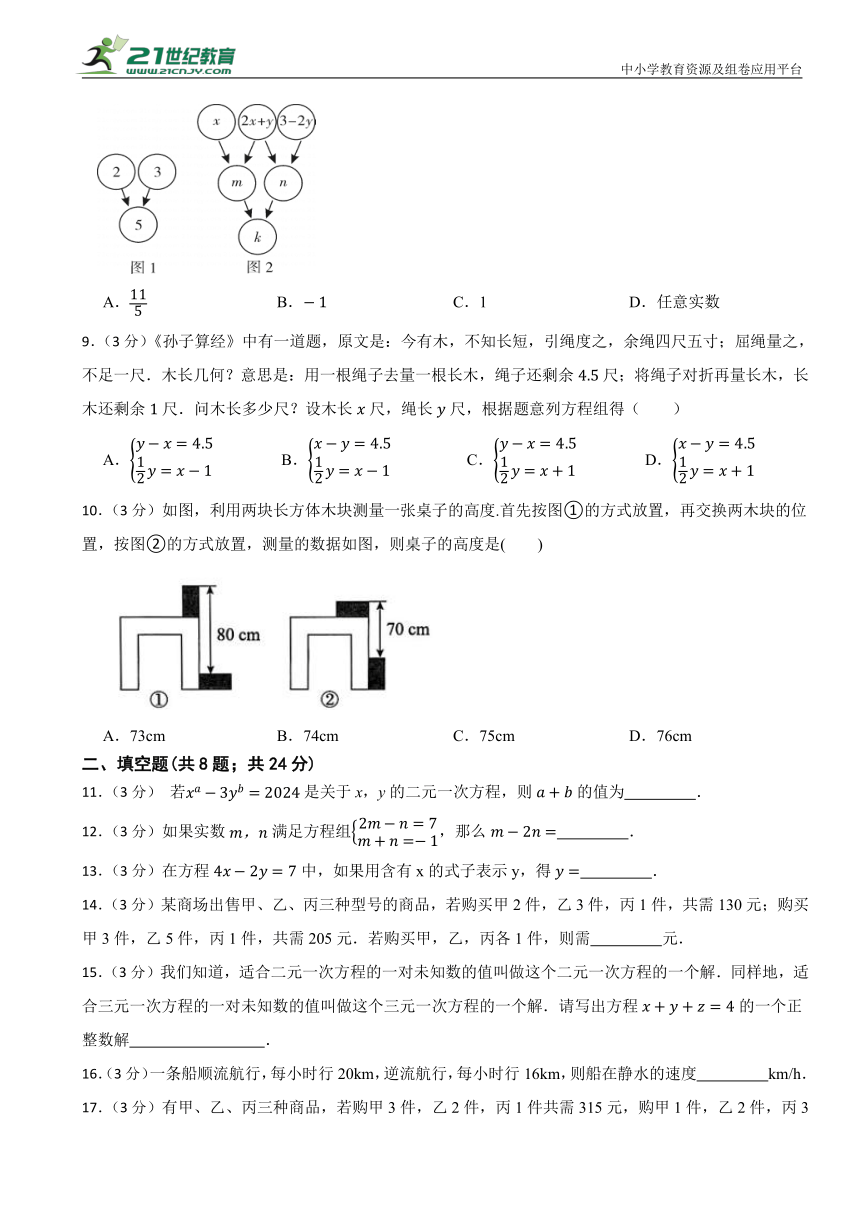
8.(3分)我们约定:上方相邻两数之和等于这两数下方箭头共同指向的数,如图1,有,在图2中,若的值为8,则的值为( )
A. B. C.1 D.任意实数
9.(3分)《孙子算经》中有一道题,原文是:今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?意思是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺.问木长多少尺?设木长尺,绳长尺,根据题意列方程组得( )
A. B. C. D.
10.(3分)如图,利用两块长方体木块测量一张桌子的高度.首先按图①的方式放置,再交换两木块的位置,按图②的方式放置,测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
二、填空题(共8题;共24分)
11.(3分) 若是关于x,y的二元一次方程,则的值为 .
12.(3分)如果实数满足方程组,那么 .
13.(3分)在方程中,如果用含有x的式子表示y,得 .
14.(3分)某商场出售甲、乙、丙三种型号的商品,若购买甲2件,乙3件,丙1件,共需130元;购买甲3件,乙5件,丙1件,共需205元.若购买甲,乙,丙各1件,则需 元.
15.(3分)我们知道,适合二元一次方程的一对未知数的值叫做这个二元一次方程的一个解.同样地,适合三元一次方程的一对未知数的值叫做这个三元一次方程的一个解.请写出方程的一个正整数解 .
16.(3分)一条船顺流航行,每小时行20km,逆流航行,每小时行16km,则船在静水的速度 km/h.
17.(3分)有甲、乙、丙三种商品,若购甲3件,乙2件,丙1件共需315元,购甲1件,乙2件,丙3件共需 285元,则购甲、乙、丙三种商品各一件共需 元.
18.(3分)村民小红家准备将一块良田分成A,B,C三个区域来种植三种畅销型农作物.爸爸计划好三个区域的占地面积后,小红主动承担起实地划分的任务.划分完毕后,爸爸发现粗心的小红将A区20%的面积划分给了B区,而原B区50%的面积错划分给了A区,C区面积未出错,造成现B区的面积占A,B两区面积和的比例达到了40%.为了协调三个区域的面积占比,爸爸只好将C区面积的40%分成两部分划分给现在的A区和B区.爸爸划分完后,A,B,C三个区域的面积比变为2:1:3,那么爸爸从C区划分给B区的面积与良田总面积的比为 .
三、解答题(共8题;共66分)
19.(8分)解方程组:
(1)(4分)
(2)(4分)
20.(6分)已知和 都是关于 x、y 的方程 y=kx+b 的解. 求 k、b 的值.
21.(6分)若方程是关于的二元一次方程,求的平方根.
22.(8分)小明给小红出了一道数学题:“如果我将二元一次方程组 第一个方程中y的系数遮住,第二个方程中x的系数遮住,并且告诉你 是这个方程组的解,你能求出我原来的方程组吗?”请你帮小红解答这个问题.
23.(8分)(我国古代算题)马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两,问马、牛各价几何
24.(8分)“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性,某粮食生产专业户去年计划生产小麦和玉米共18t,实际生产了20t,其中小麦超产12%,玉米超产10%,则该专业户去年实际生产小麦、玉米各多少吨?
25.(10分)2023年9月,第19届亚运会在杭州举行,本届亚运会吉祥物“宸宸”“琮琮”“莲莲”是一组承载深厚底蕴和充满时代活力的机器人.某纪念品店购进了一批亚运会吉祥物,其中“琮琮”“莲莲”共100个,花费4400元,这两种吉祥物的进价和售价如表:
吉祥物名称 琮琮 莲莲
进价(元/个) 40 50
售价(元/个) 60 65
(1)(5分)该纪念品店购进“琮琮”和“莲莲”各多少个?
(2)(5分)在(1)问的情况下,若把所购进的“琮琮”“莲莲”两种吉祥物全部销售完,利润率能否超过40%?请说明理由.
26.(12分)某景点的门票价格如表:
购票人数(人) 100以上
门票单价(元) 40 36 32
(1)(6分)某校七年级1、2两个班共有102人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付3868元,两个班各有多少名学生?如果两班联合起来作为一个团体购票能省多少钱?
(2)(6分)该校八、九年级自愿报名游览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人且不超过100人.若两个年级分别购票,总计支付门票费3600元;若合在一起作为一个团体购票,总计支付门票费3456元,问八年级、九年级各报名多少人?
答案解析部分
1.【答案】A
【知识点】二元一次方程组的解
【解析】【解答】解:根据题意,将代入原方程,得:,
解得:,
故答案为:A.
【分析】将代入原方程即可得一个关于的一元一次方程后解方程即可.
2.【答案】A
【知识点】二元一次方程组的解
【解析】【解答】解:由题意得:
把代入,得:,
∴得到;
∴被●和▲遮盖的两个数分别为5,1.
故选:A.
【分析】本题主要考查二元一次方程组解及其应用.先把代入,求得,再把和,代入,即可求得被●和▲遮盖的两个数,得到答案.
3.【答案】A
【知识点】列二元一次方程组
【解析】【解答】解:设竿长x尺,绳索长y尺,
由题意得,,
故选:A.
【分析】根据“绳索比竿长5尺”和“将绳索对折后再去量竿,就比竿短5尺”,分别列出方程式,即可求解.
4.【答案】C
【知识点】解二元一次方程组
【解析】【解答】解: 解得
故答案为:C.
【分析】直接将二元一次方程组的解求出来即可.
5.【答案】A
【知识点】加减消元法解二元一次方程组
【解析】【解答】解:若消去,
则得:;
若消去,
则得:;
故选:A.
【分析】本题考查加减消元法解方程组,加减消元法是指利用等式的性质,使方程组中两个方程中的某一个未知数前的系数的绝对值相等,然后把两个方程相加(或相减),以消去这个未知数,从而使方程只含有一个未知数,即可求解.
6.【答案】B
【知识点】三元一次方程组及其解法
【解析】【解答】解:,
得,x+y=z+6,
∵x+y=3,
∴z+6=3,
即z=-3.
故答案为:B.
【分析】用第二个方程减去第一个方程得到x+y=z+6,将x+y=3代入进行计算,即可得到答案.
7.【答案】A
【知识点】三元一次方程组及其解法
【解析】【解答】解:∵第一个方程只含有y,z,
∴对于方程组,
得到关于y,z的二元一次方程,联立第一个方程得到方程组,
∴最简单的做法是先消去x.
故答案为:A.
【分析】由题意可知第一个方程只含有y,z,利用第二、三个方程根据加减消元法消去x,即可得到关于y,z的二元一次方程,与第一个方程联立组成方程组即可得到答案.
8.【答案】C
【知识点】三元一次方程组及其解法
【解析】【解答】 解:由图可得,m=x+2x+y=3x+y,n=2x+y+3-2y=2x-y+3,
∴k=m+n
=(3x+y)+(2x-y+3)
=3x+y+2x-y+3
=5x+3,
∵k=8,
∴5x+3=8,
解得x=1.
故选:C.
【分析】 根据图形,可以用含x、y的式子表示出m、n;再用x、y的代数式表示出k,从而可以求得x的值.
9.【答案】A
【知识点】二元一次方程组的应用-古代数学问题
【解析】【解答】设木长尺,绳长尺,根据题意列方程组得
故答案为:A.
【分析】设木长尺,绳长尺,利用“一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺”列二元一次方程组即可.
10.【答案】C
【知识点】三元一次方程组的应用
【解析】【解答】解:设桌子的高度为hcm,第一个长方体的长为xcm,第二个长方体的宽为ycm,
由第一个图形可知桌子的高度为h-y+x=80,
由第二个图形可知桌子的高度为h-x+y=70,
两个方程相加得(h-y+x)+(h-x+y)=150,
解得h=75cm.
故答案为:C.
【分析】本题考查三元一次方程的解法.设桌子的高度为hcm,第一个长方体的长为xcm,第二个长方体的宽为ycm,根据量图形的高,可列出方程组h-y+x=80,h-x+y=70,两个方程相加可求出h的值,进而可求出答案.
11.【答案】2
【知识点】二元一次方程的概念
【解析】【解答】解:∵是关于x,y的二元一次方程,
∴a=1,b=1,
∴a+b=2,
故答案为:2
【分析】根据二元一次方程的定义结合题意即可得到a=1,b=1,进而相加即可求解。
12.【答案】8
【知识点】加减消元法解二元一次方程组
【解析】【解答】解:,
由①-②得;
故答案为:8.
【分析】利用整体求值法,①-②直接得到m-2n的值.
13.【答案】
【知识点】代入消元法解二元一次方程组
【解析】【解答】解:由方程,移项得,解得,
即用含有x的式子表示y,可得得,
故答案为:.
【分析】根据题意,移项得,结合多项式的运算性质,即可得到y关于x的表达式,得到答案.
14.【答案】55
【知识点】三元一次方程组解法及应用
【解析】【解答】解:设甲、乙、丙每件单价分别为x、y、z元,由题意可得:
,
②- ①得:
,
②-+①得:
,
④- ③×3得,
∴;
故填:55.
【分析】设甲、乙、丙每件单价分别为x、y、z元,建立方程组,整体求得的值.
15.【答案】或或
【知识点】三元一次方程组解法及应用
【解析】【解答】解:当时,成立;
当时,成立;
当时,成立;
故答案为:或或.
【分析】利用解三元一次方程的方法求解即可。
16.【答案】18
【知识点】二元一次方程组的实际应用-行程问题
【解析】【解答】解:设船在静水的速度为xkm/h,水流的速度为ykm/h,
因为 顺流航行,每小时行20km,逆流航行,每小时行16km,
可得方程组,解得: ,所以轮船在静水中的速度为18千米.
故答案为:18.
【分析】设船在静水的速度为xkm/h,水流的速度为ykm/h,根据题意,得出关于x,y的二元一次方程组,利用消元法求得不等式组的解,即可得到答案.
17.【答案】150
【知识点】三元一次方程组的应用
【解析】【解答】解:设一件甲商品x元,乙 y元,丙z元.
根据题意得
①+②得4x+4y+4z=600,
∴x+y+z=150,
故答案为:150.
【分析】设一件甲商品x元,乙 y元,丙z元,根据“购甲3件,乙2件,丙1件共需315元,购甲1件,乙2件,丙3件共需 285元”列出方程组,求出4x+4y+4z=600,再求出x+y+z=150即可.
18.【答案】
【知识点】三元一次方程组的应用
【解析】【解答】解:设爸爸计划A,B,C三个区域的面积分别为x,y,z.
则由小红将A区20%的面积划分给了B区,而原B区50%的面积错划分给了A区,造成现B区的面积占A、B两区面积和的比例达到了40%,
可列方程:y+20%x-50%y=40%(x+y),
解得y=2x,
则此时,A区:x-20%x+50%y=1.8x,
B区:y+20%x-50%y=1.2x,
C区:z,
由爸爸只好将C区面积的40%分成两部分划分给现在的A区和B区.爸爸划分完后,A,B,C三个区域的面积比变为2:1:3,
可列方程:1.8x+1.2x+40%z=z-40%z,
解得z=15x,
设将C区面积的40%分成两部分划分给现在的A区为m,则B区为6x-m.由三个区域的面积比变为2:1:3,可列方程:
1.8x+m=2[1.2x+(6x-m)],解得m=4.2x,
∴爸爸从C区划分给B区的面积为6x-m=1.8x,
则爸爸从C区划分给B区的面积与良田总面积的比为
故答案为:.
【分析】本题考查三元一次方程的解法.设爸爸计划A,B,C三个区域的面积分别为x,y,z.,根据
A、B两区面积和的比例达到了40%,可列方程:y+20%x-50%y=40%(x+y),进而可解得y=2x,此时可表示出A区:1.8x,B区:1.2x,C区:z,根据A,B,C三个区域的面积比变为2:1:3,可列方程:1.8x+1.2x+40%z=z-40%z,解得z=15x,设将C区面积的40%分成两部分划分给现在的A区为m,根据三个区域的面积比变为2:1:3,可列方程:1.8x+m=2[1.2x+(6x-m)],解得m=4.2x,据此可得从C区划分给B区的面积为6x-m=1.8x,进而可求出爸爸从C区划分给B区的面积与良田总面积的比.
19.【答案】(1)解:,
把①代入②得:,
解得:,
把代入①,得:,
所以原方程组的解为;
(2)解:,
由②得:③,
由③-①得:,
把代入①得:,
解得:,
所以原方程组的解为.
【知识点】代入消元法解二元一次方程组;加减消元法解二元一次方程组
【解析】【分析】(1)本题主要考查了解二元一次方程组,将代入,求得,再将其代入计算,求得x的值,即可得到答案;
(2)本题主要考查了解二元一次方程组,结合加减消元法求解,即可求解.
(1)解:,
把①代入②得:,
解得:,
把代入①,得:,
所以原方程组的解为;
(2)解:,
由②得:③,
由③-①得:,
把代入①得:,
解得:,
所以原方程组的解为.
20.【答案】解:∵和都是关于x、y的方程y=kx+b的解,
∴,解得.
【知识点】二元一次方程组的解
【解析】【分析】由题意把两组解代入方程y=kx+b可得关于k、b的二元一次方程组,解方程组即可求解.
21.【答案】解:由题意,得:,,
解得,.
所以.
故的平方根为.
【知识点】二元一次方程的概念
【解析】【分析】根据二元一次方程的定义:只含有2个未知数,未知数的项的次数是1的整式方程是二元一次方程,据此列出方程组,即可求出,,再代入计算后再根据平方根的定义求解即可.
22.【答案】解:设第①个方程y的系数为m,第②个方程x的系数为n,
∵ 是方程组的解,
∴ ,
解得 .
∴原来的方程组为
【知识点】二元一次方程组的解
【解析】【分析】将原方程组看做关于未知系数的方程组来解答即可.
23.【答案】解:设一匹马价x两,一头牛价y两,
由题意得:
解得:
答:一匹马价6两,一头牛价4两
【知识点】二元一次方程组的应用-古代数学问题
【解析】【分析】设一匹马价x两,一头牛价y两,根据题中的两个相等关系“四匹马+六头牛=48,三匹马+五头牛=38”可列关于x、y的方程组,解方程组即可求解.
24.【答案】解:设去年计划生产小麦t、玉米t,则去年小麦超产12%t,玉米超产10%t,根据题意,得解得
答:该专业户去年实际生产小麦10t、玉米8t。
【知识点】二元一次方程组的其他应用
【解析】【分析】设去年计划生产小麦t、玉米t,则去年小麦超产12%t,玉米超产10%t,根据去年计划生产小麦和玉米共18t ,列出方程x+y=18;再根据“实际生产了20t,其中小麦超产12%,玉米超产10%”列出方程12%x+10%y=20-18 ,组成方程组,再利用代入消元法解方程组,计算得到.
25.【答案】(1)解:设购进“琮琮”x个,购进“莲莲”y个,根据题意得:
,解得,,
答:该纪念品店购进“琮琮”60个,“莲莲”40个;
(2)解:能,理由如下:
,
∵,∴利润率能超过40%.
【知识点】二元一次方程组的实际应用-销售问题
【解析】【分析】(1)根据“ “琮琮”“莲莲”共100个,花费4400元”,可列出方程,解方程即可;
(2)根据(1)中结果,利用,求出利润率来,再和40%进行比较即可.
26.【答案】(1)解:设七年级1班人数为人,则2班人数为:人,由题意,得:,
解得:,
∴,
∴七年级1班人数为49人,则2班人数为53人;
联合购票,节省:(元)
答:七年级1班人数为49人,则2班人数为53人;联合购票,节省604元.
(2)解:设八年级报名人数为人,九年级报名人数为人,若,则:
,
解得:,不合题意,舍去;
∴,
∴,解得:,
答:八年级报名人数为人,九年级报名人数为人.
【知识点】一元一次方程的其他应用;二元一次方程组的实际应用-方案选择题问题
【解析】【分析】(1)设七年级1班人数为人,则2班人数为:人,根据门票单价结合一共支付的钱数即可列出方程,进而即可求解;
(2)设八年级报名人数为人,九年级报名人数为人,根据两种不同的购票方式即可列出二元一次方程组,进而解方程组即可。
(1)解:设七年级1班人数为人,则2班人数为:人,由题意,得:
,
解得:,
∴,
∴七年级1班人数为49人,则2班人数为53人;
联合购票,节省:(元)
答:七年级1班人数为49人,则2班人数为53人;联合购票,节省604元.
(2)设八年级报名人数为人,九年级报名人数为人,
若,则:,解得:,不合题意,舍去;
∴,
∴,解得:,
答:八年级报名人数为人,九年级报名人数为人.
华师大版七年级数学下册 第六章 一次方程组 单元测试题(2024)
一、选择题(共10题;共30分)
1.(3分)若是关于x和y的二元一次方程的解,则a的值是( )
A.3 B.4 C. D.
2.(3分)方程组的解为,则被●和▲遮盖的两个数分别为( )
A.5,1 B.1,3 C.2,3 D.2,4
3.(3分)我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )
A. B. C. D.
4.(3分)方程组 的解是 ( ).
A. B. C. D.
5.(3分)用加减消元法解方程组,下列做法正确的是( )
A. B. C. D.
6.(3分)已知 且 , 则 的值( )
A.为 9 B.为 -3 C.为 12 D.不确定
7.(3分)解三元一次方程组 , 时, 最简单的做法是( )
A.先消去 B.先消去 C.先消去 D.先消去常数
8.(3分)我们约定:上方相邻两数之和等于这两数下方箭头共同指向的数,如图1,有,在图2中,若的值为8,则的值为( )
A. B. C.1 D.任意实数
9.(3分)《孙子算经》中有一道题,原文是:今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?意思是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺.问木长多少尺?设木长尺,绳长尺,根据题意列方程组得( )
A. B. C. D.
10.(3分)如图,利用两块长方体木块测量一张桌子的高度.首先按图①的方式放置,再交换两木块的位置,按图②的方式放置,测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
二、填空题(共8题;共24分)
11.(3分) 若是关于x,y的二元一次方程,则的值为 .
12.(3分)如果实数满足方程组,那么 .
13.(3分)在方程中,如果用含有x的式子表示y,得 .
14.(3分)某商场出售甲、乙、丙三种型号的商品,若购买甲2件,乙3件,丙1件,共需130元;购买甲3件,乙5件,丙1件,共需205元.若购买甲,乙,丙各1件,则需 元.
15.(3分)我们知道,适合二元一次方程的一对未知数的值叫做这个二元一次方程的一个解.同样地,适合三元一次方程的一对未知数的值叫做这个三元一次方程的一个解.请写出方程的一个正整数解 .
16.(3分)一条船顺流航行,每小时行20km,逆流航行,每小时行16km,则船在静水的速度 km/h.
17.(3分)有甲、乙、丙三种商品,若购甲3件,乙2件,丙1件共需315元,购甲1件,乙2件,丙3件共需 285元,则购甲、乙、丙三种商品各一件共需 元.
18.(3分)村民小红家准备将一块良田分成A,B,C三个区域来种植三种畅销型农作物.爸爸计划好三个区域的占地面积后,小红主动承担起实地划分的任务.划分完毕后,爸爸发现粗心的小红将A区20%的面积划分给了B区,而原B区50%的面积错划分给了A区,C区面积未出错,造成现B区的面积占A,B两区面积和的比例达到了40%.为了协调三个区域的面积占比,爸爸只好将C区面积的40%分成两部分划分给现在的A区和B区.爸爸划分完后,A,B,C三个区域的面积比变为2:1:3,那么爸爸从C区划分给B区的面积与良田总面积的比为 .
三、解答题(共8题;共66分)
19.(8分)解方程组:
(1)(4分)
(2)(4分)
20.(6分)已知和 都是关于 x、y 的方程 y=kx+b 的解. 求 k、b 的值.
21.(6分)若方程是关于的二元一次方程,求的平方根.
22.(8分)小明给小红出了一道数学题:“如果我将二元一次方程组 第一个方程中y的系数遮住,第二个方程中x的系数遮住,并且告诉你 是这个方程组的解,你能求出我原来的方程组吗?”请你帮小红解答这个问题.
23.(8分)(我国古代算题)马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两,问马、牛各价几何
24.(8分)“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性,某粮食生产专业户去年计划生产小麦和玉米共18t,实际生产了20t,其中小麦超产12%,玉米超产10%,则该专业户去年实际生产小麦、玉米各多少吨?
25.(10分)2023年9月,第19届亚运会在杭州举行,本届亚运会吉祥物“宸宸”“琮琮”“莲莲”是一组承载深厚底蕴和充满时代活力的机器人.某纪念品店购进了一批亚运会吉祥物,其中“琮琮”“莲莲”共100个,花费4400元,这两种吉祥物的进价和售价如表:
吉祥物名称 琮琮 莲莲
进价(元/个) 40 50
售价(元/个) 60 65
(1)(5分)该纪念品店购进“琮琮”和“莲莲”各多少个?
(2)(5分)在(1)问的情况下,若把所购进的“琮琮”“莲莲”两种吉祥物全部销售完,利润率能否超过40%?请说明理由.
26.(12分)某景点的门票价格如表:
购票人数(人) 100以上
门票单价(元) 40 36 32
(1)(6分)某校七年级1、2两个班共有102人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付3868元,两个班各有多少名学生?如果两班联合起来作为一个团体购票能省多少钱?
(2)(6分)该校八、九年级自愿报名游览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人且不超过100人.若两个年级分别购票,总计支付门票费3600元;若合在一起作为一个团体购票,总计支付门票费3456元,问八年级、九年级各报名多少人?
答案解析部分
1.【答案】A
【知识点】二元一次方程组的解
【解析】【解答】解:根据题意,将代入原方程,得:,
解得:,
故答案为:A.
【分析】将代入原方程即可得一个关于的一元一次方程后解方程即可.
2.【答案】A
【知识点】二元一次方程组的解
【解析】【解答】解:由题意得:
把代入,得:,
∴得到;
∴被●和▲遮盖的两个数分别为5,1.
故选:A.
【分析】本题主要考查二元一次方程组解及其应用.先把代入,求得,再把和,代入,即可求得被●和▲遮盖的两个数,得到答案.
3.【答案】A
【知识点】列二元一次方程组
【解析】【解答】解:设竿长x尺,绳索长y尺,
由题意得,,
故选:A.
【分析】根据“绳索比竿长5尺”和“将绳索对折后再去量竿,就比竿短5尺”,分别列出方程式,即可求解.
4.【答案】C
【知识点】解二元一次方程组
【解析】【解答】解: 解得
故答案为:C.
【分析】直接将二元一次方程组的解求出来即可.
5.【答案】A
【知识点】加减消元法解二元一次方程组
【解析】【解答】解:若消去,
则得:;
若消去,
则得:;
故选:A.
【分析】本题考查加减消元法解方程组,加减消元法是指利用等式的性质,使方程组中两个方程中的某一个未知数前的系数的绝对值相等,然后把两个方程相加(或相减),以消去这个未知数,从而使方程只含有一个未知数,即可求解.
6.【答案】B
【知识点】三元一次方程组及其解法
【解析】【解答】解:,
得,x+y=z+6,
∵x+y=3,
∴z+6=3,
即z=-3.
故答案为:B.
【分析】用第二个方程减去第一个方程得到x+y=z+6,将x+y=3代入进行计算,即可得到答案.
7.【答案】A
【知识点】三元一次方程组及其解法
【解析】【解答】解:∵第一个方程只含有y,z,
∴对于方程组,
得到关于y,z的二元一次方程,联立第一个方程得到方程组,
∴最简单的做法是先消去x.
故答案为:A.
【分析】由题意可知第一个方程只含有y,z,利用第二、三个方程根据加减消元法消去x,即可得到关于y,z的二元一次方程,与第一个方程联立组成方程组即可得到答案.
8.【答案】C
【知识点】三元一次方程组及其解法
【解析】【解答】 解:由图可得,m=x+2x+y=3x+y,n=2x+y+3-2y=2x-y+3,
∴k=m+n
=(3x+y)+(2x-y+3)
=3x+y+2x-y+3
=5x+3,
∵k=8,
∴5x+3=8,
解得x=1.
故选:C.
【分析】 根据图形,可以用含x、y的式子表示出m、n;再用x、y的代数式表示出k,从而可以求得x的值.
9.【答案】A
【知识点】二元一次方程组的应用-古代数学问题
【解析】【解答】设木长尺,绳长尺,根据题意列方程组得
故答案为:A.
【分析】设木长尺,绳长尺,利用“一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺”列二元一次方程组即可.
10.【答案】C
【知识点】三元一次方程组的应用
【解析】【解答】解:设桌子的高度为hcm,第一个长方体的长为xcm,第二个长方体的宽为ycm,
由第一个图形可知桌子的高度为h-y+x=80,
由第二个图形可知桌子的高度为h-x+y=70,
两个方程相加得(h-y+x)+(h-x+y)=150,
解得h=75cm.
故答案为:C.
【分析】本题考查三元一次方程的解法.设桌子的高度为hcm,第一个长方体的长为xcm,第二个长方体的宽为ycm,根据量图形的高,可列出方程组h-y+x=80,h-x+y=70,两个方程相加可求出h的值,进而可求出答案.
11.【答案】2
【知识点】二元一次方程的概念
【解析】【解答】解:∵是关于x,y的二元一次方程,
∴a=1,b=1,
∴a+b=2,
故答案为:2
【分析】根据二元一次方程的定义结合题意即可得到a=1,b=1,进而相加即可求解。
12.【答案】8
【知识点】加减消元法解二元一次方程组
【解析】【解答】解:,
由①-②得;
故答案为:8.
【分析】利用整体求值法,①-②直接得到m-2n的值.
13.【答案】
【知识点】代入消元法解二元一次方程组
【解析】【解答】解:由方程,移项得,解得,
即用含有x的式子表示y,可得得,
故答案为:.
【分析】根据题意,移项得,结合多项式的运算性质,即可得到y关于x的表达式,得到答案.
14.【答案】55
【知识点】三元一次方程组解法及应用
【解析】【解答】解:设甲、乙、丙每件单价分别为x、y、z元,由题意可得:
,
②- ①得:
,
②-+①得:
,
④- ③×3得,
∴;
故填:55.
【分析】设甲、乙、丙每件单价分别为x、y、z元,建立方程组,整体求得的值.
15.【答案】或或
【知识点】三元一次方程组解法及应用
【解析】【解答】解:当时,成立;
当时,成立;
当时,成立;
故答案为:或或.
【分析】利用解三元一次方程的方法求解即可。
16.【答案】18
【知识点】二元一次方程组的实际应用-行程问题
【解析】【解答】解:设船在静水的速度为xkm/h,水流的速度为ykm/h,
因为 顺流航行,每小时行20km,逆流航行,每小时行16km,
可得方程组,解得: ,所以轮船在静水中的速度为18千米.
故答案为:18.
【分析】设船在静水的速度为xkm/h,水流的速度为ykm/h,根据题意,得出关于x,y的二元一次方程组,利用消元法求得不等式组的解,即可得到答案.
17.【答案】150
【知识点】三元一次方程组的应用
【解析】【解答】解:设一件甲商品x元,乙 y元,丙z元.
根据题意得
①+②得4x+4y+4z=600,
∴x+y+z=150,
故答案为:150.
【分析】设一件甲商品x元,乙 y元,丙z元,根据“购甲3件,乙2件,丙1件共需315元,购甲1件,乙2件,丙3件共需 285元”列出方程组,求出4x+4y+4z=600,再求出x+y+z=150即可.
18.【答案】
【知识点】三元一次方程组的应用
【解析】【解答】解:设爸爸计划A,B,C三个区域的面积分别为x,y,z.
则由小红将A区20%的面积划分给了B区,而原B区50%的面积错划分给了A区,造成现B区的面积占A、B两区面积和的比例达到了40%,
可列方程:y+20%x-50%y=40%(x+y),
解得y=2x,
则此时,A区:x-20%x+50%y=1.8x,
B区:y+20%x-50%y=1.2x,
C区:z,
由爸爸只好将C区面积的40%分成两部分划分给现在的A区和B区.爸爸划分完后,A,B,C三个区域的面积比变为2:1:3,
可列方程:1.8x+1.2x+40%z=z-40%z,
解得z=15x,
设将C区面积的40%分成两部分划分给现在的A区为m,则B区为6x-m.由三个区域的面积比变为2:1:3,可列方程:
1.8x+m=2[1.2x+(6x-m)],解得m=4.2x,
∴爸爸从C区划分给B区的面积为6x-m=1.8x,
则爸爸从C区划分给B区的面积与良田总面积的比为
故答案为:.
【分析】本题考查三元一次方程的解法.设爸爸计划A,B,C三个区域的面积分别为x,y,z.,根据
A、B两区面积和的比例达到了40%,可列方程:y+20%x-50%y=40%(x+y),进而可解得y=2x,此时可表示出A区:1.8x,B区:1.2x,C区:z,根据A,B,C三个区域的面积比变为2:1:3,可列方程:1.8x+1.2x+40%z=z-40%z,解得z=15x,设将C区面积的40%分成两部分划分给现在的A区为m,根据三个区域的面积比变为2:1:3,可列方程:1.8x+m=2[1.2x+(6x-m)],解得m=4.2x,据此可得从C区划分给B区的面积为6x-m=1.8x,进而可求出爸爸从C区划分给B区的面积与良田总面积的比.
19.【答案】(1)解:,
把①代入②得:,
解得:,
把代入①,得:,
所以原方程组的解为;
(2)解:,
由②得:③,
由③-①得:,
把代入①得:,
解得:,
所以原方程组的解为.
【知识点】代入消元法解二元一次方程组;加减消元法解二元一次方程组
【解析】【分析】(1)本题主要考查了解二元一次方程组,将代入,求得,再将其代入计算,求得x的值,即可得到答案;
(2)本题主要考查了解二元一次方程组,结合加减消元法求解,即可求解.
(1)解:,
把①代入②得:,
解得:,
把代入①,得:,
所以原方程组的解为;
(2)解:,
由②得:③,
由③-①得:,
把代入①得:,
解得:,
所以原方程组的解为.
20.【答案】解:∵和都是关于x、y的方程y=kx+b的解,
∴,解得.
【知识点】二元一次方程组的解
【解析】【分析】由题意把两组解代入方程y=kx+b可得关于k、b的二元一次方程组,解方程组即可求解.
21.【答案】解:由题意,得:,,
解得,.
所以.
故的平方根为.
【知识点】二元一次方程的概念
【解析】【分析】根据二元一次方程的定义:只含有2个未知数,未知数的项的次数是1的整式方程是二元一次方程,据此列出方程组,即可求出,,再代入计算后再根据平方根的定义求解即可.
22.【答案】解:设第①个方程y的系数为m,第②个方程x的系数为n,
∵ 是方程组的解,
∴ ,
解得 .
∴原来的方程组为
【知识点】二元一次方程组的解
【解析】【分析】将原方程组看做关于未知系数的方程组来解答即可.
23.【答案】解:设一匹马价x两,一头牛价y两,
由题意得:
解得:
答:一匹马价6两,一头牛价4两
【知识点】二元一次方程组的应用-古代数学问题
【解析】【分析】设一匹马价x两,一头牛价y两,根据题中的两个相等关系“四匹马+六头牛=48,三匹马+五头牛=38”可列关于x、y的方程组,解方程组即可求解.
24.【答案】解:设去年计划生产小麦t、玉米t,则去年小麦超产12%t,玉米超产10%t,根据题意,得解得
答:该专业户去年实际生产小麦10t、玉米8t。
【知识点】二元一次方程组的其他应用
【解析】【分析】设去年计划生产小麦t、玉米t,则去年小麦超产12%t,玉米超产10%t,根据去年计划生产小麦和玉米共18t ,列出方程x+y=18;再根据“实际生产了20t,其中小麦超产12%,玉米超产10%”列出方程12%x+10%y=20-18 ,组成方程组,再利用代入消元法解方程组,计算得到.
25.【答案】(1)解:设购进“琮琮”x个,购进“莲莲”y个,根据题意得:
,解得,,
答:该纪念品店购进“琮琮”60个,“莲莲”40个;
(2)解:能,理由如下:
,
∵,∴利润率能超过40%.
【知识点】二元一次方程组的实际应用-销售问题
【解析】【分析】(1)根据“ “琮琮”“莲莲”共100个,花费4400元”,可列出方程,解方程即可;
(2)根据(1)中结果,利用,求出利润率来,再和40%进行比较即可.
26.【答案】(1)解:设七年级1班人数为人,则2班人数为:人,由题意,得:,
解得:,
∴,
∴七年级1班人数为49人,则2班人数为53人;
联合购票,节省:(元)
答:七年级1班人数为49人,则2班人数为53人;联合购票,节省604元.
(2)解:设八年级报名人数为人,九年级报名人数为人,若,则:
,
解得:,不合题意,舍去;
∴,
∴,解得:,
答:八年级报名人数为人,九年级报名人数为人.
【知识点】一元一次方程的其他应用;二元一次方程组的实际应用-方案选择题问题
【解析】【分析】(1)设七年级1班人数为人,则2班人数为:人,根据门票单价结合一共支付的钱数即可列出方程,进而即可求解;
(2)设八年级报名人数为人,九年级报名人数为人,根据两种不同的购票方式即可列出二元一次方程组,进而解方程组即可。
(1)解:设七年级1班人数为人,则2班人数为:人,由题意,得:
,
解得:,
∴,
∴七年级1班人数为49人,则2班人数为53人;
联合购票,节省:(元)
答:七年级1班人数为49人,则2班人数为53人;联合购票,节省604元.
(2)设八年级报名人数为人,九年级报名人数为人,
若,则:,解得:,不合题意,舍去;
∴,
∴,解得:,
答:八年级报名人数为人,九年级报名人数为人.
