8.4机械能守恒定律课件高一下学期物理人教版(2019)必修第二册(共27张PPT)
文档属性
| 名称 | 8.4机械能守恒定律课件高一下学期物理人教版(2019)必修第二册(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 25.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-27 10:31:28 | ||
图片预览







文档简介
(共27张PPT)
第八章 机械能守恒定律
第4节 机械能守恒定律
1.知道机械能的概念。
2.理解机械能守恒定律的内容和守恒条件。
3.能用机械能守恒定律分析生活和生产中的有关问题。
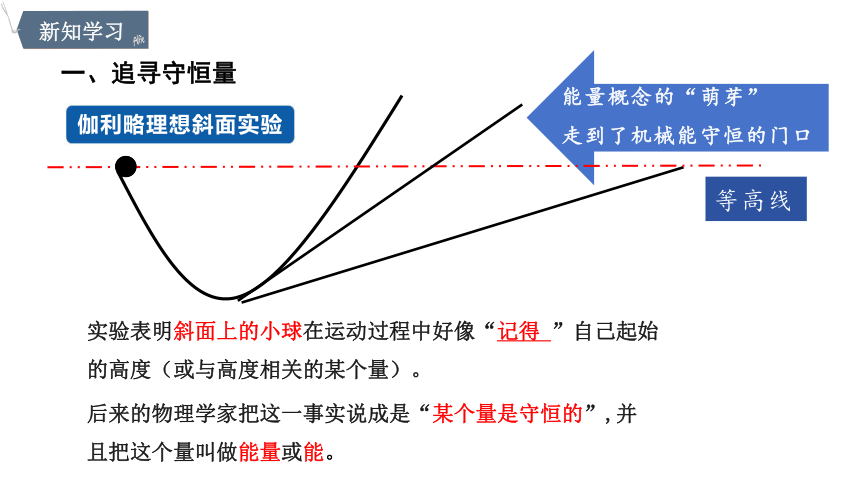
实验表明斜面上的小球在运动过程中好像“记得 ”自己起始的高度(或与高度相关的某个量)。
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
伽利略理想斜面实验
能量概念的“萌芽”
走到了机械能守恒的门口
等高线
一、追寻守恒量
A
B
h
h'
α
β
建模
一、追寻守恒量
【情境】两斜面光滑,小球在A斜面上高为h处静止滚下,在斜面B上速度为零时的高度为h' , h 和h' 的大小关系怎样?如果减小斜面B的倾角呢?
在A斜面上:
在B斜面上:
结果:
a=gsinα
x= v2/2a
h= x sinα=v2/2g
a'=-gsinβ
x' =(0-v2) /2a'
h'= x'sinβ = v2/2g
h'=h,
且与β角的
大小无关。
结论:后来物理学家把这一事实说成“某个量是守恒的”,并且把这个量叫做能量或能。
一、追寻守恒量
射箭运动
跳水运动
在以下体育比赛中,哪些能量之间发生了转化
撑杆跳运动
二、动能和势能的相互转化
A
C
B
问题1:小球的受力情况如何
问题2:由A到B过程中各个力做功情况如何?
问题3:由B到A过程中各个力做功情况如何?
问题4:这个实验说明了什么
1、动能与重力势能的相互转化
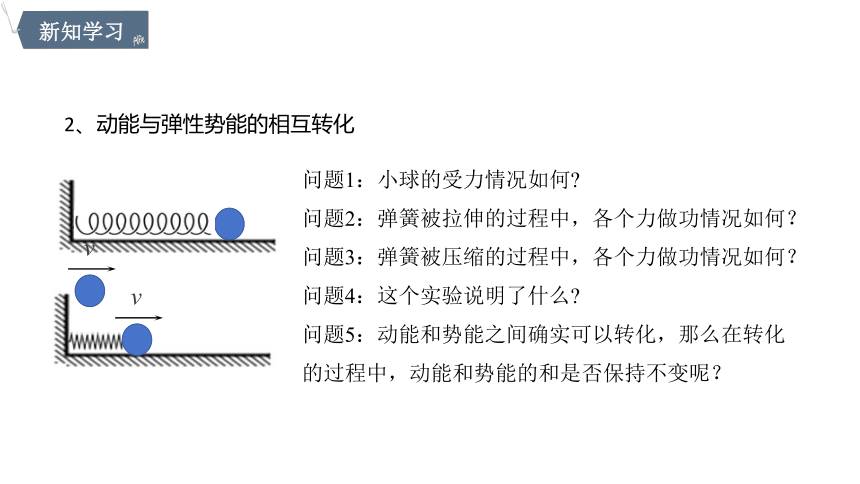
问题1:小球的受力情况如何
问题2:弹簧被拉伸的过程中,各个力做功情况如何?
问题3:弹簧被压缩的过程中,各个力做功情况如何?
问题4:这个实验说明了什么
问题5:动能和势能之间确实可以转化,那么在转化的过程中,动能和势能的和是否保持不变呢?
v
v
2、动能与弹性势能的相互转化
1.重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
机械能
2.
3 .机械能的性质:
⑴状态量
⑵相对性
⑶系统性
机械能的转化 通过重力或弹力做功实现的。
三、机械能
四、动能与势能相互转化
我们讨论物体沿光滑曲面滑下的情形。这种情形下,物体受到重力和曲面支持力的作用,因为支持力方向与运动方向垂直,支持力不做功,所以,只有重力做功。
情景1
四、动能与势能相互转化
1.举例推导
动能定理:
功能关系:
光滑曲面
联立变形:
【结论】只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
四、动能与势能相互转化
x
原长 2 1
光滑平面
2.举例推导
动能定理:
功能关系:
联立变形:
【结论】只有弹力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
情景2
一个小球在真空中做自由落体运动,另一个同样的小球在黏性较大的液体中由静止开始下落。它们都由高度为 h1 的地方下落到高度为 h2 的地方。
在这两种情况下,重力做的功相等吗?重力势能的变化相等吗?动能的变化相等吗?重力势能各转化成什么形式的能?
情景3
3.总结归纳
动能定理:
功能关系:
W非=0
五、机械能守恒定律
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变。
3.表达式:
4.机械能守恒的条件:只有重力或弹力做功
1.内容:
E2=E1
EP2+EK2=EP1+EK1
2.研究对象: 系统
机械能守恒判断
1.抛体模型(不计一切摩擦)
竖直上抛
竖直下抛
斜上抛
平抛
斜下抛
(1)小球抛出后机械能是否守恒?
守恒
机械能守恒判断
2.含弹簧模型(弹簧质量不计)
释放小球后,小球与弹簧组成的系统机械能守恒吗?
守恒
机械能守恒判断
3.板块模型
(1)若A固定在水平面上,且不计一切摩擦。B机械能守恒吗?
(2)若A未固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
B机械能守恒吗?
守恒
守恒
不守恒
机械能守恒判断
4.绳杆模型(轻绳、轻杆)
(1)若斜面体固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
(1)球A、球B组成的系统机械能守恒吗?
(2)球A机械能守恒吗?若不守恒机械能怎么变?
守恒
守恒
不守恒,机械能变小
机械能守恒定律的应用
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件:
方法1 研究对象在运动过程中是否只有重力或弹力做功
方法2研究对象在运动过 程中是否只有动能、势能的转化
3.应用机械能守恒定律解决问题
EP2+EK2=EP1+EK1
1、在下列的物理过程中,机械能守恒的有( )
A.一小球在粘滞性较大的液体中匀速下落
B.用细线拴着一个小球竖直平面内做圆周运动
C.物体在光滑斜面上自由下滑
D.拉着一个物体沿着光滑斜面匀速上升
BC
2.如图所示,桌面离地高为h,质量为m的小球从离桌面高H处自由下落,不计空气阻力,假设桌面为零势能的参考平面,则小球落地前瞬间的机械能为 ( )
A.mgh B.mgH
C.mg(h+H) D. mg(H-h)
B
3.一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦、空气阻力均不计,重力加速度为g)。
研究对象:A、B组成的系统
A上升、B下落到刚要落地的过程中,A与B的速率时刻相等
在B下落A上升的过程中, A、B组成的系统机械能守恒
以地面为零势能参考面
E1=mBgh
系统的初状态的机械能
末状态的机械能
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件
3.应用机械能守恒定律解决问题
3.一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
解:对A、B组成的系统,A上升、B下落到刚要落地的过程
系统机械能守恒,以地面为零势能参考面
由E2=E1可知
所以:v= = =2 m/s
方法1 由E2=E1解决问题
3.一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
方法1 由E2=E1解决问题
方法2 由ΔEk=-ΔEp解决问题
方法3 由ΔEA=-ΔEB解决问题
概 念:
表达式:E=Ek+Ep
机械能是标量,具有相对性
定律内容
表达式
条件:只有重力或弹簧弹力做功。
机械能是动能、重力势能、弹性势能的统称
机械能守恒定律
机械能
E1=E2
Ep2+Ek2=Ep1+Ek1
=
第八章 机械能守恒定律
第4节 机械能守恒定律
1.知道机械能的概念。
2.理解机械能守恒定律的内容和守恒条件。
3.能用机械能守恒定律分析生活和生产中的有关问题。
实验表明斜面上的小球在运动过程中好像“记得 ”自己起始的高度(或与高度相关的某个量)。
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
伽利略理想斜面实验
能量概念的“萌芽”
走到了机械能守恒的门口
等高线
一、追寻守恒量
A
B
h
h'
α
β
建模
一、追寻守恒量
【情境】两斜面光滑,小球在A斜面上高为h处静止滚下,在斜面B上速度为零时的高度为h' , h 和h' 的大小关系怎样?如果减小斜面B的倾角呢?
在A斜面上:
在B斜面上:
结果:
a=gsinα
x= v2/2a
h= x sinα=v2/2g
a'=-gsinβ
x' =(0-v2) /2a'
h'= x'sinβ = v2/2g
h'=h,
且与β角的
大小无关。
结论:后来物理学家把这一事实说成“某个量是守恒的”,并且把这个量叫做能量或能。
一、追寻守恒量
射箭运动
跳水运动
在以下体育比赛中,哪些能量之间发生了转化
撑杆跳运动
二、动能和势能的相互转化
A
C
B
问题1:小球的受力情况如何
问题2:由A到B过程中各个力做功情况如何?
问题3:由B到A过程中各个力做功情况如何?
问题4:这个实验说明了什么
1、动能与重力势能的相互转化
问题1:小球的受力情况如何
问题2:弹簧被拉伸的过程中,各个力做功情况如何?
问题3:弹簧被压缩的过程中,各个力做功情况如何?
问题4:这个实验说明了什么
问题5:动能和势能之间确实可以转化,那么在转化的过程中,动能和势能的和是否保持不变呢?
v
v
2、动能与弹性势能的相互转化
1.重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
机械能
2.
3 .机械能的性质:
⑴状态量
⑵相对性
⑶系统性
机械能的转化 通过重力或弹力做功实现的。
三、机械能
四、动能与势能相互转化
我们讨论物体沿光滑曲面滑下的情形。这种情形下,物体受到重力和曲面支持力的作用,因为支持力方向与运动方向垂直,支持力不做功,所以,只有重力做功。
情景1
四、动能与势能相互转化
1.举例推导
动能定理:
功能关系:
光滑曲面
联立变形:
【结论】只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
四、动能与势能相互转化
x
原长 2 1
光滑平面
2.举例推导
动能定理:
功能关系:
联立变形:
【结论】只有弹力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
情景2
一个小球在真空中做自由落体运动,另一个同样的小球在黏性较大的液体中由静止开始下落。它们都由高度为 h1 的地方下落到高度为 h2 的地方。
在这两种情况下,重力做的功相等吗?重力势能的变化相等吗?动能的变化相等吗?重力势能各转化成什么形式的能?
情景3
3.总结归纳
动能定理:
功能关系:
W非=0
五、机械能守恒定律
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变。
3.表达式:
4.机械能守恒的条件:只有重力或弹力做功
1.内容:
E2=E1
EP2+EK2=EP1+EK1
2.研究对象: 系统
机械能守恒判断
1.抛体模型(不计一切摩擦)
竖直上抛
竖直下抛
斜上抛
平抛
斜下抛
(1)小球抛出后机械能是否守恒?
守恒
机械能守恒判断
2.含弹簧模型(弹簧质量不计)
释放小球后,小球与弹簧组成的系统机械能守恒吗?
守恒
机械能守恒判断
3.板块模型
(1)若A固定在水平面上,且不计一切摩擦。B机械能守恒吗?
(2)若A未固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
B机械能守恒吗?
守恒
守恒
不守恒
机械能守恒判断
4.绳杆模型(轻绳、轻杆)
(1)若斜面体固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
(1)球A、球B组成的系统机械能守恒吗?
(2)球A机械能守恒吗?若不守恒机械能怎么变?
守恒
守恒
不守恒,机械能变小
机械能守恒定律的应用
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件:
方法1 研究对象在运动过程中是否只有重力或弹力做功
方法2研究对象在运动过 程中是否只有动能、势能的转化
3.应用机械能守恒定律解决问题
EP2+EK2=EP1+EK1
1、在下列的物理过程中,机械能守恒的有( )
A.一小球在粘滞性较大的液体中匀速下落
B.用细线拴着一个小球竖直平面内做圆周运动
C.物体在光滑斜面上自由下滑
D.拉着一个物体沿着光滑斜面匀速上升
BC
2.如图所示,桌面离地高为h,质量为m的小球从离桌面高H处自由下落,不计空气阻力,假设桌面为零势能的参考平面,则小球落地前瞬间的机械能为 ( )
A.mgh B.mgH
C.mg(h+H) D. mg(H-h)
B
3.一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦、空气阻力均不计,重力加速度为g)。
研究对象:A、B组成的系统
A上升、B下落到刚要落地的过程中,A与B的速率时刻相等
在B下落A上升的过程中, A、B组成的系统机械能守恒
以地面为零势能参考面
E1=mBgh
系统的初状态的机械能
末状态的机械能
1.确定研究对象(物体系统)和要研究的过程
2.判断是否符合机械能守恒的条件
3.应用机械能守恒定律解决问题
3.一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
解:对A、B组成的系统,A上升、B下落到刚要落地的过程
系统机械能守恒,以地面为零势能参考面
由E2=E1可知
所以:v= = =2 m/s
方法1 由E2=E1解决问题
3.一条轻绳跨过定滑轮,绳的两端各系一个小球A和B,B球的质量是A球的质量的3倍。用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h,A球静止于地面,如图所示。现释放B球,当B球刚落地时,求A球的速度大小(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
方法1 由E2=E1解决问题
方法2 由ΔEk=-ΔEp解决问题
方法3 由ΔEA=-ΔEB解决问题
概 念:
表达式:E=Ek+Ep
机械能是标量,具有相对性
定律内容
表达式
条件:只有重力或弹簧弹力做功。
机械能是动能、重力势能、弹性势能的统称
机械能守恒定律
机械能
E1=E2
Ep2+Ek2=Ep1+Ek1
=
