【备课无忧】人教版四下-1.3 含括号的四则混合运算(教学课件)
文档属性
| 名称 | 【备课无忧】人教版四下-1.3 含括号的四则混合运算(教学课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 10:35:49 | ||
图片预览






文档简介
(共24张PPT)
人教版数学四年级下册
第
一
单
元
3.含括号的四则混合运算
想一想,你学过哪些运算?
+
-
×
÷
一级运算
二级运算
加、减、乘、除四种运算统称四则运算。
说说下面各题的运算顺序,并计算出来。
(1)7×2+30
(2)175-25×4
(3)40÷4+6
(4)48-18÷2
=14+30
=44
=175-100
=75
=10+6
=16
=48-9
=39
两级运算,先算乘除,后算加减。
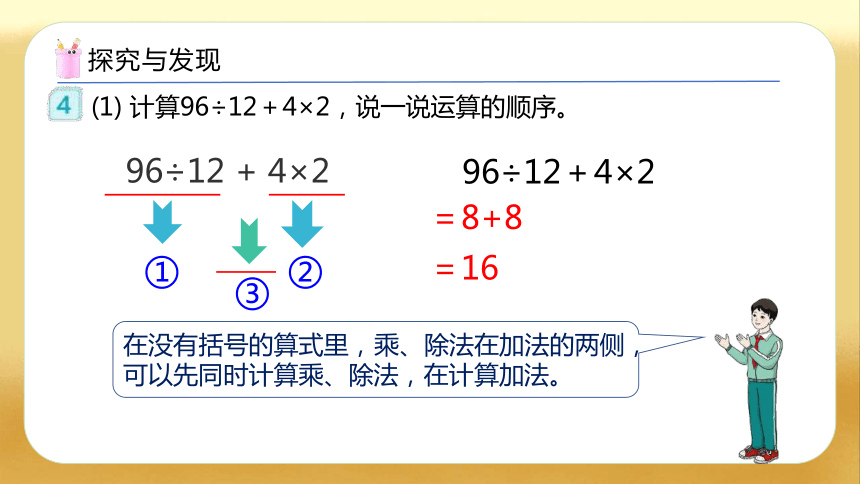
(1) 计算96÷12+4×2,说一说运算的顺序。
96÷12 + 4×2
①
②
③
=8+8
=16
96÷12+4×2
在没有括号的算式里,乘、除法在加法的两侧,可以先同时计算乘、除法,在计算加法。
(2)在算式96÷12+4×2中加个小括号,变成 96÷(12+4)×2,运算顺序变了吗?
96÷(12+4)×2
①
②
③
=96÷16×2
=6×2
96÷(12+4)×2
=12
96÷[(12+4)×2]
①
②
③
“[ ]”叫做中括号。它的作用与小括号一样,也是改变混合运算的运算顺序,当一个算式用了小括号后,还需要改变运算顺序,就要使用中括号。
(3)在96÷(12+4)×2的基础上加上中括号“[ ]”,变成另一个算式96÷[(12+4)×2],运算顺序变了吗?
96÷[(12+4)×2]
=96÷[16×2]
=96÷32
=3
先算小括号里的
最后算括号外的
再算中括号里的
一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的。
(3)在96÷(12+4)×2的基础上加上中括号“[ ]”,变成另一个算式96÷[(12+4)×2],运算顺序变了吗?
小括号“( )”是公元17世纪由荷兰人吉拉特首先使用的。
中括号“[ ]”是公元17世纪英国数学家瓦力士最先使用的。
在以后的学习中,还会用到大括号“{ }”,又称为花括号。大括号是法国教数学家韦达在1593年首先使用的。
◎
◎
你知道吗?
归纳总结:
(1)有括号的算式,要先算括号里面的。
(2)一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的。
【教材第9页“做一做”】
1.先说一说运算顺序再计算。
360÷(70-4×16)
360÷(70-4×16)
①
③
②
=360÷(70-64)
=360÷6
=60
168÷[(28+44)÷9]
168÷[(28+44)÷9]
①
③
②
=168-[72÷9]
=168-8
=160
【教材P11 练习三 第2题】
2.按照顺序计算,并填写下面的 ,然后列出综合算式。
128
147
25
320
+
÷
×
438
73
920
34
+
÷
×
算式:
算式:
275
11
3520
6
926
31484
320×[(128+147)÷25]=3520
(920+438÷73)×34=31484
3.填一填。
(1)计算(230+48)÷(200-61)时,应先算( )法和( )法,最后算( )法。
(2)计算888÷[200-(40+50)]时,应先算( )法,再算( )法,最后算( )法。
加
减
除
加
减
除
4.根据运算顺序,在题目中添上小括号或中括号。
16 × 600 – 200 ÷ 50 先除再减最后乘
16 × 600 – 200 ÷ 50 先减再乘最后除
16 × 600 – 200 ÷ 50 先减再除最后乘
[ ]
( )
( )
[ ]
( )
5.一辆汽车8小时行驶640千米,一架飞机2小时飞行1600千米,飞机的速度是汽车速度的几倍?
方法1: 640÷8=80(千米)
1600÷2=800(千米)
800÷80=10
方法2:(1600÷2)÷(640÷8)
= 800÷80
= 10
答:飞机速度是汽车的10倍。
点击输入标题
点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。
点击此处输入标题
今天我学会了……
课堂总结
没有括号,先算乘、除,再算加、减。
在一个算式里,既有小括号又有中括号,要先算小括号里面的,再算中括号里面的。
学习态度
学习自信
学习合作
素养评价
1.完成《分层作业》中对应练习。
2.预习下一节内容。
课后作业
课程结束
人教版数学四年级下册
第
一
单
元
3.含括号的四则混合运算
想一想,你学过哪些运算?
+
-
×
÷
一级运算
二级运算
加、减、乘、除四种运算统称四则运算。
说说下面各题的运算顺序,并计算出来。
(1)7×2+30
(2)175-25×4
(3)40÷4+6
(4)48-18÷2
=14+30
=44
=175-100
=75
=10+6
=16
=48-9
=39
两级运算,先算乘除,后算加减。
(1) 计算96÷12+4×2,说一说运算的顺序。
96÷12 + 4×2
①
②
③
=8+8
=16
96÷12+4×2
在没有括号的算式里,乘、除法在加法的两侧,可以先同时计算乘、除法,在计算加法。
(2)在算式96÷12+4×2中加个小括号,变成 96÷(12+4)×2,运算顺序变了吗?
96÷(12+4)×2
①
②
③
=96÷16×2
=6×2
96÷(12+4)×2
=12
96÷[(12+4)×2]
①
②
③
“[ ]”叫做中括号。它的作用与小括号一样,也是改变混合运算的运算顺序,当一个算式用了小括号后,还需要改变运算顺序,就要使用中括号。
(3)在96÷(12+4)×2的基础上加上中括号“[ ]”,变成另一个算式96÷[(12+4)×2],运算顺序变了吗?
96÷[(12+4)×2]
=96÷[16×2]
=96÷32
=3
先算小括号里的
最后算括号外的
再算中括号里的
一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的。
(3)在96÷(12+4)×2的基础上加上中括号“[ ]”,变成另一个算式96÷[(12+4)×2],运算顺序变了吗?
小括号“( )”是公元17世纪由荷兰人吉拉特首先使用的。
中括号“[ ]”是公元17世纪英国数学家瓦力士最先使用的。
在以后的学习中,还会用到大括号“{ }”,又称为花括号。大括号是法国教数学家韦达在1593年首先使用的。
◎
◎
你知道吗?
归纳总结:
(1)有括号的算式,要先算括号里面的。
(2)一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的。
【教材第9页“做一做”】
1.先说一说运算顺序再计算。
360÷(70-4×16)
360÷(70-4×16)
①
③
②
=360÷(70-64)
=360÷6
=60
168÷[(28+44)÷9]
168÷[(28+44)÷9]
①
③
②
=168-[72÷9]
=168-8
=160
【教材P11 练习三 第2题】
2.按照顺序计算,并填写下面的 ,然后列出综合算式。
128
147
25
320
+
÷
×
438
73
920
34
+
÷
×
算式:
算式:
275
11
3520
6
926
31484
320×[(128+147)÷25]=3520
(920+438÷73)×34=31484
3.填一填。
(1)计算(230+48)÷(200-61)时,应先算( )法和( )法,最后算( )法。
(2)计算888÷[200-(40+50)]时,应先算( )法,再算( )法,最后算( )法。
加
减
除
加
减
除
4.根据运算顺序,在题目中添上小括号或中括号。
16 × 600 – 200 ÷ 50 先除再减最后乘
16 × 600 – 200 ÷ 50 先减再乘最后除
16 × 600 – 200 ÷ 50 先减再除最后乘
[ ]
( )
( )
[ ]
( )
5.一辆汽车8小时行驶640千米,一架飞机2小时飞行1600千米,飞机的速度是汽车速度的几倍?
方法1: 640÷8=80(千米)
1600÷2=800(千米)
800÷80=10
方法2:(1600÷2)÷(640÷8)
= 800÷80
= 10
答:飞机速度是汽车的10倍。
点击输入标题
点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。点此输入内容或者复制您的内容在这里,在此框中选择粘贴,并选择只保留文字。
点击此处输入标题
今天我学会了……
课堂总结
没有括号,先算乘、除,再算加、减。
在一个算式里,既有小括号又有中括号,要先算小括号里面的,再算中括号里面的。
学习态度
学习自信
学习合作
素养评价
1.完成《分层作业》中对应练习。
2.预习下一节内容。
课后作业
课程结束
