【备课无忧】人教版四下-9.1 数学广角-鸡兔同笼(教学设计含反思)
文档属性
| 名称 | 【备课无忧】人教版四下-9.1 数学广角-鸡兔同笼(教学设计含反思) |
|
|
| 格式 | docx | ||
| 文件大小 | 16.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 00:00:00 | ||
图片预览


文档简介
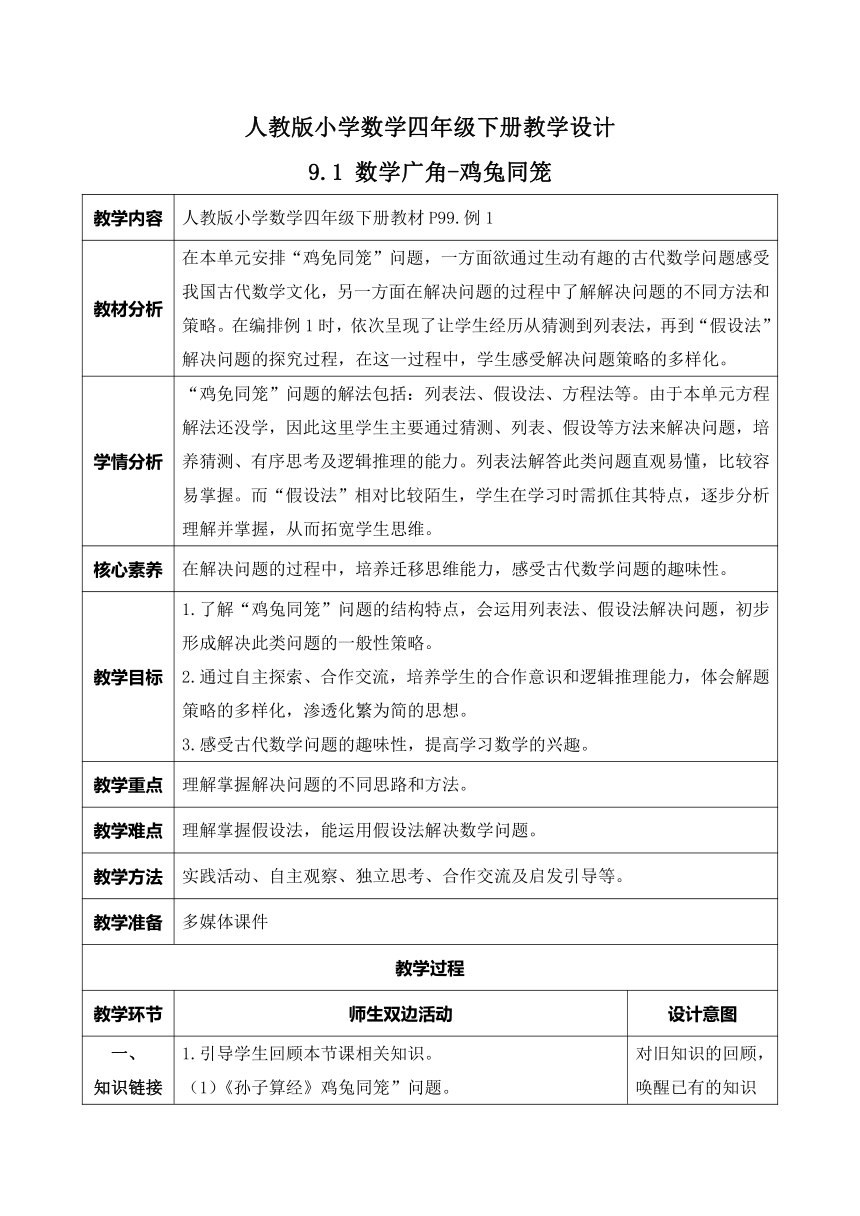
人教版小学数学四年级下册教学设计
9.1 数学广角-鸡兔同笼
教学内容 人教版小学数学四年级下册教材P99.例1
教材分析 在本单元安排“鸡免同笼”问题,一方面欲通过生动有趣的古代数学问题感受我国古代数学文化,另一方面在解决问题的过程中了解解决问题的不同方法和策略。在编排例1时,依次呈现了让学生经历从猜测到列表法,再到“假设法”解决问题的探究过程,在这一过程中,学生感受解决问题策略的多样化。
学情分析 “鸡免同笼”问题的解法包括:列表法、假设法、方程法等。由于本单元方程解法还没学,因此这里学生主要通过猜测、列表、假设等方法来解决问题,培养猜测、有序思考及逻辑推理的能力。列表法解答此类问题直观易懂,比较容易掌握。而“假设法”相对比较陌生,学生在学习时需抓住其特点,逐步分析理解并掌握,从而拓宽学生思维。
核心素养 在解决问题的过程中,培养迁移思维能力,感受古代数学问题的趣味性。
教学目标 1.了解“鸡兔同笼”问题的结构特点,会运用列表法、假设法解决问题,初步形成解决此类问题的一般性策略。 2.通过自主探索、合作交流,培养学生的合作意识和逻辑推理能力,体会解题策略的多样化,渗透化繁为简的思想。 3.感受古代数学问题的趣味性,提高学习数学的兴趣。
教学重点 理解掌握解决问题的不同思路和方法。
教学难点 理解掌握假设法,能运用假设法解决数学问题。
教学方法 实践活动、自主观察、独立思考、合作交流及启发引导等。
教学准备 多媒体课件
教学过程
教学环节 师生双边活动 设计意图
一、 知识链接 1.引导学生回顾本节课相关知识。 (1)《孙子算经》鸡兔同笼”问题。 (2)想一想:请你猜一猜,大概有多少只鸡,多少只兔? 2.小结,引出课题。 对旧知识的回顾,唤醒已有的知识经验,做好前测,为探究新知做好准备。
二、 探究新知 教学例1. 1.课件教材情境图。 请大家仔细看一看,题目中有那些数学信息? 生:鸡和兔共有8个头,26条腿。还有1只鸡有2条腿,1只兔有4条腿。 (一)列表法 师:要想知道鸡和兔各有多少只,这个问题您想怎么解决? 学生尝试猜测。 填写表格。 仔细观察表格你发现了什么规律?小组交流讨论。 (二)假设法。 师:老师有一个非常有趣的解法,您想不想知道? 生:想。 师:鸡和兔一共多少只?共有多少条腿? 生:一共有8只,26条腿。 师:如果所有的兔子都站了起来会是什么情况?我们再数一数一共会有多少条腿? 生:16条 师:这16条腿再和实际的26条比一比的话少了多少条? 生:10条。 师:为什么会少这10条腿?是谁的? 生:兔子的。 师:10只脚是多少只兔子的腿? 生:5只。 师:您怎么算的? 生:10÷2. 师:刚才的过程您能用算式表示出来吗?(学生列式) 师:刚才让所有的兔子都站起来也就相当于把所有的只数都看成了什么?如果把所有的只数都看成兔呢?会是什么情况啊? 师:大家能不能用算式表示出这个过程呢?(学生思考并列式) 师:为了解决问题我们可以把鸡看成兔,也可以把兔看成鸡,这种方法可以叫作假设法。 师:我们今天用列表法和假设法解决了鸡兔同笼问题,列表法当数据较大时,过程就很麻烦。假设法具有一般性,不管是数据较大时或数据较小时都可用到这个方法。那现在我们用学到的方法来解决一下《孙子算经》中的原题。 让学生以填表的方式初步体验鸡兔同笼情况下随着鸡或兔只数的调整,脚的总数量的变化规律,为下面的学习做好铺垫。 放手让学生合作探究,学生从尝试到讨论、汇报,结合课件的直观演示,学生个人或集体的智慧在这里可以得到充分的展现。
三、 课堂演练 基础演练: 1.完成教材第101页“练习二十四”第2题。 2.完成教材第101页“练习二十四”第4题。 3.完成教材第106页“练习二十四”第1题。 拓展延伸: 分层次的巩固练习有助于对学生知识掌握和能力发展进行评价。
四、 总结评价 1.这节课你学会了什么,怎么学会的? 引导学生总结梳理所学知识,养成良好的数学学习习惯。
板书设计 数学广角-鸡兔同笼 (一) 列表法 (二) 假设法
课后作业 1.从课本习题中选取; 2.完成练习册本课时的习题。
课后反思 由于学生原有认知背景的不同,他们对解答本课时的题目存在较大的差异,所以,在同样的列表中,学生的认知水平也有一定的层次,但大部分同学都能从列表法中找到答案。在教学的过程中,我并没有提出统一的要求,允许不同的学生采用不同的解题方法。在交流时,有些学生用假设方法,还有的用方程法,无论什么样的方法我都给以肯定,但在总结时则引导学生选择最优的方法去解决问题,这样做的目的是,不同的学生在同一节课中就会都有不同程度地提高。
9.1 数学广角-鸡兔同笼
教学内容 人教版小学数学四年级下册教材P99.例1
教材分析 在本单元安排“鸡免同笼”问题,一方面欲通过生动有趣的古代数学问题感受我国古代数学文化,另一方面在解决问题的过程中了解解决问题的不同方法和策略。在编排例1时,依次呈现了让学生经历从猜测到列表法,再到“假设法”解决问题的探究过程,在这一过程中,学生感受解决问题策略的多样化。
学情分析 “鸡免同笼”问题的解法包括:列表法、假设法、方程法等。由于本单元方程解法还没学,因此这里学生主要通过猜测、列表、假设等方法来解决问题,培养猜测、有序思考及逻辑推理的能力。列表法解答此类问题直观易懂,比较容易掌握。而“假设法”相对比较陌生,学生在学习时需抓住其特点,逐步分析理解并掌握,从而拓宽学生思维。
核心素养 在解决问题的过程中,培养迁移思维能力,感受古代数学问题的趣味性。
教学目标 1.了解“鸡兔同笼”问题的结构特点,会运用列表法、假设法解决问题,初步形成解决此类问题的一般性策略。 2.通过自主探索、合作交流,培养学生的合作意识和逻辑推理能力,体会解题策略的多样化,渗透化繁为简的思想。 3.感受古代数学问题的趣味性,提高学习数学的兴趣。
教学重点 理解掌握解决问题的不同思路和方法。
教学难点 理解掌握假设法,能运用假设法解决数学问题。
教学方法 实践活动、自主观察、独立思考、合作交流及启发引导等。
教学准备 多媒体课件
教学过程
教学环节 师生双边活动 设计意图
一、 知识链接 1.引导学生回顾本节课相关知识。 (1)《孙子算经》鸡兔同笼”问题。 (2)想一想:请你猜一猜,大概有多少只鸡,多少只兔? 2.小结,引出课题。 对旧知识的回顾,唤醒已有的知识经验,做好前测,为探究新知做好准备。
二、 探究新知 教学例1. 1.课件教材情境图。 请大家仔细看一看,题目中有那些数学信息? 生:鸡和兔共有8个头,26条腿。还有1只鸡有2条腿,1只兔有4条腿。 (一)列表法 师:要想知道鸡和兔各有多少只,这个问题您想怎么解决? 学生尝试猜测。 填写表格。 仔细观察表格你发现了什么规律?小组交流讨论。 (二)假设法。 师:老师有一个非常有趣的解法,您想不想知道? 生:想。 师:鸡和兔一共多少只?共有多少条腿? 生:一共有8只,26条腿。 师:如果所有的兔子都站了起来会是什么情况?我们再数一数一共会有多少条腿? 生:16条 师:这16条腿再和实际的26条比一比的话少了多少条? 生:10条。 师:为什么会少这10条腿?是谁的? 生:兔子的。 师:10只脚是多少只兔子的腿? 生:5只。 师:您怎么算的? 生:10÷2. 师:刚才的过程您能用算式表示出来吗?(学生列式) 师:刚才让所有的兔子都站起来也就相当于把所有的只数都看成了什么?如果把所有的只数都看成兔呢?会是什么情况啊? 师:大家能不能用算式表示出这个过程呢?(学生思考并列式) 师:为了解决问题我们可以把鸡看成兔,也可以把兔看成鸡,这种方法可以叫作假设法。 师:我们今天用列表法和假设法解决了鸡兔同笼问题,列表法当数据较大时,过程就很麻烦。假设法具有一般性,不管是数据较大时或数据较小时都可用到这个方法。那现在我们用学到的方法来解决一下《孙子算经》中的原题。 让学生以填表的方式初步体验鸡兔同笼情况下随着鸡或兔只数的调整,脚的总数量的变化规律,为下面的学习做好铺垫。 放手让学生合作探究,学生从尝试到讨论、汇报,结合课件的直观演示,学生个人或集体的智慧在这里可以得到充分的展现。
三、 课堂演练 基础演练: 1.完成教材第101页“练习二十四”第2题。 2.完成教材第101页“练习二十四”第4题。 3.完成教材第106页“练习二十四”第1题。 拓展延伸: 分层次的巩固练习有助于对学生知识掌握和能力发展进行评价。
四、 总结评价 1.这节课你学会了什么,怎么学会的? 引导学生总结梳理所学知识,养成良好的数学学习习惯。
板书设计 数学广角-鸡兔同笼 (一) 列表法 (二) 假设法
课后作业 1.从课本习题中选取; 2.完成练习册本课时的习题。
课后反思 由于学生原有认知背景的不同,他们对解答本课时的题目存在较大的差异,所以,在同样的列表中,学生的认知水平也有一定的层次,但大部分同学都能从列表法中找到答案。在教学的过程中,我并没有提出统一的要求,允许不同的学生采用不同的解题方法。在交流时,有些学生用假设方法,还有的用方程法,无论什么样的方法我都给以肯定,但在总结时则引导学生选择最优的方法去解决问题,这样做的目的是,不同的学生在同一节课中就会都有不同程度地提高。
