第五单元 整理与复习 单元测试卷 浙教版六年级数学下册(含答案)
文档属性
| 名称 | 第五单元 整理与复习 单元测试卷 浙教版六年级数学下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 180.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 00:00:00 | ||
图片预览




文档简介
第五单元 整理与复习 单元测试卷
一、单选题
1.下面的比中能与3:8组成比例的是( )。
A.3.5:6 B.6:1.54 C.1.5:4 D.3:2
2.《九章算术》中记载圆柱的体积计算方法是“周自乘,以高乘之,十二而一”,也就是“底面周长的平方乘高,再除以 12”。这种计算方法与现在的算法是一致的,只不过圆周率的近似值为3。一个圆柱体水桶底面周长为4分米,高为6分米。请用这种方法算出这个水桶最多可盛水( )升。(水桶的厚度忽略不计)
A.4 B.6 C.8 D.12
3.一个圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
4. 一个比例中,两内项的积是3,一个外项是0.75,另一外项是( )。
A.4 B.3 C. D.
5.x和y成正比例关系,当x=2时,y=;当x=5时,y=( )。
A. B. C.2 D.
6.下面各式中,表示x和y成反比例的是( )。
A.x+y=6 B.x=6+y C. D.y=6x
7.圆锥的高一定时,圆锥的体积和底面积( )。
A.成正比例 B.成反比例 C.不成比例 D.不能确定
8.下面各种关系中,成反比例关系的是( )。
A.三角形面积一定,它的底和高
B.圆的面积一定,它的半径平方与圆周率
C.速度一定时,行驶的路程和时间
D.平行四边形的高一定,它的面积和底
9.在圆周长公式C=πd中,如果C一定,那么π与d( )。
A.成反比例 B.不成比例 C.成正比例
10.下列说法中,两个量成反比例关系的有( )个。
①甲数的相当于乙数的,甲数和乙数。 ②比的前项一定,比的后项和比值。
③圆柱的体积一定,它的底面半径和高。 ④已知x、y是大于零的自然数,若,则x和y的关系。
A.1 B.2 C.3 D.4
二、判断题
11.一个圆柱与圆锥等底等高,圆柱的体积比圆锥多18m3,圆锥的体积是9m3。( )
12.一个圆锥的底面半径和高都扩大到原来的2倍,体积则扩大到原来的4倍。( )
13.比例5:3=15:9的内项3增加6,要使比例成立,外项9应该增加6。( )
14.如果ab=cd,那么a∶c=b∶d。( )
15.已知a,b是两个相关联的量,若(a,b均不为0),则a与b成正比例。( )
三、填空题
16.一个三位小数,用“四舍五入”法保留两位小数约是19.00,这个三位小数最小是 ,最大是 。
17.妈妈给小红的毛绒玩具网购了一个圆柱形透明收纳桶(如图),这个收纳桶的侧面积是 94.2dm2。这个收纳桶的底面积是 dm2;收纳桶的空间约是 dm3。
18.在一个比例里,两个内项的积是最小的质数,一个外项是5,另一个外项是 。
19.写出两个比值是 的比: 和 ,组成比例是: 。
20.a÷b=c(a,b,c均不为0),当c一定时,a和b成 ;当a一定时,b和c成 ;当b一定时,a和c成 。
21.如果4x-3y=0(y≠0),那么x和y成 比例关系。
22.水池的容积一定,水管每时的注水量和注满水池所需的时间成 比例。圆锥的体积一定,底面积和高成 比例。
23.冰雕艺术家有时会通过人工制作特色形状的冰块来进行冰雕雕刻。如果一名冰雕艺术家将相同质量的水倒入粗细不同的圆柱形水桶中,在一定条件下凝固成冰,则形成的冰底面积和高成 比例。
24.自行车前齿轮有48齿,后齿轮有16齿。当前齿轮转5圈时,后齿轮转 圈。
25.小明新买了一把弹簧秤,挂质量为3千克的苹果,弹簧长12.75厘米,挂质量为5千克的榴莲,弹簧长13.25厘米;如果挂质量为1千克的草莓,那么弹簧长 厘米。
四、计算题
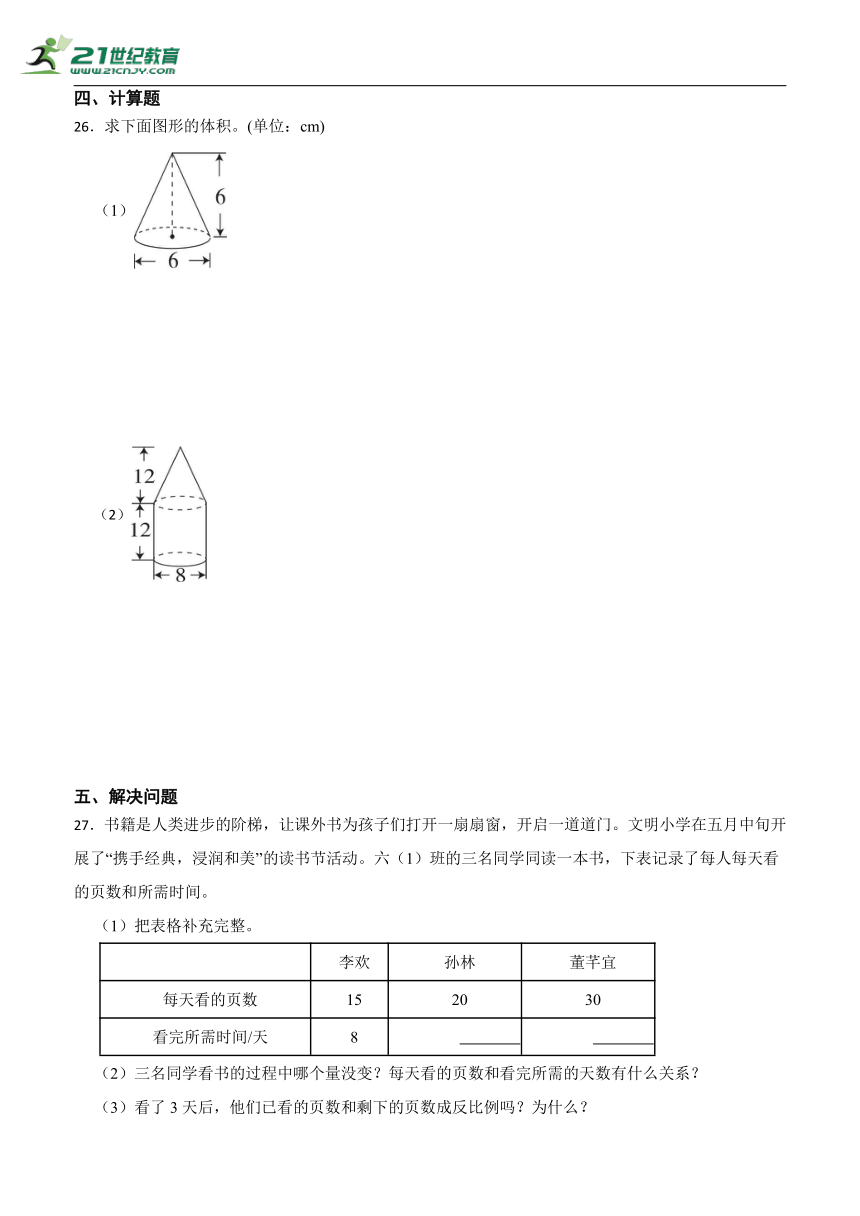
26.求下面图形的体积。(单位:cm)
(1)
五、解决问题
27.书籍是人类进步的阶梯,让课外书为孩子们打开一扇扇窗,开启一道道门。文明小学在五月中旬开展了“携手经典,浸润和美”的读书节活动。六(1)班的三名同学同读一本书,下表记录了每人每天看的页数和所需时间。
(1)把表格补充完整。
李欢 孙林 董芊宜
每天看的页数 15 20 30
看完所需时间/天 8
(2)三名同学看书的过程中哪个量没变?每天看的页数和看完所需的天数有什么关系?
(3)看了3天后,他们已看的页数和剩下的页数成反比例吗?为什么?
28.李军乘汽车去旅行,汽车的速度一定,路程与时间的关系如下表。
路程/千米 60 120 240 540 …
时间/时 1 2 4 6 …
(1)把上表填写完整。
(2)试着在下图中描出各点,并顺次连接起来。
(3)从(2)题中,你能发现行驶的路程与时间有什么关系吗?
(4)汽车行驶3.5时,行驶的路程是多少千米?
29.用如图所示的扇形纸片和圆形纸片能否制作成一个圆锥?请通过计算说明理由。
30.一个底面直径是2dm的圆柱形玻璃杯内盛有一些水,恰好占杯子容量的,现将一个铁块完全浸没在水中,水面上升了5cm,这时水面距杯口还有4 cm。这个杯子的容积是多少升?
31.如图,两个一样的圆柱,底面直径是4cm,高是6cm,按如图所示切开,切开后一个截面的面积分别是多少平方厘米?
答案解析部分
1.C
解:能组成比例的是:
3:8=1.5:4
故答案为:C。
比例的基本性质,在比例里,两个内项积等于两个外项积。
2.C
解:4×4×6÷12
=16×6÷12
=8(升)
故答案为:C。
圆柱的底面周长的平方×高÷ 12=圆柱的容积,据此解答。
3.D
解:3×3×3=27。
故答案为:D。
圆柱的体积=π×半径2×高,圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的3×3×3=27倍。
4.A
解:3÷0.75=4。
故答案为:A。
另一个外形=两个内项积÷一个外项。
5.D
解:x和y成正比例关系,说明x和y的比值相等;
2:=5:y
2y=×5
2y=
y=×
y=
故答案为:D。
正比例的判断方法:相关联,能变化,商一定。
6.C
解:
A、x+y=6,x与y和一定,不成比例关系;
B、x=6+y,得x-y=6,x与y差一定,不成比例关系;
C、,得xy=6,乘积一定,×反比例关系;
D、 y=6x,得到,商一定,成正比例关系。
故答案为:C。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
7.A
解:圆锥的体积与底面积是两种相关联的量,它们与圆锥的高有下面的关系:
圆锥的体积:底面积=圆锥的高(一定);已知圆锥的高一定,它的也是一定的,也就是圆锥的体积与底面积的比值一定,所以圆锥的体积与底面积成正比例。
故答案为:A。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
8.A
解:A、三角形面积一定,就是底和高的乘积一定,所以它的底和高成反比例关系,符合题意。
B、圆的面积和圆的半径不成比例,不符合题意。
C、平行四边形的高一定,就是面积和底的商一定,所以它的面积和底成正比例关系,不符合题意。
D、速度一定,就是路程和时间的商一定,所以行驶的路程和时间成正比例关系,不符合题意。
故答案为:A。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
9.B
解:π是定量,C一定时,两个定量,一个变量,不符合比例关系概念,π与d不成比例。
故答案为:B。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
10.B
解:①由甲数×=乙数×,得到=,甲数与乙数成正比例关系;
②比的前项=后项×比值,前项一定,比的后项和比值成反比例;
③根据V=πr2×h,一个圆柱的体积一定,底面积和高成反比例,底面半径和高不成反比例;
④由,得xy=6,x与y成反比关系;
两个量成反比例关系的有②④,2个。
故答案为:B。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
11.正确
解:圆锥的体积:18÷2=9( m3 ),
圆柱的体积是:9×3=27( m3 )
故答案为:正确。
等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱的体积比圆锥的体积多2倍,由此即可解答。
12.错误
解:2×2×2=8倍,体积扩大到原来的8倍。原题错误。
故答案为:错误。
根据积的变化规律可知,底面半径扩大2倍,体积扩大4倍。高扩大2倍,体积扩大2倍。底面半径和高同时扩大2倍,体积扩大8倍。
13.错误
解:3+6=9;
9×15÷5
=135÷5
=27
27-9=16,所以外项应该增加16。
故答案为:错误。
内项3+6=9,根据比例的基本性质,两内项的积等于两外项的积,所以外项等于9×15÷5=27,27-9=16,据此解答。
14.错误
解:如果ab=cd,那么a∶c=d:b
故答案为:错误。
比例的基本性质,在比例里,两个内项积等于两个外项积。
15.错误
解:由,得ab=1.5,乘积一定,成反比例关系;原题说法错误。
故答案为:错误。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
16.18.995;19.004
17.28.26;141.3
解:94.2÷5=18.84(分米)
18.84÷3.14÷2=3(分米)
3.14×3×3=28.26(平方分米)
28.26×5=141.3(立方分米)
故答案为:28.26;141.3。
侧面积÷高=底面周长,底面周长÷π÷2=底面半径,π×底面半径的平方=底面积,底面积×高=体积。
18.0.4
解:2÷5=0.4
故答案为:0.4。
最小的质数是2,根据比例的基本性质:内项积等于外项积进行解答即可。
19.5:2;10:4;5:2 =10:4(答案不唯一)
解:这两个比是5:2和10:4;组成的比例是:5:2=10:4。
故答案为5:2;10:4;:5:2=10:4。
比和分数的关系中,比的前项相当于分数的分子,后项相当于分数的分母;
比的前项和后项同时乘或除以相同的数(0除外),比值不变;
组成比例的两个比的比值相等。
20.正比例;反比例;正比例
解:由a÷b=c,c一定也就是商一定,a和b成正比例,当a一定时,a=bc,乘积一定b和c成反比例;b=a÷c,当b一定时,商一定a和c成正比例。
故答案为:正比例;反比例;正比例。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
21.正
解:由4x-3y=0,得, x和y比值一定,成正比例关系。
故答案为:正。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
22.反;反
解:水池的容积一定,水管每小时注水量×所用时间=水池的容积(一定),故水管每小时注水量和所用时间成反比例;
因为圆锥的底面积×圆锥的高=圆锥的体积×3(一定),所以圆锥的体积一定,底面积和高成反比例关系。
故答案为:反;反。
两种相关联的量,若它们的比值一定,两种量成正比例关系;若它们的乘积一定,两种量成反比例关系。
23.反
解:底面积×高=体积(一定),所以,形成的冰底面积和高成反比例。
故答案为:反。
乘积一定的两个量成反比例关系。水的质量相同,说明体积相等。圆柱体积=底面积×高,据此解题。
24.15
解:设后齿轮转动x圈。
16x=48×5
16x=240
x=15
故答案为:15。
前轮与后轮走过的路程是一定的,齿轮的齿数与转过的圈数成反比例,根据乘积一定,设出未知数,列出比例式;解答即可。
25.12.25
解:(13.25-12.75)÷(5-3)
=0.5÷2
=0.25(厘米)
12.75-0.25×(3-1)
=12.75-0.5
=12.25(厘米)。
故答案为:12.25。
先求出每增加1千克的质量,弹簧的长度伸长的长度;再用12.75减去这个数即可。
26.(1)解:(6÷2)2×3.14×6×
=9×3.14×2
=28.26×2
=56.52(cm3);
答:图形的体积为56.52cm3。
(2)解:(8÷2)2×3.14×12×+(8÷2)2×3.14×12
=16×3.14×4+16×3.14×12
=200.96+602.88
=803.84(cm3);
答:图形的体积为56.52cm3。
(1)圆锥的体积计算公式为,据此求解;
(2)圆柱的体积计算公式为,该图形的体积=圆柱的体积+圆锥的体积,据此求解。
27.(1)6;4
(2)解:每天看的页数×看完需要的天数=书的总页数(一定)
答:三名同学看书的过程中,书的总页数不变。每天看的页数和看完所需的天数成反比例关系。
(3)答:看了3天后,他们已看的页数和剩下的页数不成反比例。因为已看的页数+剩下的页数=书总页数(一定),和是一定的,但积不一定。
(1)15×8=120(页)
120÷20=6(天)
120÷30=4(天)
故答案为:6;4。
(1)根据三名同学同读一本书,可知总页数相同,每天看的页数×看完的时间=总页数,看完的时间=总页数÷每天看的页数;
(2)(3)由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
28.(1)解:填表如下:
路程/千米 60 120 240 360 540 …
时间/时 1 2 4 6 9 …
(2)
(3)答:观察图像,发现行驶的路程与时间成正比例关系。
(4)解:60×3.5=210(千米)
答:行驶的路程是210千米。
解:(1)60÷1=60(千米/小时)
60×6=360(千米)
540÷60=9(小时)
故答案为:360;9。
(1)根据路程=速度×时间,时间=路程÷速度,代入数据计算即可;
(2)图中横轴是时间,纵轴是路程,对照表格数据描点连线即可;
(3)结合图形特征,正比例图像是一条直线,并且速度一定,路程与时间×正比例关系;
(4)根据路程=速度×时间,代入数据计算即可。
29.解:扇形圆弧的长:3.14 ×2×2×=9.42( cm)
圆的周长:3.14 ×3 =9.42(cm)
答:扇形圆弧的长和圆的周长相等,所以能制作成一个圆锥。
要想题目给的纸片能够制作成一个圆锥,只需要扇形纸片圆弧部分长度和圆形纸片的周长相等。可以分别计算扇形纸片的圆弧部分长度和圆形纸片的周长;若相等,则可以组成圆锥;若不相等,则不可以组成圆锥。
30.解:2dm=20cm
3.14×(20÷2)2×(5+4)÷(1-)
=3.14×100×9÷
=314×9÷
=2826÷
=4710(cm3)
4710 cm3=4.71L
答:这个杯子的容积是4.71L。
先把单位进行换算,即2dm=20cm,原来杯子中的水到杯口的距离=铁块完全浸没在水中水上升的高度+放入铁块后水面距杯口的距离,那么杯子的高=原来杯子中的水到杯口的距离÷(1-原来水占杯子容量的几分之几),所以这个杯子的容积=π×(直径÷2)2×高,据此作答即可。
31.解:4×6=24(cm2)
3.14×(4÷2)2
=3.14×4
=12.56(cm2)
答:切开后一个截面的面积分别是24cm2、12.56cm2。
观察图,竖着切,截面是一个长方形,长是圆柱的高,宽是圆柱的底面直径;横着切,截面和圆柱的底面相同,直径是4cm,根据圆的面积公式计算即可。
一、单选题
1.下面的比中能与3:8组成比例的是( )。
A.3.5:6 B.6:1.54 C.1.5:4 D.3:2
2.《九章算术》中记载圆柱的体积计算方法是“周自乘,以高乘之,十二而一”,也就是“底面周长的平方乘高,再除以 12”。这种计算方法与现在的算法是一致的,只不过圆周率的近似值为3。一个圆柱体水桶底面周长为4分米,高为6分米。请用这种方法算出这个水桶最多可盛水( )升。(水桶的厚度忽略不计)
A.4 B.6 C.8 D.12
3.一个圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
4. 一个比例中,两内项的积是3,一个外项是0.75,另一外项是( )。
A.4 B.3 C. D.
5.x和y成正比例关系,当x=2时,y=;当x=5时,y=( )。
A. B. C.2 D.
6.下面各式中,表示x和y成反比例的是( )。
A.x+y=6 B.x=6+y C. D.y=6x
7.圆锥的高一定时,圆锥的体积和底面积( )。
A.成正比例 B.成反比例 C.不成比例 D.不能确定
8.下面各种关系中,成反比例关系的是( )。
A.三角形面积一定,它的底和高
B.圆的面积一定,它的半径平方与圆周率
C.速度一定时,行驶的路程和时间
D.平行四边形的高一定,它的面积和底
9.在圆周长公式C=πd中,如果C一定,那么π与d( )。
A.成反比例 B.不成比例 C.成正比例
10.下列说法中,两个量成反比例关系的有( )个。
①甲数的相当于乙数的,甲数和乙数。 ②比的前项一定,比的后项和比值。
③圆柱的体积一定,它的底面半径和高。 ④已知x、y是大于零的自然数,若,则x和y的关系。
A.1 B.2 C.3 D.4
二、判断题
11.一个圆柱与圆锥等底等高,圆柱的体积比圆锥多18m3,圆锥的体积是9m3。( )
12.一个圆锥的底面半径和高都扩大到原来的2倍,体积则扩大到原来的4倍。( )
13.比例5:3=15:9的内项3增加6,要使比例成立,外项9应该增加6。( )
14.如果ab=cd,那么a∶c=b∶d。( )
15.已知a,b是两个相关联的量,若(a,b均不为0),则a与b成正比例。( )
三、填空题
16.一个三位小数,用“四舍五入”法保留两位小数约是19.00,这个三位小数最小是 ,最大是 。
17.妈妈给小红的毛绒玩具网购了一个圆柱形透明收纳桶(如图),这个收纳桶的侧面积是 94.2dm2。这个收纳桶的底面积是 dm2;收纳桶的空间约是 dm3。
18.在一个比例里,两个内项的积是最小的质数,一个外项是5,另一个外项是 。
19.写出两个比值是 的比: 和 ,组成比例是: 。
20.a÷b=c(a,b,c均不为0),当c一定时,a和b成 ;当a一定时,b和c成 ;当b一定时,a和c成 。
21.如果4x-3y=0(y≠0),那么x和y成 比例关系。
22.水池的容积一定,水管每时的注水量和注满水池所需的时间成 比例。圆锥的体积一定,底面积和高成 比例。
23.冰雕艺术家有时会通过人工制作特色形状的冰块来进行冰雕雕刻。如果一名冰雕艺术家将相同质量的水倒入粗细不同的圆柱形水桶中,在一定条件下凝固成冰,则形成的冰底面积和高成 比例。
24.自行车前齿轮有48齿,后齿轮有16齿。当前齿轮转5圈时,后齿轮转 圈。
25.小明新买了一把弹簧秤,挂质量为3千克的苹果,弹簧长12.75厘米,挂质量为5千克的榴莲,弹簧长13.25厘米;如果挂质量为1千克的草莓,那么弹簧长 厘米。
四、计算题
26.求下面图形的体积。(单位:cm)
(1)
五、解决问题
27.书籍是人类进步的阶梯,让课外书为孩子们打开一扇扇窗,开启一道道门。文明小学在五月中旬开展了“携手经典,浸润和美”的读书节活动。六(1)班的三名同学同读一本书,下表记录了每人每天看的页数和所需时间。
(1)把表格补充完整。
李欢 孙林 董芊宜
每天看的页数 15 20 30
看完所需时间/天 8
(2)三名同学看书的过程中哪个量没变?每天看的页数和看完所需的天数有什么关系?
(3)看了3天后,他们已看的页数和剩下的页数成反比例吗?为什么?
28.李军乘汽车去旅行,汽车的速度一定,路程与时间的关系如下表。
路程/千米 60 120 240 540 …
时间/时 1 2 4 6 …
(1)把上表填写完整。
(2)试着在下图中描出各点,并顺次连接起来。
(3)从(2)题中,你能发现行驶的路程与时间有什么关系吗?
(4)汽车行驶3.5时,行驶的路程是多少千米?
29.用如图所示的扇形纸片和圆形纸片能否制作成一个圆锥?请通过计算说明理由。
30.一个底面直径是2dm的圆柱形玻璃杯内盛有一些水,恰好占杯子容量的,现将一个铁块完全浸没在水中,水面上升了5cm,这时水面距杯口还有4 cm。这个杯子的容积是多少升?
31.如图,两个一样的圆柱,底面直径是4cm,高是6cm,按如图所示切开,切开后一个截面的面积分别是多少平方厘米?
答案解析部分
1.C
解:能组成比例的是:
3:8=1.5:4
故答案为:C。
比例的基本性质,在比例里,两个内项积等于两个外项积。
2.C
解:4×4×6÷12
=16×6÷12
=8(升)
故答案为:C。
圆柱的底面周长的平方×高÷ 12=圆柱的容积,据此解答。
3.D
解:3×3×3=27。
故答案为:D。
圆柱的体积=π×半径2×高,圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的3×3×3=27倍。
4.A
解:3÷0.75=4。
故答案为:A。
另一个外形=两个内项积÷一个外项。
5.D
解:x和y成正比例关系,说明x和y的比值相等;
2:=5:y
2y=×5
2y=
y=×
y=
故答案为:D。
正比例的判断方法:相关联,能变化,商一定。
6.C
解:
A、x+y=6,x与y和一定,不成比例关系;
B、x=6+y,得x-y=6,x与y差一定,不成比例关系;
C、,得xy=6,乘积一定,×反比例关系;
D、 y=6x,得到,商一定,成正比例关系。
故答案为:C。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
7.A
解:圆锥的体积与底面积是两种相关联的量,它们与圆锥的高有下面的关系:
圆锥的体积:底面积=圆锥的高(一定);已知圆锥的高一定,它的也是一定的,也就是圆锥的体积与底面积的比值一定,所以圆锥的体积与底面积成正比例。
故答案为:A。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
8.A
解:A、三角形面积一定,就是底和高的乘积一定,所以它的底和高成反比例关系,符合题意。
B、圆的面积和圆的半径不成比例,不符合题意。
C、平行四边形的高一定,就是面积和底的商一定,所以它的面积和底成正比例关系,不符合题意。
D、速度一定,就是路程和时间的商一定,所以行驶的路程和时间成正比例关系,不符合题意。
故答案为:A。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
9.B
解:π是定量,C一定时,两个定量,一个变量,不符合比例关系概念,π与d不成比例。
故答案为:B。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
10.B
解:①由甲数×=乙数×,得到=,甲数与乙数成正比例关系;
②比的前项=后项×比值,前项一定,比的后项和比值成反比例;
③根据V=πr2×h,一个圆柱的体积一定,底面积和高成反比例,底面半径和高不成反比例;
④由,得xy=6,x与y成反比关系;
两个量成反比例关系的有②④,2个。
故答案为:B。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
11.正确
解:圆锥的体积:18÷2=9( m3 ),
圆柱的体积是:9×3=27( m3 )
故答案为:正确。
等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱的体积比圆锥的体积多2倍,由此即可解答。
12.错误
解:2×2×2=8倍,体积扩大到原来的8倍。原题错误。
故答案为:错误。
根据积的变化规律可知,底面半径扩大2倍,体积扩大4倍。高扩大2倍,体积扩大2倍。底面半径和高同时扩大2倍,体积扩大8倍。
13.错误
解:3+6=9;
9×15÷5
=135÷5
=27
27-9=16,所以外项应该增加16。
故答案为:错误。
内项3+6=9,根据比例的基本性质,两内项的积等于两外项的积,所以外项等于9×15÷5=27,27-9=16,据此解答。
14.错误
解:如果ab=cd,那么a∶c=d:b
故答案为:错误。
比例的基本性质,在比例里,两个内项积等于两个外项积。
15.错误
解:由,得ab=1.5,乘积一定,成反比例关系;原题说法错误。
故答案为:错误。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
16.18.995;19.004
17.28.26;141.3
解:94.2÷5=18.84(分米)
18.84÷3.14÷2=3(分米)
3.14×3×3=28.26(平方分米)
28.26×5=141.3(立方分米)
故答案为:28.26;141.3。
侧面积÷高=底面周长,底面周长÷π÷2=底面半径,π×底面半径的平方=底面积,底面积×高=体积。
18.0.4
解:2÷5=0.4
故答案为:0.4。
最小的质数是2,根据比例的基本性质:内项积等于外项积进行解答即可。
19.5:2;10:4;5:2 =10:4(答案不唯一)
解:这两个比是5:2和10:4;组成的比例是:5:2=10:4。
故答案为5:2;10:4;:5:2=10:4。
比和分数的关系中,比的前项相当于分数的分子,后项相当于分数的分母;
比的前项和后项同时乘或除以相同的数(0除外),比值不变;
组成比例的两个比的比值相等。
20.正比例;反比例;正比例
解:由a÷b=c,c一定也就是商一定,a和b成正比例,当a一定时,a=bc,乘积一定b和c成反比例;b=a÷c,当b一定时,商一定a和c成正比例。
故答案为:正比例;反比例;正比例。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
21.正
解:由4x-3y=0,得, x和y比值一定,成正比例关系。
故答案为:正。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
22.反;反
解:水池的容积一定,水管每小时注水量×所用时间=水池的容积(一定),故水管每小时注水量和所用时间成反比例;
因为圆锥的底面积×圆锥的高=圆锥的体积×3(一定),所以圆锥的体积一定,底面积和高成反比例关系。
故答案为:反;反。
两种相关联的量,若它们的比值一定,两种量成正比例关系;若它们的乘积一定,两种量成反比例关系。
23.反
解:底面积×高=体积(一定),所以,形成的冰底面积和高成反比例。
故答案为:反。
乘积一定的两个量成反比例关系。水的质量相同,说明体积相等。圆柱体积=底面积×高,据此解题。
24.15
解:设后齿轮转动x圈。
16x=48×5
16x=240
x=15
故答案为:15。
前轮与后轮走过的路程是一定的,齿轮的齿数与转过的圈数成反比例,根据乘积一定,设出未知数,列出比例式;解答即可。
25.12.25
解:(13.25-12.75)÷(5-3)
=0.5÷2
=0.25(厘米)
12.75-0.25×(3-1)
=12.75-0.5
=12.25(厘米)。
故答案为:12.25。
先求出每增加1千克的质量,弹簧的长度伸长的长度;再用12.75减去这个数即可。
26.(1)解:(6÷2)2×3.14×6×
=9×3.14×2
=28.26×2
=56.52(cm3);
答:图形的体积为56.52cm3。
(2)解:(8÷2)2×3.14×12×+(8÷2)2×3.14×12
=16×3.14×4+16×3.14×12
=200.96+602.88
=803.84(cm3);
答:图形的体积为56.52cm3。
(1)圆锥的体积计算公式为,据此求解;
(2)圆柱的体积计算公式为,该图形的体积=圆柱的体积+圆锥的体积,据此求解。
27.(1)6;4
(2)解:每天看的页数×看完需要的天数=书的总页数(一定)
答:三名同学看书的过程中,书的总页数不变。每天看的页数和看完所需的天数成反比例关系。
(3)答:看了3天后,他们已看的页数和剩下的页数不成反比例。因为已看的页数+剩下的页数=书总页数(一定),和是一定的,但积不一定。
(1)15×8=120(页)
120÷20=6(天)
120÷30=4(天)
故答案为:6;4。
(1)根据三名同学同读一本书,可知总页数相同,每天看的页数×看完的时间=总页数,看完的时间=总页数÷每天看的页数;
(2)(3)由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
28.(1)解:填表如下:
路程/千米 60 120 240 360 540 …
时间/时 1 2 4 6 9 …
(2)
(3)答:观察图像,发现行驶的路程与时间成正比例关系。
(4)解:60×3.5=210(千米)
答:行驶的路程是210千米。
解:(1)60÷1=60(千米/小时)
60×6=360(千米)
540÷60=9(小时)
故答案为:360;9。
(1)根据路程=速度×时间,时间=路程÷速度,代入数据计算即可;
(2)图中横轴是时间,纵轴是路程,对照表格数据描点连线即可;
(3)结合图形特征,正比例图像是一条直线,并且速度一定,路程与时间×正比例关系;
(4)根据路程=速度×时间,代入数据计算即可。
29.解:扇形圆弧的长:3.14 ×2×2×=9.42( cm)
圆的周长:3.14 ×3 =9.42(cm)
答:扇形圆弧的长和圆的周长相等,所以能制作成一个圆锥。
要想题目给的纸片能够制作成一个圆锥,只需要扇形纸片圆弧部分长度和圆形纸片的周长相等。可以分别计算扇形纸片的圆弧部分长度和圆形纸片的周长;若相等,则可以组成圆锥;若不相等,则不可以组成圆锥。
30.解:2dm=20cm
3.14×(20÷2)2×(5+4)÷(1-)
=3.14×100×9÷
=314×9÷
=2826÷
=4710(cm3)
4710 cm3=4.71L
答:这个杯子的容积是4.71L。
先把单位进行换算,即2dm=20cm,原来杯子中的水到杯口的距离=铁块完全浸没在水中水上升的高度+放入铁块后水面距杯口的距离,那么杯子的高=原来杯子中的水到杯口的距离÷(1-原来水占杯子容量的几分之几),所以这个杯子的容积=π×(直径÷2)2×高,据此作答即可。
31.解:4×6=24(cm2)
3.14×(4÷2)2
=3.14×4
=12.56(cm2)
答:切开后一个截面的面积分别是24cm2、12.56cm2。
观察图,竖着切,截面是一个长方形,长是圆柱的高,宽是圆柱的底面直径;横着切,截面和圆柱的底面相同,直径是4cm,根据圆的面积公式计算即可。
同课章节目录
- 一 比例
- 1、比例的意义与性质
- 2、正比例(一)
- 3、解比例
- 4、正比例(二)
- 5、正比例应用问题
- 6、反比例(一)
- 7、反比例(二)
- 8、反比例应用问题
- 二 比例尺
- 9、认识比例尺
- 10、比例尺的应用
- 11、方向与位置
- 四 圆柱与圆锥
- 16、圆柱与圆锥的认识
- 17、圆柱的表面积
- 18、圆柱的体积
- 19、圆锥的体积
- 五 整理与复习
- 20、整数与小数
- 21、数的整除
- 22、分数与百分数
- 23、加减运算
- 24、乘除运算
- 25、四则混合运算
- 26、代数式与方程
- 27、比与比例
- 28、应用问题
- 29、线与角
- 30、方向与位置
- 31、位置的确定
- 32、平面图形
- 33、图形的交换
- 34、立体图形
- 35、数据的整理
- 36、统计与可能性
- 总复习
