8.3.1 棱柱、棱锥、棱台的表面积和体积 同步巩固练 2024-2025学年数学人教A版(2019) 必修第二册
文档属性
| 名称 | 8.3.1 棱柱、棱锥、棱台的表面积和体积 同步巩固练 2024-2025学年数学人教A版(2019) 必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 13:56:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
8.3.1 棱柱、棱锥、棱台的表面积和体积 同步巩固练
2024-2025学年数学人教A版(2019) 必修第二册
一、单选题
1.已知棱长为2,各面均为等边三角形的四面体,则其表面积为( )
A.12 B. C. D.
2.某几何体为棱柱或棱锥,且每个面均为边长是2的正三角形或正方形,给出下面4个值:①;②24;③;④.则该几何体的表面积可能是其中的( )
A.①②③ B.①③④ C.①②④ D.①②③④
3.四棱台的两底面分别是边长为和的正方形,各侧棱长都相等,高为,且侧面积等于两底面积之和,则下列关系式中正确的是( )
A. B. C. D.
4.如图1所示,宫灯又称宫廷花灯,是中国彩灯中富有特色的汉民族传统手工艺品之一.图2是小明为自家设计的一个花灯的直观图,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为和,正六棱台与正六棱柱的高分别为和,则该花灯的表面积为( )
A. B.
C. D.
5.已知正三棱台的上、下底面边长分别为4和6,斜高为1,则该正三棱台的体积为( )
A. B. C. D.
6.已知正四棱锥的底面边长是,体积是,那么这个四棱锥的侧棱长为( )
A. B.2 C. D.
7.如图,在多面体中,四边形为矩形,,,,,到平面的距离为3,则多面体的体积为( )
A.18 B.15 C.12 D.9
8.学校以“布一室馨香,育满园桃李”为主题开展了系列评比活动,动员师生一起为营造舒心愉悦的学习生活环境奉献智慧.张老师特地培育了一盆绿萝放置在教室内,绿萝底部的盆近似看成一个圆台,圆台的上、下底面半径之比为,母线长为,其母线与底面所成的角为,则这个圆台的体积为( )
A. B.
C. D.
二、填空题
9.若正三棱柱的所有棱长均为,且其侧面积为12,则 .
10.如图,在正四棱台中,已知,,且棱台的侧面积为6,则该棱台的高为 .
11.棱长为1的正方体纸盒展开后如图所示,则在原正方体纸盒上,分别将四点两两相连,构成的几何体的表面积为 .
12.已知侧棱长为5,高为4的正四棱锥被平行于底面的平面所截,截去一个高为2的正四棱锥,所得的棱台的体积为 .
13.在棱长为的正方体中,点是棱靠近的三等分点,点是棱靠近的四等分点,则三棱锥的体积为
14.“升”是我国古代测量粮食的一种容器,在“升”装满后用手指成筷子沿升口刮平,这叫“平升”,如图所示的“升”,从内部测量,其上、下底面均为正方形,边长分别为和,侧面是全等的等腰梯形,梯形的高为,那么这个“升”的“平升”可以装 mL的粮食.(结果保留整数)
三、解答题
15.正四棱锥S﹣ABCD的底面边长为4,高为1,求:
(1)求棱锥的侧棱长和斜高;
(2)求棱锥的表面积.
16.已知长方体中,,求:
(1)长方体表面积;
(2)三棱锥的体积.
17.已知正四棱锥的侧面积是底面积的2倍,且高为3.
(1)求它的表面积;
(2)求它的体积.
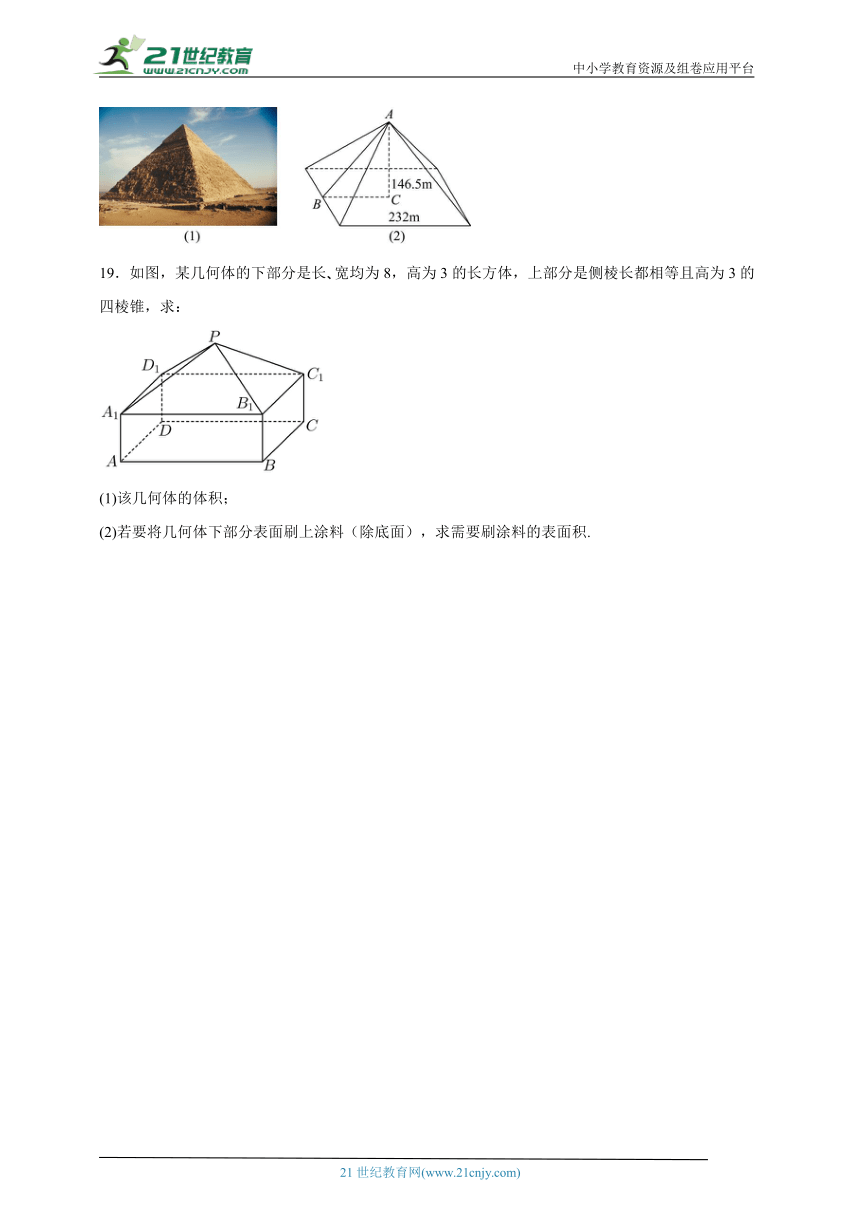
18.如图(1),埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.已知该金字塔高约146.5m,底面边长约232m,求这座金字塔的侧面积和体积(分别精确到和).
19.如图,某几何体的下部分是长 宽均为8,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求:
(1)该几何体的体积;
(2)若要将几何体下部分表面刷上涂料(除底面),求需要刷涂料的表面积.
参考答案
1.C
利用三角形面积公式及四面体表面积的意义计算即得.
棱长为2,各面均为等边三角形的四面体,
其表面积为:.
故选:C
2.D
当该几何体为正四面体时,其表面积为.
当该几何体为正四棱锥时,其表面积为.
当该几何体为正三棱柱时,其表面积为.
当该几何体为正方体时,其表面积为.
故选:D.
3.C
解:由题意可知,该四棱台为正四棱台,如图:过顶点作底面于,由正四棱台的特征可知,在底面对角线上,根据四边形为等腰梯形,所以,
过 作,连接,则,
由于底面,底面,所以,又,平面,
所以平面, 平面, 故 ,因此是侧面梯形的高,
设侧面梯形的高为,所以 ,
,消去得,
∴,可得,
∴.
故选:C.
4.A
正六棱柱的六个侧面面积之和为,
正六棱柱的底面面积为,
如图所示,正六棱台中,,
过点分别作垂直于底面于点,
连接相交于点,则分别为的中点,
过点作⊥于点,连接,则为正六棱台的斜高,
其中,,,
由勾股定理得,故,
所以正六棱台的斜高为,
故正六棱台的侧面积为,
又正六棱台的下底面面积为,
所以该花灯的表面积为.
故选:A.
5.D
利用已知条件算出上下底面的面积和棱台的高,再由体积公式计算.
由正三棱台的结构特征知,其上、下底面分别是边长为4和6的等边三角形,如图所示,
为两底面的中心,则为的中点,过作下底面垂线,垂足为,
,,,
棱台的高,
该正三棱台的上底面的面积为,下底面的面积为,
所以正三棱台的体积.
故选:D
6.C
由题意首先求出正四棱锥的高,再求出底面对角线长度的一半,最后由勾股定理即可得解.
设四棱锥的高为,根据已知条件可得,所以,
而,所以这个四棱锥的侧棱长为.
故选:C.
7.B
将多面体补形为三棱柱,过点F作平面平面与直线AB,DC分别交于点P,Q,且满足,利用,进行计算即可.
如图,可将多面体补形为三棱柱,
过点F作平面平面与直线AB,DC分别交于点P,Q,
且满足,由题知,
易知平面FPQ,∴,
连接EB,EC,则,∴.
故选:
8.A
如图所示:
过点作与点,不妨设上下底面圆圆心分别为,半径分别为,圆台的高,
由题意母线长为,其母线与底面所成的角为,即,
从而,,
又圆台的上、下底面半径之比为,即,
所以,圆台上下两个底面的面积分别为,
由圆台体积公式可知.
故选:A.
9.2
根据三棱柱侧面积公式即可求解.
因为正三棱柱的所有棱长均为,所以三棱柱的侧面是边长为的正方形,
所以侧面积,所以.
故答案为:2
10.
首先根据正棱台的侧面积得到斜高为1,再计算正棱台的高即可.
如图所示:
设正四棱台的侧高为,高为,
棱台的侧面积,所以.
所以.
故答案为:
11.
在原正方体纸盒上,分别将四点两两相连,如图所示,
因为为正方体的面对角线,
所以,
所以为正四面体,
所以表面积为:,
故答案为:.
12.21
如图正四棱锥,其中底面于,
侧棱,高,所以,
所以下底面边长,
因为平面平行于底面,且,,
所以在与相似,且,
所以,
则正方形面积,正方形面积,
所得的棱台体积为.
故答案为:21
13./0.125
根据锥体体积公式即可求解.
由于平面,
所以,
故答案为:
14.1167
根据题意画出正四棱台的直观图,其中底面是边长为20cm的正方形,底面是边长为10cm的正方形,侧面等腰梯形的高cm,记底面ABCD和底面的中心分别为与,则是正四棱台的高,
过作平面的垂线,垂足为,则,且,,
则,,
则,
侧面是等腰梯形,
,则,
则棱台的高,
则由棱台的体积公式得mL,
故答案为:1167.
15.(1)侧棱长为3,斜高为
(2)
(1)设SO为正四棱锥S﹣ABCD的高,则SO=1,作OM⊥BC,则M为BC 中点,连接OM,OB,则SO⊥OB,SO⊥OM,由此能求出棱锥的侧棱长和斜高.
(2)棱锥的表面积,由此能求出结果.
(1)设SO为正四棱锥S﹣ABCD的高,则SO=1,
作OM⊥BC于M,则M为BC 中点,
连接OM,OB,则SO⊥OB,SO⊥OM,
BC=4,BM=2,则OM=2,OB=,
在Rt△SOB中,,
在Rt△SOM中,,
∴棱锥的侧棱长为3,斜高为.
(2)棱锥的表面积:
.
16.(1)10;
(2).
(1)利用长方体的表面积公式计算即得.
(2)利用锥体体积公式计算即得.
(1)长方体中,,,
因此长方体的侧面积,
所以长方体的表面积.
(2)的面积,
显然三棱锥的高为,
所以三棱锥的体积.
17.(1)36
(2)12
(1)画出图形,设对应的边长,再根据侧面积是底面积的2倍列出对应的方程求解棱长,再计算表面积即可;
(2)利用锥体体积公式求解.
(1)如图,设,是斜高,
,,.
在中,,,,
.,,.
(2)正四棱锥的体积.
18.侧面积约为,体积约为
根据棱锥的侧面积公式和体积公式结合已知条件求解即可
根据题意可抽象出图(2),其中AC为高,则,,底面周长.
.
.
因此,这座金字塔的侧面积约为,体积约为.
19.(1)256
(2)96
(1)求出长方体的体积和四棱锥体积,相加后得到答案;
(2)求出几何体下部分侧面积,得到答案.
(1)长方体的体积为,四棱锥的体积为,
故该几何体的体积为;
(2)长方体侧面面积为,
故要将几何体下部分表面刷上涂料(除底面),需要刷涂料的表面积为96.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
8.3.1 棱柱、棱锥、棱台的表面积和体积 同步巩固练
2024-2025学年数学人教A版(2019) 必修第二册
一、单选题
1.已知棱长为2,各面均为等边三角形的四面体,则其表面积为( )
A.12 B. C. D.
2.某几何体为棱柱或棱锥,且每个面均为边长是2的正三角形或正方形,给出下面4个值:①;②24;③;④.则该几何体的表面积可能是其中的( )
A.①②③ B.①③④ C.①②④ D.①②③④
3.四棱台的两底面分别是边长为和的正方形,各侧棱长都相等,高为,且侧面积等于两底面积之和,则下列关系式中正确的是( )
A. B. C. D.
4.如图1所示,宫灯又称宫廷花灯,是中国彩灯中富有特色的汉民族传统手工艺品之一.图2是小明为自家设计的一个花灯的直观图,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为和,正六棱台与正六棱柱的高分别为和,则该花灯的表面积为( )
A. B.
C. D.
5.已知正三棱台的上、下底面边长分别为4和6,斜高为1,则该正三棱台的体积为( )
A. B. C. D.
6.已知正四棱锥的底面边长是,体积是,那么这个四棱锥的侧棱长为( )
A. B.2 C. D.
7.如图,在多面体中,四边形为矩形,,,,,到平面的距离为3,则多面体的体积为( )
A.18 B.15 C.12 D.9
8.学校以“布一室馨香,育满园桃李”为主题开展了系列评比活动,动员师生一起为营造舒心愉悦的学习生活环境奉献智慧.张老师特地培育了一盆绿萝放置在教室内,绿萝底部的盆近似看成一个圆台,圆台的上、下底面半径之比为,母线长为,其母线与底面所成的角为,则这个圆台的体积为( )
A. B.
C. D.
二、填空题
9.若正三棱柱的所有棱长均为,且其侧面积为12,则 .
10.如图,在正四棱台中,已知,,且棱台的侧面积为6,则该棱台的高为 .
11.棱长为1的正方体纸盒展开后如图所示,则在原正方体纸盒上,分别将四点两两相连,构成的几何体的表面积为 .
12.已知侧棱长为5,高为4的正四棱锥被平行于底面的平面所截,截去一个高为2的正四棱锥,所得的棱台的体积为 .
13.在棱长为的正方体中,点是棱靠近的三等分点,点是棱靠近的四等分点,则三棱锥的体积为
14.“升”是我国古代测量粮食的一种容器,在“升”装满后用手指成筷子沿升口刮平,这叫“平升”,如图所示的“升”,从内部测量,其上、下底面均为正方形,边长分别为和,侧面是全等的等腰梯形,梯形的高为,那么这个“升”的“平升”可以装 mL的粮食.(结果保留整数)
三、解答题
15.正四棱锥S﹣ABCD的底面边长为4,高为1,求:
(1)求棱锥的侧棱长和斜高;
(2)求棱锥的表面积.
16.已知长方体中,,求:
(1)长方体表面积;
(2)三棱锥的体积.
17.已知正四棱锥的侧面积是底面积的2倍,且高为3.
(1)求它的表面积;
(2)求它的体积.
18.如图(1),埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.已知该金字塔高约146.5m,底面边长约232m,求这座金字塔的侧面积和体积(分别精确到和).
19.如图,某几何体的下部分是长 宽均为8,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求:
(1)该几何体的体积;
(2)若要将几何体下部分表面刷上涂料(除底面),求需要刷涂料的表面积.
参考答案
1.C
利用三角形面积公式及四面体表面积的意义计算即得.
棱长为2,各面均为等边三角形的四面体,
其表面积为:.
故选:C
2.D
当该几何体为正四面体时,其表面积为.
当该几何体为正四棱锥时,其表面积为.
当该几何体为正三棱柱时,其表面积为.
当该几何体为正方体时,其表面积为.
故选:D.
3.C
解:由题意可知,该四棱台为正四棱台,如图:过顶点作底面于,由正四棱台的特征可知,在底面对角线上,根据四边形为等腰梯形,所以,
过 作,连接,则,
由于底面,底面,所以,又,平面,
所以平面, 平面, 故 ,因此是侧面梯形的高,
设侧面梯形的高为,所以 ,
,消去得,
∴,可得,
∴.
故选:C.
4.A
正六棱柱的六个侧面面积之和为,
正六棱柱的底面面积为,
如图所示,正六棱台中,,
过点分别作垂直于底面于点,
连接相交于点,则分别为的中点,
过点作⊥于点,连接,则为正六棱台的斜高,
其中,,,
由勾股定理得,故,
所以正六棱台的斜高为,
故正六棱台的侧面积为,
又正六棱台的下底面面积为,
所以该花灯的表面积为.
故选:A.
5.D
利用已知条件算出上下底面的面积和棱台的高,再由体积公式计算.
由正三棱台的结构特征知,其上、下底面分别是边长为4和6的等边三角形,如图所示,
为两底面的中心,则为的中点,过作下底面垂线,垂足为,
,,,
棱台的高,
该正三棱台的上底面的面积为,下底面的面积为,
所以正三棱台的体积.
故选:D
6.C
由题意首先求出正四棱锥的高,再求出底面对角线长度的一半,最后由勾股定理即可得解.
设四棱锥的高为,根据已知条件可得,所以,
而,所以这个四棱锥的侧棱长为.
故选:C.
7.B
将多面体补形为三棱柱,过点F作平面平面与直线AB,DC分别交于点P,Q,且满足,利用,进行计算即可.
如图,可将多面体补形为三棱柱,
过点F作平面平面与直线AB,DC分别交于点P,Q,
且满足,由题知,
易知平面FPQ,∴,
连接EB,EC,则,∴.
故选:
8.A
如图所示:
过点作与点,不妨设上下底面圆圆心分别为,半径分别为,圆台的高,
由题意母线长为,其母线与底面所成的角为,即,
从而,,
又圆台的上、下底面半径之比为,即,
所以,圆台上下两个底面的面积分别为,
由圆台体积公式可知.
故选:A.
9.2
根据三棱柱侧面积公式即可求解.
因为正三棱柱的所有棱长均为,所以三棱柱的侧面是边长为的正方形,
所以侧面积,所以.
故答案为:2
10.
首先根据正棱台的侧面积得到斜高为1,再计算正棱台的高即可.
如图所示:
设正四棱台的侧高为,高为,
棱台的侧面积,所以.
所以.
故答案为:
11.
在原正方体纸盒上,分别将四点两两相连,如图所示,
因为为正方体的面对角线,
所以,
所以为正四面体,
所以表面积为:,
故答案为:.
12.21
如图正四棱锥,其中底面于,
侧棱,高,所以,
所以下底面边长,
因为平面平行于底面,且,,
所以在与相似,且,
所以,
则正方形面积,正方形面积,
所得的棱台体积为.
故答案为:21
13./0.125
根据锥体体积公式即可求解.
由于平面,
所以,
故答案为:
14.1167
根据题意画出正四棱台的直观图,其中底面是边长为20cm的正方形,底面是边长为10cm的正方形,侧面等腰梯形的高cm,记底面ABCD和底面的中心分别为与,则是正四棱台的高,
过作平面的垂线,垂足为,则,且,,
则,,
则,
侧面是等腰梯形,
,则,
则棱台的高,
则由棱台的体积公式得mL,
故答案为:1167.
15.(1)侧棱长为3,斜高为
(2)
(1)设SO为正四棱锥S﹣ABCD的高,则SO=1,作OM⊥BC,则M为BC 中点,连接OM,OB,则SO⊥OB,SO⊥OM,由此能求出棱锥的侧棱长和斜高.
(2)棱锥的表面积,由此能求出结果.
(1)设SO为正四棱锥S﹣ABCD的高,则SO=1,
作OM⊥BC于M,则M为BC 中点,
连接OM,OB,则SO⊥OB,SO⊥OM,
BC=4,BM=2,则OM=2,OB=,
在Rt△SOB中,,
在Rt△SOM中,,
∴棱锥的侧棱长为3,斜高为.
(2)棱锥的表面积:
.
16.(1)10;
(2).
(1)利用长方体的表面积公式计算即得.
(2)利用锥体体积公式计算即得.
(1)长方体中,,,
因此长方体的侧面积,
所以长方体的表面积.
(2)的面积,
显然三棱锥的高为,
所以三棱锥的体积.
17.(1)36
(2)12
(1)画出图形,设对应的边长,再根据侧面积是底面积的2倍列出对应的方程求解棱长,再计算表面积即可;
(2)利用锥体体积公式求解.
(1)如图,设,是斜高,
,,.
在中,,,,
.,,.
(2)正四棱锥的体积.
18.侧面积约为,体积约为
根据棱锥的侧面积公式和体积公式结合已知条件求解即可
根据题意可抽象出图(2),其中AC为高,则,,底面周长.
.
.
因此,这座金字塔的侧面积约为,体积约为.
19.(1)256
(2)96
(1)求出长方体的体积和四棱锥体积,相加后得到答案;
(2)求出几何体下部分侧面积,得到答案.
(1)长方体的体积为,四棱锥的体积为,
故该几何体的体积为;
(2)长方体侧面面积为,
故要将几何体下部分表面刷上涂料(除底面),需要刷涂料的表面积为96.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
