8.3用正多边形铺设地面培优练习(含答案)
文档属性
| 名称 | 8.3用正多边形铺设地面培优练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 614.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 17:39:04 | ||
图片预览


文档简介
8.3用正多边形铺设地面培优练习华东师大版2024—2025学年七年级下册
一、选择题
1.用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌.若只选用一种大小相同的正多边形瓷砖进行平面镶嵌,则不能铺满地面的是( )
A.B. C.D.
2.现有正三角形、正方形、正六边形、正八边形地砖,若只能选择一种地砖铺设地面,则可供选择的地砖有( )
A.1种 B.2种 C.3种 D.4种
3.酷爱思考的可培同学在学面镶嵌的知识后,决定为家里新装修的房子选择一些不同样式的瓷砖来铺设地板,在以下正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
4.某校校园里的一条小路使用正六边形、正方形、正三角形三种地砖按如图方式铺设.若这条小路共用了50块正六边形地砖,则正方形地砖的数量为( )
A.300块 B.301块 C.250块 D.251块
5.下列多边形的组合中,能够铺满地面的是( )
A.正方形与正六边形 B.正四边形和正八边形
C.正五边形和正八边形 D.正三角形和正十边形
二、填空题
6.陶瓷市场现有边长相等的正三角形,正方形,正五边形,正六边形的地板砖出售,某客想买其中的一种镶嵌着铺地板,则他不可以选择的是 .
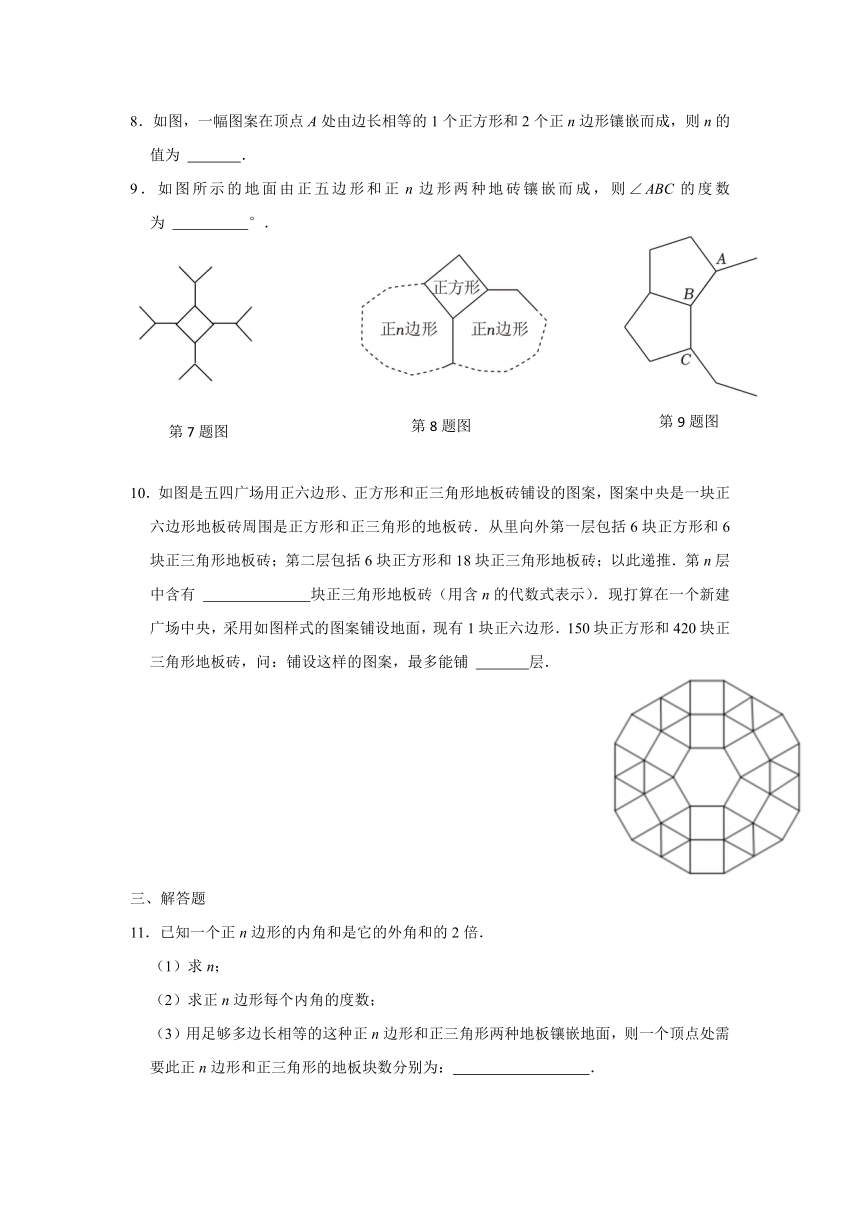
7.如图,是某校七年级数学兴趣小组活动室墙壁上的一幅图案;它是由边长相等的正方形和正n边形设计出来的,则n= .
8.如图,一幅图案在顶点A处由边长相等的1个正方形和2个正n边形镶嵌而成,则n的值为 .
9.如图所示的地面由正五边形和正n边形两种地砖镶嵌而成,则∠ABC的度数为 °.
10.如图是五四广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.第n层中含有 块正三角形地板砖(用含n的代数式表示).现打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形.150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺 层.
三、解答题
11.已知一个正n边形的内角和是它的外角和的2倍.
(1)求n;
(2)求正n边形每个内角的度数;
(3)用足够多边长相等的这种正n边形和正三角形两种地板镶嵌地面,则一个顶点处需要此正n边形和正三角形的地板块数分别为: .
12.由镶嵌知识可知,边长相等的正六边形、正方形、正三角形三种地砖可进行无缝密铺,观察图1、图2、图3,完成如下解答.
(1)填写下表:
图序 正六边形个数 正方形个数 正三角形个数
图1 1 6 6
图2 2
图3 3
(2)①图n中,正方形地砖数量为 块、正三角形地砖的数量为 块;
②求图10中正方形地砖和正三角形地砖的总数量.
13.在“平面图形的镶嵌”学习中,主要研究了一种或两种正多边形的镶嵌问题,请运用所学知识完成下列问题.
(1)填写表中空格.
正多边形的边数 3 4 5 6 8
正多边形每个内角的度数 60° 90°
(2)根据题意,如果仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)假设在镶嵌的平面图形的一个顶点周围有m个正四边形,n个正八边形,求m和n的值,请写出过程.
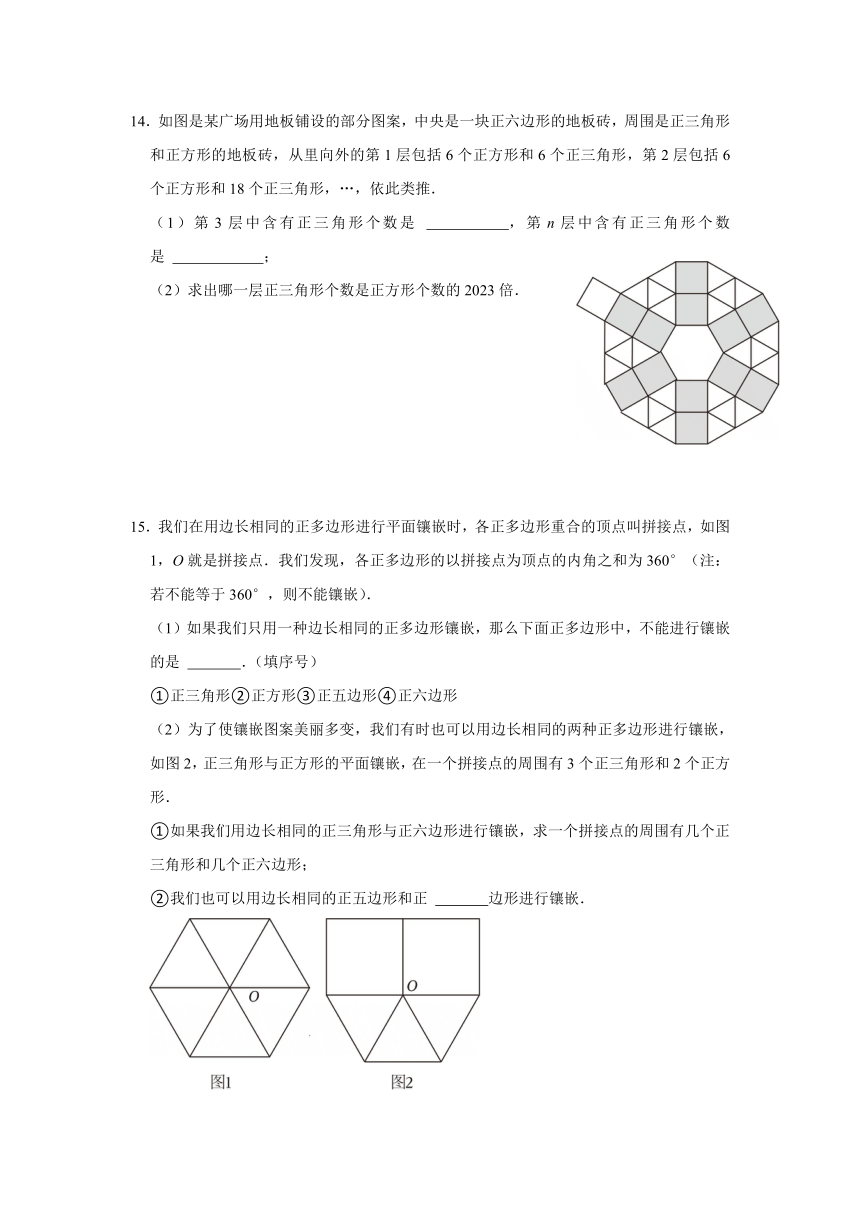
14.如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖,从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,…,依此类推.
(1)第3层中含有正三角形个数是 ,第n层中含有正三角形个数是 ;
(2)求出哪一层正三角形个数是正方形个数的2023倍.
15.我们在用边长相同的正多边形进行平面镶嵌时,各正多边形重合的顶点叫拼接点,如图1,O就是拼接点.我们发现,各正多边形的以拼接点为顶点的内角之和为360°(注:若不能等于360°,则不能镶嵌).
(1)如果我们只用一种边长相同的正多边形镶嵌,那么下面正多边形中,不能进行镶嵌的是 .(填序号)
①正三角形②正方形③正五边形④正六边形
(2)为了使镶嵌图案美丽多变,我们有时也可以用边长相同的两种正多边形进行镶嵌,如图2,正三角形与正方形的平面镶嵌,在一个拼接点的周围有3个正三角形和2个正方形.
①如果我们用边长相同的正三角形与正六边形进行镶嵌,求一个拼接点的周围有几个正三角形和几个正六边形;
②我们也可以用边长相同的正五边形和正 边形进行镶嵌.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C C B D B
二、填空题
6.【解答】解:结合镶嵌的条件是正多边形的一个内角的度数能整除360度进行求解可得:
正三角形的一个内角度数为60度,能整除360度,可以进行平面镶嵌;
正方形的一个内角度数为90度,能整除360度,可以进行平面镶嵌;
正五边形形的一个内角度数为,不能整除360度,不可以进行平面镶嵌;
正六边形形的一个内角度数为,能整除360度,可以进行平面镶嵌;
故答案为:正五边形.
7.【解答】解:正n边形的一个内角=(360°﹣90°)÷2=135°,
则135°n=(n﹣2) 180°,
解得n=8.
故答案为:8.
8.【解答】解:正方形的每个内角为90°,正n边形的每个内角为,根据题意得:
90°+2360°,
解得:n=8.
故答案为:8.
9.【解答】解:正五边形内角和 (5﹣2)×180°=540°,
所以每个内角度数540°÷8=108°,
∴∠ABC=360°﹣2×108°=144°.
故答案为:144.
10.【解答】解:∵第一层6=6×1=6×(2×1﹣1)块正三角形地板砖,
第二层18=6×3=6×(2×2﹣1)块正三角形地板砖,
第三层30=6×5=6×(2×3﹣1)块正三角形地板砖,
∴第n层6=6×1=6(2n﹣1)块正三角形地板砖;
∵150÷6=25(层),
∴150块正方形地板砖可以铺设这样的图案25层,
∵铺设n层需要正三角形地板砖的数量为:6[1+3+5+…+(2n﹣1)]=6n2,
∴6n2=420,
n2=70,
∴n,
又∵89,即8<n<9,
∴420块正三角形地板砖最多可以铺设这样的图案8层,
∴铺设这样的图案,最多能铺8层.
故答案为:6(2n﹣1),8.
三、解答题
11.【解答】解:(1)根据题意得:180°(n﹣2)=2×360°,
解得n=6.
答:n的值为6.
(2).
答:正n边形每个内角的度数为120°.
(3)设在平面镶嵌时,围绕在某一点有x个正六边形和y个正三角形的内角可以拼成一个周角,
根据题意可得:120x+60y=360,即:2x+y=6,
∴或,
∴一个顶点处需要此正六边形和正三角形的地板块数分别为:2个,2个或1个,4个.
故答案为:2个,2个或1个,4个.
12.【解答】解:(1)由所给图形可知:
图序 正六边形个数 正方形个数 正三角形个数
图1 1 6 6
图2 2 11 10
图3 3 16 14
(2)①观察图形可以得出正方形地砖会增加5块,三角形地砖会增加4块,
所以图n中,正方形地砖数量为(5n+1)块、正三角形地砖的数量为(4n+2)块;
故答案为:(5n+1),(4n+2);
②当n=10时,(5×10+1)+(4×10+2)=51+42=93(个),
答:图10中正方形地砖和正三角形地砖的总数量为93个.
13.【解答】解:(1)∵正n边形的内角为,
∴正五边形的内角为,正六边形的内角为:,正八边形的内角为,
故答案为:108°、120°、135°;
(2)∵仅用一种正多边形镶嵌,
∴360°÷60°=6,360°÷90°=4,,360°÷120°=3,,
∴仅用一种正多边形镶嵌,正三角形,正四边形,正六边形能镶嵌成平面图形;
(3)∵有m个正四边形,n个正八边形,
∴90°m+135°n=360°且m、n为正整数,
∴2m+3n=8,
∴当m=1时,n=2,满足题意;
当m=2时,,不满足题意;
当m=3时,,不满足题意;
当m=4时,n=0,不满足题意;
∴m=1,n=2,
即m的值为1,n的值为2.
14.【解答】解:(1)根据图形变化总结如下:
第1层每两个正方形之间有1个正三角形,该层共有6个正三角形,
第2层每两个正方形之间有3个正三角形,该层共有18个正三角形,
第3层每两个正方形之间有5个正三角形,该层共有30个正三角形,
…
∴第n层每两个正方形之间有(2n﹣1)个正三角形,该层共有6×(2n﹣1)=12n﹣6个正三角形.
故第3层中含有正三角形个数是30,第n层中含有正三角形个数是12n﹣6.
(2)设第n层正三角形个数是正方形个数的2023倍
根据图形,每一层都有6个正方长,则第n层的正方形还是6.
由(1)知第n层中含有正三角形个数是12n﹣6,
根据题意得:6×2023=12n﹣6,
解得:n=1012.
故第1012层正三角形个数是正方形个数的2023倍.
15.【解答】解:(1)①正三角形的内角为60°,360°÷60°=6,结果是整数,可以进行平面镶嵌;
②正方形内角为90°,360°÷90°=4,结果是整数,可以进行平面镶嵌;
③正五边形内角为108°,,结果不是整数,不可以进行平面镶嵌;
④正六边形内角为120°,360°÷120°=3,结果是整数,可以进行平面镶嵌;
故选:③;
(2)①设在平面镶嵌时,一个拼接点的周围有x个正三角形和y个正六边形,
根据题意得:60°x+120°y=360°,
∴x+2y=6,
∵x,y为正整数,
∴或,
答:在平面镶嵌时,一个拼接点的周围有2个正三角形和2个正六边形或4个正三角形和1个正六边形;
②由于正五边形内角为108°,设用边长相同的a个正五边形和b个正n边形进行镶嵌,
则,
整理得:,
∵a,b,n为正整数,
∴应为正整数,
则n=5或n=10,
当n=5时,3a+3b=10,此时a,b无正整数解,
当n=10时,3a+4b=10,解得正整数解为:,
故答案为:十.
一、选择题
1.用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌.若只选用一种大小相同的正多边形瓷砖进行平面镶嵌,则不能铺满地面的是( )
A.B. C.D.
2.现有正三角形、正方形、正六边形、正八边形地砖,若只能选择一种地砖铺设地面,则可供选择的地砖有( )
A.1种 B.2种 C.3种 D.4种
3.酷爱思考的可培同学在学面镶嵌的知识后,决定为家里新装修的房子选择一些不同样式的瓷砖来铺设地板,在以下正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
4.某校校园里的一条小路使用正六边形、正方形、正三角形三种地砖按如图方式铺设.若这条小路共用了50块正六边形地砖,则正方形地砖的数量为( )
A.300块 B.301块 C.250块 D.251块
5.下列多边形的组合中,能够铺满地面的是( )
A.正方形与正六边形 B.正四边形和正八边形
C.正五边形和正八边形 D.正三角形和正十边形
二、填空题
6.陶瓷市场现有边长相等的正三角形,正方形,正五边形,正六边形的地板砖出售,某客想买其中的一种镶嵌着铺地板,则他不可以选择的是 .
7.如图,是某校七年级数学兴趣小组活动室墙壁上的一幅图案;它是由边长相等的正方形和正n边形设计出来的,则n= .
8.如图,一幅图案在顶点A处由边长相等的1个正方形和2个正n边形镶嵌而成,则n的值为 .
9.如图所示的地面由正五边形和正n边形两种地砖镶嵌而成,则∠ABC的度数为 °.
10.如图是五四广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.第n层中含有 块正三角形地板砖(用含n的代数式表示).现打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形.150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺 层.
三、解答题
11.已知一个正n边形的内角和是它的外角和的2倍.
(1)求n;
(2)求正n边形每个内角的度数;
(3)用足够多边长相等的这种正n边形和正三角形两种地板镶嵌地面,则一个顶点处需要此正n边形和正三角形的地板块数分别为: .
12.由镶嵌知识可知,边长相等的正六边形、正方形、正三角形三种地砖可进行无缝密铺,观察图1、图2、图3,完成如下解答.
(1)填写下表:
图序 正六边形个数 正方形个数 正三角形个数
图1 1 6 6
图2 2
图3 3
(2)①图n中,正方形地砖数量为 块、正三角形地砖的数量为 块;
②求图10中正方形地砖和正三角形地砖的总数量.
13.在“平面图形的镶嵌”学习中,主要研究了一种或两种正多边形的镶嵌问题,请运用所学知识完成下列问题.
(1)填写表中空格.
正多边形的边数 3 4 5 6 8
正多边形每个内角的度数 60° 90°
(2)根据题意,如果仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)假设在镶嵌的平面图形的一个顶点周围有m个正四边形,n个正八边形,求m和n的值,请写出过程.
14.如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖,从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,…,依此类推.
(1)第3层中含有正三角形个数是 ,第n层中含有正三角形个数是 ;
(2)求出哪一层正三角形个数是正方形个数的2023倍.
15.我们在用边长相同的正多边形进行平面镶嵌时,各正多边形重合的顶点叫拼接点,如图1,O就是拼接点.我们发现,各正多边形的以拼接点为顶点的内角之和为360°(注:若不能等于360°,则不能镶嵌).
(1)如果我们只用一种边长相同的正多边形镶嵌,那么下面正多边形中,不能进行镶嵌的是 .(填序号)
①正三角形②正方形③正五边形④正六边形
(2)为了使镶嵌图案美丽多变,我们有时也可以用边长相同的两种正多边形进行镶嵌,如图2,正三角形与正方形的平面镶嵌,在一个拼接点的周围有3个正三角形和2个正方形.
①如果我们用边长相同的正三角形与正六边形进行镶嵌,求一个拼接点的周围有几个正三角形和几个正六边形;
②我们也可以用边长相同的正五边形和正 边形进行镶嵌.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C C B D B
二、填空题
6.【解答】解:结合镶嵌的条件是正多边形的一个内角的度数能整除360度进行求解可得:
正三角形的一个内角度数为60度,能整除360度,可以进行平面镶嵌;
正方形的一个内角度数为90度,能整除360度,可以进行平面镶嵌;
正五边形形的一个内角度数为,不能整除360度,不可以进行平面镶嵌;
正六边形形的一个内角度数为,能整除360度,可以进行平面镶嵌;
故答案为:正五边形.
7.【解答】解:正n边形的一个内角=(360°﹣90°)÷2=135°,
则135°n=(n﹣2) 180°,
解得n=8.
故答案为:8.
8.【解答】解:正方形的每个内角为90°,正n边形的每个内角为,根据题意得:
90°+2360°,
解得:n=8.
故答案为:8.
9.【解答】解:正五边形内角和 (5﹣2)×180°=540°,
所以每个内角度数540°÷8=108°,
∴∠ABC=360°﹣2×108°=144°.
故答案为:144.
10.【解答】解:∵第一层6=6×1=6×(2×1﹣1)块正三角形地板砖,
第二层18=6×3=6×(2×2﹣1)块正三角形地板砖,
第三层30=6×5=6×(2×3﹣1)块正三角形地板砖,
∴第n层6=6×1=6(2n﹣1)块正三角形地板砖;
∵150÷6=25(层),
∴150块正方形地板砖可以铺设这样的图案25层,
∵铺设n层需要正三角形地板砖的数量为:6[1+3+5+…+(2n﹣1)]=6n2,
∴6n2=420,
n2=70,
∴n,
又∵89,即8<n<9,
∴420块正三角形地板砖最多可以铺设这样的图案8层,
∴铺设这样的图案,最多能铺8层.
故答案为:6(2n﹣1),8.
三、解答题
11.【解答】解:(1)根据题意得:180°(n﹣2)=2×360°,
解得n=6.
答:n的值为6.
(2).
答:正n边形每个内角的度数为120°.
(3)设在平面镶嵌时,围绕在某一点有x个正六边形和y个正三角形的内角可以拼成一个周角,
根据题意可得:120x+60y=360,即:2x+y=6,
∴或,
∴一个顶点处需要此正六边形和正三角形的地板块数分别为:2个,2个或1个,4个.
故答案为:2个,2个或1个,4个.
12.【解答】解:(1)由所给图形可知:
图序 正六边形个数 正方形个数 正三角形个数
图1 1 6 6
图2 2 11 10
图3 3 16 14
(2)①观察图形可以得出正方形地砖会增加5块,三角形地砖会增加4块,
所以图n中,正方形地砖数量为(5n+1)块、正三角形地砖的数量为(4n+2)块;
故答案为:(5n+1),(4n+2);
②当n=10时,(5×10+1)+(4×10+2)=51+42=93(个),
答:图10中正方形地砖和正三角形地砖的总数量为93个.
13.【解答】解:(1)∵正n边形的内角为,
∴正五边形的内角为,正六边形的内角为:,正八边形的内角为,
故答案为:108°、120°、135°;
(2)∵仅用一种正多边形镶嵌,
∴360°÷60°=6,360°÷90°=4,,360°÷120°=3,,
∴仅用一种正多边形镶嵌,正三角形,正四边形,正六边形能镶嵌成平面图形;
(3)∵有m个正四边形,n个正八边形,
∴90°m+135°n=360°且m、n为正整数,
∴2m+3n=8,
∴当m=1时,n=2,满足题意;
当m=2时,,不满足题意;
当m=3时,,不满足题意;
当m=4时,n=0,不满足题意;
∴m=1,n=2,
即m的值为1,n的值为2.
14.【解答】解:(1)根据图形变化总结如下:
第1层每两个正方形之间有1个正三角形,该层共有6个正三角形,
第2层每两个正方形之间有3个正三角形,该层共有18个正三角形,
第3层每两个正方形之间有5个正三角形,该层共有30个正三角形,
…
∴第n层每两个正方形之间有(2n﹣1)个正三角形,该层共有6×(2n﹣1)=12n﹣6个正三角形.
故第3层中含有正三角形个数是30,第n层中含有正三角形个数是12n﹣6.
(2)设第n层正三角形个数是正方形个数的2023倍
根据图形,每一层都有6个正方长,则第n层的正方形还是6.
由(1)知第n层中含有正三角形个数是12n﹣6,
根据题意得:6×2023=12n﹣6,
解得:n=1012.
故第1012层正三角形个数是正方形个数的2023倍.
15.【解答】解:(1)①正三角形的内角为60°,360°÷60°=6,结果是整数,可以进行平面镶嵌;
②正方形内角为90°,360°÷90°=4,结果是整数,可以进行平面镶嵌;
③正五边形内角为108°,,结果不是整数,不可以进行平面镶嵌;
④正六边形内角为120°,360°÷120°=3,结果是整数,可以进行平面镶嵌;
故选:③;
(2)①设在平面镶嵌时,一个拼接点的周围有x个正三角形和y个正六边形,
根据题意得:60°x+120°y=360°,
∴x+2y=6,
∵x,y为正整数,
∴或,
答:在平面镶嵌时,一个拼接点的周围有2个正三角形和2个正六边形或4个正三角形和1个正六边形;
②由于正五边形内角为108°,设用边长相同的a个正五边形和b个正n边形进行镶嵌,
则,
整理得:,
∵a,b,n为正整数,
∴应为正整数,
则n=5或n=10,
当n=5时,3a+3b=10,此时a,b无正整数解,
当n=10时,3a+4b=10,解得正整数解为:,
故答案为:十.
