苏教版六年级下册数学几何思维练习题课件(共22张PPT)
文档属性
| 名称 | 苏教版六年级下册数学几何思维练习题课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 14:33:25 | ||
图片预览



文档简介
(共22张PPT)
图形问题
思维提升课
六年级
目
录
知识要点
例题讲解
巩固练习
提升练习
1
2
3
4
知识要点
在计算平面图形问题时,有时会在已知条件与所求问题之间找不到任何联系,感到无从下手。
这时,我们首先要认真观察图形,分析、研究已知条件,挖掘隐含的已知条件。通过添加辅助线,平移旋转,剪拼组合等方法构成新的图形,再经过分析推导,寻出解题途径,求出答案。
经典例题 1
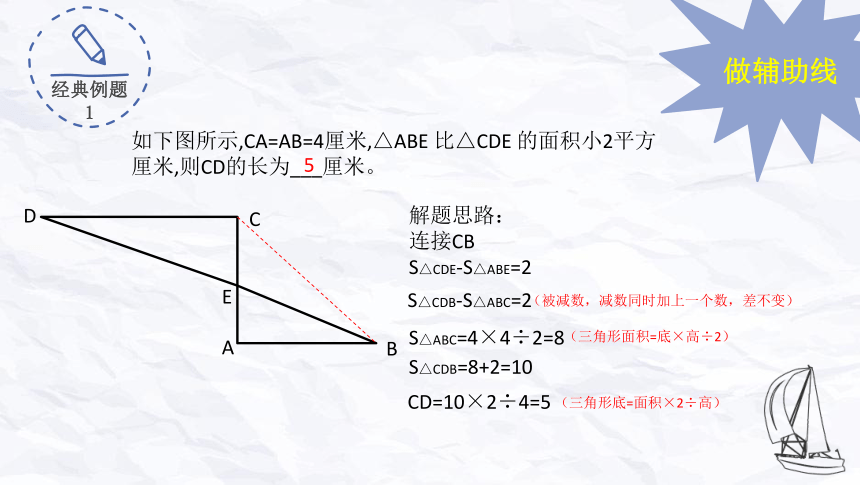
如下图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,则CD的长为___厘米。
D
C
A
B
E
做辅助线
解题思路:
连接CB
S△CDE-S△ABE=2
S△ABC=4×4÷2=8
S△CDB=8+2=10
CD=10×2÷4=5
S△CDB-S△ABC=2
(被减数,减数同时加上一个数,差不变)
(三角形面积=底×高÷2)
(三角形底=面积×2÷高)
5
经典例题 2
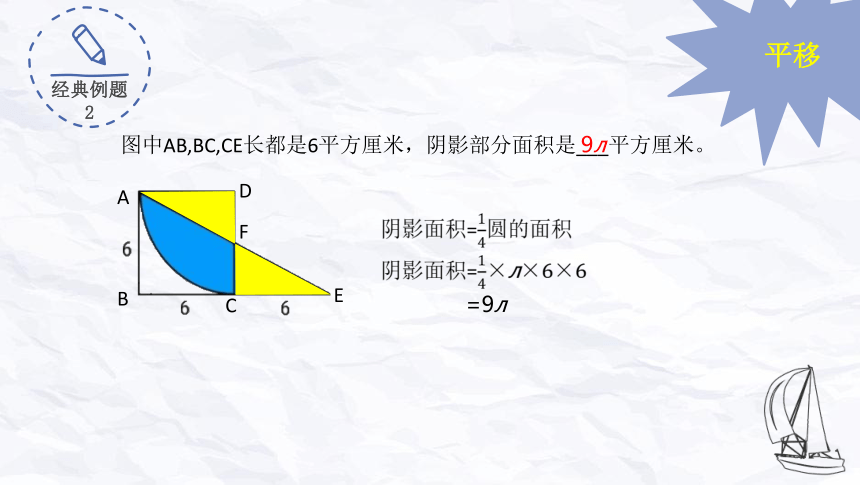
图中AB,BC,CE长都是6平方厘米,阴影部分面积是___平方厘米。
平移
阴影面积=圆的面积
阴影面积=×л×6×6
=9л
9л
A
C
B
D
E
F
经典例题 3
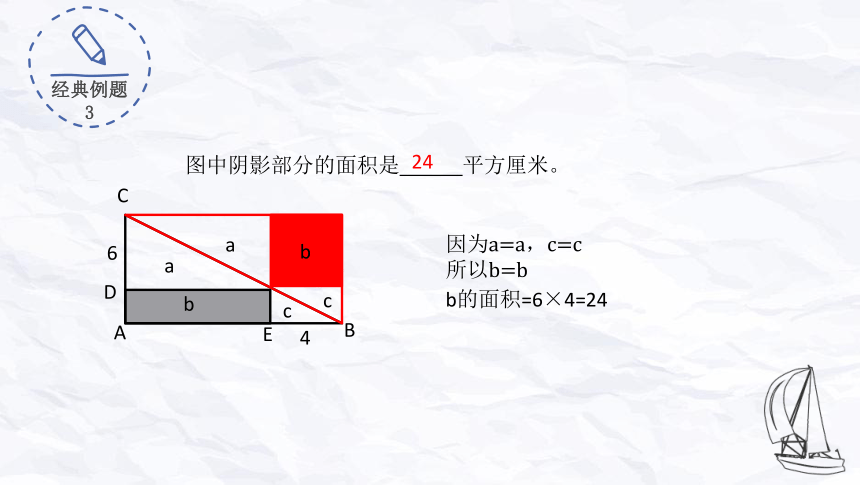
图中阴影部分的面积是 平方厘米。
因为a=a,c=c
所以b=b
A
E
D
A
C
B
4
6
a
a
b
b
c
c
b的面积=6×4=24
24
经典例题 4
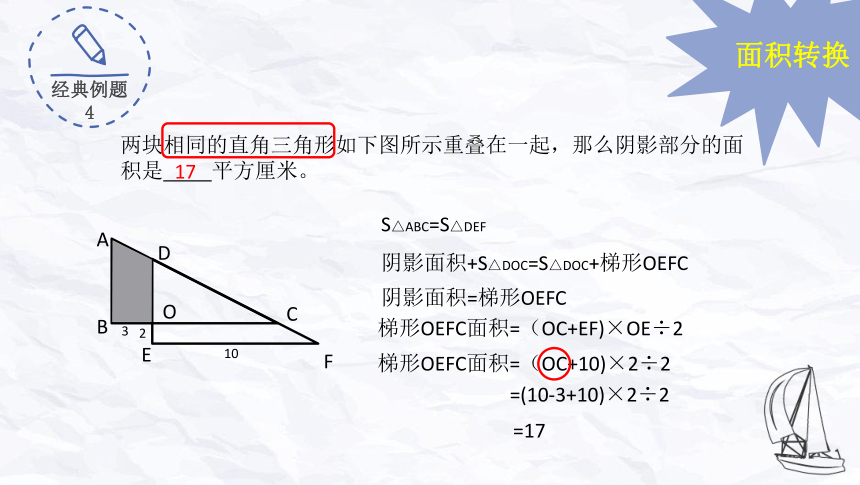
两块相同的直角三角形如下图所示重叠在一起,那么阴影部分的面积是 平方厘米。
S△ABC=S△DEF
A
B
O
E
F
D
3
C
10
2
阴影面积+S△DOC=S△DOC+梯形OEFC
阴影面积=梯形OEFC
梯形OEFC面积=(OC+EF)×OE÷2
梯形OEFC面积=(OC+10)×2÷2
=(10-3+10)×2÷2
=17
17
面积转换
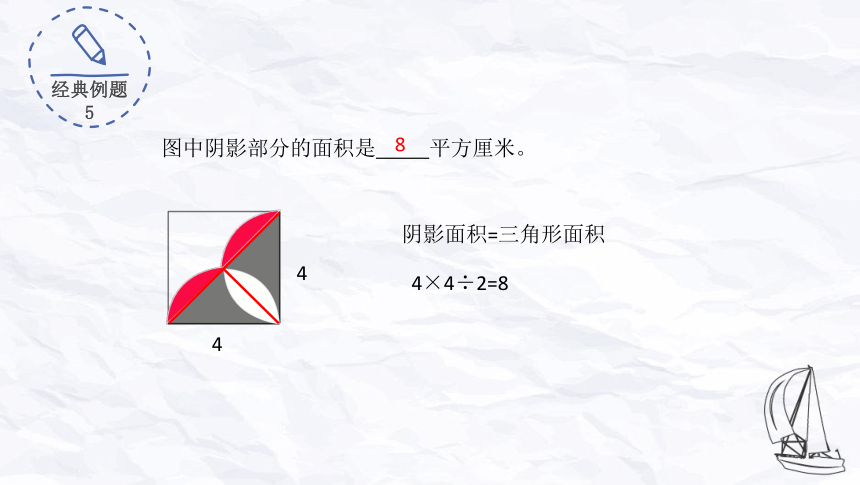
经典例题 5
图中阴影部分的面积是 平方厘米。
4
4
阴影面积=三角形面积
4×4÷2=8
8
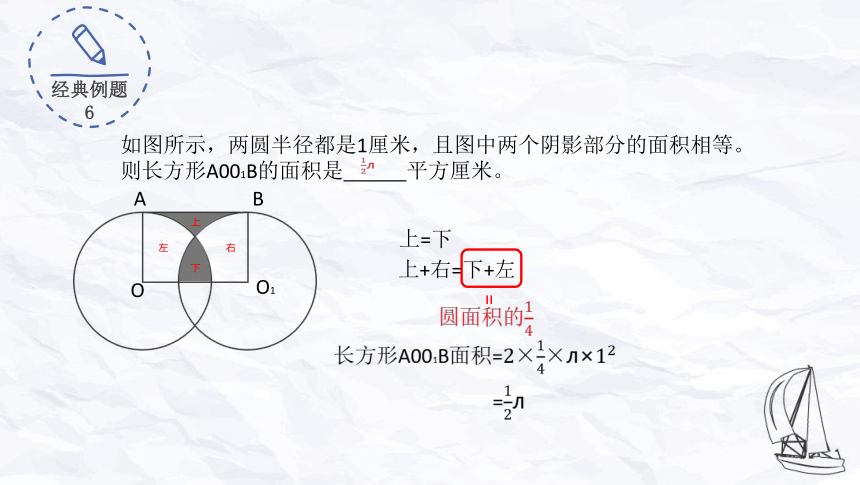
经典例题 6
如图所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等。则长方形A001B的面积是 平方厘米。
O1
O
B
A
左
上
下
右
上=下
上+右=下+左
=
圆面积的
长方形A001B面积=2××л×
=л
л
运用练习 1
图中阴影部分的面积是 平方厘米。
5cm
8cm
A
F
B
D
C
E
H
方法一:
△ACF面积=(5+8)×5÷2=32.5
△ACH面积=△ACD面积-△DCH面积
△ACH面积=(5+8)×8÷2-8×8÷2
=52-32
=20
阴影部分面积=32.5-20=12
方法二:
M
阴影部分面积=△AMD-△ANF-△EFD-四边形NFEM
N
等底等高
=(5+8)×8÷2-5×5÷2-(8-5)×8÷2-5×(8-5)
=52-12.5-12-15
=12.5
12.5
运用练习 2
如图所示,△ABC和△DEF是两个完全相同的等腰直角三角形直角边长等于9厘米,阴影部分的面积是 平方厘米。
切割平移
阴影面积=3×3×3
=27
E
B
3
O
M
N
F
C
D
A
6
3
3
3
3
3
27
运用练习 3
如图下图中,正方形ABCD的边长是5厘米,且三角形CEF的面积比三角形ADF的面积大5平方厘米,则CE的长是 厘米。
正方形ABCD=5×5=25=梯形ABCF+△AFD
△ABE=梯形ABCF+△FCE
A
C
B
D
E
F
大5
=梯形ABCF+△AFD+5
=25+5
=30
BE=30×2÷5=12
CE=12-5=7
7
运用练习 4
如下图所示,BE长5厘米,长方形AEFD的面积是35平方厘米。
则CD长 厘米。
35÷5=7
C
E
A
B
F
D
35
35
7
运用练习 5
图中阴影部分的面积是 平方厘米。
a的面积=正方形面积-圆的面积
阴影面积=△面积-a
=(6+4)×4÷2-(16-4π)
6
4
a
=4×4-××π
=16-4π
=4+4π
4+4π
运用练习 6
图中阴影部分的面积是 平方厘米。
阴影面积=大圆的面积-三角形面积
×π×-10×10÷2
16π-50
8
8
=16π-50
运用练习 7
图中阴影部分的面积是 平方厘米。(π=3.14)
阴影面积=正方形面积-四个空白部分面积
两个空白部分面积=正方形面积-一个圆的面积
10
10
=10×10-π×
=100-25×3.14
=21.5
阴影面积=10×10-21.5×2=57
57
4mm
2mm
6mm
运用练习 8
图中阴影部分的面积是 平方厘米。
6mm
4mm
方法一:
阴影部分面积=梯形面积-两个三角形面积
=(6+4+4)×6÷2-4×2÷2-4×(6+4)÷2
=42-4-20
=18
方法一:
添加辅助线
因为△BEC面积=△AEC面积(等底等高的三角形面积相等)
所以△BEH面积=△AHC面积
B
A
H
F
6mm
E
C
所以阴影部分面积=△ABE的面积
=6×6÷2
=18
18
运用练习 7
如下图所示,在边长为8厘米的正方形中画了两个四分之一圆。图中阴影①的面积比阴影②的面积大 平方厘米。
求①-②=?
转化为(①+左)-(②+右)=?(被减数,减数同时加一个数,差不变)
②
①
左
右
=
=
)
×π×-(8×8-×π×)
=32π-64
32π-64
提升练习 1
下图中,四边形ABCD为平行四边形,三角形MAB的面积是11平方厘米,三角形MDC的面积是5平方厘米。那么平行四边形ABCD的面积是 平方厘米。
A
B
C
D
M
做辅助线
E
F
S△ABM=11,则平行四边形ABFE面积=11×2=22
S△MDC=5,则平行四边形DCFE面积=5×2=10
平行四边形ABCD面积=平行四边形ABFE面积-平行四边形DCFE面积
平行四边形ABCD面积=22-10=12
补成大平行四边形,将已知条件和问题连接起来
12
提升练习 2
小华提议把一块大巧克力按照下图分成四块,每块大小如图。若长方形APHM、BNHP、CQHN的面积分别为12、6、10、则阴影部分的面积是___。
S△ADP=×(12+20)=16 S△DCN=×(20+10)=15 S△PBN=×6=3
四边形MDQH面积=MH×HQ
=(MH×PH×HQ×HN)÷(PH×HN)=?
求阴影面积,可以反向求空白部分三个三角形面积,△ABM=长方形PHNB面积,△ADP=长方形ADQP面积,△DCP面积=方形MDCN面积,这样就需要知道四边形ADQP,MDCN面积,就需要先求出四边形MDQH面积,可以根据题目条件求
14
P
H
Q
N
M
C
D
B
A
S△PDN=12+6+10+20-16-15-3=14
( 12 × 10 ) ÷ 6 =20
提升练习 3
0是长方形ABCD内的一点,已知△0BC的面积是5平方厘米,△AB0的面积是2平方厘米,那么△0BD的面积是 平方厘米
O
D
A
C
B
S△AOD+S△BCO=×AD×h1+×BC×h2
h1
h2
=×AD×h1+×AD×h2
=×AD×(h1+h2)
=×AD×AB=长方形ABCD面积
S△ABD=长方形ABCD面积
S△AOD+S△BCO=S△ABD=S△ABO+S△AOD+S△OBD
S△BCO=S△ABO+S△OBD
5 2
S△OBD=5-2=3
3
谢谢观看
图形问题
思维提升课
六年级
目
录
知识要点
例题讲解
巩固练习
提升练习
1
2
3
4
知识要点
在计算平面图形问题时,有时会在已知条件与所求问题之间找不到任何联系,感到无从下手。
这时,我们首先要认真观察图形,分析、研究已知条件,挖掘隐含的已知条件。通过添加辅助线,平移旋转,剪拼组合等方法构成新的图形,再经过分析推导,寻出解题途径,求出答案。
经典例题 1
如下图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,则CD的长为___厘米。
D
C
A
B
E
做辅助线
解题思路:
连接CB
S△CDE-S△ABE=2
S△ABC=4×4÷2=8
S△CDB=8+2=10
CD=10×2÷4=5
S△CDB-S△ABC=2
(被减数,减数同时加上一个数,差不变)
(三角形面积=底×高÷2)
(三角形底=面积×2÷高)
5
经典例题 2
图中AB,BC,CE长都是6平方厘米,阴影部分面积是___平方厘米。
平移
阴影面积=圆的面积
阴影面积=×л×6×6
=9л
9л
A
C
B
D
E
F
经典例题 3
图中阴影部分的面积是 平方厘米。
因为a=a,c=c
所以b=b
A
E
D
A
C
B
4
6
a
a
b
b
c
c
b的面积=6×4=24
24
经典例题 4
两块相同的直角三角形如下图所示重叠在一起,那么阴影部分的面积是 平方厘米。
S△ABC=S△DEF
A
B
O
E
F
D
3
C
10
2
阴影面积+S△DOC=S△DOC+梯形OEFC
阴影面积=梯形OEFC
梯形OEFC面积=(OC+EF)×OE÷2
梯形OEFC面积=(OC+10)×2÷2
=(10-3+10)×2÷2
=17
17
面积转换
经典例题 5
图中阴影部分的面积是 平方厘米。
4
4
阴影面积=三角形面积
4×4÷2=8
8
经典例题 6
如图所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等。则长方形A001B的面积是 平方厘米。
O1
O
B
A
左
上
下
右
上=下
上+右=下+左
=
圆面积的
长方形A001B面积=2××л×
=л
л
运用练习 1
图中阴影部分的面积是 平方厘米。
5cm
8cm
A
F
B
D
C
E
H
方法一:
△ACF面积=(5+8)×5÷2=32.5
△ACH面积=△ACD面积-△DCH面积
△ACH面积=(5+8)×8÷2-8×8÷2
=52-32
=20
阴影部分面积=32.5-20=12
方法二:
M
阴影部分面积=△AMD-△ANF-△EFD-四边形NFEM
N
等底等高
=(5+8)×8÷2-5×5÷2-(8-5)×8÷2-5×(8-5)
=52-12.5-12-15
=12.5
12.5
运用练习 2
如图所示,△ABC和△DEF是两个完全相同的等腰直角三角形直角边长等于9厘米,阴影部分的面积是 平方厘米。
切割平移
阴影面积=3×3×3
=27
E
B
3
O
M
N
F
C
D
A
6
3
3
3
3
3
27
运用练习 3
如图下图中,正方形ABCD的边长是5厘米,且三角形CEF的面积比三角形ADF的面积大5平方厘米,则CE的长是 厘米。
正方形ABCD=5×5=25=梯形ABCF+△AFD
△ABE=梯形ABCF+△FCE
A
C
B
D
E
F
大5
=梯形ABCF+△AFD+5
=25+5
=30
BE=30×2÷5=12
CE=12-5=7
7
运用练习 4
如下图所示,BE长5厘米,长方形AEFD的面积是35平方厘米。
则CD长 厘米。
35÷5=7
C
E
A
B
F
D
35
35
7
运用练习 5
图中阴影部分的面积是 平方厘米。
a的面积=正方形面积-圆的面积
阴影面积=△面积-a
=(6+4)×4÷2-(16-4π)
6
4
a
=4×4-××π
=16-4π
=4+4π
4+4π
运用练习 6
图中阴影部分的面积是 平方厘米。
阴影面积=大圆的面积-三角形面积
×π×-10×10÷2
16π-50
8
8
=16π-50
运用练习 7
图中阴影部分的面积是 平方厘米。(π=3.14)
阴影面积=正方形面积-四个空白部分面积
两个空白部分面积=正方形面积-一个圆的面积
10
10
=10×10-π×
=100-25×3.14
=21.5
阴影面积=10×10-21.5×2=57
57
4mm
2mm
6mm
运用练习 8
图中阴影部分的面积是 平方厘米。
6mm
4mm
方法一:
阴影部分面积=梯形面积-两个三角形面积
=(6+4+4)×6÷2-4×2÷2-4×(6+4)÷2
=42-4-20
=18
方法一:
添加辅助线
因为△BEC面积=△AEC面积(等底等高的三角形面积相等)
所以△BEH面积=△AHC面积
B
A
H
F
6mm
E
C
所以阴影部分面积=△ABE的面积
=6×6÷2
=18
18
运用练习 7
如下图所示,在边长为8厘米的正方形中画了两个四分之一圆。图中阴影①的面积比阴影②的面积大 平方厘米。
求①-②=?
转化为(①+左)-(②+右)=?(被减数,减数同时加一个数,差不变)
②
①
左
右
=
=
)
×π×-(8×8-×π×)
=32π-64
32π-64
提升练习 1
下图中,四边形ABCD为平行四边形,三角形MAB的面积是11平方厘米,三角形MDC的面积是5平方厘米。那么平行四边形ABCD的面积是 平方厘米。
A
B
C
D
M
做辅助线
E
F
S△ABM=11,则平行四边形ABFE面积=11×2=22
S△MDC=5,则平行四边形DCFE面积=5×2=10
平行四边形ABCD面积=平行四边形ABFE面积-平行四边形DCFE面积
平行四边形ABCD面积=22-10=12
补成大平行四边形,将已知条件和问题连接起来
12
提升练习 2
小华提议把一块大巧克力按照下图分成四块,每块大小如图。若长方形APHM、BNHP、CQHN的面积分别为12、6、10、则阴影部分的面积是___。
S△ADP=×(12+20)=16 S△DCN=×(20+10)=15 S△PBN=×6=3
四边形MDQH面积=MH×HQ
=(MH×PH×HQ×HN)÷(PH×HN)=?
求阴影面积,可以反向求空白部分三个三角形面积,△ABM=长方形PHNB面积,△ADP=长方形ADQP面积,△DCP面积=方形MDCN面积,这样就需要知道四边形ADQP,MDCN面积,就需要先求出四边形MDQH面积,可以根据题目条件求
14
P
H
Q
N
M
C
D
B
A
S△PDN=12+6+10+20-16-15-3=14
( 12 × 10 ) ÷ 6 =20
提升练习 3
0是长方形ABCD内的一点,已知△0BC的面积是5平方厘米,△AB0的面积是2平方厘米,那么△0BD的面积是 平方厘米
O
D
A
C
B
S△AOD+S△BCO=×AD×h1+×BC×h2
h1
h2
=×AD×h1+×AD×h2
=×AD×(h1+h2)
=×AD×AB=长方形ABCD面积
S△ABD=长方形ABCD面积
S△AOD+S△BCO=S△ABD=S△ABO+S△AOD+S△OBD
S△BCO=S△ABO+S△OBD
5 2
S△OBD=5-2=3
3
谢谢观看
同课章节目录
