9.1.2轴对称的再认识培优练习华东师大版2024—2025学年七年级下册
文档属性
| 名称 | 9.1.2轴对称的再认识培优练习华东师大版2024—2025学年七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 649.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 17:42:37 | ||
图片预览


文档简介
9.1.2轴对称的再认识培优练习华东师大版2024—2025学年七年级下册
一、选择题
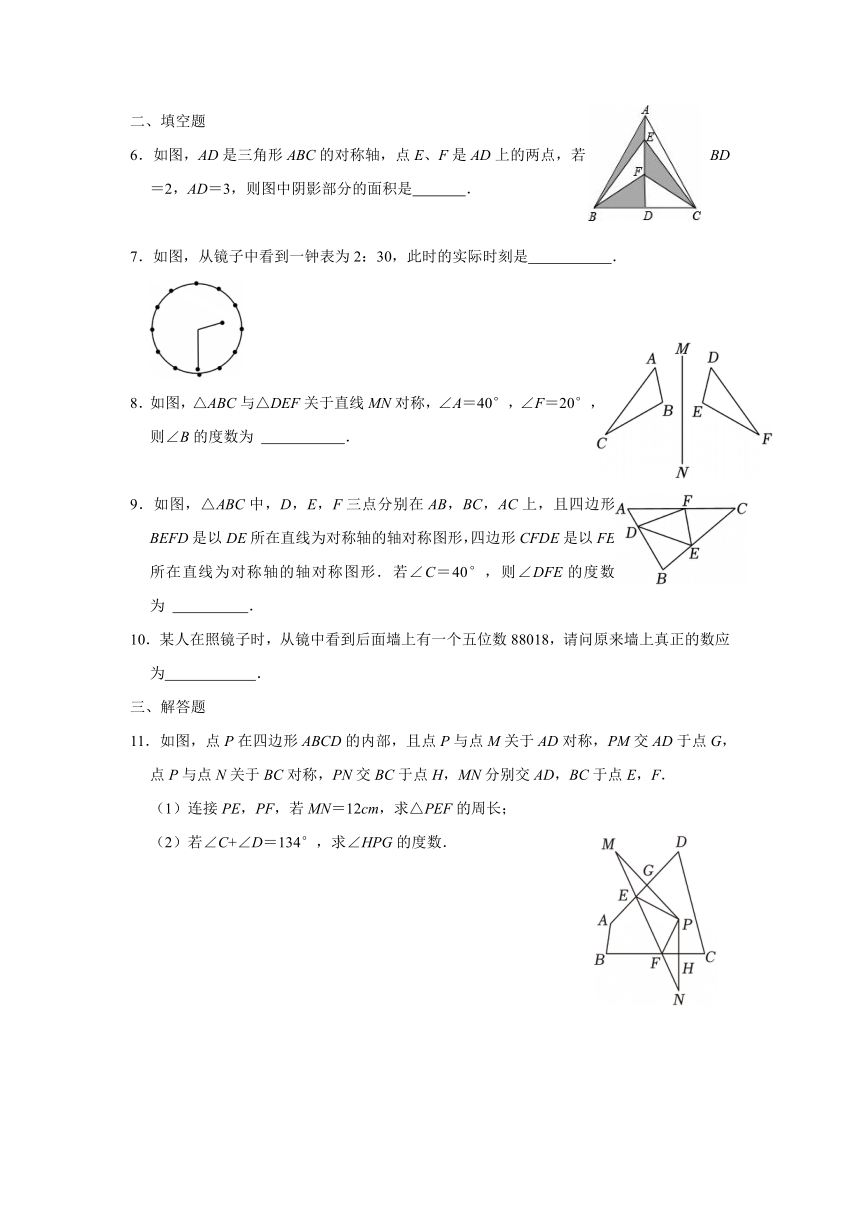
1.下列图形不是轴对称图形的是( )
A. B. C. D.
2.如图,∠AOB=40°,点M在∠AOB内,点M关于射线OA,OB的对称点分别是M1,M2,连接OM1,OM2,则∠M1OM2=( )
A.80° B.70°
C.60° D.无法确定
3.如图,下面是三位同学的折纸示意图,则AD依次是△ABC的( )
A.中线、角平分线、高线 B.高线、中线、角平分线
C.角平分线、高线、中线 D.角平分线、中线、高线
4.如图,△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定正确的是( )
A.∠ACB=∠A′C′B′ B.BO=B′O
C.AC⊥B′C′ D.AA′∥BB′
5.时钟在水中的倒影如图所示,此时时钟显示的时间是( )
A.12:20 B.02:21 C.15:50 D.05:51
二、填空题
6.如图,AD是三角形ABC的对称轴,点E、F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是 .
7.如图,从镜子中看到一钟表为2:30,此时的实际时刻是 .
8.如图,△ABC与△DEF关于直线MN对称,∠A=40°,∠F=20°,则∠B的度数为 .
9.如图,△ABC中,D,E,F三点分别在AB,BC,AC上,且四边形BEFD是以DE所在直线为对称轴的轴对称图形,四边形CFDE是以FE所在直线为对称轴的轴对称图形.若∠C=40°,则∠DFE的度数为 .
10.某人在照镜子时,从镜中看到后面墙上有一个五位数88018,请问原来墙上真正的数应为 .
三、解答题
11.如图,点P在四边形ABCD的内部,且点P与点M关于AD对称,PM交AD于点G,点P与点N关于BC对称,PN交BC于点H,MN分别交AD,BC于点E,F.
(1)连接PE,PF,若MN=12cm,求△PEF的周长;
(2)若∠C+∠D=134°,求∠HPG的度数.
12.如图,已知点P在∠AOB的内部,且点P与点M关于OA对称,PM交OA于点Q,点P与点N关于OB对称,PN交OB于点R,MN分别交OA,OB于点E,F.
(1)连接PE,PF,若MN=15,求△PEF的周长;
(2)若PM=PN,求证:OP平分∠AOB.
13.如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数;
(3)猜想:∠1+∠2与∠A的关系,请直接写出其关系式.
14.如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm.
(1)求△OEF的周长;
(2)若∠APB=α,求∠MPN(用含a的代数式表示).
15.如图,在△ABC中,AD平分∠BAC,点E为AC中点,AD与BE相交于点F.
(1)若∠ABC=38°,∠ACB=82°,求∠ADB的度数;
(2)过点B作BH⊥AD交AD延长线于点H,作△ABH关于AH对称的△AGH,设△BFH,△AEF的面积分别为S1,S2,若S△BCG=6,试求S1﹣S2的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C A C C A
二、填空题
6.【解答】解:∵AD是三角形ABC的对称轴,
∴AD垂直平分BC,
即AD⊥BC,BD=DC,
∴S△EFB=S△EFC,
∴S阴影部分=S△ABDS△ABCBD AD2×3=3.
故答案为3.
7.【解答】解:从镜子中看到一钟表的时针和分针,此时的实际时刻是9:30,
故答案为:9:30.
8.【解答】解:∵△ABC与△DEF关于直线l对称,∠A=40°,∠F=20°,
∴△ABC≌△DEF,
∴∠C=∠F=20°,
∴∠B=180°﹣∠A﹣∠C=180°﹣40°﹣20°=120°.
故答案为:120°.
9.【解答】解:∵四边形BEFD是以DE所在直线为对称轴的轴对称图形,四边形CFDE是以FE所在直线为对称轴的轴对称图形,
∴∠EDF=∠C=40°,∠BED=∠DEF=∠CEF,
∵∠BED+∠DEF+∠CEF=180°,
∴∠DEF=60°,
∴∠DFE=180°﹣∠EDF﹣∠DEF=180°﹣40°﹣60°=80°,
故答案为:80°.
10.【解答】解:根据镜面对称性质得出:实际五位数为81088,
故答案为81088.
三、解答题
11.【解答】解:(1)∵点P与点M关于AD对称,点P与点N关于BC对称,
∴EM=EP,FP=FN,
∴C△PEF=PE+PF+EF=ME+EF+FN=MN=12(cm).
(2)∵∠C+∠D=134°,
∴∠A+∠B=360°﹣134°=226°.
又∵PG⊥AD,PH⊥BC,
∴∠PGA=∠PHB=90°,
∴∠HPG=540°﹣90°﹣90°﹣226°=134°.
12.【解答】(1)解:∵点P与点M关于OA对称,
∴ME=PE.
同理:FN=PF.
∴△PEF的周长=EP+FP+EF=ME+EF+FN=MN=15;
(2)证明:∵PN=PM,Q、R为MP,PN的中点,
∴,,
∴PQ=PR.
又∵点P与点M关于OA对称,点P与点N关于OB对称,
∴PQ⊥QA,PR⊥OB,
∴OP平分∠AOB.
13.【解答】解:(1)∵在△ABC中,∠B=50°,∠C=60°,
∴∠A=180°﹣∠B﹣∠C=70°;
(2)∵将△ABC沿着DE折叠压平,A与A′重合,
∴,,
∴∠1+∠2=180°﹣∠AEA′+180°﹣∠ADA′=360°﹣2∠AED﹣2∠ADE,
∵∠AED+∠ADE+∠A=180°,
∴∠AED+∠ADE=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A,
∵∠1+∠2=130°,
∴;
(3)∵将△ABC沿着DE折叠压平,A与A′重合,
∴,,
∴∠1+∠2=180°﹣∠AEA′+180°﹣∠ADA′=360°﹣2∠AED﹣2∠ADE,
∵∠AED+∠ADE+∠A=180°,
∴∠AED+∠ADE=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.
14.【解答】解:(1)∵M,N分别是点O关于PA、PB的对称点,
∴EM=EO,FN=FO,
∴△OEF的周长=OE+OF+EF
=ME+EF+FN=MN
=5(cm);
(2)如图,连接PM,PN,PO,
∵M,N分别是点O关于PA、PB的对称点,
∴∠MPA=∠OPA,∠NPB=∠OPB,
∴∠MPN=2∠APB=2α.
15.【解答】解:(1)∵∠ABC=38°,∠ACD=82°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=30°,
∴∠ADB=∠DAC+∠ACD=30°+82°=112°;
(2)∵△ABH与△AGH关于AH对称
∴△ABH≌△AGH,
∴AB=AG,BH=HG,
∵S△BFH﹣S△AEF=S△ABH﹣S△ABES△ABGS△ABC,
∴S1﹣S2(S△ABG﹣S△ABC)S△BCG,
∵S△BCG=6,
∴S1﹣S2=3.
一、选择题
1.下列图形不是轴对称图形的是( )
A. B. C. D.
2.如图,∠AOB=40°,点M在∠AOB内,点M关于射线OA,OB的对称点分别是M1,M2,连接OM1,OM2,则∠M1OM2=( )
A.80° B.70°
C.60° D.无法确定
3.如图,下面是三位同学的折纸示意图,则AD依次是△ABC的( )
A.中线、角平分线、高线 B.高线、中线、角平分线
C.角平分线、高线、中线 D.角平分线、中线、高线
4.如图,△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定正确的是( )
A.∠ACB=∠A′C′B′ B.BO=B′O
C.AC⊥B′C′ D.AA′∥BB′
5.时钟在水中的倒影如图所示,此时时钟显示的时间是( )
A.12:20 B.02:21 C.15:50 D.05:51
二、填空题
6.如图,AD是三角形ABC的对称轴,点E、F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是 .
7.如图,从镜子中看到一钟表为2:30,此时的实际时刻是 .
8.如图,△ABC与△DEF关于直线MN对称,∠A=40°,∠F=20°,则∠B的度数为 .
9.如图,△ABC中,D,E,F三点分别在AB,BC,AC上,且四边形BEFD是以DE所在直线为对称轴的轴对称图形,四边形CFDE是以FE所在直线为对称轴的轴对称图形.若∠C=40°,则∠DFE的度数为 .
10.某人在照镜子时,从镜中看到后面墙上有一个五位数88018,请问原来墙上真正的数应为 .
三、解答题
11.如图,点P在四边形ABCD的内部,且点P与点M关于AD对称,PM交AD于点G,点P与点N关于BC对称,PN交BC于点H,MN分别交AD,BC于点E,F.
(1)连接PE,PF,若MN=12cm,求△PEF的周长;
(2)若∠C+∠D=134°,求∠HPG的度数.
12.如图,已知点P在∠AOB的内部,且点P与点M关于OA对称,PM交OA于点Q,点P与点N关于OB对称,PN交OB于点R,MN分别交OA,OB于点E,F.
(1)连接PE,PF,若MN=15,求△PEF的周长;
(2)若PM=PN,求证:OP平分∠AOB.
13.如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数;
(3)猜想:∠1+∠2与∠A的关系,请直接写出其关系式.
14.如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm.
(1)求△OEF的周长;
(2)若∠APB=α,求∠MPN(用含a的代数式表示).
15.如图,在△ABC中,AD平分∠BAC,点E为AC中点,AD与BE相交于点F.
(1)若∠ABC=38°,∠ACB=82°,求∠ADB的度数;
(2)过点B作BH⊥AD交AD延长线于点H,作△ABH关于AH对称的△AGH,设△BFH,△AEF的面积分别为S1,S2,若S△BCG=6,试求S1﹣S2的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C A C C A
二、填空题
6.【解答】解:∵AD是三角形ABC的对称轴,
∴AD垂直平分BC,
即AD⊥BC,BD=DC,
∴S△EFB=S△EFC,
∴S阴影部分=S△ABDS△ABCBD AD2×3=3.
故答案为3.
7.【解答】解:从镜子中看到一钟表的时针和分针,此时的实际时刻是9:30,
故答案为:9:30.
8.【解答】解:∵△ABC与△DEF关于直线l对称,∠A=40°,∠F=20°,
∴△ABC≌△DEF,
∴∠C=∠F=20°,
∴∠B=180°﹣∠A﹣∠C=180°﹣40°﹣20°=120°.
故答案为:120°.
9.【解答】解:∵四边形BEFD是以DE所在直线为对称轴的轴对称图形,四边形CFDE是以FE所在直线为对称轴的轴对称图形,
∴∠EDF=∠C=40°,∠BED=∠DEF=∠CEF,
∵∠BED+∠DEF+∠CEF=180°,
∴∠DEF=60°,
∴∠DFE=180°﹣∠EDF﹣∠DEF=180°﹣40°﹣60°=80°,
故答案为:80°.
10.【解答】解:根据镜面对称性质得出:实际五位数为81088,
故答案为81088.
三、解答题
11.【解答】解:(1)∵点P与点M关于AD对称,点P与点N关于BC对称,
∴EM=EP,FP=FN,
∴C△PEF=PE+PF+EF=ME+EF+FN=MN=12(cm).
(2)∵∠C+∠D=134°,
∴∠A+∠B=360°﹣134°=226°.
又∵PG⊥AD,PH⊥BC,
∴∠PGA=∠PHB=90°,
∴∠HPG=540°﹣90°﹣90°﹣226°=134°.
12.【解答】(1)解:∵点P与点M关于OA对称,
∴ME=PE.
同理:FN=PF.
∴△PEF的周长=EP+FP+EF=ME+EF+FN=MN=15;
(2)证明:∵PN=PM,Q、R为MP,PN的中点,
∴,,
∴PQ=PR.
又∵点P与点M关于OA对称,点P与点N关于OB对称,
∴PQ⊥QA,PR⊥OB,
∴OP平分∠AOB.
13.【解答】解:(1)∵在△ABC中,∠B=50°,∠C=60°,
∴∠A=180°﹣∠B﹣∠C=70°;
(2)∵将△ABC沿着DE折叠压平,A与A′重合,
∴,,
∴∠1+∠2=180°﹣∠AEA′+180°﹣∠ADA′=360°﹣2∠AED﹣2∠ADE,
∵∠AED+∠ADE+∠A=180°,
∴∠AED+∠ADE=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A,
∵∠1+∠2=130°,
∴;
(3)∵将△ABC沿着DE折叠压平,A与A′重合,
∴,,
∴∠1+∠2=180°﹣∠AEA′+180°﹣∠ADA′=360°﹣2∠AED﹣2∠ADE,
∵∠AED+∠ADE+∠A=180°,
∴∠AED+∠ADE=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.
14.【解答】解:(1)∵M,N分别是点O关于PA、PB的对称点,
∴EM=EO,FN=FO,
∴△OEF的周长=OE+OF+EF
=ME+EF+FN=MN
=5(cm);
(2)如图,连接PM,PN,PO,
∵M,N分别是点O关于PA、PB的对称点,
∴∠MPA=∠OPA,∠NPB=∠OPB,
∴∠MPN=2∠APB=2α.
15.【解答】解:(1)∵∠ABC=38°,∠ACD=82°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=30°,
∴∠ADB=∠DAC+∠ACD=30°+82°=112°;
(2)∵△ABH与△AGH关于AH对称
∴△ABH≌△AGH,
∴AB=AG,BH=HG,
∵S△BFH﹣S△AEF=S△ABH﹣S△ABES△ABGS△ABC,
∴S1﹣S2(S△ABG﹣S△ABC)S△BCG,
∵S△BCG=6,
∴S1﹣S2=3.
