9.1.4 设计轴对称图案 培优练习(含答案)
文档属性
| 名称 | 9.1.4 设计轴对称图案 培优练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 865.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 10:34:32 | ||
图片预览



文档简介
9.1.4设计轴对称图案培优练习华东师大版2024—2025学年七年级下册
一、选择题
1.下列各图是中国古典花窗基本图案,其中是轴对称图形的为( )
A. B. C. D.
2.如图,河道l的同侧有M,N两个村庄,计划铺设管道将河水引至M,N两村,下面四个方案中,管道总长度最短的是( )
A.B. C.D.
3.如图,在正方形网格中,M,N为小正方形顶点,直线l经过小正方形顶点A,B,C,D,在直线l上求一点P使PM+PN最短,则点P应位于( )
点A处 B.点B处
C.点C处 D.点D处
4.如图,在△ABC中,AD⊥BC于D点,BE⊥AC于E点,∠ABC=60°,∠BAC=70°,若点P,Q分别是线段AD,AB上的动点,则BP+PQ的最小值与线段( )的长度相等.
A.BD B.AD C.AB D.AC
5.直线l1,l2表示一条河的两岸,且l1∥l2,若村庄P和村庄Q在这条河的两岸.现要在这条河上建一座桥EF(桥EF与河的两岸l1,l2垂直),使得从村庄P经桥EF过河到村庄Q的路径PEFQ最短,即PE+EF+FQ最小.则下列图中满足条件的是( )
A.B. C.D.
二、填空题
6.如图,△ABC的面积为6,AB=5,AD平分∠BAC,若M,N分别是AD,AC上的动点,则MN+CM的最小值为 .
7.如图,在四边形ABCD中,∠B=∠D=90°,∠A=40°,M,N分别是边AB,AD上的动点,当△MCN的周长最小时,∠MCN的大小是 °.
8.如图,△ABC中,AD垂直BC于点D,且AD=BC,BC上方有一动点P满足S△PBCS△ABC,则点P到B、C两点距离之和最小时,∠PBC的度数为 .
9.如图,∠AOB=25°,点M,N分别是边OA,OB上的定点,点P,Q分别是边OB,OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则α与β的数量关系为 .
10.在四边形ABCD中,∠C=50°,∠B=∠D=90°,M,N分别为BC,DC上的点,当△AMN的周长最小时,∠MAN的度数为 .
三、解答题
11.如图,∠ABN=60°,点C为射线BN上一定点,E为线段AB延长线上一定点,且BE=AB=12,点A关于射线BN对称点为D,连接BD,CD,DE.
(1)证明:∠BAC=∠BDC;
(2)若P为直线BC上一个动点,求△PDE周长最小时,P所在的位置,并求出△PDE周长的最小值.
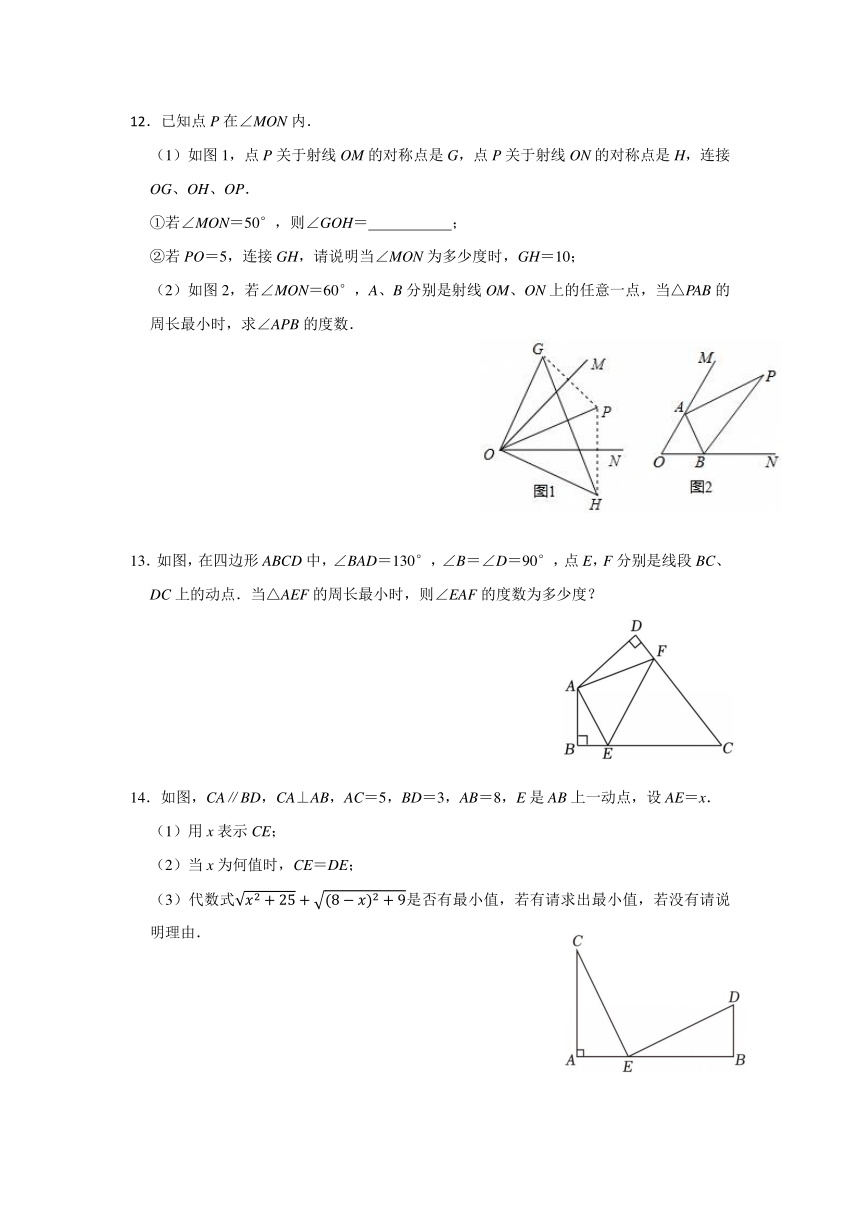
12.已知点P在∠MON内.
(1)如图1,点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG、OH、OP.
①若∠MON=50°,则∠GOH= ;
②若PO=5,连接GH,请说明当∠MON为多少度时,GH=10;
(2)如图2,若∠MON=60°,A、B分别是射线OM、ON上的任意一点,当△PAB的周长最小时,求∠APB的度数.
13.如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC、DC上的动点.当△AEF的周长最小时,则∠EAF的度数为多少度?
14.如图,CA∥BD,CA⊥AB,AC=5,BD=3,AB=8,E是AB上一动点,设AE=x.
(1)用x表示CE;
(2)当x为何值时,CE=DE;
(3)代数式是否有最小值,若有请求出最小值,若没有请说明理由.
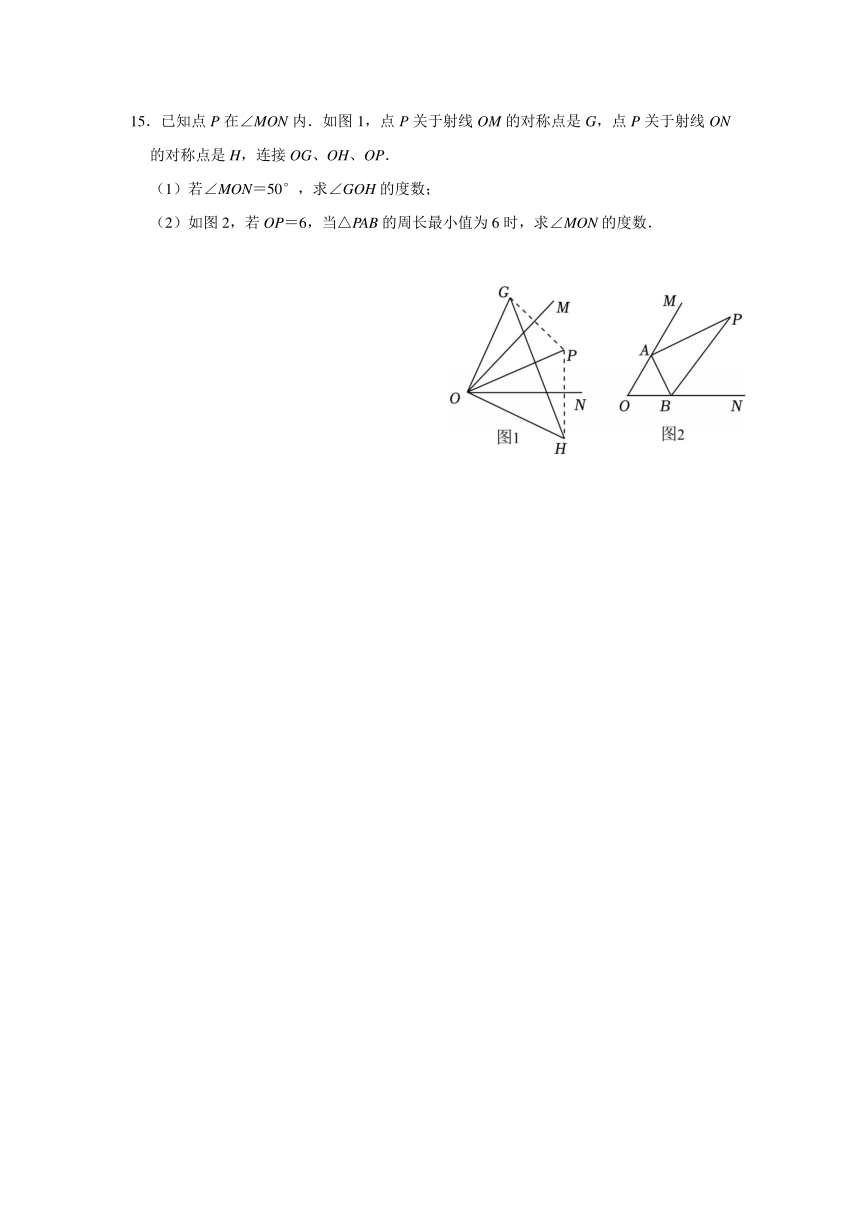
15.已知点P在∠MON内.如图1,点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG、OH、OP.
(1)若∠MON=50°,求∠GOH的度数;
(2)如图2,若OP=6,当△PAB的周长最小值为6时,求∠MON的度数.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C B C B A
二、填空题
6.【解答】解:如图,过点C作CE⊥AB于点E,在AB上截取线段AN′,使得AN′=AN,
∵AD平分∠CAB,AN=AN′,
∴N,N′关于AD对称,
∴MN=MN′,
∴CM+MN=CM+MN′≥CE,
∵S△ABC AB CE,
∴CE,
∴CM+MN,
∴CM+MN的最小值为.
故答案为:.
7.【解答】解:延长CD到E,使得DE=CD,延长CB到F,使得BF=CB,连接EF,交AD,AB于N′,M′,此时△MCN的周长最小,
∵∠B=∠D=90°,
∴AD垂直平分CE,AB垂直平分CF,
∴CN′=EN′,CM′=FM′,
∴∠E=∠ECN′,∠F=∠FCM′,
∵∠B=∠D=90°,∠A=40°,
∴∠ECF=140°,
∴∠E+∠F=40°,
∵∠CN′F+∠CM′E=∠E+∠ECN′+∠F+∠FCM′=2(∠E+∠F)=80°,
∴∠M′CN′=100°,
故答案为:100.
8.【解答】解:∵S△PBCS△ABC,
∴P在与BC平行,且到BC的距离为AD的直线l上,
∴l∥BC,
作点B关于直线l的对称点B',连接B'C交l于P,如图所示:
则BB'⊥l,PB=PB',此时点P到B、C两点距离之和最小,
作PM⊥BC于M,则BB'=2PM=AD,
∵AD⊥BC,AD=BC,
∴BB'=BC,BB'⊥BC,
∴△BB'C是等腰直角三角形,
∴∠B'=45°,
∵PB=PB',
∴∠PBB'=∠B'=45°,
∴∠PBC=90°﹣45°=45°;
故答案为45°.
9.【解答】解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
∴∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∴∠QPN(180°﹣α)=∠AOB+∠MQP=25°(180°﹣β),
∴180°﹣α=50°+(180°﹣β),
∴β﹣α=50°,
故答案为:β﹣α=50°.
10.【解答】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAB=130°,
∴∠HAA′=50°,
∴∠AA′M+∠A″=∠HAA′=50°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×50°=100°,
∴∠MAN=80°,
故答案为:80°.
三、解答题
11.【解答】(1)证明:连接AD,如图,
∵点A关于射线BN对称点为D,
∴BN垂直平分AD,
∴BA=BD,CA=CD,
在△BAC和△BDC中,
,
∴△BAC≌△BDC(SSS),
∴∠BAC=∠BDC;
(2)解:∵△BAC≌△BDC,
∴∠DBN=∠ABN=60°,
∵BE=BA,BA=BD,
∴BE=BD,
∴∠E=∠BDE,
∵∠ABD=∠E+∠BDE,
∴∠E=∠BDE=60°,
∴△BDE为等边三角形,
∴DE=BE=12,
∵BN垂直平分AD,
∴PA=PD,
∴PE+PD=PE+PA,
∵PE+PA≥AE(当且仅当P、A、E共线时取等号),
即点P点运动到B点时,PE+PA的最小值为24,此时△PDE周长的最小值为36.
12.【解答】解:(1)①∵点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,
∴OG=OP,OM⊥GP,
∴OM平分∠POG,
同理可得ON平分∠POH,
∴∠GOH=2∠MON=2×50°=100°,
故答案为:100°;
②∵PO=5,
∴GO=HO=5,
当∠MON=90°时,∠GOH=180°,
∴点G,O,H在同一直线上,
∴GH=GO+HO=10;
(2)如图所示:分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A、B,
连接PA、PB,则AP=AP',BP=BP“,此时△PAB周长的最小值等于P′P″的长.
由轴对称性质可得,OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,
∴∠P′OP″=2∠MON=2×60°=120°,
∴∠OP′P″=∠OP″P′=(180°﹣120°)÷2=30°,
∴∠OPA=∠OP'A=30°,
同理可得∠BPO=∠OP″B=30°,
∴∠APB=30°+30°=60°.
13.【解答】解:作出A关于BC和CD的对称点A′、A″,连接A′A″,交BC于点E,交CD于点F,则A′A″即为△AEF的周长最小值,作DA延长线AH,
∵∠DAB=130°,
∴∠HAA′=50°,
∴∠HAA′=∠AA′E+∠A″=50°,
由折叠可知:AF=A''F,AE=A′E,
∴∠FAD=∠A″,∠EA′A=∠EAA′,
∴∠EAA′+∠A″AF=50°,
∴∠EAF=130°﹣50°=80°.
14.【解答】解:(1)∵CA⊥AB,AC=5,AE=x.
∴;
(2)∵CA∥BD,BD=3,AB=8,
∴BD⊥AB,BE=8﹣x,
∴,
∵CE=DE,
∴x2+25=(8﹣x)2+9,
解得 x=3,
∴当x为3时,CE=DE;
(3)如图,作点C关于直线AB的对称点F,过点F作FG⊥BD交DB的延长线于点G,连接FD,
由对称的性质可得,EC=FE,
∵CA⊥AB,BD⊥AB,
∴∠BAF=∠ABG=∠BGF=90°,
∴四边形AFGB为矩形,
∴BG=AF=AC=5,FG=AB=8,
∴DG=DB+BG=8,
∵,
∴当点D、E、F在同一直线上时,FE+DE的值最小,即CE+DE的值最小,
∴CE+DE的最小值为,
即的最小值为.
15.【解答】解:(1)∵点P关于射线OM的对称点是G,
∴∠GOM=∠POM.
∵点P关于射线ON的对称点是H,
∴∠HON=∠PON.
∵∠MON=∠MOP+∠NOP=50°,
∴∠GOH=∠GOM+∠MOP+∠NOP+∠HON=2∠MON=100°;
(2)作点P关于OM、ON的对称点P′和P″,连接P′P″、OP′、OP″、OP.
∴PA=P′A,PB=P″B,OP′=OP,OP″=OP,∠P′OM=∠POM,∠PON=∠P″ON.
∵△PAB的周长最小值为6,OP=6,
∴P′P″=OP′=OP″=6.
∴△OP′P″为等边三角形.
∴∠P′OP″=60°.
∵∠P′OP″=∠P′OM+∠POM+∠PON+∠P″ON=2∠MON,
∴∠MON=30°.
一、选择题
1.下列各图是中国古典花窗基本图案,其中是轴对称图形的为( )
A. B. C. D.
2.如图,河道l的同侧有M,N两个村庄,计划铺设管道将河水引至M,N两村,下面四个方案中,管道总长度最短的是( )
A.B. C.D.
3.如图,在正方形网格中,M,N为小正方形顶点,直线l经过小正方形顶点A,B,C,D,在直线l上求一点P使PM+PN最短,则点P应位于( )
点A处 B.点B处
C.点C处 D.点D处
4.如图,在△ABC中,AD⊥BC于D点,BE⊥AC于E点,∠ABC=60°,∠BAC=70°,若点P,Q分别是线段AD,AB上的动点,则BP+PQ的最小值与线段( )的长度相等.
A.BD B.AD C.AB D.AC
5.直线l1,l2表示一条河的两岸,且l1∥l2,若村庄P和村庄Q在这条河的两岸.现要在这条河上建一座桥EF(桥EF与河的两岸l1,l2垂直),使得从村庄P经桥EF过河到村庄Q的路径PEFQ最短,即PE+EF+FQ最小.则下列图中满足条件的是( )
A.B. C.D.
二、填空题
6.如图,△ABC的面积为6,AB=5,AD平分∠BAC,若M,N分别是AD,AC上的动点,则MN+CM的最小值为 .
7.如图,在四边形ABCD中,∠B=∠D=90°,∠A=40°,M,N分别是边AB,AD上的动点,当△MCN的周长最小时,∠MCN的大小是 °.
8.如图,△ABC中,AD垂直BC于点D,且AD=BC,BC上方有一动点P满足S△PBCS△ABC,则点P到B、C两点距离之和最小时,∠PBC的度数为 .
9.如图,∠AOB=25°,点M,N分别是边OA,OB上的定点,点P,Q分别是边OB,OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则α与β的数量关系为 .
10.在四边形ABCD中,∠C=50°,∠B=∠D=90°,M,N分别为BC,DC上的点,当△AMN的周长最小时,∠MAN的度数为 .
三、解答题
11.如图,∠ABN=60°,点C为射线BN上一定点,E为线段AB延长线上一定点,且BE=AB=12,点A关于射线BN对称点为D,连接BD,CD,DE.
(1)证明:∠BAC=∠BDC;
(2)若P为直线BC上一个动点,求△PDE周长最小时,P所在的位置,并求出△PDE周长的最小值.
12.已知点P在∠MON内.
(1)如图1,点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG、OH、OP.
①若∠MON=50°,则∠GOH= ;
②若PO=5,连接GH,请说明当∠MON为多少度时,GH=10;
(2)如图2,若∠MON=60°,A、B分别是射线OM、ON上的任意一点,当△PAB的周长最小时,求∠APB的度数.
13.如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC、DC上的动点.当△AEF的周长最小时,则∠EAF的度数为多少度?
14.如图,CA∥BD,CA⊥AB,AC=5,BD=3,AB=8,E是AB上一动点,设AE=x.
(1)用x表示CE;
(2)当x为何值时,CE=DE;
(3)代数式是否有最小值,若有请求出最小值,若没有请说明理由.
15.已知点P在∠MON内.如图1,点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG、OH、OP.
(1)若∠MON=50°,求∠GOH的度数;
(2)如图2,若OP=6,当△PAB的周长最小值为6时,求∠MON的度数.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C B C B A
二、填空题
6.【解答】解:如图,过点C作CE⊥AB于点E,在AB上截取线段AN′,使得AN′=AN,
∵AD平分∠CAB,AN=AN′,
∴N,N′关于AD对称,
∴MN=MN′,
∴CM+MN=CM+MN′≥CE,
∵S△ABC AB CE,
∴CE,
∴CM+MN,
∴CM+MN的最小值为.
故答案为:.
7.【解答】解:延长CD到E,使得DE=CD,延长CB到F,使得BF=CB,连接EF,交AD,AB于N′,M′,此时△MCN的周长最小,
∵∠B=∠D=90°,
∴AD垂直平分CE,AB垂直平分CF,
∴CN′=EN′,CM′=FM′,
∴∠E=∠ECN′,∠F=∠FCM′,
∵∠B=∠D=90°,∠A=40°,
∴∠ECF=140°,
∴∠E+∠F=40°,
∵∠CN′F+∠CM′E=∠E+∠ECN′+∠F+∠FCM′=2(∠E+∠F)=80°,
∴∠M′CN′=100°,
故答案为:100.
8.【解答】解:∵S△PBCS△ABC,
∴P在与BC平行,且到BC的距离为AD的直线l上,
∴l∥BC,
作点B关于直线l的对称点B',连接B'C交l于P,如图所示:
则BB'⊥l,PB=PB',此时点P到B、C两点距离之和最小,
作PM⊥BC于M,则BB'=2PM=AD,
∵AD⊥BC,AD=BC,
∴BB'=BC,BB'⊥BC,
∴△BB'C是等腰直角三角形,
∴∠B'=45°,
∵PB=PB',
∴∠PBB'=∠B'=45°,
∴∠PBC=90°﹣45°=45°;
故答案为45°.
9.【解答】解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
∴∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∴∠QPN(180°﹣α)=∠AOB+∠MQP=25°(180°﹣β),
∴180°﹣α=50°+(180°﹣β),
∴β﹣α=50°,
故答案为:β﹣α=50°.
10.【解答】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAB=130°,
∴∠HAA′=50°,
∴∠AA′M+∠A″=∠HAA′=50°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×50°=100°,
∴∠MAN=80°,
故答案为:80°.
三、解答题
11.【解答】(1)证明:连接AD,如图,
∵点A关于射线BN对称点为D,
∴BN垂直平分AD,
∴BA=BD,CA=CD,
在△BAC和△BDC中,
,
∴△BAC≌△BDC(SSS),
∴∠BAC=∠BDC;
(2)解:∵△BAC≌△BDC,
∴∠DBN=∠ABN=60°,
∵BE=BA,BA=BD,
∴BE=BD,
∴∠E=∠BDE,
∵∠ABD=∠E+∠BDE,
∴∠E=∠BDE=60°,
∴△BDE为等边三角形,
∴DE=BE=12,
∵BN垂直平分AD,
∴PA=PD,
∴PE+PD=PE+PA,
∵PE+PA≥AE(当且仅当P、A、E共线时取等号),
即点P点运动到B点时,PE+PA的最小值为24,此时△PDE周长的最小值为36.
12.【解答】解:(1)①∵点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,
∴OG=OP,OM⊥GP,
∴OM平分∠POG,
同理可得ON平分∠POH,
∴∠GOH=2∠MON=2×50°=100°,
故答案为:100°;
②∵PO=5,
∴GO=HO=5,
当∠MON=90°时,∠GOH=180°,
∴点G,O,H在同一直线上,
∴GH=GO+HO=10;
(2)如图所示:分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A、B,
连接PA、PB,则AP=AP',BP=BP“,此时△PAB周长的最小值等于P′P″的长.
由轴对称性质可得,OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,
∴∠P′OP″=2∠MON=2×60°=120°,
∴∠OP′P″=∠OP″P′=(180°﹣120°)÷2=30°,
∴∠OPA=∠OP'A=30°,
同理可得∠BPO=∠OP″B=30°,
∴∠APB=30°+30°=60°.
13.【解答】解:作出A关于BC和CD的对称点A′、A″,连接A′A″,交BC于点E,交CD于点F,则A′A″即为△AEF的周长最小值,作DA延长线AH,
∵∠DAB=130°,
∴∠HAA′=50°,
∴∠HAA′=∠AA′E+∠A″=50°,
由折叠可知:AF=A''F,AE=A′E,
∴∠FAD=∠A″,∠EA′A=∠EAA′,
∴∠EAA′+∠A″AF=50°,
∴∠EAF=130°﹣50°=80°.
14.【解答】解:(1)∵CA⊥AB,AC=5,AE=x.
∴;
(2)∵CA∥BD,BD=3,AB=8,
∴BD⊥AB,BE=8﹣x,
∴,
∵CE=DE,
∴x2+25=(8﹣x)2+9,
解得 x=3,
∴当x为3时,CE=DE;
(3)如图,作点C关于直线AB的对称点F,过点F作FG⊥BD交DB的延长线于点G,连接FD,
由对称的性质可得,EC=FE,
∵CA⊥AB,BD⊥AB,
∴∠BAF=∠ABG=∠BGF=90°,
∴四边形AFGB为矩形,
∴BG=AF=AC=5,FG=AB=8,
∴DG=DB+BG=8,
∵,
∴当点D、E、F在同一直线上时,FE+DE的值最小,即CE+DE的值最小,
∴CE+DE的最小值为,
即的最小值为.
15.【解答】解:(1)∵点P关于射线OM的对称点是G,
∴∠GOM=∠POM.
∵点P关于射线ON的对称点是H,
∴∠HON=∠PON.
∵∠MON=∠MOP+∠NOP=50°,
∴∠GOH=∠GOM+∠MOP+∠NOP+∠HON=2∠MON=100°;
(2)作点P关于OM、ON的对称点P′和P″,连接P′P″、OP′、OP″、OP.
∴PA=P′A,PB=P″B,OP′=OP,OP″=OP,∠P′OM=∠POM,∠PON=∠P″ON.
∵△PAB的周长最小值为6,OP=6,
∴P′P″=OP′=OP″=6.
∴△OP′P″为等边三角形.
∴∠P′OP″=60°.
∵∠P′OP″=∠P′OM+∠POM+∠PON+∠P″ON=2∠MON,
∴∠MON=30°.
