17.1勾股定理培优练习(含答案)
图片预览

文档简介
17.1勾股定理培优练习人教版2024—2025学年春季八年级下册
一、选择题
1.若直角三角形的两边长为3和4,则第三边长为( )
A.5或 B. C.7 D.5
2.如图,数轴上的点A,点C表示的实数分别是﹣2,1,BC⊥AC于点C,且BC=1,连接AB.若以点A为圆心,AB长为半径画弧交数轴于点A右边的点P,则点P所表示的实数为( )
A. B. C. D.
3.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成.若AB=17,AH=8,则正方形EFGH的边长是( )
A.5 B.6 C.7 D.8
4.赵爽弦图是一个以勾股形之弦为边的正方形.图中包含四个全等的勾股形和一个小正方形,其面积称为朱实和黄实.如图,设每一个勾股形的两条直角边长分别为a和b,若ab=8,且a2+b2=25,则黄实为( )
A.36 B.25 C.16 D.9
5.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以各边为直径作半圆,则图中阴影部分的面积为( )
A.6 B. C.4π﹣6 D.
二、填空题
6.如图,Rt△ABC中,∠C=90°,BC>AC,以AB、BC、AC三边为边长的三个正方形面积分别为S1、S2、S3.若AB=5,S3=5,则S2的值等于 .
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.其中,b+a=12,则中间小正方形的面积是 .
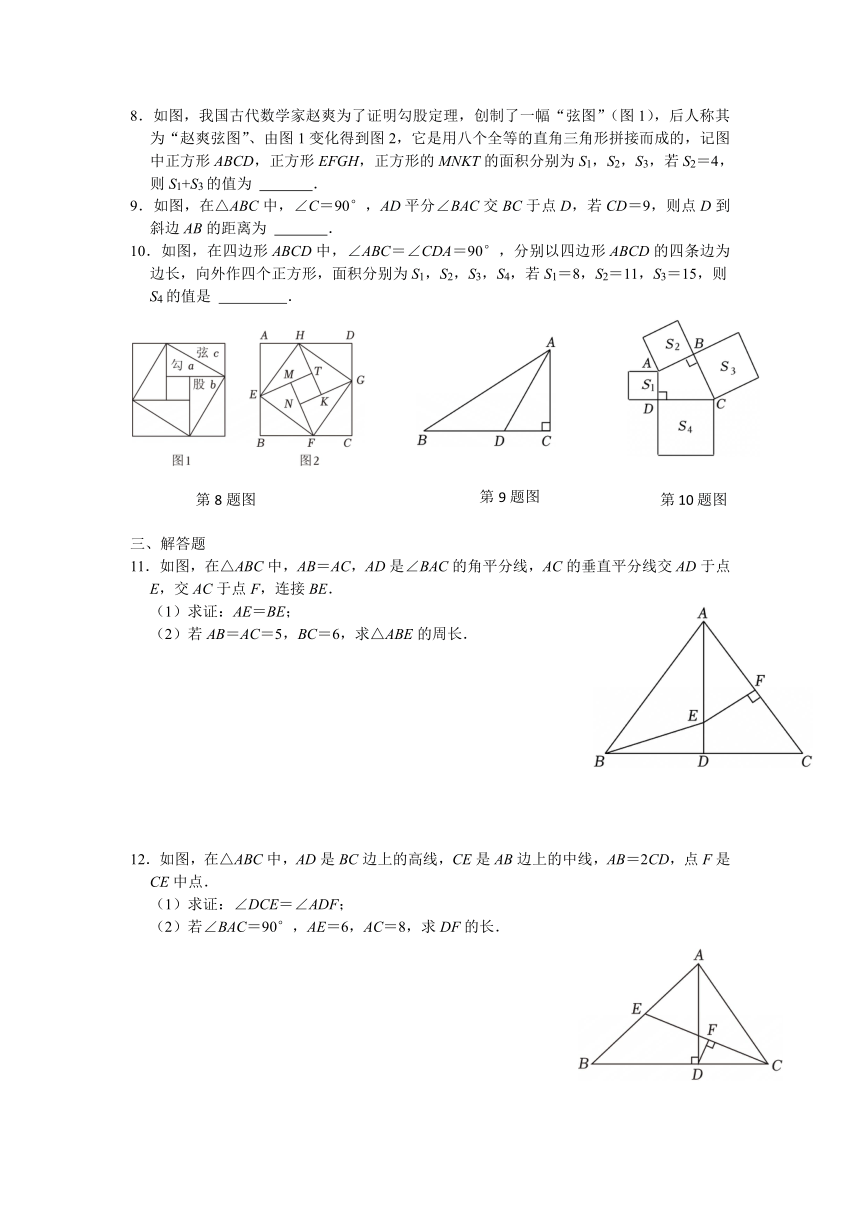
8.如图,我国古代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(图1),后人称其为“赵爽弦图”、由图1变化得到图2,它是用八个全等的直角三角形拼接而成的,记图中正方形ABCD,正方形EFGH,正方形的MNKT的面积分别为S1,S2,S3,若S2=4,则S1+S3的值为 .
9.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=9,则点D到斜边AB的距离为 .
10.如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=8,S2=11,S3=15,则S4的值是 .
三、解答题
11.如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,AC的垂直平分线交AD于点E,交AC于点F,连接BE.
(1)求证:AE=BE;
(2)若AB=AC=5,BC=6,求△ABE的周长.
12.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,AB=2CD,点F是CE中点.
(1)求证:∠DCE=∠ADF;
(2)若∠BAC=90°,AE=6,AC=8,求DF的长.
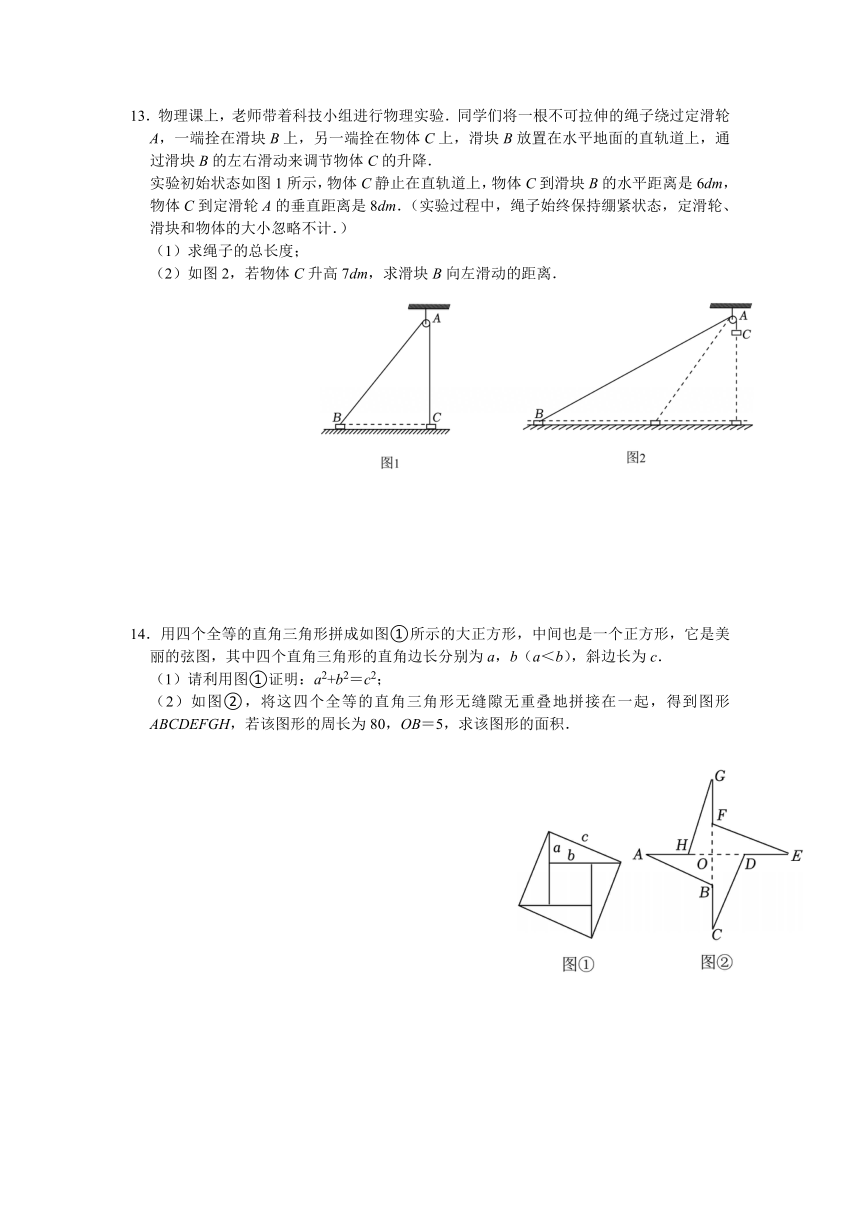
13.物理课上,老师带着科技小组进行物理实验.同学们将一根不可拉伸的绳子绕过定滑轮A,一端拴在滑块B上,另一端拴在物体C上,滑块B放置在水平地面的直轨道上,通过滑块B的左右滑动来调节物体C的升降.
实验初始状态如图1所示,物体C静止在直轨道上,物体C到滑块B的水平距离是6dm,物体C到定滑轮A的垂直距离是8dm.(实验过程中,绳子始终保持绷紧状态,定滑轮、滑块和物体的大小忽略不计.)
(1)求绳子的总长度;
(2)如图2,若物体C升高7dm,求滑块B向左滑动的距离.
14.用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,它是美丽的弦图,其中四个直角三角形的直角边长分别为a,b(a<b),斜边长为c.
(1)请利用图①证明:a2+b2=c2;
(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为80,OB=5,求该图形的面积.
15.如图,在△ABC中,AB=AC,∠BAC为锐角,作AD⊥AB交BC的延长线于点D.
(1)若∠D=20°,求∠BAC的度数.
(2)求证:∠BAC=2∠D.
(3)已知∠D=22.5°,AC,求BC2的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 A A C D A
二、填空题
6.20.
7.36.
8.8.
9.9.
10.18.
三、解答题
11.【解答】(1)证明:连结EC.
∵AB=AC,AD是∠BAC的角平分线,
∴AD垂直平分BC,
∵点E在AD上,
∴BE=EC,
∵AC的垂直平分线交AD于点E,
∴AE=EC,
∴AE=BE.
(2)由(1)得,,
∵BC=6,
∴BD=3,
∴AD4,
设AE=BE=x,
在Rt△BDE中,BD2+DE2=BE2,
∴32+(4﹣x)2=x2,
∴,
即,
∴△ABE的周长为:AB+BE+AE=5.
12.【解答】(1)证明:连结DE,如图,
∵AD是BC边上的高线,
∴∠ADB=∠ADC=90°,
∵CE是AB边上的中线,
∴E是AB边上的中点,
∴AB=2DE,
∵AB=2CD,
∴CD=DE,
∵点F是CE中点,
∴DF⊥EC,
∴∠DFC=90°,
∴∠FDC+∠DCF=90°,
∵∠ADC=90°,
∴∠FDC+∠ADF=90°,
∴∠DCE=∠ADF;
(2)解:∵∠BAC=90°,
在直角三角形ACE中,由勾股定理得:,
∵点F是CE中点,
∴CF=5,
∵∠ADB=90°,E是AB边上的中点,
∴DE=AE=6,
∴CD=DE=6,
∵∠DFC=90°,
在直角三角形CDF中,由勾股定理得:.
13.【解答】解:(1)根据题意得AC=8dm,BC=6dm,∠ACB=90°,
∴AB10(dm),
∴AB+AC=10+8=18(dm),
答:绳子的总长度为18dm;
(2)如图,
根据题意得∠ADB=90°,AD=8dm,CD=7dm,AB=(10+7)dm,
∴15(dm),
∴BE=BD﹣DE=15﹣6=9(dm),
答:滑块B向左滑动的距离为9dm.
14.【解答】(1)证明:S小正方形=(b﹣a)2=a2﹣2ab+b2,
S小正方形=c2﹣4ab=c2﹣2ab,
即b2﹣2ab+a2=c2﹣2ab,
∴a2+b2=c2;
(2)解:∵AB+BC=80÷4=20,
设AH=BC=x,则AB=20﹣x,OH=OB=5,
在Rt△AOB中,由勾股定理得:
OH2+OG2=GH2,
即52+(5+x)2=(20﹣x)2,
解得:x=7,
∴S5×12×4=120.
15.【解答】(1)解:∵AD⊥AB,
∴∠B+∠D=90°.
∵∠D=20°,
∴∠B=90°﹣20°=70°.
∵AB=AC,
∴∠ACB=∠B=70°,
∴∠BAC=180°﹣2×70°=40°.
(2)证明:∵AD⊥AB,
∴∠B+∠D=90°.,
即∠B=90°﹣∠D.
∵AB=AC,
∴∠B=∠ACB,
∴∠BAC=180°﹣2∠B,
即∠B=90°∠BAC,
∴90°﹣∠D=90°∠BAC,
∴∠BAC=2∠D.
(3)解:过点C作AB的垂线,垂足为M,
∵∠D=22.5°,
∴∠BAC=2×22.5°=45°,
∴△AMC是等腰直角三角形.
∵AC,
∴AM=MC=1.
∵AB=AC,
∴BM.
在Rt△BCM中,
BC2=BM2+MC2=()2+12=4.
一、选择题
1.若直角三角形的两边长为3和4,则第三边长为( )
A.5或 B. C.7 D.5
2.如图,数轴上的点A,点C表示的实数分别是﹣2,1,BC⊥AC于点C,且BC=1,连接AB.若以点A为圆心,AB长为半径画弧交数轴于点A右边的点P,则点P所表示的实数为( )
A. B. C. D.
3.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成.若AB=17,AH=8,则正方形EFGH的边长是( )
A.5 B.6 C.7 D.8
4.赵爽弦图是一个以勾股形之弦为边的正方形.图中包含四个全等的勾股形和一个小正方形,其面积称为朱实和黄实.如图,设每一个勾股形的两条直角边长分别为a和b,若ab=8,且a2+b2=25,则黄实为( )
A.36 B.25 C.16 D.9
5.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以各边为直径作半圆,则图中阴影部分的面积为( )
A.6 B. C.4π﹣6 D.
二、填空题
6.如图,Rt△ABC中,∠C=90°,BC>AC,以AB、BC、AC三边为边长的三个正方形面积分别为S1、S2、S3.若AB=5,S3=5,则S2的值等于 .
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.其中,b+a=12,则中间小正方形的面积是 .
8.如图,我国古代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(图1),后人称其为“赵爽弦图”、由图1变化得到图2,它是用八个全等的直角三角形拼接而成的,记图中正方形ABCD,正方形EFGH,正方形的MNKT的面积分别为S1,S2,S3,若S2=4,则S1+S3的值为 .
9.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=9,则点D到斜边AB的距离为 .
10.如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=8,S2=11,S3=15,则S4的值是 .
三、解答题
11.如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,AC的垂直平分线交AD于点E,交AC于点F,连接BE.
(1)求证:AE=BE;
(2)若AB=AC=5,BC=6,求△ABE的周长.
12.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,AB=2CD,点F是CE中点.
(1)求证:∠DCE=∠ADF;
(2)若∠BAC=90°,AE=6,AC=8,求DF的长.
13.物理课上,老师带着科技小组进行物理实验.同学们将一根不可拉伸的绳子绕过定滑轮A,一端拴在滑块B上,另一端拴在物体C上,滑块B放置在水平地面的直轨道上,通过滑块B的左右滑动来调节物体C的升降.
实验初始状态如图1所示,物体C静止在直轨道上,物体C到滑块B的水平距离是6dm,物体C到定滑轮A的垂直距离是8dm.(实验过程中,绳子始终保持绷紧状态,定滑轮、滑块和物体的大小忽略不计.)
(1)求绳子的总长度;
(2)如图2,若物体C升高7dm,求滑块B向左滑动的距离.
14.用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,它是美丽的弦图,其中四个直角三角形的直角边长分别为a,b(a<b),斜边长为c.
(1)请利用图①证明:a2+b2=c2;
(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为80,OB=5,求该图形的面积.
15.如图,在△ABC中,AB=AC,∠BAC为锐角,作AD⊥AB交BC的延长线于点D.
(1)若∠D=20°,求∠BAC的度数.
(2)求证:∠BAC=2∠D.
(3)已知∠D=22.5°,AC,求BC2的值.
参考答案
一、选择题
题号 1 2 3 4 5
答案 A A C D A
二、填空题
6.20.
7.36.
8.8.
9.9.
10.18.
三、解答题
11.【解答】(1)证明:连结EC.
∵AB=AC,AD是∠BAC的角平分线,
∴AD垂直平分BC,
∵点E在AD上,
∴BE=EC,
∵AC的垂直平分线交AD于点E,
∴AE=EC,
∴AE=BE.
(2)由(1)得,,
∵BC=6,
∴BD=3,
∴AD4,
设AE=BE=x,
在Rt△BDE中,BD2+DE2=BE2,
∴32+(4﹣x)2=x2,
∴,
即,
∴△ABE的周长为:AB+BE+AE=5.
12.【解答】(1)证明:连结DE,如图,
∵AD是BC边上的高线,
∴∠ADB=∠ADC=90°,
∵CE是AB边上的中线,
∴E是AB边上的中点,
∴AB=2DE,
∵AB=2CD,
∴CD=DE,
∵点F是CE中点,
∴DF⊥EC,
∴∠DFC=90°,
∴∠FDC+∠DCF=90°,
∵∠ADC=90°,
∴∠FDC+∠ADF=90°,
∴∠DCE=∠ADF;
(2)解:∵∠BAC=90°,
在直角三角形ACE中,由勾股定理得:,
∵点F是CE中点,
∴CF=5,
∵∠ADB=90°,E是AB边上的中点,
∴DE=AE=6,
∴CD=DE=6,
∵∠DFC=90°,
在直角三角形CDF中,由勾股定理得:.
13.【解答】解:(1)根据题意得AC=8dm,BC=6dm,∠ACB=90°,
∴AB10(dm),
∴AB+AC=10+8=18(dm),
答:绳子的总长度为18dm;
(2)如图,
根据题意得∠ADB=90°,AD=8dm,CD=7dm,AB=(10+7)dm,
∴15(dm),
∴BE=BD﹣DE=15﹣6=9(dm),
答:滑块B向左滑动的距离为9dm.
14.【解答】(1)证明:S小正方形=(b﹣a)2=a2﹣2ab+b2,
S小正方形=c2﹣4ab=c2﹣2ab,
即b2﹣2ab+a2=c2﹣2ab,
∴a2+b2=c2;
(2)解:∵AB+BC=80÷4=20,
设AH=BC=x,则AB=20﹣x,OH=OB=5,
在Rt△AOB中,由勾股定理得:
OH2+OG2=GH2,
即52+(5+x)2=(20﹣x)2,
解得:x=7,
∴S5×12×4=120.
15.【解答】(1)解:∵AD⊥AB,
∴∠B+∠D=90°.
∵∠D=20°,
∴∠B=90°﹣20°=70°.
∵AB=AC,
∴∠ACB=∠B=70°,
∴∠BAC=180°﹣2×70°=40°.
(2)证明:∵AD⊥AB,
∴∠B+∠D=90°.,
即∠B=90°﹣∠D.
∵AB=AC,
∴∠B=∠ACB,
∴∠BAC=180°﹣2∠B,
即∠B=90°∠BAC,
∴90°﹣∠D=90°∠BAC,
∴∠BAC=2∠D.
(3)解:过点C作AB的垂线,垂足为M,
∵∠D=22.5°,
∴∠BAC=2×22.5°=45°,
∴△AMC是等腰直角三角形.
∵AC,
∴AM=MC=1.
∵AB=AC,
∴BM.
在Rt△BCM中,
BC2=BM2+MC2=()2+12=4.
