18.1.2平行四边形的判定培优练习(含答案)
文档属性
| 名称 | 18.1.2平行四边形的判定培优练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 617.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 17:53:21 | ||
图片预览



文档简介
18.1.2平行四边形的判定培优练习人教版2024—2025学年八年级下册
一、选择题
1.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点.以这些点为顶点,在图中,能画出平行四边形的个数最多为( )
A.1 B.2 C.3 D.4
2.如图,四边形ABCD的对角线相交于点O,下列条件能判定四边形ABCD是平行四边形的是( )
A.AD=BC,OB=OD B.AB=CD,AC=BD
C.AB∥CD,OA=OC D.AB=CD,BC∥AD
3.下面判定四边形是平行四边形的方法中,错误的是( )
A.一组对边平行,另一组对边也平行的四边形是平行四边形
B.一组对角相等,另一组对角也相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行,另一组对边相等的四边形是平行四边形
4.如图,在腰长为8的等腰△ABC中,AB=AC,E,M,F分别是AB,BC,AC上的点,并且ME∥AC,MF∥AB,则四边形MEAF的周长是( )
A.8 B.10 C.12 D.16
5.如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,连接AC、BD,直线EF经过AC、BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:①BO=OD;②△AOD的周长﹣△ODC的周长=AD﹣CD;③AD∥BC;④图中全等的三角形的对数是9对;其中正确结论的个数是( )
A.①③ B.①②③ C.①③④ D.①②④
二、填空题
6.△ABC中,D、E分别为AB、AC中点,延长DE到F,使EF=DE,AB=12,BC=10,则四边形BCFD的周长为 .
7.如图,四边形ABCD中,AB∥CD,AB=6,DC=13,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是 .
8.如图,平行四边形ABCD的对角线AC,BD相交于点O,E、F是对角线AC上的两点,给出下列4个条件:①OE=OF;②DE=BF;③∠ADE=∠BCF;④∠ABE=∠CDF;其中不能判定四边形DEBF是平行四边形的是 .(只填序号)
9.在四边形ABCD中,AB=CD,AD=BC,∠A=55°,则∠C= .
10.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,CE,则下列结论:①△ABD≌△ACE;②四边形BDEF是平行四边形;③S四边形BDEF;④S△AEF.其中正确的为 (只填序号)
三、解答题
11.如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE.
(1)求证:四边形ADCF是平行四边形;
(2)求证:.
12.已知:如图,在平行四边形ABCD中,对角线BD,AC相交于点O,点E,F分别在BD,DB的延长线上,且DE=BF,连接AE,AF,CF,CE.
(1)求证:四边形AFCE为平行四边形;
(2)若AC平分∠EAF,∠AEC=60°,OA=4,求四边形AFCE的周长.
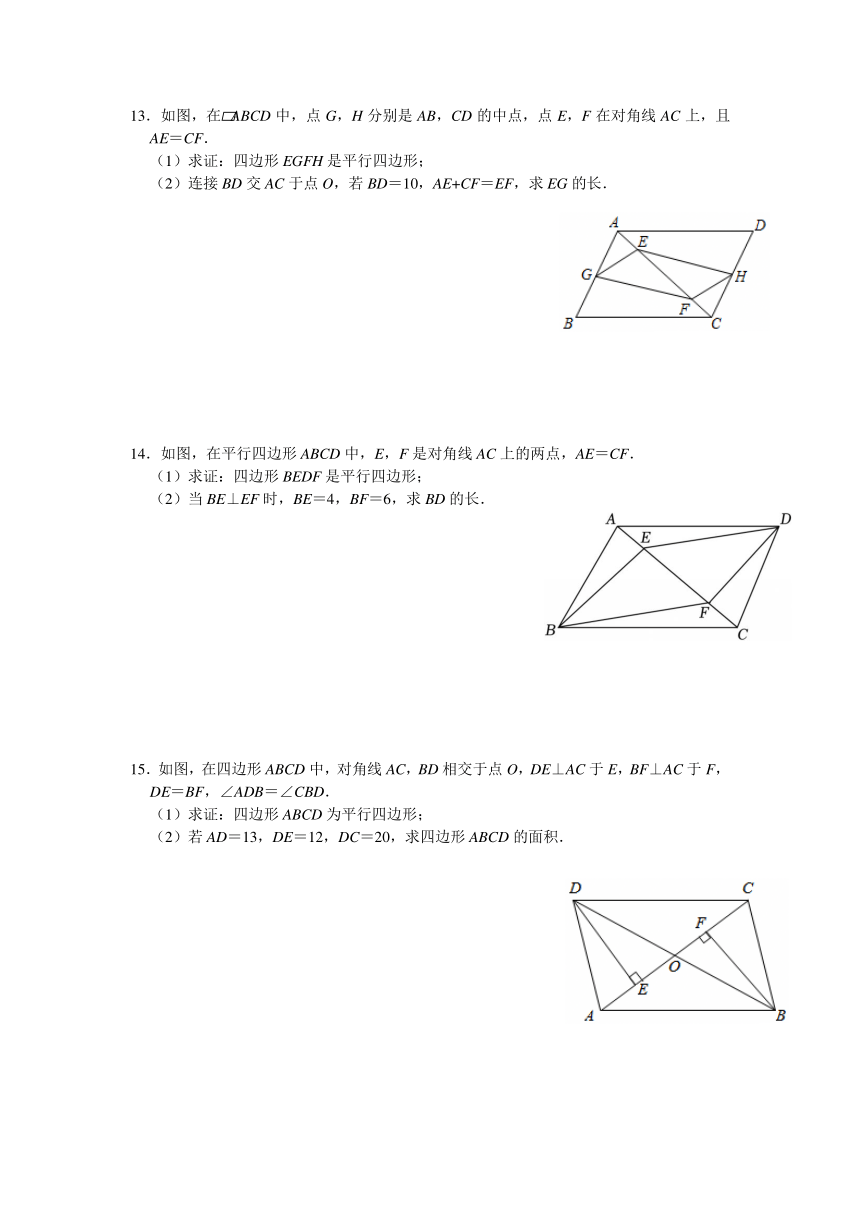
13.如图,在 ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=10,AE+CF=EF,求EG的长.
14.如图,在平行四边形ABCD中,E,F是对角线AC上的两点,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)当BE⊥EF时,BE=4,BF=6,求BD的长.
15.如图,在四边形ABCD中,对角线AC,BD相交于点O,DE⊥AC于E,BF⊥AC于F,DE=BF,∠ADB=∠CBD.
(1)求证:四边形ABCD为平行四边形;
(2)若AD=13,DE=12,DC=20,求四边形ABCD的面积.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C C D D B
二、填空题
6.【解答】解:∵D、E分别为AB、AC中点,
∴DEBC,
∵BC=10,
∴DE=5,
∵在△ADE和△CFE中,
,
∴△ADE≌△CFE,
∴CF=BDAB=6,
∵DE=FE=5,
∴DF=10,
∴四边形BCFD的周长为:BD+BC+CF+DF=6+10+6+10=32,
故答案为:32.
7.【解答】解:过点B作BH∥AC,交DC的延长线于点H,取BH的中点I,连接FI.
∵在△ACD中,点F、G分别是AC、DC的中点,
∴FG∥AD,,
∵在△BCD中,点E、G分别是BD、DC的中点,
∴EG∥BC,,
∴,
∵AB∥DC,点H在DC的延长线上,
∴AB∥CH,且BH∥AC,
∴四边形ABHC是平行四边形,
∴AB=CH=6,
∴DH=DC+CH=13+6=19,AC=BH,
∵点F是AC的中点,点I是BH的中点,
∴,,
∴BI=AF,BI∥AF,
∴四边形BIFA是平行四边形,
∴AB∥FI,
∵AB∥DC,
∴FI∥CD,
∵点E是BD的中点,点I是BH的中点,
∴EI∥DH,,
∴,点E,F,I三点共线,
∴.
故答案为:.
8.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD∥BC,AD=BC,OB=OD,OA=OC,
①OE=OF,
则四边形DEBF是平行四边形;
故①能判定四边形DEBF是平行四边形;
②DE=BF时,不能证明OE=OF,
故②不能判定四边形DEBF是平行四边形;
③∠ADE=∠BCF时,不能证明OE=OF,
故③不能判定四边形DEBF是平行四边形;
④∵AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(ASA),
∴AE=CF,
∴OA﹣AE=OC﹣CF,即OE=OF,
又∵OB=OD,
∴四边形DEBF是平行四边形;
故④能判定四边形DEBF是平行四边形;
故答案为:②③.
9.【解答】解:由题意可知∵AB=CD,AD=BC,
∴ABCD为平行四边形(两组对边分别相等的四边形),
∵∠A=55°,
∴∠A=∠C=55°,
故答案为:55°.
10.【解答】解:连接EC,作CH⊥EF于H.
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠ABC=∠ACB=60°,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=EC=1,∠ACE=∠ABD=60°,
∵EF∥BC,
∴∠EFC=∠ACB=60°,
∴△EFC是等边三角形,
∴CH,EF=EC=BD,
∵EF∥BD,
∴四边形BDEF是平行四边形,
故②正确,
∵BD=CF=1,BA=BC,∠ABD=∠BCF,
∴△ABD≌△BCF(SAS),
故①正确,
∵S平行四边形BDEF=BD CH,
故③正确,
∵AC=BC=3,BD=CF=1,
∴CD=2BD,AF=2CF,
∵S△ABD1,
∴S△AEF S△AEC S△ABD,
故④错误,
∴①②③都正确,
故答案为:①②③.
三、解答题
11.【解答】证明:(1)∵E是AC的中点,
∴AE=CE,
∵F是DE延长线上的点,且EF=DE,
∴四边形ADCF是平行四边形.
(2)∵D是AB的中点,
∴AD=BD,
∵四边形ADCF是平行四边形,
∴AD∥CF,且AD=CF,
∴BD∥CF,且BD=CF,
∴四边形BDFC是平行四边形,
∴DF=BC,
∵EF=DEDF,
∴DEBC.
12.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴OD=OB,
∵DE=BF,
∴OD+DE=OB+BF,
∴OE=OF,
∵OA=OC,
∴四边形AFCE为平行四边形.
(2)解:∵AC平分∠EAF,
∴∠EAC=∠FAC,
∵四边形AFCE为平行四边形,OA=4,
∴CE∥AF,OC=OA=4,
∴∠ECA=∠FAC,AC=4+4=8,
∴∠EAC=∠ECA,
∴AE=CE,
∴四边形AFCE是菱形,
∵∠AEC=60°,
∴△EAC是等边三角形,
∴AE=AC=8,
∴AF+CF+CE+AE=4AE=4×8=32,
∴四边形AFCE周长是32.
13.【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
∵AE=CF,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=10,
∴OB=OD=5,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EGOB=2.5.
∴EG的长为2.5.
14.【解答】(1)证明:如图,连接BD交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形BEDF是平行四边形;
(2)解:∵BE⊥EF,
∴∠BEF=90°,
∴EF,
∵BE=4,BF=6,
∴EF2,
由(1)可知,OE=OF,OB=OD,
∴OE=OFEF,
∴OB,
∴BD=2OB=2,
即BD的长为2.
15.【解答】(1)证明:∵∠ADB=∠CBD,
∴AD∥BC,
∴∠DAE=∠BCF,
∵DE⊥AC于E,BF⊥AC于F,
∴∠DEA=∠BFC=90°,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(AAS),
∴AD=BC,
∴四边形ABCD为平行四边形;
(2)解:在Rt△ADE中,∵AD=13,DE=12,
∴AE5,
在Rt△CDE中,∵DE=12,DC=20,
∴CE16,
∴AC=5+16=21,
∴四边形ABCD的面积=2S△ACD=221×12=252.
一、选择题
1.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点.以这些点为顶点,在图中,能画出平行四边形的个数最多为( )
A.1 B.2 C.3 D.4
2.如图,四边形ABCD的对角线相交于点O,下列条件能判定四边形ABCD是平行四边形的是( )
A.AD=BC,OB=OD B.AB=CD,AC=BD
C.AB∥CD,OA=OC D.AB=CD,BC∥AD
3.下面判定四边形是平行四边形的方法中,错误的是( )
A.一组对边平行,另一组对边也平行的四边形是平行四边形
B.一组对角相等,另一组对角也相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行,另一组对边相等的四边形是平行四边形
4.如图,在腰长为8的等腰△ABC中,AB=AC,E,M,F分别是AB,BC,AC上的点,并且ME∥AC,MF∥AB,则四边形MEAF的周长是( )
A.8 B.10 C.12 D.16
5.如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,连接AC、BD,直线EF经过AC、BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:①BO=OD;②△AOD的周长﹣△ODC的周长=AD﹣CD;③AD∥BC;④图中全等的三角形的对数是9对;其中正确结论的个数是( )
A.①③ B.①②③ C.①③④ D.①②④
二、填空题
6.△ABC中,D、E分别为AB、AC中点,延长DE到F,使EF=DE,AB=12,BC=10,则四边形BCFD的周长为 .
7.如图,四边形ABCD中,AB∥CD,AB=6,DC=13,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是 .
8.如图,平行四边形ABCD的对角线AC,BD相交于点O,E、F是对角线AC上的两点,给出下列4个条件:①OE=OF;②DE=BF;③∠ADE=∠BCF;④∠ABE=∠CDF;其中不能判定四边形DEBF是平行四边形的是 .(只填序号)
9.在四边形ABCD中,AB=CD,AD=BC,∠A=55°,则∠C= .
10.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,CE,则下列结论:①△ABD≌△ACE;②四边形BDEF是平行四边形;③S四边形BDEF;④S△AEF.其中正确的为 (只填序号)
三、解答题
11.如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE.
(1)求证:四边形ADCF是平行四边形;
(2)求证:.
12.已知:如图,在平行四边形ABCD中,对角线BD,AC相交于点O,点E,F分别在BD,DB的延长线上,且DE=BF,连接AE,AF,CF,CE.
(1)求证:四边形AFCE为平行四边形;
(2)若AC平分∠EAF,∠AEC=60°,OA=4,求四边形AFCE的周长.
13.如图,在 ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=10,AE+CF=EF,求EG的长.
14.如图,在平行四边形ABCD中,E,F是对角线AC上的两点,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)当BE⊥EF时,BE=4,BF=6,求BD的长.
15.如图,在四边形ABCD中,对角线AC,BD相交于点O,DE⊥AC于E,BF⊥AC于F,DE=BF,∠ADB=∠CBD.
(1)求证:四边形ABCD为平行四边形;
(2)若AD=13,DE=12,DC=20,求四边形ABCD的面积.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C C D D B
二、填空题
6.【解答】解:∵D、E分别为AB、AC中点,
∴DEBC,
∵BC=10,
∴DE=5,
∵在△ADE和△CFE中,
,
∴△ADE≌△CFE,
∴CF=BDAB=6,
∵DE=FE=5,
∴DF=10,
∴四边形BCFD的周长为:BD+BC+CF+DF=6+10+6+10=32,
故答案为:32.
7.【解答】解:过点B作BH∥AC,交DC的延长线于点H,取BH的中点I,连接FI.
∵在△ACD中,点F、G分别是AC、DC的中点,
∴FG∥AD,,
∵在△BCD中,点E、G分别是BD、DC的中点,
∴EG∥BC,,
∴,
∵AB∥DC,点H在DC的延长线上,
∴AB∥CH,且BH∥AC,
∴四边形ABHC是平行四边形,
∴AB=CH=6,
∴DH=DC+CH=13+6=19,AC=BH,
∵点F是AC的中点,点I是BH的中点,
∴,,
∴BI=AF,BI∥AF,
∴四边形BIFA是平行四边形,
∴AB∥FI,
∵AB∥DC,
∴FI∥CD,
∵点E是BD的中点,点I是BH的中点,
∴EI∥DH,,
∴,点E,F,I三点共线,
∴.
故答案为:.
8.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD∥BC,AD=BC,OB=OD,OA=OC,
①OE=OF,
则四边形DEBF是平行四边形;
故①能判定四边形DEBF是平行四边形;
②DE=BF时,不能证明OE=OF,
故②不能判定四边形DEBF是平行四边形;
③∠ADE=∠BCF时,不能证明OE=OF,
故③不能判定四边形DEBF是平行四边形;
④∵AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(ASA),
∴AE=CF,
∴OA﹣AE=OC﹣CF,即OE=OF,
又∵OB=OD,
∴四边形DEBF是平行四边形;
故④能判定四边形DEBF是平行四边形;
故答案为:②③.
9.【解答】解:由题意可知∵AB=CD,AD=BC,
∴ABCD为平行四边形(两组对边分别相等的四边形),
∵∠A=55°,
∴∠A=∠C=55°,
故答案为:55°.
10.【解答】解:连接EC,作CH⊥EF于H.
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠ABC=∠ACB=60°,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=EC=1,∠ACE=∠ABD=60°,
∵EF∥BC,
∴∠EFC=∠ACB=60°,
∴△EFC是等边三角形,
∴CH,EF=EC=BD,
∵EF∥BD,
∴四边形BDEF是平行四边形,
故②正确,
∵BD=CF=1,BA=BC,∠ABD=∠BCF,
∴△ABD≌△BCF(SAS),
故①正确,
∵S平行四边形BDEF=BD CH,
故③正确,
∵AC=BC=3,BD=CF=1,
∴CD=2BD,AF=2CF,
∵S△ABD1,
∴S△AEF S△AEC S△ABD,
故④错误,
∴①②③都正确,
故答案为:①②③.
三、解答题
11.【解答】证明:(1)∵E是AC的中点,
∴AE=CE,
∵F是DE延长线上的点,且EF=DE,
∴四边形ADCF是平行四边形.
(2)∵D是AB的中点,
∴AD=BD,
∵四边形ADCF是平行四边形,
∴AD∥CF,且AD=CF,
∴BD∥CF,且BD=CF,
∴四边形BDFC是平行四边形,
∴DF=BC,
∵EF=DEDF,
∴DEBC.
12.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴OD=OB,
∵DE=BF,
∴OD+DE=OB+BF,
∴OE=OF,
∵OA=OC,
∴四边形AFCE为平行四边形.
(2)解:∵AC平分∠EAF,
∴∠EAC=∠FAC,
∵四边形AFCE为平行四边形,OA=4,
∴CE∥AF,OC=OA=4,
∴∠ECA=∠FAC,AC=4+4=8,
∴∠EAC=∠ECA,
∴AE=CE,
∴四边形AFCE是菱形,
∵∠AEC=60°,
∴△EAC是等边三角形,
∴AE=AC=8,
∴AF+CF+CE+AE=4AE=4×8=32,
∴四边形AFCE周长是32.
13.【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
∵AE=CF,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=10,
∴OB=OD=5,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EGOB=2.5.
∴EG的长为2.5.
14.【解答】(1)证明:如图,连接BD交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形BEDF是平行四边形;
(2)解:∵BE⊥EF,
∴∠BEF=90°,
∴EF,
∵BE=4,BF=6,
∴EF2,
由(1)可知,OE=OF,OB=OD,
∴OE=OFEF,
∴OB,
∴BD=2OB=2,
即BD的长为2.
15.【解答】(1)证明:∵∠ADB=∠CBD,
∴AD∥BC,
∴∠DAE=∠BCF,
∵DE⊥AC于E,BF⊥AC于F,
∴∠DEA=∠BFC=90°,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(AAS),
∴AD=BC,
∴四边形ABCD为平行四边形;
(2)解:在Rt△ADE中,∵AD=13,DE=12,
∴AE5,
在Rt△CDE中,∵DE=12,DC=20,
∴CE16,
∴AC=5+16=21,
∴四边形ABCD的面积=2S△ACD=221×12=252.
