18.2.2菱形培优练习(含答案)
图片预览

文档简介
18.2.2菱形培优练习人教版2024—2025学年春季八年级下册
一、选择题
1.在下列条件中选取一个作为增加条件,能使 ABCD成为菱形的是( )
A.AC=BD B.AB=DC C.AC⊥BD D.AD∥BC
2.依据所标数据,下列四边形不一定为菱形的是( )
A. B. C. D.
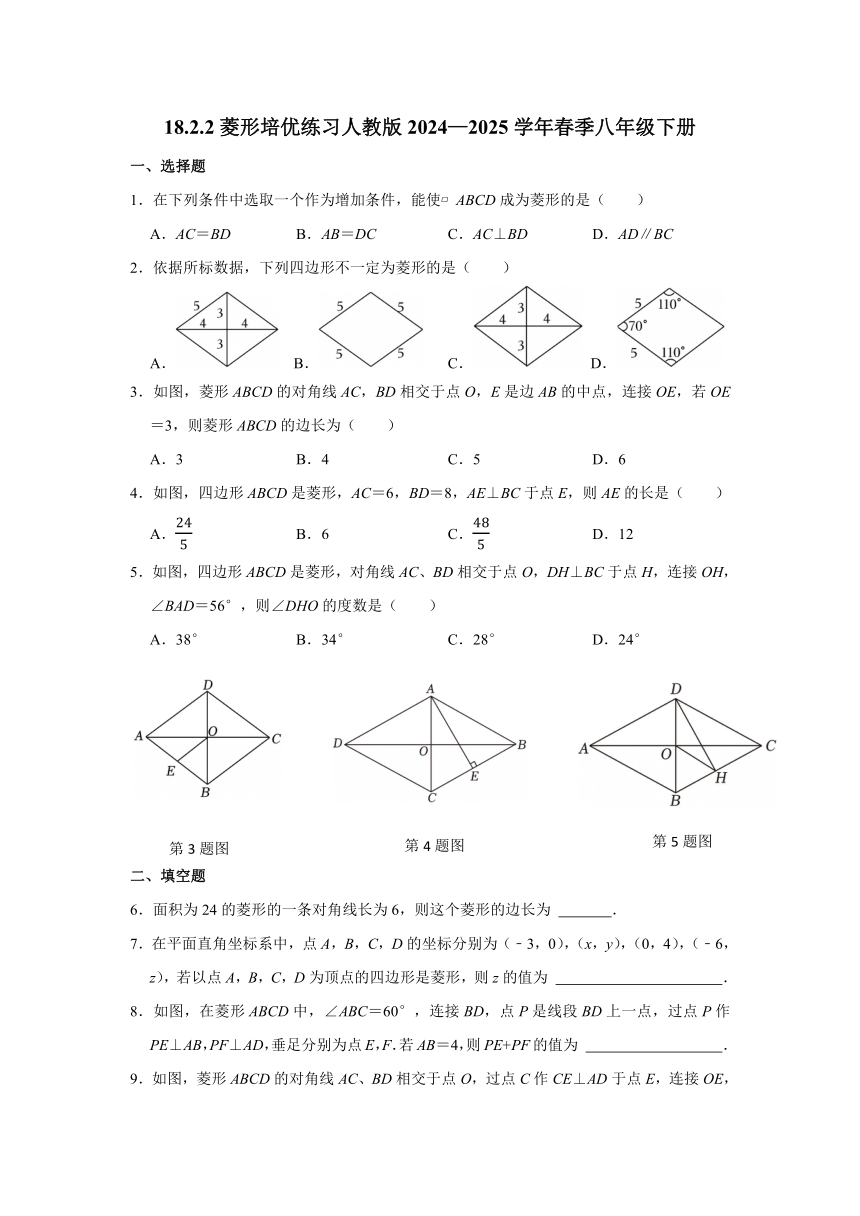
3.如图,菱形ABCD的对角线AC,BD相交于点O,E是边AB的中点,连接OE,若OE=3,则菱形ABCD的边长为( )
A.3 B.4 C.5 D.6
4.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
5.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥BC于点H,连接OH,∠BAD=56°,则∠DHO的度数是( )
A.38° B.34° C.28° D.24°
二、填空题
6.面积为24的菱形的一条对角线长为6,则这个菱形的边长为 .
7.在平面直角坐标系中,点A,B,C,D的坐标分别为(﹣3,0),(x,y),(0,4),(﹣6,z),若以点A,B,C,D为顶点的四边形是菱形,则z的值为 .
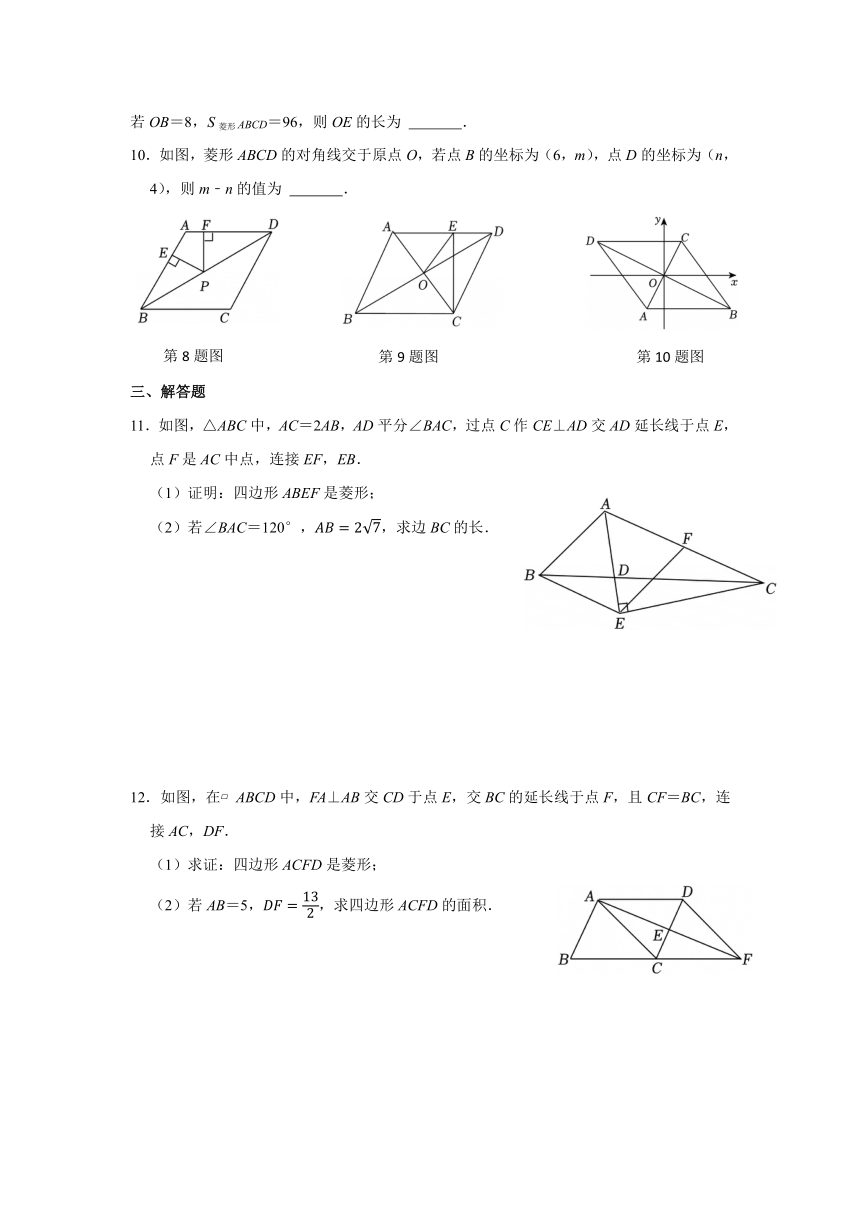
8.如图,在菱形ABCD中,∠ABC=60°,连接BD,点P是线段BD上一点,过点P作PE⊥AB,PF⊥AD,垂足分别为点E,F.若AB=4,则PE+PF的值为 .
9.如图,菱形ABCD的对角线AC、BD相交于点O,过点C作CE⊥AD于点E,连接OE,若OB=8,S菱形ABCD=96,则OE的长为 .
10.如图,菱形ABCD的对角线交于原点O,若点B的坐标为(6,m),点D的坐标为(n,4),则m﹣n的值为 .
三、解答题
11.如图,△ABC中,AC=2AB,AD平分∠BAC,过点C作CE⊥AD交AD延长线于点E,点F是AC中点,连接EF,EB.
(1)证明:四边形ABEF是菱形;
(2)若∠BAC=120°,,求边BC的长.
12.如图,在 ABCD中,FA⊥AB交CD于点E,交BC的延长线于点F,且CF=BC,连接AC,DF.
(1)求证:四边形ACFD是菱形;
(2)若AB=5,,求四边形ACFD的面积.
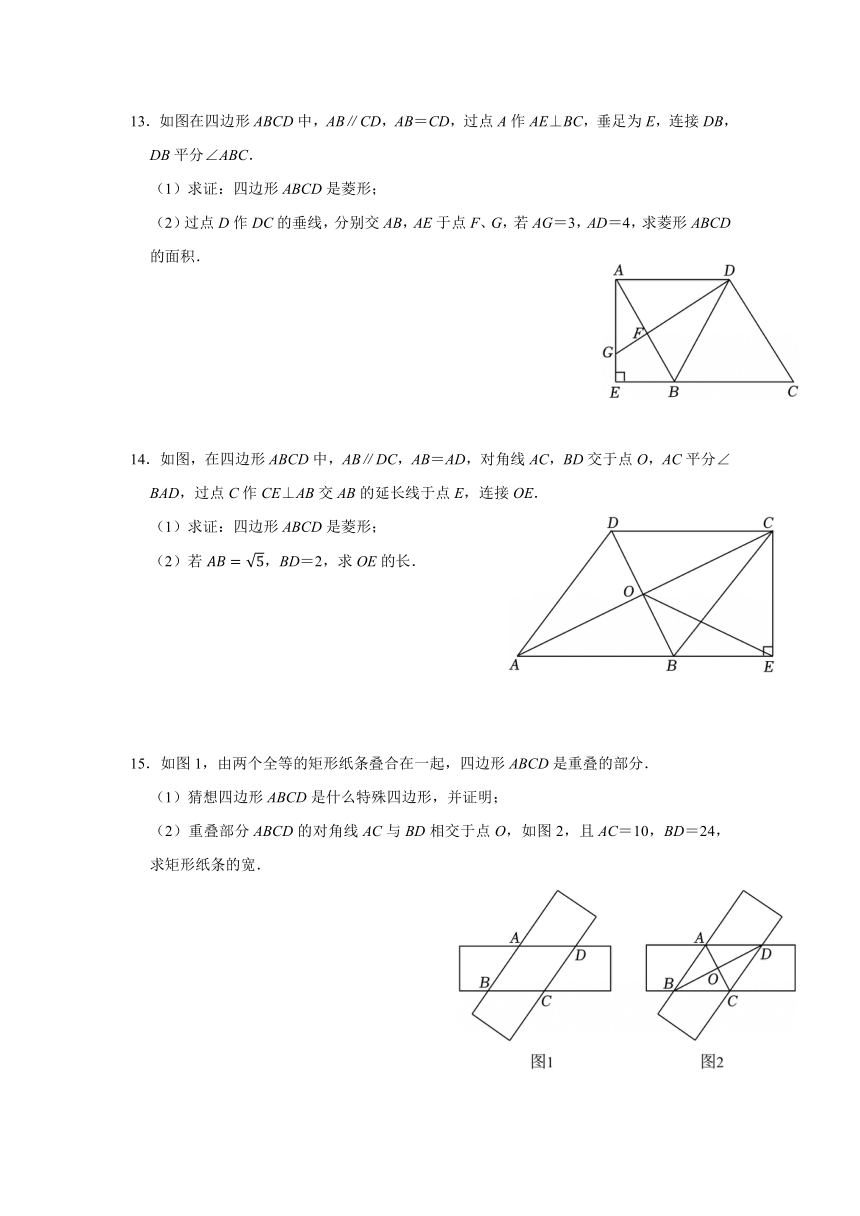
13.如图在四边形ABCD中,AB∥CD,AB=CD,过点A作AE⊥BC,垂足为E,连接DB,DB平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DC的垂线,分别交AB,AE于点F、G,若AG=3,AD=4,求菱形ABCD的面积.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求OE的长.
15.如图1,由两个全等的矩形纸条叠合在一起,四边形ABCD是重叠的部分.
(1)猜想四边形ABCD是什么特殊四边形,并证明;
(2)重叠部分ABCD的对角线AC与BD相交于点O,如图2,且AC=10,BD=24,求矩形纸条的宽.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C C D A C
二、填空题
6.【解答】解:设菱形的另一条对角线长为x,
由题意得,,
∴x=8,
即菱形的另一条对角线长为8,
∵菱形的对角线互相垂直平分,
∴菱形的边长,
故答案为:5.
7.【解答】解:若AC为边,CD是对角线,
∵ADBC为菱形,
∴AC=AD且A(﹣3,0),C(0,4),D(﹣6,z),
∴32+42=(﹣3+6)2+z 2,
z1=4,z2=﹣4(舍去),
若AC为对角线,
根据题意可求AC解析式yACx+4,
∵BD⊥AC,
∴设BD解析式yBDx+b且过AC中点(,2),
∴2()+b,
b,
∴BD解析式yBDx且过D(﹣6,z),
∴z,
故答案为:4或.
8.【解答】解:如图,连接AC交BD于O,连接AP,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC,BO=DO,∠ABO,
∴∠AOB=90°,
∴AOAB=2,
∴,
∵S△ABDS菱形ABCD=S△ABP+S△ADP,
∴4×EP4×PF,
∴PE+PF=2,
故答案为:2.
9.【解答】解:∵四边形ABCD是菱形,
∴OA=OC,OB=ODBD,BD⊥AC,
∴BD=16,
∵S菱形ABCDAC×BD=96,
∴AC=12,
∵CE⊥AD,
∴∠AEC=90°,
∴OEAC=6,
故答案为:6.
10.【解答】解:∵菱形ABCD是中心对称图形,且对角线BD与AC交于原点O,
∴点B与点D关于原点O对称,
∵B(6,m),D(n,4),
∴,
∴,
∴m﹣n=﹣4﹣(﹣6)=2,
故答案为:2.
三、解答题
11.【解答】(1)证明:∵CE⊥AE,
∴∠AEC=90°,
∵点F是AC中点,
∴,
∴∠FAE=∠FEA,
∵AC=2AB,
∴AB=AF=EF,
∵AD平分∠BAC,
∴∠BAE=∠FAE,
∴∠BAE=∠FEA,
∴BA∥EF,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形;
(2)解:作BH⊥AC交CA延长线于点H,则∠AHB=90°,
∵∠BAC=120°,
∴∠BAH=60°,
∴∠ABH=30°,
∴,
∵AC=2AB,
∴,
∴,
∴由勾股定理得:,
在Rt△BCH中,由勾股定理得:,
∴BC的长为14.
12.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点F在BC的延长线上,且CF=BC,
∴AD∥CF,AD=CF,
∴四边形ACFD是平行四边形,
∵CD∥AB,FA⊥AB交CD于点E,
∴∠CEF=∠ABF=90°,
∴FA⊥CD,
∴四边形ACFD是菱形.
(2)解:∵四边形ACFD是菱形,CD=AB=5,
∴DE=CECD,AE=FE,
∵∠DEF=90°,DF,
∴FE6,
∴FA=2FE=12,
∴S四边形ACFDFA CD12×5=30,
∴四边形ACFD的面积为30.
13.【解答】(1)证明:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,∠ABD=∠CDB,
∵DB平分∠ABC,
∴∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴CD=CB,
∴平行四边形ABCD是菱形;
(2)解:由(1)可知,四边形ABCD是菱形,
∴AB=AD=4,AD∥BC,
∵AE⊥BC,
∴AE⊥AD,
∴∠DAG=90°,
∴DG5,
∵AB∥CD,DG⊥DC,
∴DG⊥AB,
∴S△ADGDG AFAD AG,
∴AF,
∴DF,
∴S菱形ABCD=AB DF=4.
14.【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴,
在Rt△AOB中,,OB=1,
∴,
∴OE=OA=2.
15.【解答】解:(1)四边形ABCD是菱形,证明如下:
如图1,作AE⊥BC于E,AF⊥CD于F,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵由两个全等的矩形纸条叠合在一起,
∴两个矩形等宽,
∴AE=AF,
∵S四边形ABCD=AE×BC=AF×CD,
∴BC=CD,
∴四边形ABCD是菱形;
(2)设矩形纸条的宽为h,
∵四边形ABCD是菱形,AC=10,BD=24,
∴∠BOC=90°,,,
∴,
∵,
∴,
即矩形纸条的宽为.
一、选择题
1.在下列条件中选取一个作为增加条件,能使 ABCD成为菱形的是( )
A.AC=BD B.AB=DC C.AC⊥BD D.AD∥BC
2.依据所标数据,下列四边形不一定为菱形的是( )
A. B. C. D.
3.如图,菱形ABCD的对角线AC,BD相交于点O,E是边AB的中点,连接OE,若OE=3,则菱形ABCD的边长为( )
A.3 B.4 C.5 D.6
4.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
5.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥BC于点H,连接OH,∠BAD=56°,则∠DHO的度数是( )
A.38° B.34° C.28° D.24°
二、填空题
6.面积为24的菱形的一条对角线长为6,则这个菱形的边长为 .
7.在平面直角坐标系中,点A,B,C,D的坐标分别为(﹣3,0),(x,y),(0,4),(﹣6,z),若以点A,B,C,D为顶点的四边形是菱形,则z的值为 .
8.如图,在菱形ABCD中,∠ABC=60°,连接BD,点P是线段BD上一点,过点P作PE⊥AB,PF⊥AD,垂足分别为点E,F.若AB=4,则PE+PF的值为 .
9.如图,菱形ABCD的对角线AC、BD相交于点O,过点C作CE⊥AD于点E,连接OE,若OB=8,S菱形ABCD=96,则OE的长为 .
10.如图,菱形ABCD的对角线交于原点O,若点B的坐标为(6,m),点D的坐标为(n,4),则m﹣n的值为 .
三、解答题
11.如图,△ABC中,AC=2AB,AD平分∠BAC,过点C作CE⊥AD交AD延长线于点E,点F是AC中点,连接EF,EB.
(1)证明:四边形ABEF是菱形;
(2)若∠BAC=120°,,求边BC的长.
12.如图,在 ABCD中,FA⊥AB交CD于点E,交BC的延长线于点F,且CF=BC,连接AC,DF.
(1)求证:四边形ACFD是菱形;
(2)若AB=5,,求四边形ACFD的面积.
13.如图在四边形ABCD中,AB∥CD,AB=CD,过点A作AE⊥BC,垂足为E,连接DB,DB平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DC的垂线,分别交AB,AE于点F、G,若AG=3,AD=4,求菱形ABCD的面积.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求OE的长.
15.如图1,由两个全等的矩形纸条叠合在一起,四边形ABCD是重叠的部分.
(1)猜想四边形ABCD是什么特殊四边形,并证明;
(2)重叠部分ABCD的对角线AC与BD相交于点O,如图2,且AC=10,BD=24,求矩形纸条的宽.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C C D A C
二、填空题
6.【解答】解:设菱形的另一条对角线长为x,
由题意得,,
∴x=8,
即菱形的另一条对角线长为8,
∵菱形的对角线互相垂直平分,
∴菱形的边长,
故答案为:5.
7.【解答】解:若AC为边,CD是对角线,
∵ADBC为菱形,
∴AC=AD且A(﹣3,0),C(0,4),D(﹣6,z),
∴32+42=(﹣3+6)2+z 2,
z1=4,z2=﹣4(舍去),
若AC为对角线,
根据题意可求AC解析式yACx+4,
∵BD⊥AC,
∴设BD解析式yBDx+b且过AC中点(,2),
∴2()+b,
b,
∴BD解析式yBDx且过D(﹣6,z),
∴z,
故答案为:4或.
8.【解答】解:如图,连接AC交BD于O,连接AP,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC,BO=DO,∠ABO,
∴∠AOB=90°,
∴AOAB=2,
∴,
∵S△ABDS菱形ABCD=S△ABP+S△ADP,
∴4×EP4×PF,
∴PE+PF=2,
故答案为:2.
9.【解答】解:∵四边形ABCD是菱形,
∴OA=OC,OB=ODBD,BD⊥AC,
∴BD=16,
∵S菱形ABCDAC×BD=96,
∴AC=12,
∵CE⊥AD,
∴∠AEC=90°,
∴OEAC=6,
故答案为:6.
10.【解答】解:∵菱形ABCD是中心对称图形,且对角线BD与AC交于原点O,
∴点B与点D关于原点O对称,
∵B(6,m),D(n,4),
∴,
∴,
∴m﹣n=﹣4﹣(﹣6)=2,
故答案为:2.
三、解答题
11.【解答】(1)证明:∵CE⊥AE,
∴∠AEC=90°,
∵点F是AC中点,
∴,
∴∠FAE=∠FEA,
∵AC=2AB,
∴AB=AF=EF,
∵AD平分∠BAC,
∴∠BAE=∠FAE,
∴∠BAE=∠FEA,
∴BA∥EF,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形;
(2)解:作BH⊥AC交CA延长线于点H,则∠AHB=90°,
∵∠BAC=120°,
∴∠BAH=60°,
∴∠ABH=30°,
∴,
∵AC=2AB,
∴,
∴,
∴由勾股定理得:,
在Rt△BCH中,由勾股定理得:,
∴BC的长为14.
12.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点F在BC的延长线上,且CF=BC,
∴AD∥CF,AD=CF,
∴四边形ACFD是平行四边形,
∵CD∥AB,FA⊥AB交CD于点E,
∴∠CEF=∠ABF=90°,
∴FA⊥CD,
∴四边形ACFD是菱形.
(2)解:∵四边形ACFD是菱形,CD=AB=5,
∴DE=CECD,AE=FE,
∵∠DEF=90°,DF,
∴FE6,
∴FA=2FE=12,
∴S四边形ACFDFA CD12×5=30,
∴四边形ACFD的面积为30.
13.【解答】(1)证明:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,∠ABD=∠CDB,
∵DB平分∠ABC,
∴∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴CD=CB,
∴平行四边形ABCD是菱形;
(2)解:由(1)可知,四边形ABCD是菱形,
∴AB=AD=4,AD∥BC,
∵AE⊥BC,
∴AE⊥AD,
∴∠DAG=90°,
∴DG5,
∵AB∥CD,DG⊥DC,
∴DG⊥AB,
∴S△ADGDG AFAD AG,
∴AF,
∴DF,
∴S菱形ABCD=AB DF=4.
14.【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴,
在Rt△AOB中,,OB=1,
∴,
∴OE=OA=2.
15.【解答】解:(1)四边形ABCD是菱形,证明如下:
如图1,作AE⊥BC于E,AF⊥CD于F,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵由两个全等的矩形纸条叠合在一起,
∴两个矩形等宽,
∴AE=AF,
∵S四边形ABCD=AE×BC=AF×CD,
∴BC=CD,
∴四边形ABCD是菱形;
(2)设矩形纸条的宽为h,
∵四边形ABCD是菱形,AC=10,BD=24,
∴∠BOC=90°,,,
∴,
∵,
∴,
即矩形纸条的宽为.
