空间向量的数量积运算(第二课时)
文档属性
| 名称 | 空间向量的数量积运算(第二课时) |  | |
| 格式 | rar | ||
| 文件大小 | 260.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-06 07:39:00 | ||
图片预览



文档简介
课件10张PPT。3.1空间向量及其运算(4)
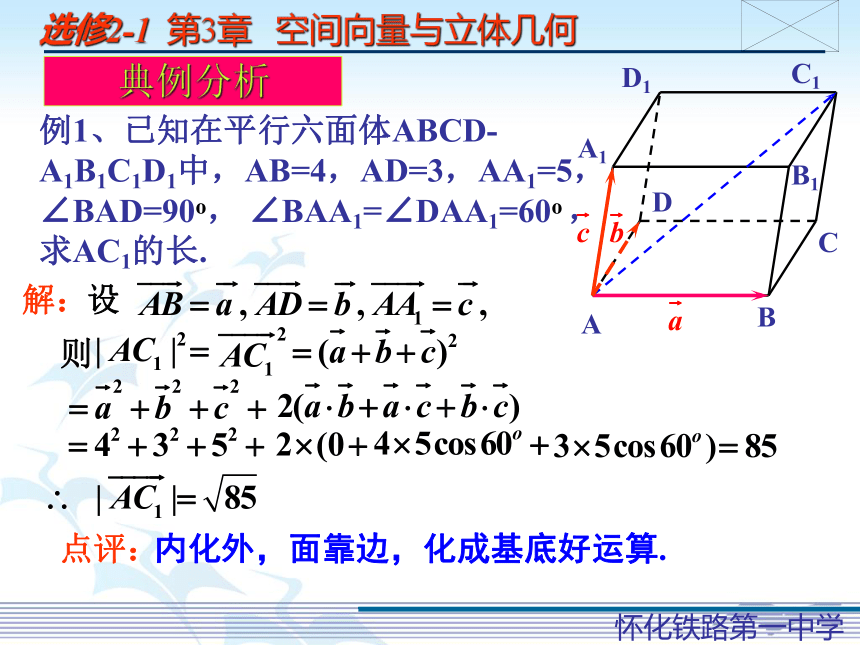
空间向量的数量积运算(二)1、数量积定义2、数量积常用性质:对两非零向量 有:3、数量积与实数积的不同之处:(1)数量积运算不满足 律; 乘法公式一般不成立;结合三次或三次以上的(2)数量积运算 约分.不可朝花夕拾典例分析例1、已知在平行六面体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=5,∠BAD=90o, ∠BAA1=∠DAA1=60o ,求AC1的长.A1B1C1D1ABCD设解:则点评:内化外,面靠边,化成基底好运算.例2、已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DE⊥α ,∠DBE=30o ,如果AB=a,AC=BD=b,求C、D间的距离.AB解:CDE设由AC⊥α知, AC⊥AB,α由∠DBE=30o知,则点评: 选择基底时,尽量选择已知长度、角度关系较多的三个向量.练习分析:1、把长AB和宽AD分别为 和2的长方形ABCD,
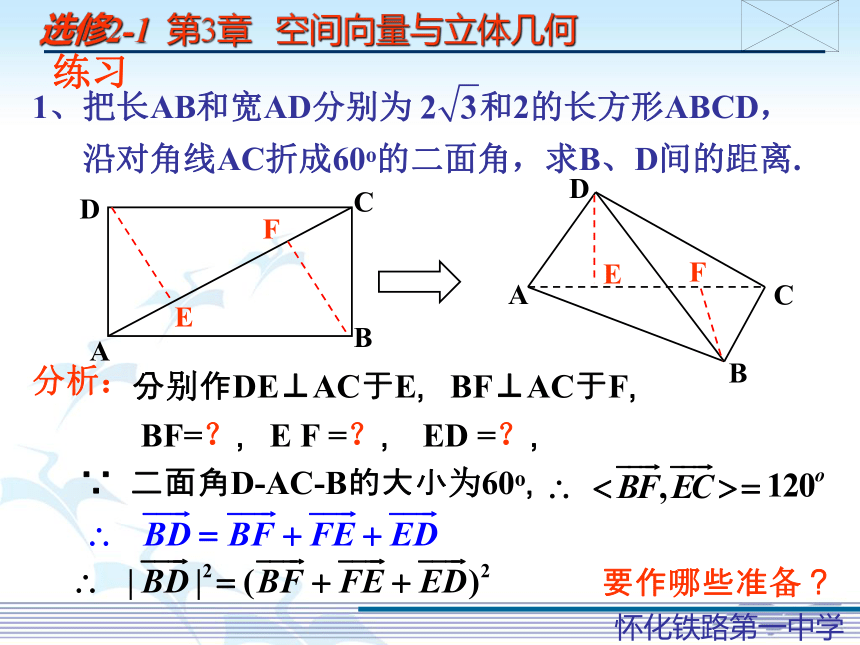
沿对角线AC折成60o的二面角,求B、D间的距离.分别作DE⊥AC于E,BF⊥AC于F,∵ 二面角D-AC-B的大小为60o,要作哪些准备?BF=?,E F =?, ED =?,例3:空间正四面体OABC中, D、E分别是AB, OC的中点,求OD, BE所成角的余弦值.OABCDE解:设正四面体棱长为1,则故 OD与BE所成角的余弦值为点评: 两向量的夹角不一定是两直线所成角,也可能是
其补角,注意正负的判断.45o练习2.如图, 在空间四边形ABCD中, OA=8, AB=6, AC=4, BC=5, ∠OAC=45°, ∠OAB=60°, 求OA与BC的夹角的余弦值. OABC864560o解:故OA与BC所成的角的余弦值为归纳总结解题时都应注意(1) 基本思路——(2) 基底的选择——内化外,面靠边,化成基底好运算.尽量选择已知长度、角度关系较多的三个向量此外,在利用向量求两条直线所成的角时注意对应两向量夹角的余弦两直线所成的角的余弦=| |再见!
空间向量的数量积运算(二)1、数量积定义2、数量积常用性质:对两非零向量 有:3、数量积与实数积的不同之处:(1)数量积运算不满足 律; 乘法公式一般不成立;结合三次或三次以上的(2)数量积运算 约分.不可朝花夕拾典例分析例1、已知在平行六面体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=5,∠BAD=90o, ∠BAA1=∠DAA1=60o ,求AC1的长.A1B1C1D1ABCD设解:则点评:内化外,面靠边,化成基底好运算.例2、已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DE⊥α ,∠DBE=30o ,如果AB=a,AC=BD=b,求C、D间的距离.AB解:CDE设由AC⊥α知, AC⊥AB,α由∠DBE=30o知,则点评: 选择基底时,尽量选择已知长度、角度关系较多的三个向量.练习分析:1、把长AB和宽AD分别为 和2的长方形ABCD,
沿对角线AC折成60o的二面角,求B、D间的距离.分别作DE⊥AC于E,BF⊥AC于F,∵ 二面角D-AC-B的大小为60o,要作哪些准备?BF=?,E F =?, ED =?,例3:空间正四面体OABC中, D、E分别是AB, OC的中点,求OD, BE所成角的余弦值.OABCDE解:设正四面体棱长为1,则故 OD与BE所成角的余弦值为点评: 两向量的夹角不一定是两直线所成角,也可能是
其补角,注意正负的判断.45o练习2.如图, 在空间四边形ABCD中, OA=8, AB=6, AC=4, BC=5, ∠OAC=45°, ∠OAB=60°, 求OA与BC的夹角的余弦值. OABC864560o解:故OA与BC所成的角的余弦值为归纳总结解题时都应注意(1) 基本思路——(2) 基底的选择——内化外,面靠边,化成基底好运算.尽量选择已知长度、角度关系较多的三个向量此外,在利用向量求两条直线所成的角时注意对应两向量夹角的余弦两直线所成的角的余弦=| |再见!
