1.2 任意角 课件(共21张PPT) 2024-2025学年北师大版高中数学必修第二册
文档属性
| 名称 | 1.2 任意角 课件(共21张PPT) 2024-2025学年北师大版高中数学必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
§ 2.1角的概念的推广
知识 目标
1.理解正角、负角和零角的概念.(数学抽象)
2.掌握象限角的特征及其表示方法.(数学抽象)
3.理解终边相同的角的概念,会表示终边相同的角的集合.(逻辑推理)
1.通过角的概念的学习,逐步培养数学抽象素养.
2.借助角的表示,培养逻辑推理素养.
数学素养
情景导入
问题1:初中对角的定义是什么呢?
(静态定义)具有公共顶点的两条射线组成的图形
问题3:角的范围是多少?
问题2:初中学习过的角有哪些?
(1)锐角:大于小于的角叫作锐角;
(2)直角:等于的角叫作直角;
(3)钝角:大于小于的角叫作顿角;
(4)平角:等于的角叫作平角;
(5)周角:等于的角叫作周角。
0°<α<360°
问题4:在现实生活中有没有不在 范围内的角?
比如跳水的“向前翻腾四周半抱膝3.5”、“过山车运动”、“跳水转体三周 ”等
思考:通过以上的例子说说角是怎么来的?
1任意角的概念
①定义:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
点O 叫做角α的顶点,
射线OA叫做角α的始边,
射线OB叫做角α的终边.
注意:旋转中心、旋转方向和旋转量
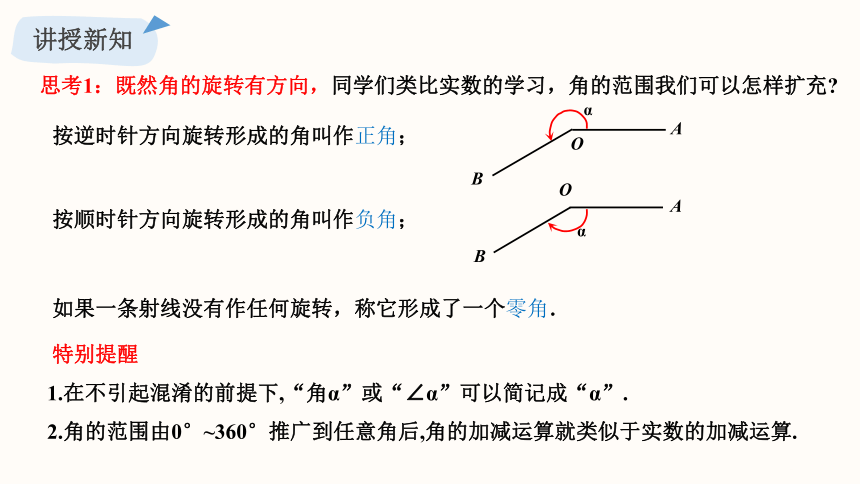
思考1:既然角的旋转有方向,同学们类比实数的学习,角的范围我们可以怎样扩充
1.在不引起混淆的前提下,“角α”或“∠α”可以简记成“α”.
2.角的范围由0°~360°推广到任意角后,角的加减运算就类似于实数的加减运算.
特别提醒
按逆时针方向旋转形成的角叫作正角;
按顺时针方向旋转形成的角叫作负角;
如果一条射线没有作任何旋转,称它形成了一个零角.
A
B
O
α
A
B
O
α
例1 思考下面角度应该如何表示:
(1)你的手表慢了5分钟,想将它校准,分针应该旋转多少度?
(2)假如你的手表快了1.5小时,想将它校准,分针应该旋转多少度?
(3)已知∠AOB=60°,将射线OB绕O点顺时针旋转30°到OC,则∠AOC=?如果是逆时针呢?
典例分析
-300
5400
300 900
1.将射线OM绕端点O按逆时针方向旋转120°所得的角为( )
A.120° B.-120°
C.60° D.240°
A
思考2:在同一坐标下中画出下列各角并观察图像,这些角有何特点?
与300终边相同的角的一般形式为300+ k · 360° ,k∈Z
写成集合形式就是S={ β| β= 300+ k· 360° ,k∈ Z}
思考: 将30°推广到一般角,结论α应该是什么?
-3300 300 3900
x
y
o
3900
-3300
300
角的终边相同
思考3:如何从任意角的运算方便对
你发现的规律进行解释?
2、终边相同的角
一般地,所有与α终边相同的角,连同角α在内,可构成一个集合
S={ β| β=α + k· 360° ,k∈ Z}
即任何一个与角α终边相同的角,都可以表示成角α与周角的整数倍的和。
注意:(1)“k∈Z”不能少;
(2)终边相同的角不一定相等,但相等的角终边一定相同;
(3)“k· -α360°”与“α”之间是“+”,“k· 360°-α”可以理解为“k· 360°+()”;
(4)终边相同的角的表达形式不唯一。如α=30°+k· 360°与β=-330°+k· 360°都表示终边与30°终边相同的角。
例2. 写出与下列各角终边相同的角的集合S,并把S中在-360 ~720 间的角写出来:
(1) 60 ;(2) -21 ;(3) 363 14′.
解:(1) S={β| β=k·360 +60 ,k∈Z },
S中在-360 ~720 间的角是
-1×360 +60 =-280 ;
0×360 +60 =60 ;
1×360 +60 =420 .
如何求与已知角α终边
相同的最小正角
(即0 ~360 )?
(2) S={β| β=k·360 -21 , k∈Z)}
S中在-360 ~720 间的角是
0×360 -21 =-21 ;
1×360 -21 =339 ;
2×360 -21 =699 .
(3) {β| β=k·360 + 3 14’ , k∈Z }
S中在-360 ~720 间的角是
-1×360 +3 14’=-356 46’;
0×360 +3 14’=3 14’;
1×360 +3 14’=363 14’.
3 象限角
终边落在第几象限就是第几象限角
注意:
1角的顶点与坐标原点重合,
2角的始边与x轴的非负半轴重合.
x
O
y
思考:如何表示各象限的角?
象限角
想一想:锐角是第几象限的角?
例3、判断下列各角是第几象限角
(1) (2) (3)
解(1)
所以与角与角终边相同,而是第三象限角,所以是第三象限角.
(2)第三象限角
(3)第二象限角
4 轴线角
如果角的终边落在坐标轴上,则该角不属于任何一个象限.
终边在坐标轴上的角:S={α|α=k·90°,k∈Z}
终边落在x轴上的角的集合S={α|α=k·180°,k∈Z},
终边落在y轴上的角的集合S={α|α=k·180°+90°,k∈Z}
例4 写出终边落在X轴上的角的集合。
解: 终边落在X轴正半轴上的角的集合为
S1={β| β=00+k 3600,k∈Z}
={β| β=00+2k 1800,k∈Z}
终边落在X轴负半轴上的角的集合为
S2={β| β=1800+k 3600,k∈Z}
={β| β=1800+2k 1800,k∈Z}
={β| β=(2k+1)1800 ,k∈Z}
所以终边落在x轴上的角的集合为
S=S1∪S2={β| β=k 1800 ,k∈Z}
想一想:终边落在y轴上的角的集合呢?
{β| β=900+k 1800 ,k∈Z}
终边落在坐标系的某个区间的角
1.用集合表示终边与45o相同的角
2.用集合表示终边落在阴影部分的角
思考: 将45°推广到一般角,结论α应该是什么?
y
x
O
始边
终边
5.区间角
1.判断正误(正确的打“√”,错误的打“×”).
(1)第一象限的角一定是正角.( )
(2)第二象限角是钝角.( )
(3)锐角都是第一象限角.( )
×
×
√
2.在下列说法中:①0°~90°的角是第一象限角;②第二象限角大于第一象限角;③钝角都是第二象限角;④小于90°的角都是锐角.其中错误说法的序号为________.
3.若角α的终边经过点M(0,-3),则角α( )
A.是第三象限角 B.是第四象限角
C.既是第三象限角又是第四象限角 D.不属于任何一个象限
①②④
D
4.写出终边落在图中阴影部分(包括边界)的角的集合.
解:终边落在OA位置上的角的集合为{α|α=90°+45°+k·360°,k∈Z}
={α|α=135°+k·360°,k∈Z},
终边落在OB位置上的角的集合为{β|β=-30°+k·360°,k∈Z}.
故阴影部分角的集合可表示为{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}.
§ 2.1角的概念的推广
知识 目标
1.理解正角、负角和零角的概念.(数学抽象)
2.掌握象限角的特征及其表示方法.(数学抽象)
3.理解终边相同的角的概念,会表示终边相同的角的集合.(逻辑推理)
1.通过角的概念的学习,逐步培养数学抽象素养.
2.借助角的表示,培养逻辑推理素养.
数学素养
情景导入
问题1:初中对角的定义是什么呢?
(静态定义)具有公共顶点的两条射线组成的图形
问题3:角的范围是多少?
问题2:初中学习过的角有哪些?
(1)锐角:大于小于的角叫作锐角;
(2)直角:等于的角叫作直角;
(3)钝角:大于小于的角叫作顿角;
(4)平角:等于的角叫作平角;
(5)周角:等于的角叫作周角。
0°<α<360°
问题4:在现实生活中有没有不在 范围内的角?
比如跳水的“向前翻腾四周半抱膝3.5”、“过山车运动”、“跳水转体三周 ”等
思考:通过以上的例子说说角是怎么来的?
1任意角的概念
①定义:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
点O 叫做角α的顶点,
射线OA叫做角α的始边,
射线OB叫做角α的终边.
注意:旋转中心、旋转方向和旋转量
思考1:既然角的旋转有方向,同学们类比实数的学习,角的范围我们可以怎样扩充
1.在不引起混淆的前提下,“角α”或“∠α”可以简记成“α”.
2.角的范围由0°~360°推广到任意角后,角的加减运算就类似于实数的加减运算.
特别提醒
按逆时针方向旋转形成的角叫作正角;
按顺时针方向旋转形成的角叫作负角;
如果一条射线没有作任何旋转,称它形成了一个零角.
A
B
O
α
A
B
O
α
例1 思考下面角度应该如何表示:
(1)你的手表慢了5分钟,想将它校准,分针应该旋转多少度?
(2)假如你的手表快了1.5小时,想将它校准,分针应该旋转多少度?
(3)已知∠AOB=60°,将射线OB绕O点顺时针旋转30°到OC,则∠AOC=?如果是逆时针呢?
典例分析
-300
5400
300 900
1.将射线OM绕端点O按逆时针方向旋转120°所得的角为( )
A.120° B.-120°
C.60° D.240°
A
思考2:在同一坐标下中画出下列各角并观察图像,这些角有何特点?
与300终边相同的角的一般形式为300+ k · 360° ,k∈Z
写成集合形式就是S={ β| β= 300+ k· 360° ,k∈ Z}
思考: 将30°推广到一般角,结论α应该是什么?
-3300 300 3900
x
y
o
3900
-3300
300
角的终边相同
思考3:如何从任意角的运算方便对
你发现的规律进行解释?
2、终边相同的角
一般地,所有与α终边相同的角,连同角α在内,可构成一个集合
S={ β| β=α + k· 360° ,k∈ Z}
即任何一个与角α终边相同的角,都可以表示成角α与周角的整数倍的和。
注意:(1)“k∈Z”不能少;
(2)终边相同的角不一定相等,但相等的角终边一定相同;
(3)“k· -α360°”与“α”之间是“+”,“k· 360°-α”可以理解为“k· 360°+()”;
(4)终边相同的角的表达形式不唯一。如α=30°+k· 360°与β=-330°+k· 360°都表示终边与30°终边相同的角。
例2. 写出与下列各角终边相同的角的集合S,并把S中在-360 ~720 间的角写出来:
(1) 60 ;(2) -21 ;(3) 363 14′.
解:(1) S={β| β=k·360 +60 ,k∈Z },
S中在-360 ~720 间的角是
-1×360 +60 =-280 ;
0×360 +60 =60 ;
1×360 +60 =420 .
如何求与已知角α终边
相同的最小正角
(即0 ~360 )?
(2) S={β| β=k·360 -21 , k∈Z)}
S中在-360 ~720 间的角是
0×360 -21 =-21 ;
1×360 -21 =339 ;
2×360 -21 =699 .
(3) {β| β=k·360 + 3 14’ , k∈Z }
S中在-360 ~720 间的角是
-1×360 +3 14’=-356 46’;
0×360 +3 14’=3 14’;
1×360 +3 14’=363 14’.
3 象限角
终边落在第几象限就是第几象限角
注意:
1角的顶点与坐标原点重合,
2角的始边与x轴的非负半轴重合.
x
O
y
思考:如何表示各象限的角?
象限角
想一想:锐角是第几象限的角?
例3、判断下列各角是第几象限角
(1) (2) (3)
解(1)
所以与角与角终边相同,而是第三象限角,所以是第三象限角.
(2)第三象限角
(3)第二象限角
4 轴线角
如果角的终边落在坐标轴上,则该角不属于任何一个象限.
终边在坐标轴上的角:S={α|α=k·90°,k∈Z}
终边落在x轴上的角的集合S={α|α=k·180°,k∈Z},
终边落在y轴上的角的集合S={α|α=k·180°+90°,k∈Z}
例4 写出终边落在X轴上的角的集合。
解: 终边落在X轴正半轴上的角的集合为
S1={β| β=00+k 3600,k∈Z}
={β| β=00+2k 1800,k∈Z}
终边落在X轴负半轴上的角的集合为
S2={β| β=1800+k 3600,k∈Z}
={β| β=1800+2k 1800,k∈Z}
={β| β=(2k+1)1800 ,k∈Z}
所以终边落在x轴上的角的集合为
S=S1∪S2={β| β=k 1800 ,k∈Z}
想一想:终边落在y轴上的角的集合呢?
{β| β=900+k 1800 ,k∈Z}
终边落在坐标系的某个区间的角
1.用集合表示终边与45o相同的角
2.用集合表示终边落在阴影部分的角
思考: 将45°推广到一般角,结论α应该是什么?
y
x
O
始边
终边
5.区间角
1.判断正误(正确的打“√”,错误的打“×”).
(1)第一象限的角一定是正角.( )
(2)第二象限角是钝角.( )
(3)锐角都是第一象限角.( )
×
×
√
2.在下列说法中:①0°~90°的角是第一象限角;②第二象限角大于第一象限角;③钝角都是第二象限角;④小于90°的角都是锐角.其中错误说法的序号为________.
3.若角α的终边经过点M(0,-3),则角α( )
A.是第三象限角 B.是第四象限角
C.既是第三象限角又是第四象限角 D.不属于任何一个象限
①②④
D
4.写出终边落在图中阴影部分(包括边界)的角的集合.
解:终边落在OA位置上的角的集合为{α|α=90°+45°+k·360°,k∈Z}
={α|α=135°+k·360°,k∈Z},
终边落在OB位置上的角的集合为{β|β=-30°+k·360°,k∈Z}.
故阴影部分角的集合可表示为{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
