20.2 数据的波动程度培优练习(含答案)
文档属性
| 名称 | 20.2 数据的波动程度培优练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 226.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 00:00:00 | ||
图片预览



文档简介
20.2数据的波动程度培优练习人教版2024—2025学年八年级下册
一、选择题
1.某校足球队队员年龄的平均数为13岁,方差为2岁2,若两年后该足球队队员不变,则下列关于队员前后年龄的说法,正确的是( )
A.平均数不变,方差改变
B.平均数不变,方差不变
C.平均数改变,方差不变
D.平均数改变,方差改变
2.扬州某日天气预报显示最高气温为5℃,最低气温为﹣4℃,则该日的气温极差为( )
A.1℃ B.6℃ C.9℃ D.10℃
3.选拔一名选手参加区中学生男子百米比赛,我校四名中学生参加了训练,他们成绩的平均数及其方差s2如表所示:
甲 乙 丙 丁
12″33 10″26 10″26 11″29
S2 1.1 1.1 1.3 1.6
要选拔一名成绩好且发挥稳定的同学,最合适的是( )
A.甲 B.乙 C.丙 D.丁
4.小明根据方差公式,分析和计算得出了四个结论,其中不正确的是( )
A.x1=1 B.中位数是3 C.n=5 D.s2=2.4
5.如图,甲、乙两支仪仗队员的平均身高相同时,设两支队员身高数据的方差为、S乙2,则下列关系正确的是( )
A. B.
C. D.无法确定
二、填空题
6.若一组数据“4,a,5,6,b”的平均数是5,众数是5,则这组数据的方差为 .
7.甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.6m,方差分别为0.2,0.08,成绩比较稳定的是 (填“甲”或“乙”).
8.在学校数学课外活动竞赛中,某班5名学生参赛成绩分别为:81,83,85,88,88,则这5名学生的参赛成绩的极差是 .
9.甲、乙两地1月份连续五天的日平均气温如下表(单位:℃).
第1天 第2天 第3天 第4天 第5天
甲地气温 12 11 12 10 12
乙地气温 ﹣2 0 4 0 ﹣2
则甲、乙两地这5天日平均气温的方差大小关系为:S甲2 S乙2.(用“>”“<”或“=”填空)
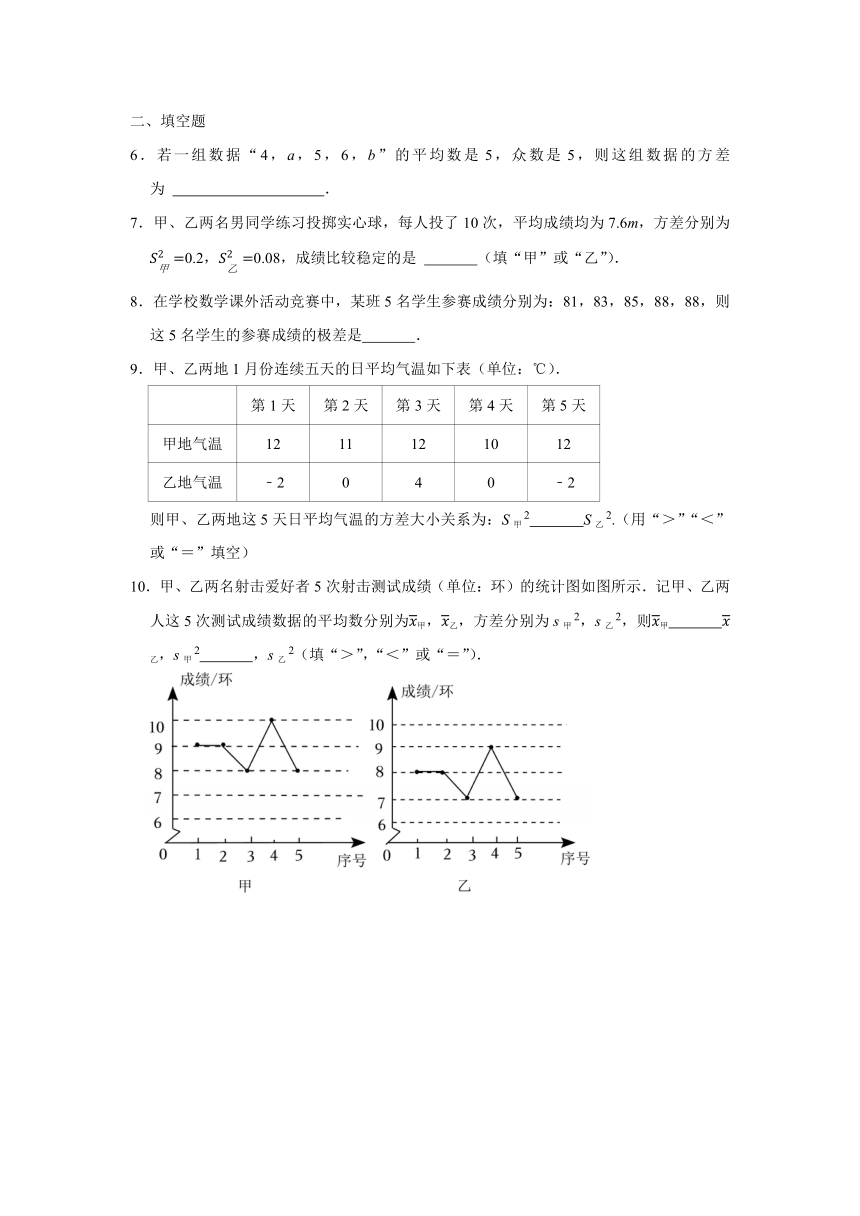
10.甲、乙两名射击爱好者5次射击测试成绩(单位:环)的统计图如图所示.记甲、乙两人这5次测试成绩数据的平均数分别为甲,乙,方差分别为s甲2,s乙2,则甲 乙,s甲2 ,s乙2(填“>”,“<”或“=”).
三、解答题
11.临近期末,为测试同学们的体育成绩情况,某校从九年级同学中任意选取40人,随机分成甲、乙两个小组进行“排球传垫球”测试(满分为15分).根据测试成绩绘制出下面的统计表和统计图.已知甲组的平均成绩为13.7分,方差为0.81.甲组成绩统计表:
成绩 12 13 14 15
人数 1 9 5 5
请根据上面的信息,解答下列问题:
(1)m= ,甲组成绩的中位数是 ,乙组成绩的众数是 ;
(2)判断哪个小组的成绩更加稳定?说明理由.
12.学校组织七、八年级学生参加了“国家安全知识”测试.已知七、八年级各有200人,现从两个年级分别随机抽取10名学生的测试成绩(单位:分)进行统计:
七年级:86,94,79,84,71,90,76,83,90,87.
八年级:88,76,90,78,87,93,75,87,87,79.
整理如下:
年级 平均数 中位数 众数 方差
七年级 84 a 90 44.4
八年级 84 87 b 36.6
根据以上信息,回答下列问题:
(1)填空:a= ,b= ;
A同学说:“这次测试我得了86分,位于年级中等偏上水平”,由此可判断他是 年级的学生;
(2)你认为哪个年级的学生掌握国家安全知识的总体水平较好?请给出一条理由.
13.某校举行了“珍爱生命,预防溺水”主题知识竞赛活动,八(1)、八(2)班各选取五名选手参赛.两班参赛选手成绩依次如下:(单位:分)
八(1)班:8,8,7,8,9
八(2)班:5,9,7,10,9
学校根据两班的成绩绘制了如下不完整的统计表:
班级 平均数 众数 中位数
八(1) 8 b c
八(2) a 9 9
根据以上信息,请解答下面的问题:
(1)填空:a= ,b= ,c= .
(2)已知八(1)班比赛成绩的方差是0.4,请你计算八(2)班比赛成绩的方差,并从方差的角度分析哪个班级成绩更稳定.
14.校园配餐备受关注,为让广大学生吃到安全放心的配餐,质量监督部门针对甲、乙两家配餐公司制作的同一种套餐的品质(卫生、口味等)进行了抽样调查,对套餐的品质进行评分(十分制).相同条件下,随机抽取了两家公司的套餐各10份样品,得分如下(单位:分):
甲组:5,6,6,6,6,6,7,9,9,10;
乙组:5,6,6,6,7,7,7,7,8,9.
组别 平均数 中位数 众数 方差
甲组 7 a 6 2.6
乙组 b 7 c 1.16
(1)上述表格中a= ,c= ;
(2)求b的值;
(3)若要从甲、乙两家配餐公司中选择一个公司为阳光中学配餐,你推荐哪家公司?请说明理由.
15.甘肃省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次 第六次
甲 10 8 9 8 10 9
乙 10 10 10 9 8
(1)求甲的平均成绩的环数;
(2)已知乙的平均成绩是9环,试计算其第二次测试成绩的环数;
(3)分别计算甲、乙六次测试成绩的方差,你认为推荐谁参加全国比赛更合适,请说明理由.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C C B D A
二、填空题
6.【解答】解:∵众数为5,
∴a,b中至少有一个是5,
∵平均数为5,
∴,
∴a+b=10,
∴a,b都是5,
∴这组数据的方差为;
故答案为:.
7.【解答】解:∵甲、乙两名男同学平均成绩均为7.6m,方差分别为0.2,0.08,
∴S甲2>S乙2,
∴乙同学的成绩比较稳定.
故答案为:乙.
8.【解答】解:本组数据中,最大数据是88,最小数据是81,
则极差为:88﹣81=7,
故答案为:7.
9.【解答】解:甲地的平均气温:(12+11+12+10+12)=11.4(℃),
乙地的平均气温:(﹣2+0+4+0﹣2)=0(℃),
∵甲地的方差是:[3×(12﹣11.4)2+(11﹣11.4)2+(10﹣11.4)2]=0.64,
乙地的方差是:[2×(﹣2﹣0)2+2×(0﹣0)2+(4﹣0)2]=4.8,
∴SS.
故答案为:<.
10.【解答】解:(9+9+8+10+8)=8.8.
(8+8+7+9+7)=7.8.
∵8.8>7.8.
∴.
S2甲[(9﹣8.8)2+(9﹣8.8)2+(8﹣8.8)2+(10﹣8.8)2+(8﹣8.8)2]=0.56.
S2乙[(8﹣7.8)2+(8﹣7.8)2+(7﹣7.8)2+(9﹣7.8)2+(7﹣7.8)2]=0.56.
∴S2甲=S2乙.
故答案为:>;=.
三、解答题
11.【解答】解:(1)m=20﹣2﹣9﹣6=3,
把甲组成绩从小到大排列,中位数是第10、11个数的平均数,
则中位教是13.5,
乙组成绩13分的最多,出现了9次,
则乙组成绩的众数是13;
故答案为:3,13.5,13;
(2)乙组的平均数是(分),
乙组的方差是:,
∴,
∴乙组的成绩更加稳定.
12.【解答】解:(1)把七年级10名学生的测试成绩排好顺序为:71,76,79,83,84,86,87,90,90,94,
根据中位数的定义可知,该组数据的中位数为a85,
八年级10名学生的成绩中87分的最多,有3人,所以众数b=87,
A同学得了86分,大于85分,位于年级中等偏上水平,由此可判断他是七年级的学生;
故答案为:85,87,七;
(2)我认为八年级的学生掌握国家安全知识的总体水平较好,
理由:因为七、八年级测试成绩的平均数相等,八年级测试成绩的方差小于七年级测试成绩的方差,所以八年级的学生掌握国家安全知识的总体水平较好.
13.【解答】(1)解:,
八(1)班:7,8,8,8,9,
∵8出现的次数最多,
∴众数为:8,
即b=8,c=(8+8)÷2=8,
故答案为:8,8,8;
(2)解:由(1)可知,八(2)班的平均数是8,
∴方差为:
=3.2,
∵3.2>0.4,
∴八(1)班成绩更稳定.
14.【解答】解:(1)甲组中第5个和第6个数据分别是6和6,所以a6,
乙组中7出现次数最多,所以c=7,
故答案为:6,7;
(2)乙组平均数b(5+6×3+7×4+8+9)=6.8;
(3)推荐乙公司(答案不唯一),理由如下:
虽然乙组的平均数小,但是乙组的平均数、众数和中位数都大于甲组,而且乙组的方差小,套餐质量稳定.
15.【解答】解:(1)(环).
答:甲的平均成绩是9环.
(2)9×6﹣10﹣10﹣10﹣9﹣8=7(环).
答:乙第二次测试成绩为7环.
(3),
,
,甲的成绩较稳定,
因此推荐甲参加全国比赛更合适.
一、选择题
1.某校足球队队员年龄的平均数为13岁,方差为2岁2,若两年后该足球队队员不变,则下列关于队员前后年龄的说法,正确的是( )
A.平均数不变,方差改变
B.平均数不变,方差不变
C.平均数改变,方差不变
D.平均数改变,方差改变
2.扬州某日天气预报显示最高气温为5℃,最低气温为﹣4℃,则该日的气温极差为( )
A.1℃ B.6℃ C.9℃ D.10℃
3.选拔一名选手参加区中学生男子百米比赛,我校四名中学生参加了训练,他们成绩的平均数及其方差s2如表所示:
甲 乙 丙 丁
12″33 10″26 10″26 11″29
S2 1.1 1.1 1.3 1.6
要选拔一名成绩好且发挥稳定的同学,最合适的是( )
A.甲 B.乙 C.丙 D.丁
4.小明根据方差公式,分析和计算得出了四个结论,其中不正确的是( )
A.x1=1 B.中位数是3 C.n=5 D.s2=2.4
5.如图,甲、乙两支仪仗队员的平均身高相同时,设两支队员身高数据的方差为、S乙2,则下列关系正确的是( )
A. B.
C. D.无法确定
二、填空题
6.若一组数据“4,a,5,6,b”的平均数是5,众数是5,则这组数据的方差为 .
7.甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.6m,方差分别为0.2,0.08,成绩比较稳定的是 (填“甲”或“乙”).
8.在学校数学课外活动竞赛中,某班5名学生参赛成绩分别为:81,83,85,88,88,则这5名学生的参赛成绩的极差是 .
9.甲、乙两地1月份连续五天的日平均气温如下表(单位:℃).
第1天 第2天 第3天 第4天 第5天
甲地气温 12 11 12 10 12
乙地气温 ﹣2 0 4 0 ﹣2
则甲、乙两地这5天日平均气温的方差大小关系为:S甲2 S乙2.(用“>”“<”或“=”填空)
10.甲、乙两名射击爱好者5次射击测试成绩(单位:环)的统计图如图所示.记甲、乙两人这5次测试成绩数据的平均数分别为甲,乙,方差分别为s甲2,s乙2,则甲 乙,s甲2 ,s乙2(填“>”,“<”或“=”).
三、解答题
11.临近期末,为测试同学们的体育成绩情况,某校从九年级同学中任意选取40人,随机分成甲、乙两个小组进行“排球传垫球”测试(满分为15分).根据测试成绩绘制出下面的统计表和统计图.已知甲组的平均成绩为13.7分,方差为0.81.甲组成绩统计表:
成绩 12 13 14 15
人数 1 9 5 5
请根据上面的信息,解答下列问题:
(1)m= ,甲组成绩的中位数是 ,乙组成绩的众数是 ;
(2)判断哪个小组的成绩更加稳定?说明理由.
12.学校组织七、八年级学生参加了“国家安全知识”测试.已知七、八年级各有200人,现从两个年级分别随机抽取10名学生的测试成绩(单位:分)进行统计:
七年级:86,94,79,84,71,90,76,83,90,87.
八年级:88,76,90,78,87,93,75,87,87,79.
整理如下:
年级 平均数 中位数 众数 方差
七年级 84 a 90 44.4
八年级 84 87 b 36.6
根据以上信息,回答下列问题:
(1)填空:a= ,b= ;
A同学说:“这次测试我得了86分,位于年级中等偏上水平”,由此可判断他是 年级的学生;
(2)你认为哪个年级的学生掌握国家安全知识的总体水平较好?请给出一条理由.
13.某校举行了“珍爱生命,预防溺水”主题知识竞赛活动,八(1)、八(2)班各选取五名选手参赛.两班参赛选手成绩依次如下:(单位:分)
八(1)班:8,8,7,8,9
八(2)班:5,9,7,10,9
学校根据两班的成绩绘制了如下不完整的统计表:
班级 平均数 众数 中位数
八(1) 8 b c
八(2) a 9 9
根据以上信息,请解答下面的问题:
(1)填空:a= ,b= ,c= .
(2)已知八(1)班比赛成绩的方差是0.4,请你计算八(2)班比赛成绩的方差,并从方差的角度分析哪个班级成绩更稳定.
14.校园配餐备受关注,为让广大学生吃到安全放心的配餐,质量监督部门针对甲、乙两家配餐公司制作的同一种套餐的品质(卫生、口味等)进行了抽样调查,对套餐的品质进行评分(十分制).相同条件下,随机抽取了两家公司的套餐各10份样品,得分如下(单位:分):
甲组:5,6,6,6,6,6,7,9,9,10;
乙组:5,6,6,6,7,7,7,7,8,9.
组别 平均数 中位数 众数 方差
甲组 7 a 6 2.6
乙组 b 7 c 1.16
(1)上述表格中a= ,c= ;
(2)求b的值;
(3)若要从甲、乙两家配餐公司中选择一个公司为阳光中学配餐,你推荐哪家公司?请说明理由.
15.甘肃省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次 第六次
甲 10 8 9 8 10 9
乙 10 10 10 9 8
(1)求甲的平均成绩的环数;
(2)已知乙的平均成绩是9环,试计算其第二次测试成绩的环数;
(3)分别计算甲、乙六次测试成绩的方差,你认为推荐谁参加全国比赛更合适,请说明理由.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C C B D A
二、填空题
6.【解答】解:∵众数为5,
∴a,b中至少有一个是5,
∵平均数为5,
∴,
∴a+b=10,
∴a,b都是5,
∴这组数据的方差为;
故答案为:.
7.【解答】解:∵甲、乙两名男同学平均成绩均为7.6m,方差分别为0.2,0.08,
∴S甲2>S乙2,
∴乙同学的成绩比较稳定.
故答案为:乙.
8.【解答】解:本组数据中,最大数据是88,最小数据是81,
则极差为:88﹣81=7,
故答案为:7.
9.【解答】解:甲地的平均气温:(12+11+12+10+12)=11.4(℃),
乙地的平均气温:(﹣2+0+4+0﹣2)=0(℃),
∵甲地的方差是:[3×(12﹣11.4)2+(11﹣11.4)2+(10﹣11.4)2]=0.64,
乙地的方差是:[2×(﹣2﹣0)2+2×(0﹣0)2+(4﹣0)2]=4.8,
∴SS.
故答案为:<.
10.【解答】解:(9+9+8+10+8)=8.8.
(8+8+7+9+7)=7.8.
∵8.8>7.8.
∴.
S2甲[(9﹣8.8)2+(9﹣8.8)2+(8﹣8.8)2+(10﹣8.8)2+(8﹣8.8)2]=0.56.
S2乙[(8﹣7.8)2+(8﹣7.8)2+(7﹣7.8)2+(9﹣7.8)2+(7﹣7.8)2]=0.56.
∴S2甲=S2乙.
故答案为:>;=.
三、解答题
11.【解答】解:(1)m=20﹣2﹣9﹣6=3,
把甲组成绩从小到大排列,中位数是第10、11个数的平均数,
则中位教是13.5,
乙组成绩13分的最多,出现了9次,
则乙组成绩的众数是13;
故答案为:3,13.5,13;
(2)乙组的平均数是(分),
乙组的方差是:,
∴,
∴乙组的成绩更加稳定.
12.【解答】解:(1)把七年级10名学生的测试成绩排好顺序为:71,76,79,83,84,86,87,90,90,94,
根据中位数的定义可知,该组数据的中位数为a85,
八年级10名学生的成绩中87分的最多,有3人,所以众数b=87,
A同学得了86分,大于85分,位于年级中等偏上水平,由此可判断他是七年级的学生;
故答案为:85,87,七;
(2)我认为八年级的学生掌握国家安全知识的总体水平较好,
理由:因为七、八年级测试成绩的平均数相等,八年级测试成绩的方差小于七年级测试成绩的方差,所以八年级的学生掌握国家安全知识的总体水平较好.
13.【解答】(1)解:,
八(1)班:7,8,8,8,9,
∵8出现的次数最多,
∴众数为:8,
即b=8,c=(8+8)÷2=8,
故答案为:8,8,8;
(2)解:由(1)可知,八(2)班的平均数是8,
∴方差为:
=3.2,
∵3.2>0.4,
∴八(1)班成绩更稳定.
14.【解答】解:(1)甲组中第5个和第6个数据分别是6和6,所以a6,
乙组中7出现次数最多,所以c=7,
故答案为:6,7;
(2)乙组平均数b(5+6×3+7×4+8+9)=6.8;
(3)推荐乙公司(答案不唯一),理由如下:
虽然乙组的平均数小,但是乙组的平均数、众数和中位数都大于甲组,而且乙组的方差小,套餐质量稳定.
15.【解答】解:(1)(环).
答:甲的平均成绩是9环.
(2)9×6﹣10﹣10﹣10﹣9﹣8=7(环).
答:乙第二次测试成绩为7环.
(3),
,
,甲的成绩较稳定,
因此推荐甲参加全国比赛更合适.
