2025年九年级数学中考三轮冲刺练习三角形压轴题综合训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺练习三角形压轴题综合训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 10:44:14 | ||
图片预览



文档简介
2025年九年级数学中考三轮冲刺练习三角形压轴题综合训练
一、选择题
1.如图,在正方形ABCD的边CD上有一点E,连接AE,把AE绕点E逆时针旋转90°,得到FE,连接CF并延长与AB的延长线交于点G.则的值为( )
A. B. C. D.
2.如图,在△ABC中,D是AC的中点,CE⊥AB,BD与CE交于点O,且BE=CD.下列说法错误的是( )
A.BD的垂直平分线一定与AB相交于点E
B.∠BDC=3∠ABD
C.当E为AB中点时,△ABC是等边三角形
D.当E为AB中点时,
3.如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,E分别在AC,BC边上运动,连结AE,BD交于点F,且始终满足ADCE,则下列结论:①;②∠DFE=135°;③△ABF面积的最大值是44;④CF的最小值是22.其中正确的是( )
A.①③ B.①②④ C.②③④ D.①②③④
4.如图,在菱形ABCD中,∠ABC=60°,AB=1,点P是BC边上一个动点,在BC延长线上找一点Q,使得点P和点Q关于点C对称,连结DP、AQ交于点M.当点P从B点运动到C点时,点M的运动路径长为( )
A. B. C. D.
5.我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则sinθ=( )
A. B. C. D.
二、填空题
6.如图,在△ABC中,AE1,BE1分别是内角∠CAB,外角∠CBD的三等分线,且∠E1AD∠CAB,∠E1BD∠CBD,在△ABE1中,AE2,BE2分别是内角∠E1AB,外角∠E1BD的三等分线,且∠E2AD∠E1AB,∠E2BD∠E1BD,…,以此规律作下去,若∠C=m°,则∠En= 度.
7.如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 ;(2)DG的长是 .
8.如图,四边形ABCD的两条对角线AC,BD互相垂直,AC=4,BD=6,则AD+BC的最小值是 .
9.如图,DE平分等边△ABC的面积,折叠△BDE得到△FDE,AC分别与DF,EF相交于G,H两点.若DG=m,EH=n,用含m,n的式子表示GH的长是 .
10.如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a,DF=b,连接AE,BE,若△ADE与△BEH的面积相等,则 .
三、解答题
11.综合与实践
如图1,在△ABC中,BD是∠ABC的平分线,BD的延长线交外角∠CAM的平分线于点E.
【发现结论】
结论1:∠AEB= ∠ACB;
结论2:当图1中∠ACB=90°时,如图2所示,延长BC交AE于点F,过点E作AF的垂线交BF于点G,交AC的延长线于点H.则AE与EG的数量关系是 .
【应用结论】
(1)求证:AH=GF;
(2)在图2中连接FH,AG,延长AG交FH于点N,补全图形,求证:.
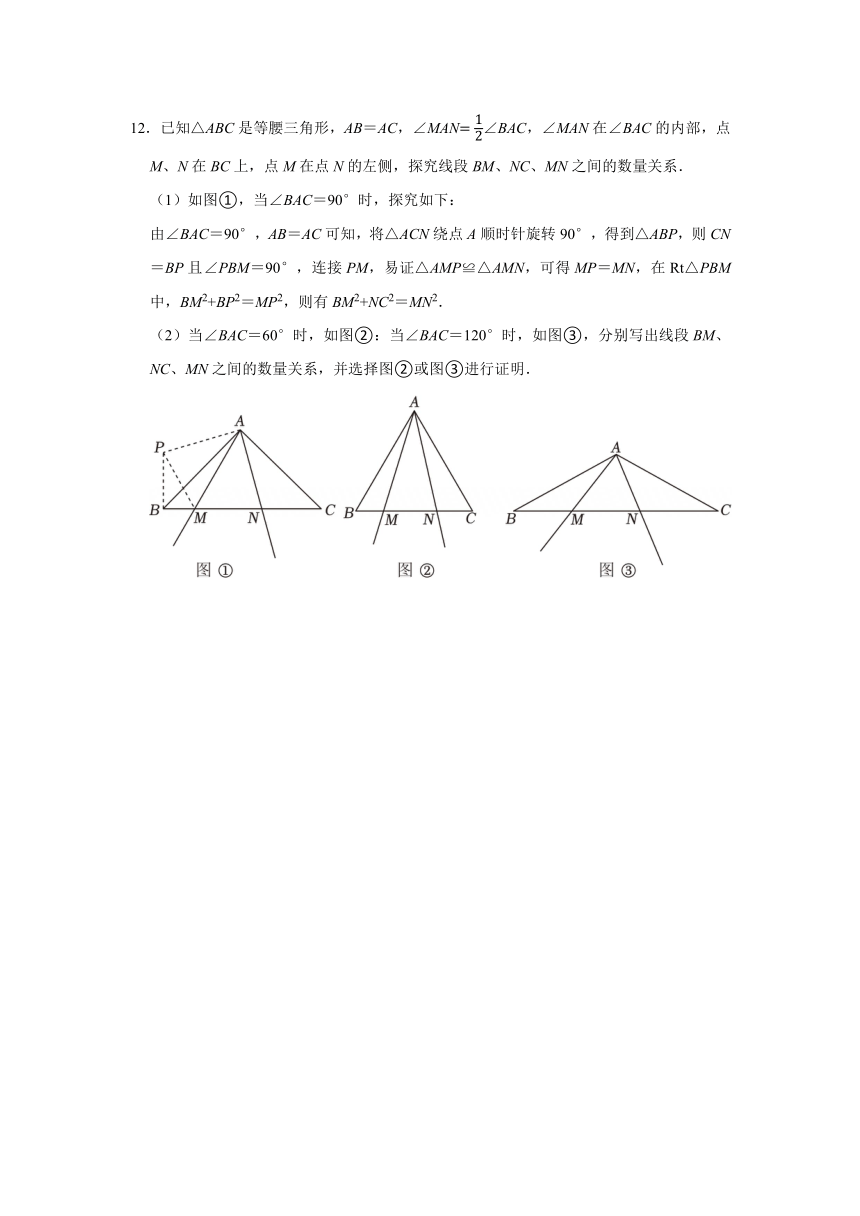
12.已知△ABC是等腰三角形,AB=AC,∠MAN∠BAC,∠MAN在∠BAC的内部,点M、N在BC上,点M在点N的左侧,探究线段BM、NC、MN之间的数量关系.
(1)如图①,当∠BAC=90°时,探究如下:
由∠BAC=90°,AB=AC可知,将△ACN绕点A顺时针旋转90°,得到△ABP,则CN=BP且∠PBM=90°,连接PM,易证△AMP≌△AMN,可得MP=MN,在Rt△PBM中,BM2+BP2=MP2,则有BM2+NC2=MN2.
(2)当∠BAC=60°时,如图②:当∠BAC=120°时,如图③,分别写出线段BM、NC、MN之间的数量关系,并选择图②或图③进行证明.
13.探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
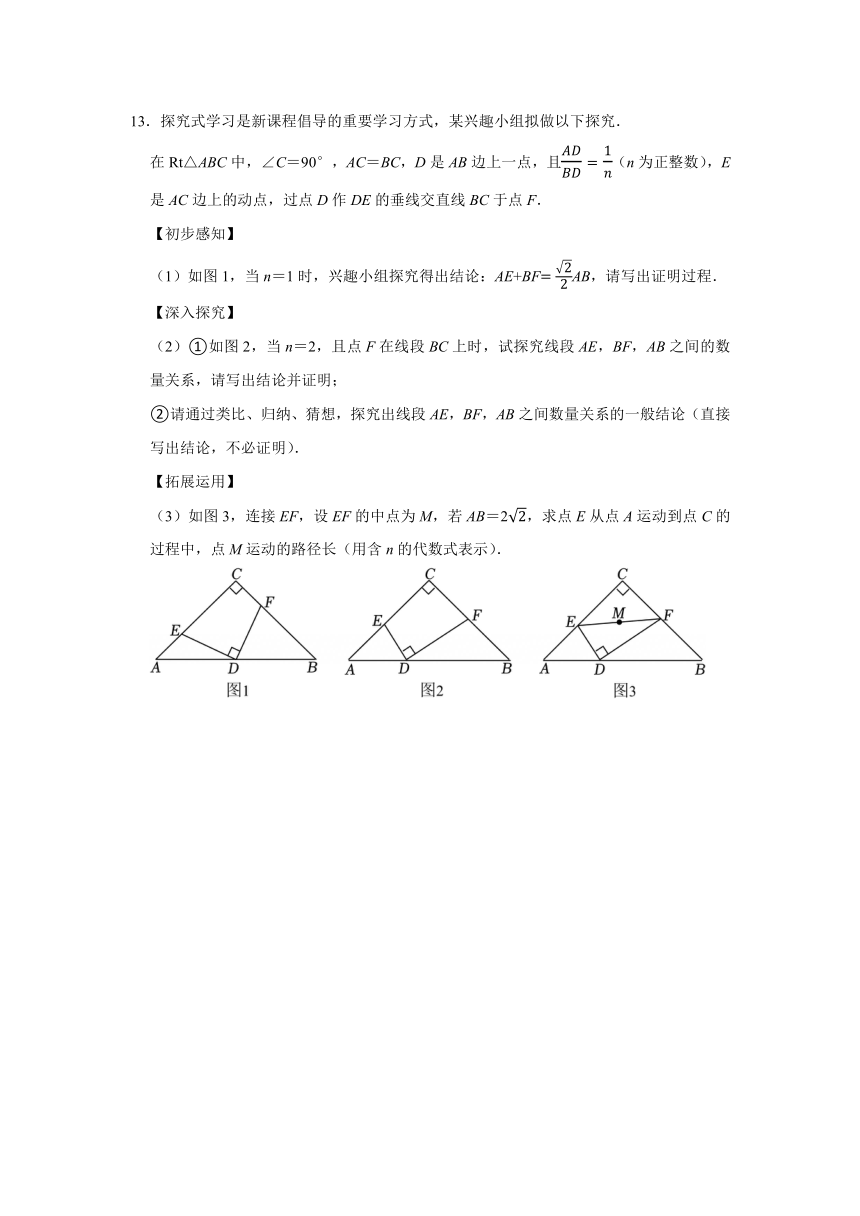
在Rt△ABC中,∠C=90°,AC=BC,D是AB边上一点,且(n为正整数),E是AC边上的动点,过点D作DE的垂线交直线BC于点F.
【初步感知】
(1)如图1,当n=1时,兴趣小组探究得出结论:AE+BFAB,请写出证明过程.
【深入探究】
(2)①如图2,当n=2,且点F在线段BC上时,试探究线段AE,BF,AB之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段AE,BF,AB之间数量关系的一般结论(直接写出结论,不必证明).
【拓展运用】
(3)如图3,连接EF,设EF的中点为M,若AB=2,求点E从点A运动到点C的过程中,点M运动的路径长(用含n的代数式表示).
14.如图,在等边三角形ABC中,点M为AB边上任意一点,延长BC至点N,使CN=AM,连接MN交AC于点P,MH⊥AC于点H.
(1)求证:MP=NP;
(2)若AB=a,求线段PH的长(结果用含a的代数式表示).
15.如图,已知矩形ABCD中,AB=8,BC=x(0<x<8),将△ACB沿AC对折到△ACE的位置,AE和CD交于点F.
(1)求证:△CEF≌△ADF;
(2)求tan∠DAF的值(用含x的式子表示).
参考答案
一、选择题
题号 1 2 3 4 5
答案 A D D B A
二、填空题
6.答案为:.
7. 30° ;.
8.答案为:.
9.答案为:.
10.答案为:3.
三、解答题
11.【解答】【发现结论】解:结论1:∵BD是∠ABC的平分线,
∴∠ABC=2∠ABE,
∵AE是∠CAM的平分线,
∴∠CAM=2∠EAM,
∵∠CAM=∠ACB+∠ABC,
∴2∠EAM=∠ACB+2∠ABE,
∵∠EAM=∠AEB+∠ABE,
∴2(∠AEB+∠ABE)=∠ACB+2∠ABE,
∴∠AEBACB,
故答案为:;
结论2:由结论1知,∠AEBACB,
∵∠ACB=90°,
∴∠AED∠ACB=45°,
∵EH⊥AF,
∴∠AEH=90°,
∴∠AEB=∠BEG=45°,
∵∠ABE=∠GBE,BE=BE,
∴△ABE≌△GBE(ASA),
∴AE=EG;
故答案为:AE=EG;
【应用结论】证明:(1)在Rt△AFC中,∠EFG+∠EAH=90°,
在Rt△AEH中,∠AHE+∠EAH=90°,
∴∠EFG=∠EHA,
在△EFG和△EHA中,
,
∴△EFG△EHA(AAS);
∴FG=HA;
(2)证明:补全图形如图所示,
在Rt△AEG中,
∵∠EAG=∠EGA=45°,
∴,
∴Rt△EFG≌Rt△EHA(HL),
∴EF=EH,
∵∠FEH=90°,
∴∠EFH=∠EHF=45°,
∴∠AFN=∠FAN=45°,∠NGH=∠AGE=45°,
∴FN=AN,∠NGH=∠NHG=45°,
∴GN=HN,
又∵AN=AG+GN,
∴.
12.【解答】解:图②的结论是BM2+NC2+BM NC=MN2.
证明:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
以点B为顶点在△ABC外作∠ABK=60°,在BK上截取BQ=CN,连接QA、QM,过点Q作QH⊥BC,垂足为H,
∵AB=AC,∠C=∠ABQ,CN=BQ,
∴△ACN≌△ABQ(SAS),
∴AN=AQ,∠CAN=∠QAB,
又∵∠CAN+∠BAM=30°,
∴∠BAM+∠QAB=30°,
即∠QAM=∠MAN,
又∵AM=AM,
∴△AQM≌△ANM(SAS),
∴MN=QM;
∵ABQ=60°,∠ABC=60°,
∴∠QBH=60°,
∴∠BQH=30°,
∴BHBQ,QHBQ,
∴HM=BM+BH=BMBQ,
在Rt△QHM中,可得:QH2+HM2=QM2,即(BQ)2+(BMBQ)2=QM2,
整理得BM2+BQ2+BM BQ=QM2.
∴BM2+NC2+BM NC=MN2.
图③的结论是:BM2+NC2﹣BM NC=MN2.
证明:以点B为顶点在△ABC外作∠ABK=30°,在BK上截取BQ=CN,连接QA、QM,过点Q作QH⊥BC,垂足为H,
∵AB=AC,∠C=∠ABQ,CN=BQ,
∴△ACN≌△ABQ(SAS),
∴AN=AQ,∠CAN=∠QAB,
又∵∠CAN+∠BAM=60°,
∴∠BAM+∠QAB=60°,即∠QAM=∠MAN,
又∵AM=AM,
∴△AQM≌△ANM(SAS),
∴MN=QM,
在Rt△BQH中,∠QBH=60°,∠BQH=30°,
∴BHBQ,QHBQ,
HM=BM﹣BH=BMBQ,
在Rt△QHM中,可得:QH2+HM2=QM2,即(BQ)2+(BMBQ)2=QM2,
整理得BM2+BQ2﹣BM BQ=QM2.
∴BM2+NC2﹣BM NC=MN2.
13.【解答】(1)证明:连接CD,
∵∠C=90°,AC=BC,AD=DB,
∴ABAC,∠A=∠B=∠ACD=45°,AD=CD=BD,CD⊥AB,
∵ED⊥FD,
∴∠EDF=∠CDB=90°,
∴∠CDE=∠BDF,
∴△CDE≌△BDF(ASA),
∴CE=BF,
∴AE+BF=AE+CE=ACAB;
(2)①AEBFAB,理由如下:
过点D作DN⊥AC于N,DH⊥BC于H,
∵∠C=90°,AC=BC,
∴∠A=∠B=45°,
∵DN⊥AC,DH⊥BC,
∴△ADN和△BDH是等腰直角三角形,
∴AN=DN,DH=BH,ADAN,BDBH,∠A=∠B=45°=∠ADN=∠BDH,
∴△ADN∽△BDH,
∴,
设AN=DN=x,BH=DH=2x,
∴ADx,BD=2x,
∴AB=3x,
∵DN⊥AC,DH⊥BC,∠ACB=90°,
∴四边形DHCN是矩形,
∴∠NDH=90°=∠EDF,
∴∠EDN=∠FDH,
又∵∠END=∠FHD,
∴△EDN∽△FDH,
∴,
∴FH=2NE,
∴AEBF=x+NE(2x﹣FH)=2xAB;
②如图4,当点F在射线BC上时,过点D作DN⊥AC于N,DH⊥BC于H,
∵∠C=90°,AC=BC,
∴∠A=∠B=45°,
∵DN⊥AC,DH⊥BC,
∴△ADN和△BDH是等腰直角三角形,
∴AN=DN,DH=BH,ADAN,BDBH,∠A=∠B=45°=∠ADN=∠BDH,
∴△ADN∽△BDH,
∴,
设AN=DN=x,BH=DH=nx,
∴ADx,BDnx,
∴AB(n+1)x,
∵DN⊥AC,DH⊥BC,∠ACB=90°,
∴四边形DHCN是矩形,
∴∠NDH=90°=∠EDF,
∴∠EDN=∠FDH,
又∵∠END=∠FHD,
∴△EDN∽△FDH,
∴,
∴FH=nNE,
∴AEBF=x﹣NE(nx+FH)=2xAB;
当点F在CB的延长线上时,如图5,
∵∠C=90°,AC=BC,
∴∠A=∠B=45°,
∵DN⊥AC,DH⊥BC,
∴△ADN和△BDH是等腰直角三角形,
∴AN=DN,DH=BH,ADAN,BDBH,∠A=∠B=45°=∠ADN=∠BDH,
∴△ADN∽△BDH,
∴,
设AN=DN=x,BH=DH=nx,
∴ADx,BDnx,
∴AB(n+1)x,
∵DN⊥AC,DH⊥BC,∠ACB=90°,
∴四边形DHCN是矩形,
∴∠NDH=90°=∠EDF,
∴∠EDN=∠FDH,
又∵∠END=∠FHD,
∴△EDN∽△FDH,
∴,
∴FH=nNE,
∴AEBF=x+NE(FH﹣nx)=2xAB;
综上所述:当点F在射线BC上时,,当点F在CB延长线上时,;
(3)如图,连接CD,CM,DM,
∵EF的中点为M,∠ACB=∠EDF=90°,
∴CM=DMEF,
∴点M在线段CD的垂直平分线上运动,
如图,当点E'与点A重合时,点F'在BC的延长线上,
当点E''与点C重合时,点F″在CB的延长线上,
过点M'作M'R⊥F'C于R,
∴M'R∥AC,
∴,
∴M'R=1,F'R=CR,
由图2,设AN=DN=x,BH=DH=nx,
∴ADx,BDnx,
∴AB(n+1)x=2,
∴x,
∵F'D=BDnx,
∴F'B=2nx,
∴CF'=2nx﹣2,
∴CR=nx﹣11,
由(2)可得:CDx ,DF″=nDE″=nx ,
∴CF″=(1+n2)x,
∴CM″,
∴RM″=n,
∴M″M',
∴点M运动的路径长为.
14.【解答】(1)证明:过点M作MQ∥BC,交AC于点Q,如图所示:
在等边△ABC中,∠A=∠B=∠ACB=60°,
∵MQ∥BC,
∴∠AMQ=∠B=60°,∠AQM=∠ACB=60°,∠QMP=∠N,
∴△AMQ是等边三角形,
∴AM=QM,
∵AM=CN,
∴QM=CN,
在△QMP和△CNP中,
,
∴△QMP≌△CNP(AAS),
∴MP=NP;
(2)解:∵△AMQ是等边三角形,且MH⊥AC,
∴AH=HQ,
∵△QMP≌△CNP,
∴QP=CP,
∴PH=HQ+QPAC,
∵AB=a,AB=AC,
∴PHa.
15.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠D=90°,BC=AD,
根据折叠的性质得:BC=CE,∠E=∠B=90°,
∴∠E=∠D=90°,AD=CE,
在△CEF与△ADF中,
,
∴△CEF≌△ADF(AAS);
(2)解:设DF=a,则CF=8﹣a,
∵四边形ABCD是矩形,
∴AB∥CD,AD=BC=x,
∴∠DCA=∠BAC,
根据折叠的性质得:∠EAC=∠BAC,
∴∠DCA=∠EAC,
∴AF=CF=8﹣a,
在Rt△ADF中,
∵AD2+DF2=AF2,
∴x2+a2=(8﹣a)2,
∴a,
∴tan∠DAF.
一、选择题
1.如图,在正方形ABCD的边CD上有一点E,连接AE,把AE绕点E逆时针旋转90°,得到FE,连接CF并延长与AB的延长线交于点G.则的值为( )
A. B. C. D.
2.如图,在△ABC中,D是AC的中点,CE⊥AB,BD与CE交于点O,且BE=CD.下列说法错误的是( )
A.BD的垂直平分线一定与AB相交于点E
B.∠BDC=3∠ABD
C.当E为AB中点时,△ABC是等边三角形
D.当E为AB中点时,
3.如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,E分别在AC,BC边上运动,连结AE,BD交于点F,且始终满足ADCE,则下列结论:①;②∠DFE=135°;③△ABF面积的最大值是44;④CF的最小值是22.其中正确的是( )
A.①③ B.①②④ C.②③④ D.①②③④
4.如图,在菱形ABCD中,∠ABC=60°,AB=1,点P是BC边上一个动点,在BC延长线上找一点Q,使得点P和点Q关于点C对称,连结DP、AQ交于点M.当点P从B点运动到C点时,点M的运动路径长为( )
A. B. C. D.
5.我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则sinθ=( )
A. B. C. D.
二、填空题
6.如图,在△ABC中,AE1,BE1分别是内角∠CAB,外角∠CBD的三等分线,且∠E1AD∠CAB,∠E1BD∠CBD,在△ABE1中,AE2,BE2分别是内角∠E1AB,外角∠E1BD的三等分线,且∠E2AD∠E1AB,∠E2BD∠E1BD,…,以此规律作下去,若∠C=m°,则∠En= 度.
7.如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 ;(2)DG的长是 .
8.如图,四边形ABCD的两条对角线AC,BD互相垂直,AC=4,BD=6,则AD+BC的最小值是 .
9.如图,DE平分等边△ABC的面积,折叠△BDE得到△FDE,AC分别与DF,EF相交于G,H两点.若DG=m,EH=n,用含m,n的式子表示GH的长是 .
10.如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a,DF=b,连接AE,BE,若△ADE与△BEH的面积相等,则 .
三、解答题
11.综合与实践
如图1,在△ABC中,BD是∠ABC的平分线,BD的延长线交外角∠CAM的平分线于点E.
【发现结论】
结论1:∠AEB= ∠ACB;
结论2:当图1中∠ACB=90°时,如图2所示,延长BC交AE于点F,过点E作AF的垂线交BF于点G,交AC的延长线于点H.则AE与EG的数量关系是 .
【应用结论】
(1)求证:AH=GF;
(2)在图2中连接FH,AG,延长AG交FH于点N,补全图形,求证:.
12.已知△ABC是等腰三角形,AB=AC,∠MAN∠BAC,∠MAN在∠BAC的内部,点M、N在BC上,点M在点N的左侧,探究线段BM、NC、MN之间的数量关系.
(1)如图①,当∠BAC=90°时,探究如下:
由∠BAC=90°,AB=AC可知,将△ACN绕点A顺时针旋转90°,得到△ABP,则CN=BP且∠PBM=90°,连接PM,易证△AMP≌△AMN,可得MP=MN,在Rt△PBM中,BM2+BP2=MP2,则有BM2+NC2=MN2.
(2)当∠BAC=60°时,如图②:当∠BAC=120°时,如图③,分别写出线段BM、NC、MN之间的数量关系,并选择图②或图③进行证明.
13.探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
在Rt△ABC中,∠C=90°,AC=BC,D是AB边上一点,且(n为正整数),E是AC边上的动点,过点D作DE的垂线交直线BC于点F.
【初步感知】
(1)如图1,当n=1时,兴趣小组探究得出结论:AE+BFAB,请写出证明过程.
【深入探究】
(2)①如图2,当n=2,且点F在线段BC上时,试探究线段AE,BF,AB之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段AE,BF,AB之间数量关系的一般结论(直接写出结论,不必证明).
【拓展运用】
(3)如图3,连接EF,设EF的中点为M,若AB=2,求点E从点A运动到点C的过程中,点M运动的路径长(用含n的代数式表示).
14.如图,在等边三角形ABC中,点M为AB边上任意一点,延长BC至点N,使CN=AM,连接MN交AC于点P,MH⊥AC于点H.
(1)求证:MP=NP;
(2)若AB=a,求线段PH的长(结果用含a的代数式表示).
15.如图,已知矩形ABCD中,AB=8,BC=x(0<x<8),将△ACB沿AC对折到△ACE的位置,AE和CD交于点F.
(1)求证:△CEF≌△ADF;
(2)求tan∠DAF的值(用含x的式子表示).
参考答案
一、选择题
题号 1 2 3 4 5
答案 A D D B A
二、填空题
6.答案为:.
7. 30° ;.
8.答案为:.
9.答案为:.
10.答案为:3.
三、解答题
11.【解答】【发现结论】解:结论1:∵BD是∠ABC的平分线,
∴∠ABC=2∠ABE,
∵AE是∠CAM的平分线,
∴∠CAM=2∠EAM,
∵∠CAM=∠ACB+∠ABC,
∴2∠EAM=∠ACB+2∠ABE,
∵∠EAM=∠AEB+∠ABE,
∴2(∠AEB+∠ABE)=∠ACB+2∠ABE,
∴∠AEBACB,
故答案为:;
结论2:由结论1知,∠AEBACB,
∵∠ACB=90°,
∴∠AED∠ACB=45°,
∵EH⊥AF,
∴∠AEH=90°,
∴∠AEB=∠BEG=45°,
∵∠ABE=∠GBE,BE=BE,
∴△ABE≌△GBE(ASA),
∴AE=EG;
故答案为:AE=EG;
【应用结论】证明:(1)在Rt△AFC中,∠EFG+∠EAH=90°,
在Rt△AEH中,∠AHE+∠EAH=90°,
∴∠EFG=∠EHA,
在△EFG和△EHA中,
,
∴△EFG△EHA(AAS);
∴FG=HA;
(2)证明:补全图形如图所示,
在Rt△AEG中,
∵∠EAG=∠EGA=45°,
∴,
∴Rt△EFG≌Rt△EHA(HL),
∴EF=EH,
∵∠FEH=90°,
∴∠EFH=∠EHF=45°,
∴∠AFN=∠FAN=45°,∠NGH=∠AGE=45°,
∴FN=AN,∠NGH=∠NHG=45°,
∴GN=HN,
又∵AN=AG+GN,
∴.
12.【解答】解:图②的结论是BM2+NC2+BM NC=MN2.
证明:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
以点B为顶点在△ABC外作∠ABK=60°,在BK上截取BQ=CN,连接QA、QM,过点Q作QH⊥BC,垂足为H,
∵AB=AC,∠C=∠ABQ,CN=BQ,
∴△ACN≌△ABQ(SAS),
∴AN=AQ,∠CAN=∠QAB,
又∵∠CAN+∠BAM=30°,
∴∠BAM+∠QAB=30°,
即∠QAM=∠MAN,
又∵AM=AM,
∴△AQM≌△ANM(SAS),
∴MN=QM;
∵ABQ=60°,∠ABC=60°,
∴∠QBH=60°,
∴∠BQH=30°,
∴BHBQ,QHBQ,
∴HM=BM+BH=BMBQ,
在Rt△QHM中,可得:QH2+HM2=QM2,即(BQ)2+(BMBQ)2=QM2,
整理得BM2+BQ2+BM BQ=QM2.
∴BM2+NC2+BM NC=MN2.
图③的结论是:BM2+NC2﹣BM NC=MN2.
证明:以点B为顶点在△ABC外作∠ABK=30°,在BK上截取BQ=CN,连接QA、QM,过点Q作QH⊥BC,垂足为H,
∵AB=AC,∠C=∠ABQ,CN=BQ,
∴△ACN≌△ABQ(SAS),
∴AN=AQ,∠CAN=∠QAB,
又∵∠CAN+∠BAM=60°,
∴∠BAM+∠QAB=60°,即∠QAM=∠MAN,
又∵AM=AM,
∴△AQM≌△ANM(SAS),
∴MN=QM,
在Rt△BQH中,∠QBH=60°,∠BQH=30°,
∴BHBQ,QHBQ,
HM=BM﹣BH=BMBQ,
在Rt△QHM中,可得:QH2+HM2=QM2,即(BQ)2+(BMBQ)2=QM2,
整理得BM2+BQ2﹣BM BQ=QM2.
∴BM2+NC2﹣BM NC=MN2.
13.【解答】(1)证明:连接CD,
∵∠C=90°,AC=BC,AD=DB,
∴ABAC,∠A=∠B=∠ACD=45°,AD=CD=BD,CD⊥AB,
∵ED⊥FD,
∴∠EDF=∠CDB=90°,
∴∠CDE=∠BDF,
∴△CDE≌△BDF(ASA),
∴CE=BF,
∴AE+BF=AE+CE=ACAB;
(2)①AEBFAB,理由如下:
过点D作DN⊥AC于N,DH⊥BC于H,
∵∠C=90°,AC=BC,
∴∠A=∠B=45°,
∵DN⊥AC,DH⊥BC,
∴△ADN和△BDH是等腰直角三角形,
∴AN=DN,DH=BH,ADAN,BDBH,∠A=∠B=45°=∠ADN=∠BDH,
∴△ADN∽△BDH,
∴,
设AN=DN=x,BH=DH=2x,
∴ADx,BD=2x,
∴AB=3x,
∵DN⊥AC,DH⊥BC,∠ACB=90°,
∴四边形DHCN是矩形,
∴∠NDH=90°=∠EDF,
∴∠EDN=∠FDH,
又∵∠END=∠FHD,
∴△EDN∽△FDH,
∴,
∴FH=2NE,
∴AEBF=x+NE(2x﹣FH)=2xAB;
②如图4,当点F在射线BC上时,过点D作DN⊥AC于N,DH⊥BC于H,
∵∠C=90°,AC=BC,
∴∠A=∠B=45°,
∵DN⊥AC,DH⊥BC,
∴△ADN和△BDH是等腰直角三角形,
∴AN=DN,DH=BH,ADAN,BDBH,∠A=∠B=45°=∠ADN=∠BDH,
∴△ADN∽△BDH,
∴,
设AN=DN=x,BH=DH=nx,
∴ADx,BDnx,
∴AB(n+1)x,
∵DN⊥AC,DH⊥BC,∠ACB=90°,
∴四边形DHCN是矩形,
∴∠NDH=90°=∠EDF,
∴∠EDN=∠FDH,
又∵∠END=∠FHD,
∴△EDN∽△FDH,
∴,
∴FH=nNE,
∴AEBF=x﹣NE(nx+FH)=2xAB;
当点F在CB的延长线上时,如图5,
∵∠C=90°,AC=BC,
∴∠A=∠B=45°,
∵DN⊥AC,DH⊥BC,
∴△ADN和△BDH是等腰直角三角形,
∴AN=DN,DH=BH,ADAN,BDBH,∠A=∠B=45°=∠ADN=∠BDH,
∴△ADN∽△BDH,
∴,
设AN=DN=x,BH=DH=nx,
∴ADx,BDnx,
∴AB(n+1)x,
∵DN⊥AC,DH⊥BC,∠ACB=90°,
∴四边形DHCN是矩形,
∴∠NDH=90°=∠EDF,
∴∠EDN=∠FDH,
又∵∠END=∠FHD,
∴△EDN∽△FDH,
∴,
∴FH=nNE,
∴AEBF=x+NE(FH﹣nx)=2xAB;
综上所述:当点F在射线BC上时,,当点F在CB延长线上时,;
(3)如图,连接CD,CM,DM,
∵EF的中点为M,∠ACB=∠EDF=90°,
∴CM=DMEF,
∴点M在线段CD的垂直平分线上运动,
如图,当点E'与点A重合时,点F'在BC的延长线上,
当点E''与点C重合时,点F″在CB的延长线上,
过点M'作M'R⊥F'C于R,
∴M'R∥AC,
∴,
∴M'R=1,F'R=CR,
由图2,设AN=DN=x,BH=DH=nx,
∴ADx,BDnx,
∴AB(n+1)x=2,
∴x,
∵F'D=BDnx,
∴F'B=2nx,
∴CF'=2nx﹣2,
∴CR=nx﹣11,
由(2)可得:CDx ,DF″=nDE″=nx ,
∴CF″=(1+n2)x,
∴CM″,
∴RM″=n,
∴M″M',
∴点M运动的路径长为.
14.【解答】(1)证明:过点M作MQ∥BC,交AC于点Q,如图所示:
在等边△ABC中,∠A=∠B=∠ACB=60°,
∵MQ∥BC,
∴∠AMQ=∠B=60°,∠AQM=∠ACB=60°,∠QMP=∠N,
∴△AMQ是等边三角形,
∴AM=QM,
∵AM=CN,
∴QM=CN,
在△QMP和△CNP中,
,
∴△QMP≌△CNP(AAS),
∴MP=NP;
(2)解:∵△AMQ是等边三角形,且MH⊥AC,
∴AH=HQ,
∵△QMP≌△CNP,
∴QP=CP,
∴PH=HQ+QPAC,
∵AB=a,AB=AC,
∴PHa.
15.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠D=90°,BC=AD,
根据折叠的性质得:BC=CE,∠E=∠B=90°,
∴∠E=∠D=90°,AD=CE,
在△CEF与△ADF中,
,
∴△CEF≌△ADF(AAS);
(2)解:设DF=a,则CF=8﹣a,
∵四边形ABCD是矩形,
∴AB∥CD,AD=BC=x,
∴∠DCA=∠BAC,
根据折叠的性质得:∠EAC=∠BAC,
∴∠DCA=∠EAC,
∴AF=CF=8﹣a,
在Rt△ADF中,
∵AD2+DF2=AF2,
∴x2+a2=(8﹣a)2,
∴a,
∴tan∠DAF.
同课章节目录
