2025年九年级数学中考三轮冲刺练习二次函数的应用练习(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺练习二次函数的应用练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 491.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 10:43:35 | ||
图片预览




文档简介
2025年九年级数学中考三轮冲刺练习二次函数的应用练习
一、选择题
1.坐落于开封清明上河园中的虹桥是一座抛物线型拱桥,被列为中国十大名桥之一.按如图所示建立平面直角坐标系,得到抛物线解析式为,正常水位时水面宽AB为16m,当水位上升3m时,水面宽CD为( )
A.4m B.8m C.10m D.12m
2.图1是一个横断面为抛物线形状的拱桥,当水面在L时,拱顶(拱桥洞的最高点)离水面2m,水面宽为4m.如果水面宽度为6m,则水面下降( )
A.3.5m B.3m C.2.5m D.2m
3.日渐强大的祖国给了我们安静祥和的学习环境.我国某集团军在一次炮弹发射演习中,记录到一门迫击炮发射的炮弹的飞行高度y(米)与飞行时间x(秒)之间的关系式为,一枚炮弹从发射到落地,经过的时间为( )
A.10秒 B.25秒 C.50秒 D.100秒
4.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为.则CD的长为( )m.
A.18 B.20 C.22 D.30
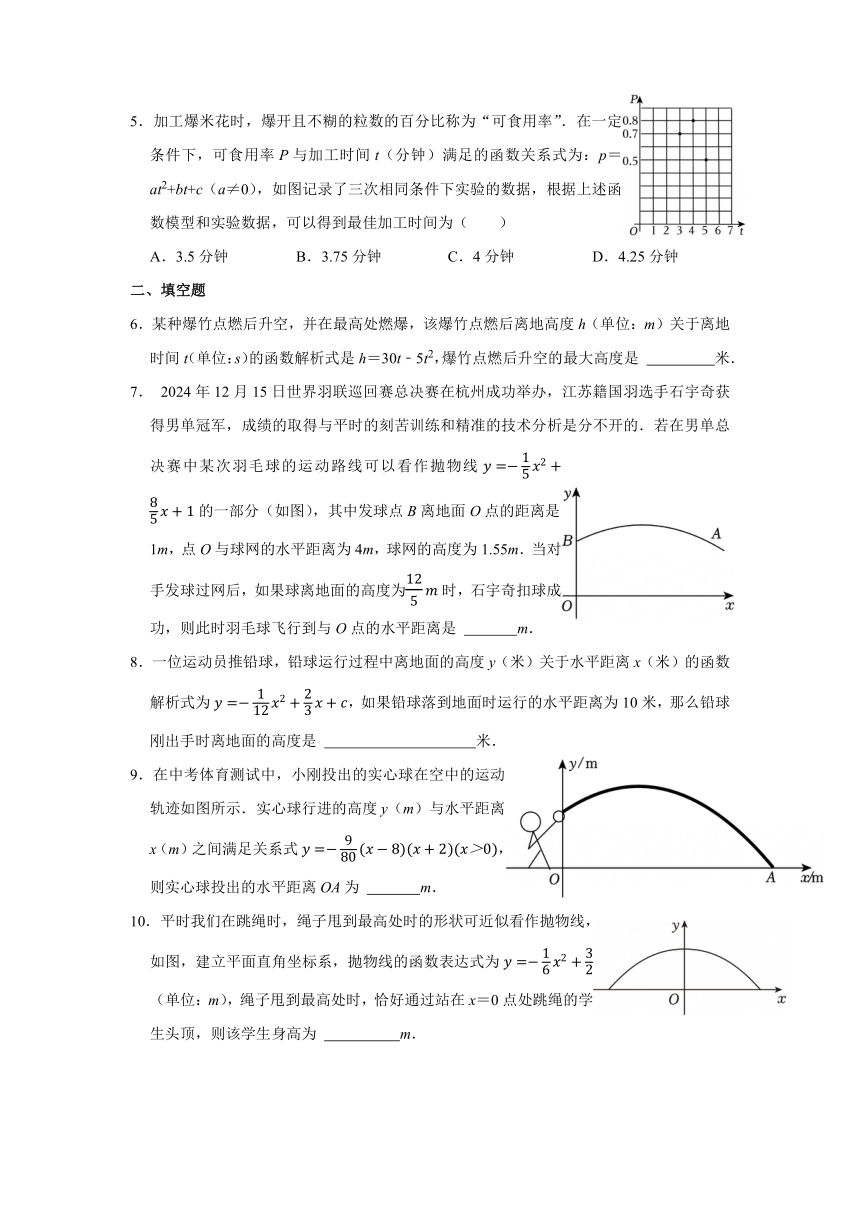
5.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在一定条件下,可食用率P与加工时间t(分钟)满足的函数关系式为:p=at2+bt+c(a≠0),如图记录了三次相同条件下实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为( )
A.3.5分钟 B.3.75分钟 C.4分钟 D.4.25分钟
二、填空题
6.某种爆竹点燃后升空,并在最高处燃爆,该爆竹点燃后离地高度h(单位:m)关于离地时间t(单位:s)的函数解析式是h=30t﹣5t2,爆竹点燃后升空的最大高度是 米.
7. 2024年12月15日世界羽联巡回赛总决赛在杭州成功举办,江苏籍国羽选手石宇奇获得男单冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.若在男单总决赛中某次羽毛球的运动路线可以看作抛物线的一部分(如图),其中发球点B离地面O点的距离是1m,点O与球网的水平距离为4m,球网的高度为1.55m.当对手发球过网后,如果球离地面的高度为时,石宇奇扣球成功,则此时羽毛球飞行到与O点的水平距离是 m.
8.一位运动员推铅球,铅球运行过程中离地面的高度y(米)关于水平距离x(米)的函数解析式为,如果铅球落到地面时运行的水平距离为10米,那么铅球刚出手时离地面的高度是 米.
9.在中考体育测试中,小刚投出的实心球在空中的运动轨迹如图所示.实心球行进的高度y(m)与水平距离x(m)之间满足关系式,则实心球投出的水平距离OA为 m.
10.平时我们在跳绳时,绳子甩到最高处时的形状可近似看作抛物线,如图,建立平面直角坐标系,抛物线的函数表达式为(单位:m),绳子甩到最高处时,恰好通过站在x=0点处跳绳的学生头顶,则该学生身高为 m.
三、解答题
11.某食品经销商购进一种食品若干千克,成本价为每千克30元,物价部门规定其销售单价不得低于成本价,且不得高于成本价的2倍.经市场调研发现,日销售量y(千克)与销售单价x(元)符合一次函数关系,如图所示:
(1)求y与x之间的函数关系式;
(2)在销售过程中,当销售单价为多少元时,该经销商每天获得的利润最大?最大利润是多少元?
12.某兴趣小组做小球弹射实验,x轴表示水平地面,Rt△ABC表示斜坡,∠ACB=90°.从O点处以一定方向和速度弹出小球,小球的飞行路线可用抛物线y=ax2+bx刻画,其中x为小球弹出后飞行的水平距离,y为小球弹出后距离水平地面的高度.斜面AB可用直线y=kx+m刻画.实验测得:OA=2,BC=4,AC=8;小球飞行过程中经过、(4,8)和三个点.
(1)求抛物线y=ax2+bx的表达式;
(2)求小球在斜面AB上的落点Q的横坐标;
(3)当x>2时,小球在飞行过程中与斜面AB间的竖直距离PH的最大值为多少?
13.16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.
某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系,分别得到抛物线y=ax2+x和直线yx+b.其中,当火箭运行的水平距离为9km时,自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35km,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15km.
14.如图,一小球从斜坡O点以一定的方向弹出,球的飞行路线可以用二次函数y=ax2+bx(a<0)刻画,斜坡可以用一次函数刻画,小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律如表:
x 0 1 2 m 4 5 6 7 …
y 0 6 8 n …
(1)①m= ,n= ;
②小球的落点是A,求点A的坐标.
(2)小球飞行高度y(米)与飞行时间t(秒)满足关系:y=﹣5t2+vt.
①小球飞行的最大高度为 米;
②求v的值.
15.某企业准备对A,B两个生产性项目进行投资,根据其生产成本、销售情况等因素进行分析得知:投资A项目一年后的收益yA(万元)与投入资金x(万元)的函数表达式为:yAx,投资B项目一年后的收益yB(万元)与投入资金x(万元)的函数表达式为:yBx2+2x.
(1)若将10万元资金投入A项目,一年后获得的收益是多少?
(2)若对A,B两个项目投入相同的资金m(m>0)万元,一年后两者获得的收益相等,则m的值是多少?
(3)2025年,我国对小微企业施行所得税优惠政策.该企业将根据此政策获得的减免税款及其他结余资金共计32万元,全部投入到A,B两个项目中,当A,B两个项目分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?
参考答案
一、选择题
题号 1 2 3 4 5
答案 B C C C B
二、填空题
6.【解答】解:h=30t﹣5t2=﹣5(t2﹣6t+9)+45=﹣5(t﹣3)2+45,
依据顶点式可知顶点坐坐标为(3,45),则最大值为45.
故答案为:45.
7. 【解答】解:由题意得:把y代入中得:x2x+1,
整理得:x2﹣8x+7=0,
解得:x1=7,x2=1(舍去),
∴此时羽毛球飞行到与O点的水平距离是7m,
故答案为:7.
8.【解答】解:∵铅球落到地面时运行的水平距离为10米,
∴抛物线经过点(10,0),
∴10210+c=0,
解得:c,
∴yx2x,
当x=0时,y.
∴铅球刚出手时离地面的高度是米.
故答案为:.
9.【解答】解:令y=0,则(x﹣8)(x+2)=0,
解得x=8或x=﹣2(舍去),
∴实心球从起点到落地点的水平距离为8m,
故答案为:8.
10..【解答】解:将x=0代入,yx2,y=01.5m,则该学生身高为1.5m,故答案为:1.5.
三、解答题
11.【解答】解:(1)设y=kx+b,
把(30,80),(50,40)代入y=kx+b中得:
,
解得:,
∴y与x之间的函数关系式:y=﹣2x+140;
(2)设总利润为w元,
由题意得:w=y(x﹣30)
=(﹣2x+140)(x﹣30)
=﹣2x2+200x﹣4200
=﹣2(x﹣50)2+800,
∵a=﹣2<0,且30≤x≤60,
∴当x=50时,w最大=800元,
∴在销售过程中,当销售单价为50元时,该经销商每天获得的利润最大,最大利润是800元.
12.【解答】解:(1)将、(4,8)代入y=ax2+bx得,
,
解得,
∴抛物线的表达式为yx2+4x;
(2)∵OA=2,BC=4,AC=8,
∴A(2,0),B(10,4),
将A、B坐标代入y=kx+m得,
,
解得,
∴斜面AB的解析式为yx﹣1,
∵小球在斜面AB上的落点Q可以看作是斜面AB和抛物线的交点,
∴令x2+4xx﹣1,
解得x(负值舍去),
∴点Q的横坐标为;
(3)设P的坐标为(p,p2+4p),则H(p,p﹣1),P>2,
∴PHp2+4pP+1P2P+1,
∵0,
∴当p时,PH有最大值,
此时PH()21,
答:小球在飞行过程中与斜面AB间的竖直距离PH的最大值为.
13.【解答】解:(1)①∵y=ax2+x经过点(9,3.6),
∴81a+9=3.6.
解得:a.
∵yx+b经过点(9,3.6),
∴3.69+b.
解得:b=8.1;
②由①得:yx2+x
(x2﹣15x)
(x)2(0≤x≤9).
∴火箭运行的最高点是km.
∴1.35=2.4(km).
∴2.4x2+x.
整理得:x2﹣15x+36=0.
解得:x1=12>9(不合题意,舍去),x2=3.
由①得:yx+8.1.
∴2.4x+8.1.
解得:x=11.4.
∴11.4﹣3=8.4(km).
答:这两个位置之间的距离为8.4km;
(2)当x=9时,y=81a+9.
∴火箭第二级的引发点的坐标为(9,81a+9).
设火箭落地点与发射点的水平距离为15km.
∴yx+b经过点(9,81a+9),(15,0)
∴.
解得:.
∴a<0时,火箭落地点与发射点的水平距离超过15km.
14.【解答】解:(1)①根据小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律表可知,
抛物线顶点坐标为(4,8),
,
解得:,
∴二次函数解析式为yx2+4x,
当y时,x2+4x,
解得:x=3或x=5(舍去),
∴m=3,
当x=6时,n=y62+4×6=6,
故答案为:3,6.
②联立得:,
解得:或,
∴点A的坐标是(,).
(2)①由题干可知小球飞行最大高度为8米,
故答案为:8.
②y=﹣5t2+vt=﹣5(t)2,
则8,
解得v=4(负值舍去).
15.【解答】解:(1)当x=10时,yA(万元),
答:将10万元资金投入A项目,一年后获得的收益是4万元;
(2)由题意得:当x=m时,yA=yB,
∴
∴m1=8,m2=0(舍去),
∴m=8;
(3)设投入B项目的资金是t万元,投入A项目的资金(32﹣t),一年后获利为W万元,
由题意得,
W,
∴当t=4时,W最大=16,
32﹣t=28(万元),
∴投入A项目的资金是28万元,投入B项目的资金4万元时,一年后获利最大.最大值是16万元.
一、选择题
1.坐落于开封清明上河园中的虹桥是一座抛物线型拱桥,被列为中国十大名桥之一.按如图所示建立平面直角坐标系,得到抛物线解析式为,正常水位时水面宽AB为16m,当水位上升3m时,水面宽CD为( )
A.4m B.8m C.10m D.12m
2.图1是一个横断面为抛物线形状的拱桥,当水面在L时,拱顶(拱桥洞的最高点)离水面2m,水面宽为4m.如果水面宽度为6m,则水面下降( )
A.3.5m B.3m C.2.5m D.2m
3.日渐强大的祖国给了我们安静祥和的学习环境.我国某集团军在一次炮弹发射演习中,记录到一门迫击炮发射的炮弹的飞行高度y(米)与飞行时间x(秒)之间的关系式为,一枚炮弹从发射到落地,经过的时间为( )
A.10秒 B.25秒 C.50秒 D.100秒
4.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为.则CD的长为( )m.
A.18 B.20 C.22 D.30
5.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在一定条件下,可食用率P与加工时间t(分钟)满足的函数关系式为:p=at2+bt+c(a≠0),如图记录了三次相同条件下实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为( )
A.3.5分钟 B.3.75分钟 C.4分钟 D.4.25分钟
二、填空题
6.某种爆竹点燃后升空,并在最高处燃爆,该爆竹点燃后离地高度h(单位:m)关于离地时间t(单位:s)的函数解析式是h=30t﹣5t2,爆竹点燃后升空的最大高度是 米.
7. 2024年12月15日世界羽联巡回赛总决赛在杭州成功举办,江苏籍国羽选手石宇奇获得男单冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.若在男单总决赛中某次羽毛球的运动路线可以看作抛物线的一部分(如图),其中发球点B离地面O点的距离是1m,点O与球网的水平距离为4m,球网的高度为1.55m.当对手发球过网后,如果球离地面的高度为时,石宇奇扣球成功,则此时羽毛球飞行到与O点的水平距离是 m.
8.一位运动员推铅球,铅球运行过程中离地面的高度y(米)关于水平距离x(米)的函数解析式为,如果铅球落到地面时运行的水平距离为10米,那么铅球刚出手时离地面的高度是 米.
9.在中考体育测试中,小刚投出的实心球在空中的运动轨迹如图所示.实心球行进的高度y(m)与水平距离x(m)之间满足关系式,则实心球投出的水平距离OA为 m.
10.平时我们在跳绳时,绳子甩到最高处时的形状可近似看作抛物线,如图,建立平面直角坐标系,抛物线的函数表达式为(单位:m),绳子甩到最高处时,恰好通过站在x=0点处跳绳的学生头顶,则该学生身高为 m.
三、解答题
11.某食品经销商购进一种食品若干千克,成本价为每千克30元,物价部门规定其销售单价不得低于成本价,且不得高于成本价的2倍.经市场调研发现,日销售量y(千克)与销售单价x(元)符合一次函数关系,如图所示:
(1)求y与x之间的函数关系式;
(2)在销售过程中,当销售单价为多少元时,该经销商每天获得的利润最大?最大利润是多少元?
12.某兴趣小组做小球弹射实验,x轴表示水平地面,Rt△ABC表示斜坡,∠ACB=90°.从O点处以一定方向和速度弹出小球,小球的飞行路线可用抛物线y=ax2+bx刻画,其中x为小球弹出后飞行的水平距离,y为小球弹出后距离水平地面的高度.斜面AB可用直线y=kx+m刻画.实验测得:OA=2,BC=4,AC=8;小球飞行过程中经过、(4,8)和三个点.
(1)求抛物线y=ax2+bx的表达式;
(2)求小球在斜面AB上的落点Q的横坐标;
(3)当x>2时,小球在飞行过程中与斜面AB间的竖直距离PH的最大值为多少?
13.16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.
某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系,分别得到抛物线y=ax2+x和直线yx+b.其中,当火箭运行的水平距离为9km时,自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35km,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15km.
14.如图,一小球从斜坡O点以一定的方向弹出,球的飞行路线可以用二次函数y=ax2+bx(a<0)刻画,斜坡可以用一次函数刻画,小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律如表:
x 0 1 2 m 4 5 6 7 …
y 0 6 8 n …
(1)①m= ,n= ;
②小球的落点是A,求点A的坐标.
(2)小球飞行高度y(米)与飞行时间t(秒)满足关系:y=﹣5t2+vt.
①小球飞行的最大高度为 米;
②求v的值.
15.某企业准备对A,B两个生产性项目进行投资,根据其生产成本、销售情况等因素进行分析得知:投资A项目一年后的收益yA(万元)与投入资金x(万元)的函数表达式为:yAx,投资B项目一年后的收益yB(万元)与投入资金x(万元)的函数表达式为:yBx2+2x.
(1)若将10万元资金投入A项目,一年后获得的收益是多少?
(2)若对A,B两个项目投入相同的资金m(m>0)万元,一年后两者获得的收益相等,则m的值是多少?
(3)2025年,我国对小微企业施行所得税优惠政策.该企业将根据此政策获得的减免税款及其他结余资金共计32万元,全部投入到A,B两个项目中,当A,B两个项目分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?
参考答案
一、选择题
题号 1 2 3 4 5
答案 B C C C B
二、填空题
6.【解答】解:h=30t﹣5t2=﹣5(t2﹣6t+9)+45=﹣5(t﹣3)2+45,
依据顶点式可知顶点坐坐标为(3,45),则最大值为45.
故答案为:45.
7. 【解答】解:由题意得:把y代入中得:x2x+1,
整理得:x2﹣8x+7=0,
解得:x1=7,x2=1(舍去),
∴此时羽毛球飞行到与O点的水平距离是7m,
故答案为:7.
8.【解答】解:∵铅球落到地面时运行的水平距离为10米,
∴抛物线经过点(10,0),
∴10210+c=0,
解得:c,
∴yx2x,
当x=0时,y.
∴铅球刚出手时离地面的高度是米.
故答案为:.
9.【解答】解:令y=0,则(x﹣8)(x+2)=0,
解得x=8或x=﹣2(舍去),
∴实心球从起点到落地点的水平距离为8m,
故答案为:8.
10..【解答】解:将x=0代入,yx2,y=01.5m,则该学生身高为1.5m,故答案为:1.5.
三、解答题
11.【解答】解:(1)设y=kx+b,
把(30,80),(50,40)代入y=kx+b中得:
,
解得:,
∴y与x之间的函数关系式:y=﹣2x+140;
(2)设总利润为w元,
由题意得:w=y(x﹣30)
=(﹣2x+140)(x﹣30)
=﹣2x2+200x﹣4200
=﹣2(x﹣50)2+800,
∵a=﹣2<0,且30≤x≤60,
∴当x=50时,w最大=800元,
∴在销售过程中,当销售单价为50元时,该经销商每天获得的利润最大,最大利润是800元.
12.【解答】解:(1)将、(4,8)代入y=ax2+bx得,
,
解得,
∴抛物线的表达式为yx2+4x;
(2)∵OA=2,BC=4,AC=8,
∴A(2,0),B(10,4),
将A、B坐标代入y=kx+m得,
,
解得,
∴斜面AB的解析式为yx﹣1,
∵小球在斜面AB上的落点Q可以看作是斜面AB和抛物线的交点,
∴令x2+4xx﹣1,
解得x(负值舍去),
∴点Q的横坐标为;
(3)设P的坐标为(p,p2+4p),则H(p,p﹣1),P>2,
∴PHp2+4pP+1P2P+1,
∵0,
∴当p时,PH有最大值,
此时PH()21,
答:小球在飞行过程中与斜面AB间的竖直距离PH的最大值为.
13.【解答】解:(1)①∵y=ax2+x经过点(9,3.6),
∴81a+9=3.6.
解得:a.
∵yx+b经过点(9,3.6),
∴3.69+b.
解得:b=8.1;
②由①得:yx2+x
(x2﹣15x)
(x)2(0≤x≤9).
∴火箭运行的最高点是km.
∴1.35=2.4(km).
∴2.4x2+x.
整理得:x2﹣15x+36=0.
解得:x1=12>9(不合题意,舍去),x2=3.
由①得:yx+8.1.
∴2.4x+8.1.
解得:x=11.4.
∴11.4﹣3=8.4(km).
答:这两个位置之间的距离为8.4km;
(2)当x=9时,y=81a+9.
∴火箭第二级的引发点的坐标为(9,81a+9).
设火箭落地点与发射点的水平距离为15km.
∴yx+b经过点(9,81a+9),(15,0)
∴.
解得:.
∴a<0时,火箭落地点与发射点的水平距离超过15km.
14.【解答】解:(1)①根据小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律表可知,
抛物线顶点坐标为(4,8),
,
解得:,
∴二次函数解析式为yx2+4x,
当y时,x2+4x,
解得:x=3或x=5(舍去),
∴m=3,
当x=6时,n=y62+4×6=6,
故答案为:3,6.
②联立得:,
解得:或,
∴点A的坐标是(,).
(2)①由题干可知小球飞行最大高度为8米,
故答案为:8.
②y=﹣5t2+vt=﹣5(t)2,
则8,
解得v=4(负值舍去).
15.【解答】解:(1)当x=10时,yA(万元),
答:将10万元资金投入A项目,一年后获得的收益是4万元;
(2)由题意得:当x=m时,yA=yB,
∴
∴m1=8,m2=0(舍去),
∴m=8;
(3)设投入B项目的资金是t万元,投入A项目的资金(32﹣t),一年后获利为W万元,
由题意得,
W,
∴当t=4时,W最大=16,
32﹣t=28(万元),
∴投入A项目的资金是28万元,投入B项目的资金4万元时,一年后获利最大.最大值是16万元.
同课章节目录
