2025年九年级中考数学三轮冲刺练习圆中相似三角形和锐角三角函数综合练习(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习圆中相似三角形和锐角三角函数综合练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 12:30:42 | ||
图片预览


文档简介
2025年九年级中考数学三轮冲刺练习圆中相似三角形和锐角三角函数综合练习
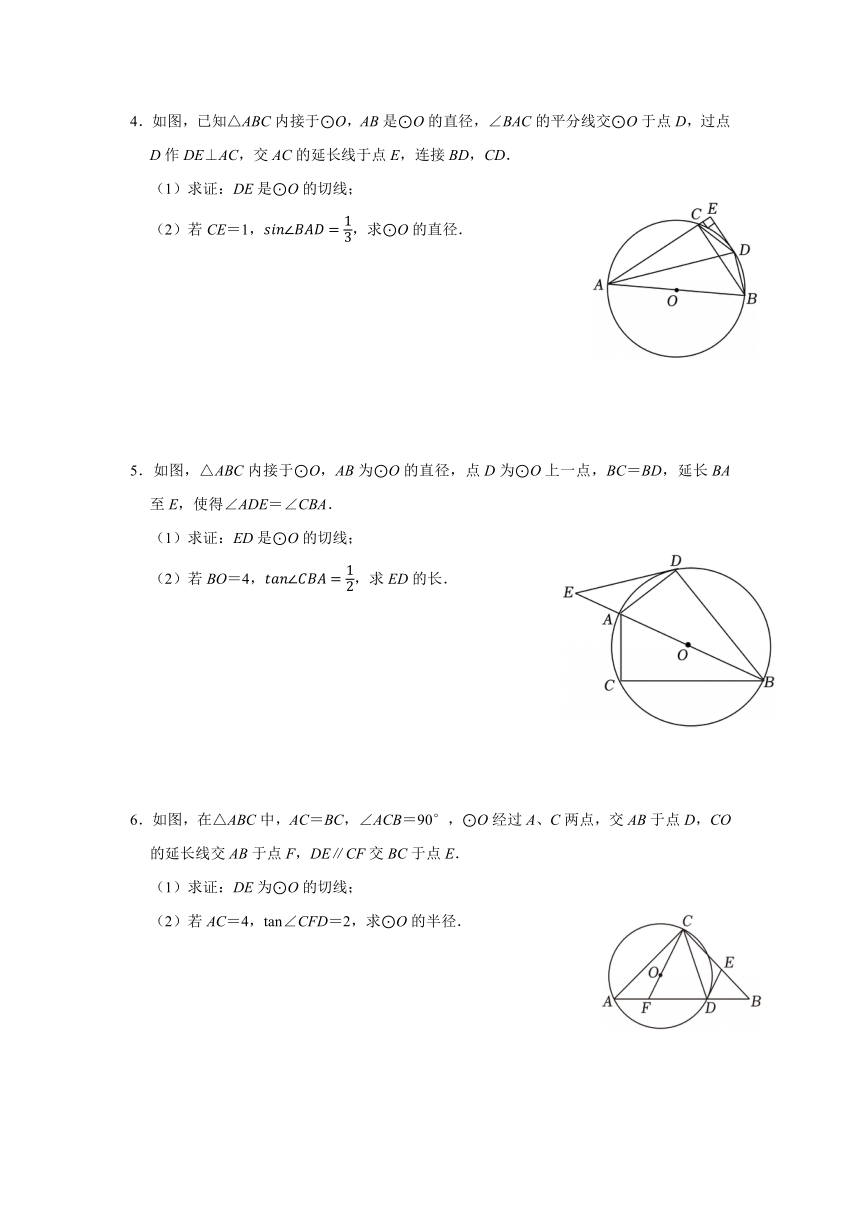
1.如图,△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,交AB的延长线于点E,垂足为点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AB=18,,求BE的长.
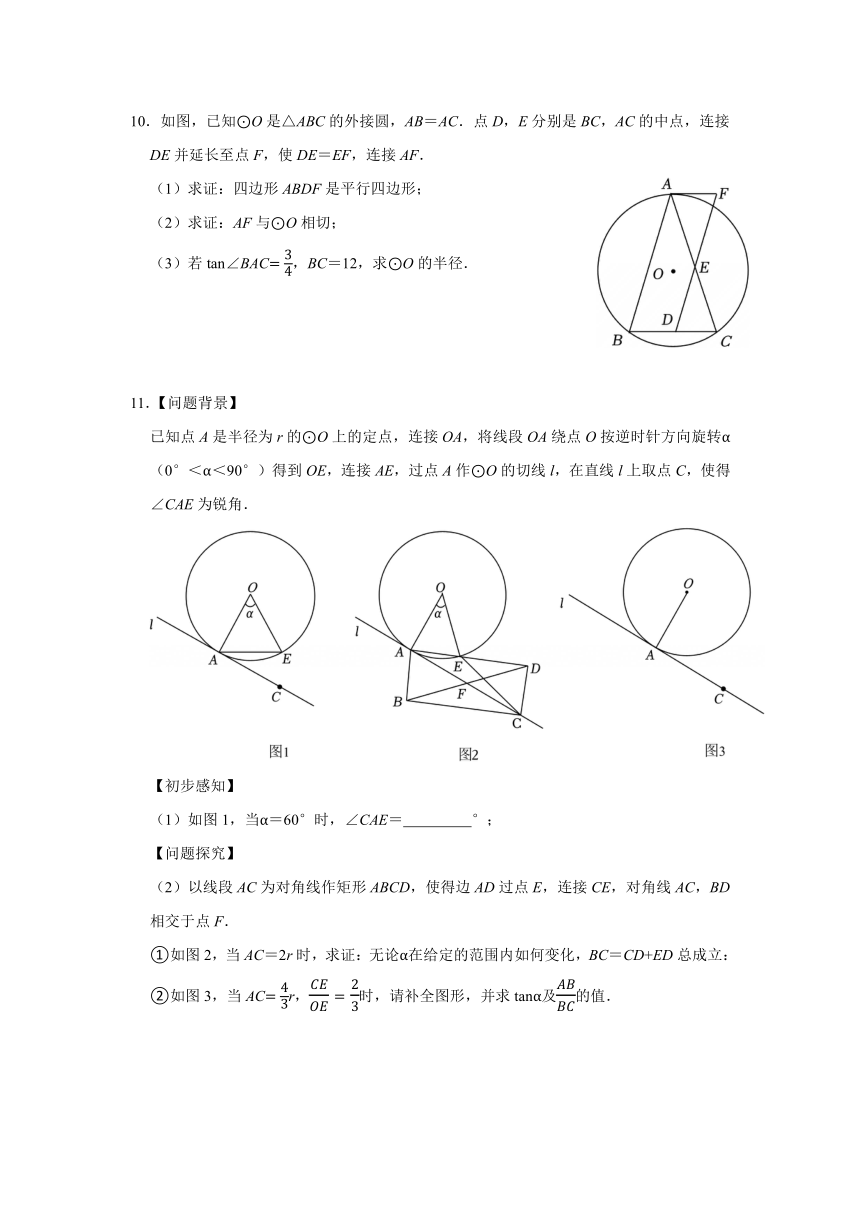
2.如图,AB是⊙O的直径,C,D是⊙O上两点,连接AC,BC,CO平分∠ACD,CE⊥DB,交DB延长线于点E.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为5,sinD,求BD的长.
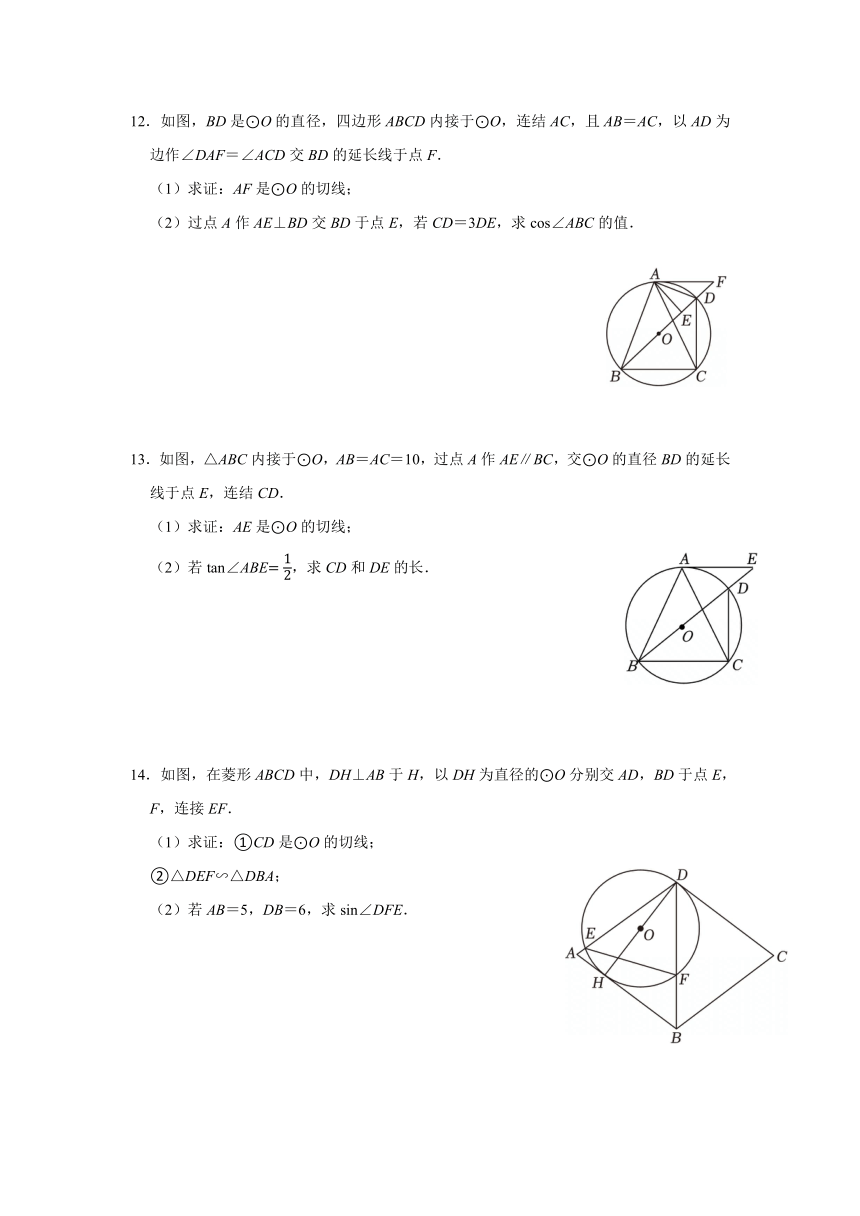
3.如图,在△ABC中,BA=BC,以AB为直径作⊙O交AC于点D,过点D作DE⊥BC,垂足为E,延长DE交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若BE=1,BF=3,求sinC的值.
4.如图,已知△ABC内接于⊙O,AB是⊙O的直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC,交AC的延长线于点E,连接BD,CD.
(1)求证:DE是⊙O的切线;
(2)若CE=1,,求⊙O的直径.
5.如图,△ABC内接于⊙O,AB为⊙O的直径,点D为⊙O上一点,BC=BD,延长BA至E,使得∠ADE=∠CBA.
(1)求证:ED是⊙O的切线;
(2)若BO=4,,求ED的长.
6.如图,在△ABC中,AC=BC,∠ACB=90°,⊙O经过A、C两点,交AB于点D,CO的延长线交AB于点F,DE∥CF交BC于点E.
(1)求证:DE为⊙O的切线;
(2)若AC=4,tan∠CFD=2,求⊙O的半径.
7.如图,△ABC中,∠ACB=90°,AC=BC,⊙O经过B,C两点,与斜边AB交于点E,连接CO并延长交AB于点M,交⊙O于点D,过点E作EF∥CD,交AC于点F.
(1)求证:EF是⊙O的切线;
(2)若BM=4,tan∠BCD,求OM的长.
8.如图,△ABC为等腰三角形,O是底边BC的中点,腰AC与半圆O相切于点D,底边BC与半圆O交于E,F两点.
(1)求证:AB与半圆O相切;
(2)连接OA.若CD=4,CF=2,求sin∠OAC的值.
9.如图,△ABC内接于⊙O,AB为⊙O的直径,CD⊥AB于点D,将△CDB沿BC所在的直线翻折,得到△CEB,点D的对应点为E,延长EC交BA的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若sin∠CFB,AB=8,求图中阴影部分的面积.
10.如图,已知⊙O是△ABC的外接圆,AB=AC.点D,E分别是BC,AC的中点,连接DE并延长至点F,使DE=EF,连接AF.
(1)求证:四边形ABDF是平行四边形;
(2)求证:AF与⊙O相切;
(3)若tan∠BAC,BC=12,求⊙O的半径.
11.【问题背景】
已知点A是半径为r的⊙O上的定点,连接OA,将线段OA绕点O按逆时针方向旋转α(0°<α<90°)得到OE,连接AE,过点A作⊙O的切线l,在直线l上取点C,使得∠CAE为锐角.
【初步感知】
(1)如图1,当α=60°时,∠CAE= °;
【问题探究】
(2)以线段AC为对角线作矩形ABCD,使得边AD过点E,连接CE,对角线AC,BD相交于点F.
①如图2,当AC=2r时,求证:无论α在给定的范围内如何变化,BC=CD+ED总成立:
②如图3,当ACr,时,请补全图形,并求tanα及的值.
12.如图,BD是⊙O的直径,四边形ABCD内接于⊙O,连结AC,且AB=AC,以AD为边作∠DAF=∠ACD交BD的延长线于点F.
(1)求证:AF是⊙O的切线;
(2)过点A作AE⊥BD交BD于点E,若CD=3DE,求cos∠ABC的值.
13.如图,△ABC内接于⊙O,AB=AC=10,过点A作AE∥BC,交⊙O的直径BD的延长线于点E,连结CD.
(1)求证:AE是⊙O的切线;
(2)若tan∠ABE,求CD和DE的长.
14.如图,在菱形ABCD中,DH⊥AB于H,以DH为直径的⊙O分别交AD,BD于点E,F,连接EF.
(1)求证:①CD是⊙O的切线;
②△DEF∽△DBA;
(2)若AB=5,DB=6,求sin∠DFE.
15.如图,AB是⊙O的直径,点C,E在⊙O上,∠CAB=2∠EAB,点F在线段AB的延长线上,且∠AFE=∠ABC.
(1)求证:EF与⊙O相切;
(2)若BF=1,sin∠AFE,求BC的长.
参考答案
1.【解答】解:(1)DE为⊙O的切线,理由为:
证明:连接OD,BD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=CB,
∴点D为AC的中点,
∵点O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∴∠ODE=∠DFC,
∵DE⊥BC,
∴∠DFC=90°,
∴∠ODE=90°,
∴DE⊥OD,
∵OD为⊙O的半径,D为OD的外端点,
∴DE为⊙O的切线;
(2)∵OD=OB,
∴∠ODB=∠OBD,
∵∠A+∠OBD=90°,∠BDE+∠ODB=90°,
∴∠A=∠BDE,即sinA=sin∠BDE,
在Rt△ABD中,∠ADB=90°,sinA,AB=18,
∴BD=ABsinA=186,
在Rt△BDF中,sin∠BDE,BD=6,
∴BF=BDsin∠BDE=62,
∵BF∥OD,
∴∠FBE=∠DOE,∠EFB=∠EDO,
∴△BEF∽△OED,
∴,即,
∴,
解得:BE.
2.【解答】(1)证明:∵OC=OA,
∴∠OCA=∠A,
∵CO平分∠ACD,
∴∠OCA=∠OCD,
∵∠A=∠D,
∴∠OCD=∠D,
∴OC∥DE,
∵CE⊥DB,交DB延长线于点E,
∴∠E=90°,
∴∠OCE=180°﹣∠E=90°,
∵OC是⊙O的半径,且CE⊥OC,
∴CE是⊙O的切线.
(2)解:∵⊙O的半径为5,AB是⊙O的直径,
∴AB=2×5=10,∠ACB=90°,
∵∠A=∠D,
∴sinA=sinD,
∴BCAB10=6,
∵OB=OC,
∴∠OCB=∠OBC,
∵∠BCE+∠OCB=∠OCE=90°,∠A+∠OBC=90°,
∴∠BCE=∠A,
∴sin∠BCE=sinA,
∴BEBC6,
∴CE,
∵AC8,
∴tanD=tanA,
∴DECE,
∴BD=DE﹣BE,
∴BD的长为.
3.【解答】(1)证明:连接OD,BD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=CB,
∴点D为AC的中点,
∵点O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∴∠ODE=∠DEC,
∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=90°,
∴DF⊥OD,
∵OD为⊙O的半径,D为OD的外端点,
∴DF为⊙O的切线;
(2)解:如上图,
∵DE⊥BC,BE=1,BF=3,
∴由勾股定理,得EF,
由(1)知BE∥OD,
∴△ODF∽△BEF,
∴,
∵BE=1,BF=3,OB=OD,
∴,
解得OB,DE,
∴AB=3,
在Rt△BDE中,
由勾股定理,得BD,
∵BA=BC,
∴∠C=∠A,
∴sinC=sinA.
4.【解答】(1)证明:连接OD,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠EAD,
∵DE⊥AE,
∴∠E=90°,
∴∠EAD+∠ADE=90°,
∴∠ODA+∠ADE=90°,
即∠ODE=90°,
∴OD⊥DE,
∵OD是⊙O半径,
∴DE是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
即∠DAB+∠ABC+∠DBC=90°,
∵∠EAD+∠ADE=90°,
∴∠EAD+∠ADC+∠CDE=90°,
∴∠DAB+∠ABC+∠DBC=∠EAD+∠ADC+∠CDE,
∵∠BAD=∠EAD,∠ABC=∠ADC,
∴∠DBC=∠CDE,
∵∠DBC=∠CAD,∠DCB=∠BAD,∠CAD=∠BAD,
∴∠CDE=∠DBC=∠DCB=∠BAD,
∴BD=CD,,
在Rt△CDE中,,
∴CD=3CE=3×1=3,
∴BD=3,
在Rt△ABD中,,
∴AB=3BD=3×3=9,
即⊙O的直径为9.
5.【解答】(1)证明:连接OD,如图所示:
∵AB为⊙O的直径,
∴∠BCA=∠BDA=90°,OB=OD,
∴∠DBA=∠BDO,
在Rt△BCA和Rt△BDA中,
,
∴Rt△BCA≌Rt△BDA(HL),
∴∠CBA=∠DBA,
∵∠ADE=∠CBA,∠DBA=∠BDO,
∴∠ADE=∠DBA=∠BDO,
∵∠BDO+∠ADO=∠BDA=90°,
∴∠ADE+∠ADO=90°,
即ED⊥OD,
∵OD为⊙O的半径,
∴ED是⊙O的切线;
(2)解:∵BO=4,
∴AB=2OB=8,
∴EB=AE+AB=AE+8,
∵tan∠CBA,∠CBA=∠DBA,
∴tan∠DBA,
在Rt△ABD中,tan∠DBA,
∴设AD=a,BD=2a,
∵∠ADE=∠DBA,∠E=∠E,
∴△EAD∽△EDB,
∴ED:EB=AE:ED=AD:BD,
即ED:(AE+8)=AE:ED=a:2a,
由AE:ED=a:2a,得:AEED,
由ED:(AE+8)=a:2a,得:2ED=AE+8,
∴2EDED+8,
∵ED.
6.【解答】(1)证明:连接OD,
∵AC=BC,∠ACB=90°,
∴△ACB为等腰直角三角形,
∴∠CAB=45°,
∴∠COD=2∠CAB=90°,
∵DE∥CF,
∴∠COD+∠EDO=180°,
∴∠EDO=90°
∴DE为⊙O的切线;
(2)解:过点C作CH⊥AB于点H,
∵△ACB为等腰直角三角形,AC=4,
∴CH=AH2,
∵tan∠CFD2,
∴FH,
在Rt△CFH中,由勾股定理得CF2=CH2+FH2,
∴,
∵tan∠CFD2,
∴OD.
故⊙O的半径为.
7.【解答】(1)证明:连接OE,
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∴∠COE=2∠ABC=90°,
∵EF∥CD,
∴∠COE+∠OEF=180°,
∴∠FEO=90°,
∵OE是⊙O的半径,
∴EF是⊙O的切线;
(2)解:过M作MH⊥BC于H,
则△BMH是等腰直角三角形,
∵BM=4,
∴BH=MHBM=4,
在Rt△CHM中,∵tan∠BCD,
∴CH=2MH=8,
∴CM4,CB=CH+BH=12,
连接BD,
∵CD是⊙O的直径,
∵BD⊥BC,
∴MH∥BD,
∴,
∴,
∴DM=2,
∴OD3,
∴OM=OD﹣DM.
8.【解答】(1)证明:连接OD,OA,作OH⊥AB于H,如图,
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO⊥BC,AO平分∠BAC,
∵AC与⊙O相切于点D,
∴OD⊥AC,
而OH⊥AB,
∴OH=OD,
∴AB是⊙O的切线;
(2)由(1)知OD⊥AC,
在Rt△OCD中,CD=4,OC=OF+CF=OD+2,OD2+CD2=OC2,
∴OD2+42=(OD+2)2,
∴OD=3,
∴OC=5,
∴cosC,
在Rt△OCA中,cosC,
∴sin∠OAC.
9.【解答】(1)证明:连接OC,
∵CD⊥AB,
∴∠BDC=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∵将△CDB沿BC所在的直线翻折,得到△CEB,
∴∠EBC=∠DBC,∠E=∠BDC=90°,
∴∠OCB=∠CBE,
∴OC∥BE,
∴∠OCF=∠E=90°,
∵OC是⊙O的半径,
∴CF是⊙O的切线;
(2)解:∵sin∠CFB,
∴∠CFB=45°,
∵∠COF=90°,
∴∠COF=∠CFO=45,
∴CF=OC4,
∴∠CDO=90°,
∴∠OCD=∠COD=45°,
∴CD=ODOC=2,
∴图中阴影部分的面积=扇形AOC的面积﹣△COD面积222π﹣4.
10.【解答】(1)证明:∵点D,E分别是BC,AC的中点,
∴BD=DC,AE=EC,
在△EDC和△EFA中,
,
∴△EDC≌△EFA(SAS),
∴DC=AF,∠EDC=∠F,
∴BC∥AF,BD=AF,
∴四边形ABDF是平行四边形;
(2)证明:连接AD,如图,
∵AB=AC,BD=DC
∴AD⊥BC,
∴AD垂直平分BC,
∴AD经过圆心O,
由(1)知:AF∥BC,
∴DA⊥AF,
∵OA为⊙O半径,
∴AF与⊙O相切;
(3)解:连接OB,OC,OD,如图,
∵OB=OC,BD=CDBC=6,
∴OD⊥BC,∠BOD∠BOC,
∵∠BAC∠BOC,
∴∠BOD=∠BAC.
∵tan∠BAC,
∴tan∠BOD,
∵tan∠BOD,
∴,
∴OD=8,
∴OB10,
∴⊙O的半径为10.
11.【解答】(1)解:∵α=60°,OA=OE,
∴∠OAE=∠OEA=α=60°,
∵AC与圆相切,
∴∠OAC=90°,
∴∠CAE=30°.
故答案为:30.
(2)证明:∵四边形ABCD是矩形,AC=2r,
∴OA=OE=CF=DF=r,
∵∠OAC=∠ADC=90°,
∴∠OAE+∠CAD=∠ACD+∠CAD,
∴∠OAE=∠ACD,
∵OA=OE,CF=DF,
∴∠OAE=∠OEA=∠ACD=∠CDF,
在△OAE和△FCD中,
,
∴△OAE≌△FCD(AAS),
∴AE=CD,
∵AD=AE+ED,
∴BC=CD+ED.
即无论α在给定的范围内如何变化,BC=CD+ED总成立.
(3)解:补全图形如图,
∵AC是切线,
∴∠OAC=90°,
∵AC,
∴tan∠AOC,
设OA=3m,则AC4m,OC=5m,
∵,OE=OA=3m,
∴CE=2m,OE+CE=5m=OC,
即点E在线段OC上,
∴tanα=tan∠AOC.
法一:如图,过O作OH⊥AE,垂足为H,则AH=EH,
∵∠OHE=90°=∠D,∠OEH=∠CED,
∴△OEH∽△CED,
∴,
设EH=AH=3a,则DE=2a,
∴AD=AH+EH+ED=8a,
在Rt△ACD中,CD2=AC2﹣AD2=16m2﹣64a2,
在Rt△CED中,CD2=CE2﹣ED2=4m2﹣4a2,
∴16m2﹣64a2=4m2﹣4a2,解得am,
∴BC=ADm,CDm=AB,
∴.
法二:由OH∥CD,得∠DCE=∠HOE=∠CAD,证△CAD∽△ECD,
直接得到,
∴.
12.【解答】(1)证明:如图所示,连接OA,
∵BD是⊙O的直径,
∴∠BAD=90°,
∴∠OAB+∠OAD=90°,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠DAF=∠ACD,∠OBA=∠ACD,
∴∠DAF=∠OAB,
∴∠DAF+∠OAD=∠OAB+∠OAD=90°,
∴∠OAF=90°,
∴OA⊥AF,
又∵OA是⊙O的半径,
∴AF是⊙O的切线;
(2)解:如图所示,延长CD交AF于H,延长AO交BC于G,连接OC,
∵BD是⊙O的直径,
∴∠BCD=90°,即CH⊥BC,
∵AB=AC,OB=OC,
∴OA垂直平分BC,
∴AG⊥BC,
∴AG∥CH,
又∵由(1)知AF与⊙O相切
∴∠OAF=90°
∴四边形AGCH为矩形
∴∠AHC=90°
∵AE⊥BD,
∴∠AEB=∠AHC=90°,
又∵∠ABE=∠ACH,
∴△ABE≌△ACH(AAS),
∴AE=AH,BE=CH,
∵AD=AD,
∴Rt△ADE≌Rt△ADH(HL),
∴DH=DE,设DH=DE=a,则CD=3a,
∴BE=CH=DH+CD=4a,
∴BD=BE+DE=5a,
∴OA=OD=2.5a,
∴OE=OD﹣DE=1.5a,
∴
∴,
∴,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ADE=∠ACB,
∴∠ABC=∠ADE,
∴.
13.【解答】(1)证明:连接并延长AO交BC于点F,连接OC,则OB=OC,
∵AB=AC,
∴∠AOB=∠AOC,
∴∠FOB=∠FOC,
∴OF⊥BC,
∵AE∥BC,
∴∠OAE=∠OFB=90°,
∵OA是⊙O的半径,且AE⊥OA,
∴AE是⊙O的切线.
(2)解:∵OB=OA,
∴∠BAF=∠ABE,
∴tan∠BAF=tan∠ABE,
∴AF=2BF,
∵ABBF=10,
∴BF=2,AF=4,
∵BF2+FO2=OB2,且OB=OA=4FO,
∴(2)2+FO2=(4FO)2,
解得FO,
∴OD=OB=OA=4,
∵OB=OD,BF=CF,
∴CD=2FO=23,
∵cos∠AOE=cos∠FOB,
∴OE,
∴DE=OE﹣OD,
∴CD的长是3,DE的长是.
14.【解答】(1)证明:①∵四边形ABCD是菱形,
∴AB∥CD,
∵DH⊥AB,
∴∠CDH=∠DHA=90°,
∴CD⊥OD,
∵D为⊙O的半径的外端点,
∴CD是⊙O的切线;
②连接HF,
∴∠DEF=∠DHF,
∵DH为⊙O直径,
∴∠DFH=90°,
∴∠DHF=90°﹣∠BDH,
∵∠DHB=90°,
∴∠DBA=90°﹣∠BDH,
∴∠DHF=∠DBA=∠DEF,
∵∠EDF=∠BDA,
∴△DEF∽△DBA;
(2)解:连接AC交BD于G.
∵菱形ABCD,BD=6,
∴AC⊥BD,AG=GC,DG=GB=3,
在Rt△AGB中,AG4,
∴AC=2AG=8,
∵S菱形ABCDAC BD=AB DH,
∴DH,
由△DEF∽△DBA知:∠DFE=∠DAH,
∴sin∠DFE=sin∠DAH.
15.【解答】(1)证明:如图,连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠FOE=∠OAE+∠OEA=2∠OAE,
∵∠CAB=2∠EAB,
∴∠CAB=∠FOE,
又∵∠AFE=∠ABC,
∴∠CAB+∠ABC=∠FOE+∠AFE,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°=∠FOE+∠AFE,
∴∠OEF=90°,
即OE⊥EF,
∵OE是半径,
∴EF是⊙O的切线;
(2)解:在Rt△EOF中,设半径为r,即OE=OB=r,则OF=r+1,
∵sin∠AFE,
∴r=4,
∴AB=2r=8,
在Rt△ABC中,sin∠ABCsin∠AFE,AB=8,
∴AC8,
∴BC.
1.如图,△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,交AB的延长线于点E,垂足为点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AB=18,,求BE的长.
2.如图,AB是⊙O的直径,C,D是⊙O上两点,连接AC,BC,CO平分∠ACD,CE⊥DB,交DB延长线于点E.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为5,sinD,求BD的长.
3.如图,在△ABC中,BA=BC,以AB为直径作⊙O交AC于点D,过点D作DE⊥BC,垂足为E,延长DE交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若BE=1,BF=3,求sinC的值.
4.如图,已知△ABC内接于⊙O,AB是⊙O的直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC,交AC的延长线于点E,连接BD,CD.
(1)求证:DE是⊙O的切线;
(2)若CE=1,,求⊙O的直径.
5.如图,△ABC内接于⊙O,AB为⊙O的直径,点D为⊙O上一点,BC=BD,延长BA至E,使得∠ADE=∠CBA.
(1)求证:ED是⊙O的切线;
(2)若BO=4,,求ED的长.
6.如图,在△ABC中,AC=BC,∠ACB=90°,⊙O经过A、C两点,交AB于点D,CO的延长线交AB于点F,DE∥CF交BC于点E.
(1)求证:DE为⊙O的切线;
(2)若AC=4,tan∠CFD=2,求⊙O的半径.
7.如图,△ABC中,∠ACB=90°,AC=BC,⊙O经过B,C两点,与斜边AB交于点E,连接CO并延长交AB于点M,交⊙O于点D,过点E作EF∥CD,交AC于点F.
(1)求证:EF是⊙O的切线;
(2)若BM=4,tan∠BCD,求OM的长.
8.如图,△ABC为等腰三角形,O是底边BC的中点,腰AC与半圆O相切于点D,底边BC与半圆O交于E,F两点.
(1)求证:AB与半圆O相切;
(2)连接OA.若CD=4,CF=2,求sin∠OAC的值.
9.如图,△ABC内接于⊙O,AB为⊙O的直径,CD⊥AB于点D,将△CDB沿BC所在的直线翻折,得到△CEB,点D的对应点为E,延长EC交BA的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若sin∠CFB,AB=8,求图中阴影部分的面积.
10.如图,已知⊙O是△ABC的外接圆,AB=AC.点D,E分别是BC,AC的中点,连接DE并延长至点F,使DE=EF,连接AF.
(1)求证:四边形ABDF是平行四边形;
(2)求证:AF与⊙O相切;
(3)若tan∠BAC,BC=12,求⊙O的半径.
11.【问题背景】
已知点A是半径为r的⊙O上的定点,连接OA,将线段OA绕点O按逆时针方向旋转α(0°<α<90°)得到OE,连接AE,过点A作⊙O的切线l,在直线l上取点C,使得∠CAE为锐角.
【初步感知】
(1)如图1,当α=60°时,∠CAE= °;
【问题探究】
(2)以线段AC为对角线作矩形ABCD,使得边AD过点E,连接CE,对角线AC,BD相交于点F.
①如图2,当AC=2r时,求证:无论α在给定的范围内如何变化,BC=CD+ED总成立:
②如图3,当ACr,时,请补全图形,并求tanα及的值.
12.如图,BD是⊙O的直径,四边形ABCD内接于⊙O,连结AC,且AB=AC,以AD为边作∠DAF=∠ACD交BD的延长线于点F.
(1)求证:AF是⊙O的切线;
(2)过点A作AE⊥BD交BD于点E,若CD=3DE,求cos∠ABC的值.
13.如图,△ABC内接于⊙O,AB=AC=10,过点A作AE∥BC,交⊙O的直径BD的延长线于点E,连结CD.
(1)求证:AE是⊙O的切线;
(2)若tan∠ABE,求CD和DE的长.
14.如图,在菱形ABCD中,DH⊥AB于H,以DH为直径的⊙O分别交AD,BD于点E,F,连接EF.
(1)求证:①CD是⊙O的切线;
②△DEF∽△DBA;
(2)若AB=5,DB=6,求sin∠DFE.
15.如图,AB是⊙O的直径,点C,E在⊙O上,∠CAB=2∠EAB,点F在线段AB的延长线上,且∠AFE=∠ABC.
(1)求证:EF与⊙O相切;
(2)若BF=1,sin∠AFE,求BC的长.
参考答案
1.【解答】解:(1)DE为⊙O的切线,理由为:
证明:连接OD,BD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=CB,
∴点D为AC的中点,
∵点O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∴∠ODE=∠DFC,
∵DE⊥BC,
∴∠DFC=90°,
∴∠ODE=90°,
∴DE⊥OD,
∵OD为⊙O的半径,D为OD的外端点,
∴DE为⊙O的切线;
(2)∵OD=OB,
∴∠ODB=∠OBD,
∵∠A+∠OBD=90°,∠BDE+∠ODB=90°,
∴∠A=∠BDE,即sinA=sin∠BDE,
在Rt△ABD中,∠ADB=90°,sinA,AB=18,
∴BD=ABsinA=186,
在Rt△BDF中,sin∠BDE,BD=6,
∴BF=BDsin∠BDE=62,
∵BF∥OD,
∴∠FBE=∠DOE,∠EFB=∠EDO,
∴△BEF∽△OED,
∴,即,
∴,
解得:BE.
2.【解答】(1)证明:∵OC=OA,
∴∠OCA=∠A,
∵CO平分∠ACD,
∴∠OCA=∠OCD,
∵∠A=∠D,
∴∠OCD=∠D,
∴OC∥DE,
∵CE⊥DB,交DB延长线于点E,
∴∠E=90°,
∴∠OCE=180°﹣∠E=90°,
∵OC是⊙O的半径,且CE⊥OC,
∴CE是⊙O的切线.
(2)解:∵⊙O的半径为5,AB是⊙O的直径,
∴AB=2×5=10,∠ACB=90°,
∵∠A=∠D,
∴sinA=sinD,
∴BCAB10=6,
∵OB=OC,
∴∠OCB=∠OBC,
∵∠BCE+∠OCB=∠OCE=90°,∠A+∠OBC=90°,
∴∠BCE=∠A,
∴sin∠BCE=sinA,
∴BEBC6,
∴CE,
∵AC8,
∴tanD=tanA,
∴DECE,
∴BD=DE﹣BE,
∴BD的长为.
3.【解答】(1)证明:连接OD,BD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=CB,
∴点D为AC的中点,
∵点O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∴∠ODE=∠DEC,
∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=90°,
∴DF⊥OD,
∵OD为⊙O的半径,D为OD的外端点,
∴DF为⊙O的切线;
(2)解:如上图,
∵DE⊥BC,BE=1,BF=3,
∴由勾股定理,得EF,
由(1)知BE∥OD,
∴△ODF∽△BEF,
∴,
∵BE=1,BF=3,OB=OD,
∴,
解得OB,DE,
∴AB=3,
在Rt△BDE中,
由勾股定理,得BD,
∵BA=BC,
∴∠C=∠A,
∴sinC=sinA.
4.【解答】(1)证明:连接OD,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠EAD,
∵DE⊥AE,
∴∠E=90°,
∴∠EAD+∠ADE=90°,
∴∠ODA+∠ADE=90°,
即∠ODE=90°,
∴OD⊥DE,
∵OD是⊙O半径,
∴DE是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
即∠DAB+∠ABC+∠DBC=90°,
∵∠EAD+∠ADE=90°,
∴∠EAD+∠ADC+∠CDE=90°,
∴∠DAB+∠ABC+∠DBC=∠EAD+∠ADC+∠CDE,
∵∠BAD=∠EAD,∠ABC=∠ADC,
∴∠DBC=∠CDE,
∵∠DBC=∠CAD,∠DCB=∠BAD,∠CAD=∠BAD,
∴∠CDE=∠DBC=∠DCB=∠BAD,
∴BD=CD,,
在Rt△CDE中,,
∴CD=3CE=3×1=3,
∴BD=3,
在Rt△ABD中,,
∴AB=3BD=3×3=9,
即⊙O的直径为9.
5.【解答】(1)证明:连接OD,如图所示:
∵AB为⊙O的直径,
∴∠BCA=∠BDA=90°,OB=OD,
∴∠DBA=∠BDO,
在Rt△BCA和Rt△BDA中,
,
∴Rt△BCA≌Rt△BDA(HL),
∴∠CBA=∠DBA,
∵∠ADE=∠CBA,∠DBA=∠BDO,
∴∠ADE=∠DBA=∠BDO,
∵∠BDO+∠ADO=∠BDA=90°,
∴∠ADE+∠ADO=90°,
即ED⊥OD,
∵OD为⊙O的半径,
∴ED是⊙O的切线;
(2)解:∵BO=4,
∴AB=2OB=8,
∴EB=AE+AB=AE+8,
∵tan∠CBA,∠CBA=∠DBA,
∴tan∠DBA,
在Rt△ABD中,tan∠DBA,
∴设AD=a,BD=2a,
∵∠ADE=∠DBA,∠E=∠E,
∴△EAD∽△EDB,
∴ED:EB=AE:ED=AD:BD,
即ED:(AE+8)=AE:ED=a:2a,
由AE:ED=a:2a,得:AEED,
由ED:(AE+8)=a:2a,得:2ED=AE+8,
∴2EDED+8,
∵ED.
6.【解答】(1)证明:连接OD,
∵AC=BC,∠ACB=90°,
∴△ACB为等腰直角三角形,
∴∠CAB=45°,
∴∠COD=2∠CAB=90°,
∵DE∥CF,
∴∠COD+∠EDO=180°,
∴∠EDO=90°
∴DE为⊙O的切线;
(2)解:过点C作CH⊥AB于点H,
∵△ACB为等腰直角三角形,AC=4,
∴CH=AH2,
∵tan∠CFD2,
∴FH,
在Rt△CFH中,由勾股定理得CF2=CH2+FH2,
∴,
∵tan∠CFD2,
∴OD.
故⊙O的半径为.
7.【解答】(1)证明:连接OE,
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∴∠COE=2∠ABC=90°,
∵EF∥CD,
∴∠COE+∠OEF=180°,
∴∠FEO=90°,
∵OE是⊙O的半径,
∴EF是⊙O的切线;
(2)解:过M作MH⊥BC于H,
则△BMH是等腰直角三角形,
∵BM=4,
∴BH=MHBM=4,
在Rt△CHM中,∵tan∠BCD,
∴CH=2MH=8,
∴CM4,CB=CH+BH=12,
连接BD,
∵CD是⊙O的直径,
∵BD⊥BC,
∴MH∥BD,
∴,
∴,
∴DM=2,
∴OD3,
∴OM=OD﹣DM.
8.【解答】(1)证明:连接OD,OA,作OH⊥AB于H,如图,
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO⊥BC,AO平分∠BAC,
∵AC与⊙O相切于点D,
∴OD⊥AC,
而OH⊥AB,
∴OH=OD,
∴AB是⊙O的切线;
(2)由(1)知OD⊥AC,
在Rt△OCD中,CD=4,OC=OF+CF=OD+2,OD2+CD2=OC2,
∴OD2+42=(OD+2)2,
∴OD=3,
∴OC=5,
∴cosC,
在Rt△OCA中,cosC,
∴sin∠OAC.
9.【解答】(1)证明:连接OC,
∵CD⊥AB,
∴∠BDC=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∵将△CDB沿BC所在的直线翻折,得到△CEB,
∴∠EBC=∠DBC,∠E=∠BDC=90°,
∴∠OCB=∠CBE,
∴OC∥BE,
∴∠OCF=∠E=90°,
∵OC是⊙O的半径,
∴CF是⊙O的切线;
(2)解:∵sin∠CFB,
∴∠CFB=45°,
∵∠COF=90°,
∴∠COF=∠CFO=45,
∴CF=OC4,
∴∠CDO=90°,
∴∠OCD=∠COD=45°,
∴CD=ODOC=2,
∴图中阴影部分的面积=扇形AOC的面积﹣△COD面积222π﹣4.
10.【解答】(1)证明:∵点D,E分别是BC,AC的中点,
∴BD=DC,AE=EC,
在△EDC和△EFA中,
,
∴△EDC≌△EFA(SAS),
∴DC=AF,∠EDC=∠F,
∴BC∥AF,BD=AF,
∴四边形ABDF是平行四边形;
(2)证明:连接AD,如图,
∵AB=AC,BD=DC
∴AD⊥BC,
∴AD垂直平分BC,
∴AD经过圆心O,
由(1)知:AF∥BC,
∴DA⊥AF,
∵OA为⊙O半径,
∴AF与⊙O相切;
(3)解:连接OB,OC,OD,如图,
∵OB=OC,BD=CDBC=6,
∴OD⊥BC,∠BOD∠BOC,
∵∠BAC∠BOC,
∴∠BOD=∠BAC.
∵tan∠BAC,
∴tan∠BOD,
∵tan∠BOD,
∴,
∴OD=8,
∴OB10,
∴⊙O的半径为10.
11.【解答】(1)解:∵α=60°,OA=OE,
∴∠OAE=∠OEA=α=60°,
∵AC与圆相切,
∴∠OAC=90°,
∴∠CAE=30°.
故答案为:30.
(2)证明:∵四边形ABCD是矩形,AC=2r,
∴OA=OE=CF=DF=r,
∵∠OAC=∠ADC=90°,
∴∠OAE+∠CAD=∠ACD+∠CAD,
∴∠OAE=∠ACD,
∵OA=OE,CF=DF,
∴∠OAE=∠OEA=∠ACD=∠CDF,
在△OAE和△FCD中,
,
∴△OAE≌△FCD(AAS),
∴AE=CD,
∵AD=AE+ED,
∴BC=CD+ED.
即无论α在给定的范围内如何变化,BC=CD+ED总成立.
(3)解:补全图形如图,
∵AC是切线,
∴∠OAC=90°,
∵AC,
∴tan∠AOC,
设OA=3m,则AC4m,OC=5m,
∵,OE=OA=3m,
∴CE=2m,OE+CE=5m=OC,
即点E在线段OC上,
∴tanα=tan∠AOC.
法一:如图,过O作OH⊥AE,垂足为H,则AH=EH,
∵∠OHE=90°=∠D,∠OEH=∠CED,
∴△OEH∽△CED,
∴,
设EH=AH=3a,则DE=2a,
∴AD=AH+EH+ED=8a,
在Rt△ACD中,CD2=AC2﹣AD2=16m2﹣64a2,
在Rt△CED中,CD2=CE2﹣ED2=4m2﹣4a2,
∴16m2﹣64a2=4m2﹣4a2,解得am,
∴BC=ADm,CDm=AB,
∴.
法二:由OH∥CD,得∠DCE=∠HOE=∠CAD,证△CAD∽△ECD,
直接得到,
∴.
12.【解答】(1)证明:如图所示,连接OA,
∵BD是⊙O的直径,
∴∠BAD=90°,
∴∠OAB+∠OAD=90°,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠DAF=∠ACD,∠OBA=∠ACD,
∴∠DAF=∠OAB,
∴∠DAF+∠OAD=∠OAB+∠OAD=90°,
∴∠OAF=90°,
∴OA⊥AF,
又∵OA是⊙O的半径,
∴AF是⊙O的切线;
(2)解:如图所示,延长CD交AF于H,延长AO交BC于G,连接OC,
∵BD是⊙O的直径,
∴∠BCD=90°,即CH⊥BC,
∵AB=AC,OB=OC,
∴OA垂直平分BC,
∴AG⊥BC,
∴AG∥CH,
又∵由(1)知AF与⊙O相切
∴∠OAF=90°
∴四边形AGCH为矩形
∴∠AHC=90°
∵AE⊥BD,
∴∠AEB=∠AHC=90°,
又∵∠ABE=∠ACH,
∴△ABE≌△ACH(AAS),
∴AE=AH,BE=CH,
∵AD=AD,
∴Rt△ADE≌Rt△ADH(HL),
∴DH=DE,设DH=DE=a,则CD=3a,
∴BE=CH=DH+CD=4a,
∴BD=BE+DE=5a,
∴OA=OD=2.5a,
∴OE=OD﹣DE=1.5a,
∴
∴,
∴,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ADE=∠ACB,
∴∠ABC=∠ADE,
∴.
13.【解答】(1)证明:连接并延长AO交BC于点F,连接OC,则OB=OC,
∵AB=AC,
∴∠AOB=∠AOC,
∴∠FOB=∠FOC,
∴OF⊥BC,
∵AE∥BC,
∴∠OAE=∠OFB=90°,
∵OA是⊙O的半径,且AE⊥OA,
∴AE是⊙O的切线.
(2)解:∵OB=OA,
∴∠BAF=∠ABE,
∴tan∠BAF=tan∠ABE,
∴AF=2BF,
∵ABBF=10,
∴BF=2,AF=4,
∵BF2+FO2=OB2,且OB=OA=4FO,
∴(2)2+FO2=(4FO)2,
解得FO,
∴OD=OB=OA=4,
∵OB=OD,BF=CF,
∴CD=2FO=23,
∵cos∠AOE=cos∠FOB,
∴OE,
∴DE=OE﹣OD,
∴CD的长是3,DE的长是.
14.【解答】(1)证明:①∵四边形ABCD是菱形,
∴AB∥CD,
∵DH⊥AB,
∴∠CDH=∠DHA=90°,
∴CD⊥OD,
∵D为⊙O的半径的外端点,
∴CD是⊙O的切线;
②连接HF,
∴∠DEF=∠DHF,
∵DH为⊙O直径,
∴∠DFH=90°,
∴∠DHF=90°﹣∠BDH,
∵∠DHB=90°,
∴∠DBA=90°﹣∠BDH,
∴∠DHF=∠DBA=∠DEF,
∵∠EDF=∠BDA,
∴△DEF∽△DBA;
(2)解:连接AC交BD于G.
∵菱形ABCD,BD=6,
∴AC⊥BD,AG=GC,DG=GB=3,
在Rt△AGB中,AG4,
∴AC=2AG=8,
∵S菱形ABCDAC BD=AB DH,
∴DH,
由△DEF∽△DBA知:∠DFE=∠DAH,
∴sin∠DFE=sin∠DAH.
15.【解答】(1)证明:如图,连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠FOE=∠OAE+∠OEA=2∠OAE,
∵∠CAB=2∠EAB,
∴∠CAB=∠FOE,
又∵∠AFE=∠ABC,
∴∠CAB+∠ABC=∠FOE+∠AFE,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°=∠FOE+∠AFE,
∴∠OEF=90°,
即OE⊥EF,
∵OE是半径,
∴EF是⊙O的切线;
(2)解:在Rt△EOF中,设半径为r,即OE=OB=r,则OF=r+1,
∵sin∠AFE,
∴r=4,
∴AB=2r=8,
在Rt△ABC中,sin∠ABCsin∠AFE,AB=8,
∴AC8,
∴BC.
同课章节目录
