北师大版2024—2025学年七年级下册数学期中考试模拟考试试卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下册数学期中考试模拟考试试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 615.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 12:34:04 | ||
图片预览



文档简介
北师大版2024—2025学年七年级下册数学期中考试模拟考试试卷春季
一、选择题
1.世界上几乎所有的生物都是由细胞组成的,科学家发现,一个细胞的平均质量约为0.00000000011毫克.用科学记数法表示0.00000000011正确的是( )
A.1.1×10﹣9 B.1.1×10﹣10 C.11×10﹣11 D.1.1×1010
2.下列长度的三根小木棒,不能摆成三角形的是( )
A.6cm,6cm,13cm B.5cm,7cm,11cm
C.9cm,6cm,8cm D.3cm,4cm,5cm
3.如图,直线l∥AB,D为直线l上一点,∠1=58°,CE为∠ACD的角平分线,交直线l于点E,则∠ACE=( )
A.29° B.51° C.61° D.122°
4.如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.AB=DC B.∠CBE=∠BCE C.AC=DB D.∠A=∠D
5.如图,CM是△ABC的中线,BC=8cm,若△BCM的周长比△ACM的周长大2cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
6.如图所示,在△ABC中,已知点D、E、F分别是BC、AD、CE的中点,且△ABC的面积为64,则△BEF的面积是( )
A.18 B.16
C.14 D.12
7.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
A.SAS B.SSS C.ASA D.AAS
8.如图,小李用若干长方体小木块,分别垒了两堵与地面垂直的木块墙,其中木块墙AD=24cm,CE=12cm.木块墙之间刚好可以放进一个等腰直角三角板,点B在DE上,点A和C分别与木块墙的顶端重合,则两堵木块墙之间的距离DE为( )
A.48cm B.42cm
C.38cm D.36cm
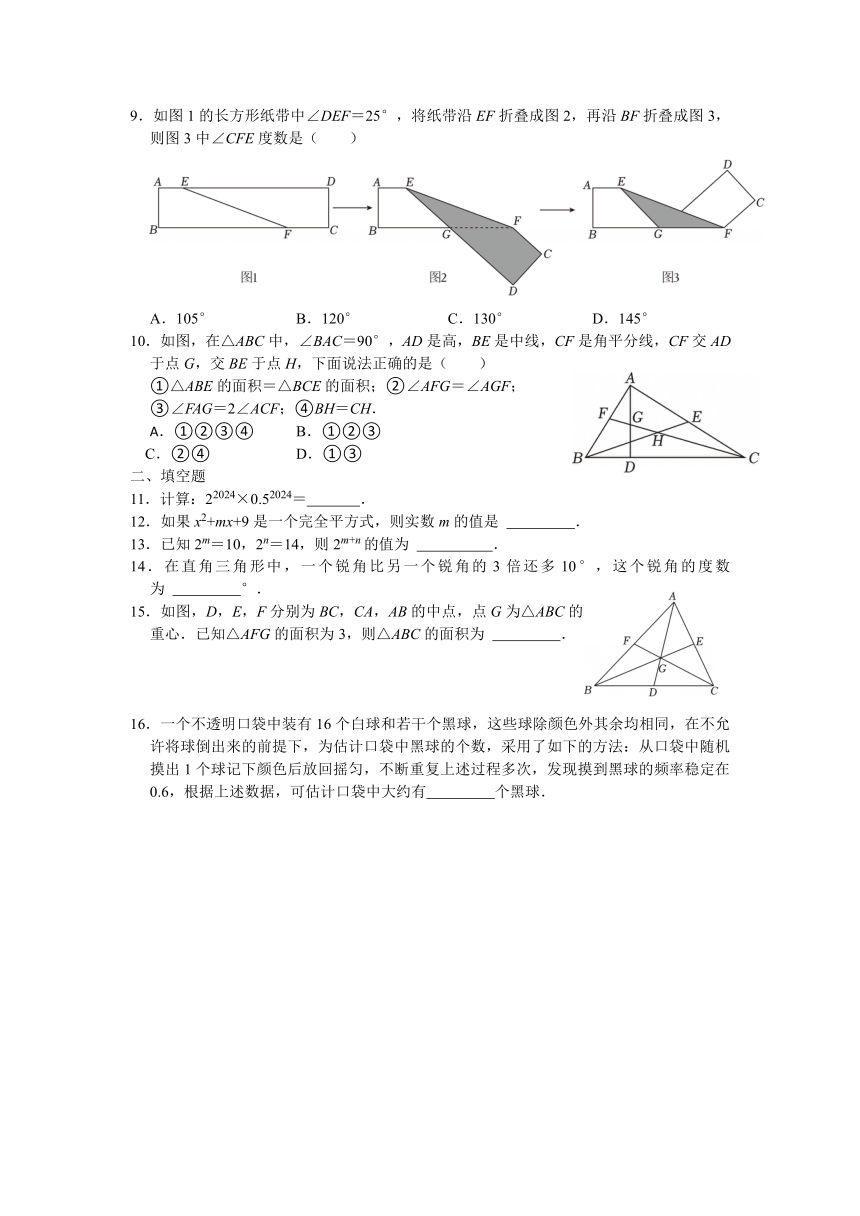
9.如图1的长方形纸带中∠DEF=25°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是( )
A.105° B.120° C.130° D.145°
10.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;
③∠FAG=2∠ACF;④BH=CH.
①②③④ B.①②③
C.②④ D.①③
二、填空题
11.计算:22024×0.52024= .
12.如果x2+mx+9是一个完全平方式,则实数m的值是 .
13.已知2m=10,2n=14,则2m+n的值为 .
14.在直角三角形中,一个锐角比另一个锐角的3倍还多10°,这个锐角的度数为 °.
15.如图,D,E,F分别为BC,CA,AB的中点,点G为△ABC的重心.已知△AFG的面积为3,则△ABC的面积为 .
16.一个不透明口袋中装有16个白球和若干个黑球,这些球除颜色外其余均相同,在不允许将球倒出来的前提下,为估计口袋中黑球的个数,采用了如下的方法:从口袋中随机摸出1个球记下颜色后放回摇匀,不断重复上述过程多次,发现摸到黑球的频率稳定在0.6,根据上述数据,可估计口袋中大约有 个黑球.
北师大版2024—2025学年七年级下册数学期中考试模拟考试试卷春季
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
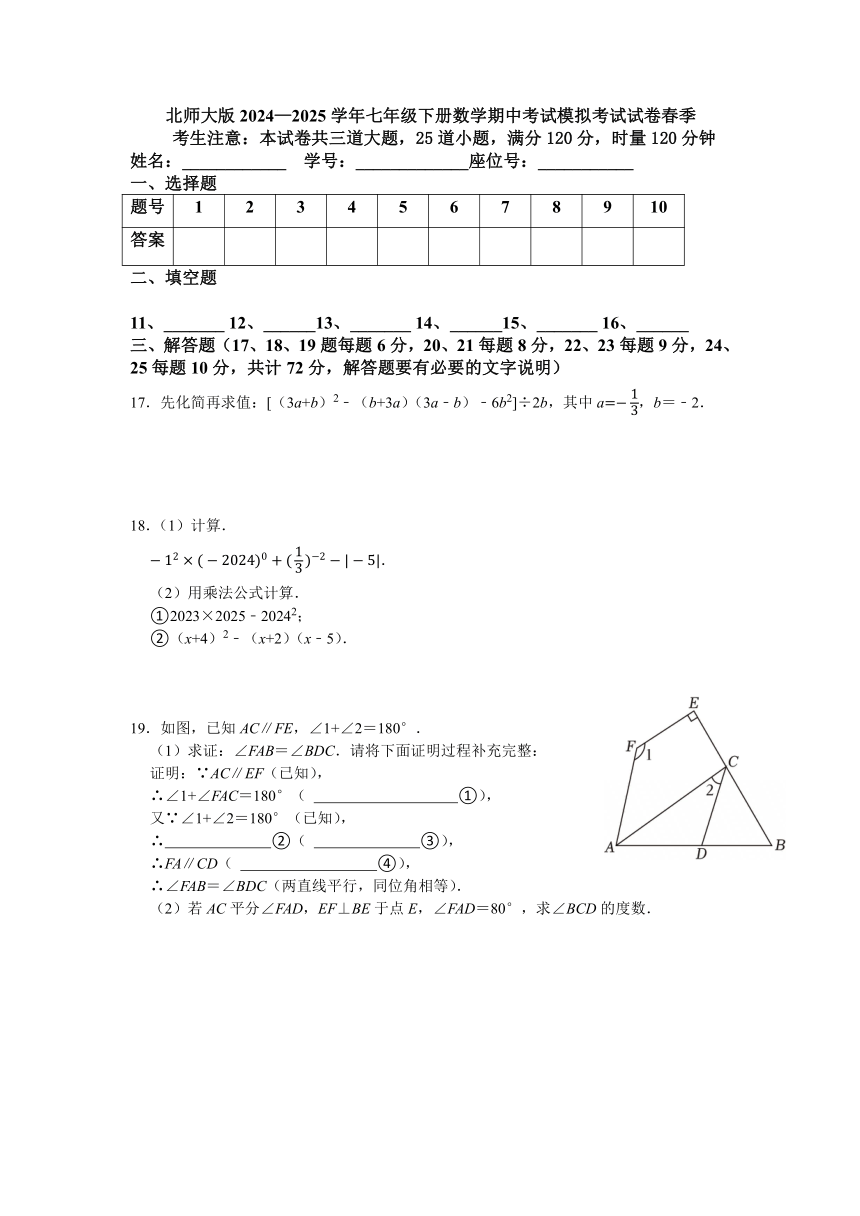
17.先化简再求值:[(3a+b)2﹣(b+3a)(3a﹣b)﹣6b2]÷2b,其中a,b=﹣2.
18.(1)计算.
.
(2)用乘法公式计算.
①2023×2025﹣20242;
②(x+4)2﹣(x+2)(x﹣5).
19.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC.请将下面证明过程补充完整:
证明:∵AC∥EF(已知),
∴∠1+∠FAC=180°( ①),
又∵∠1+∠2=180°(已知),
∴ ②( ③),
∴FA∥CD( ④),
∴∠FAB=∠BDC(两直线平行,同位角相等).
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
20.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
21.已知:如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,CD与BE相交于点F.
(1)求证:△ADC≌△FDB.
(2)若BD=12,AC=13,求AD的长.
22.如图是某学校操场一角,在长为(3a+5b)米,宽为(4a﹣b)米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为b米.
(1)求这两个篮球场的占地面积;
(2)若篮球场每平方米造价为200元,其余场地每平方米造价50元,求整个长方形场地的造价.
23.已知直线PQ∥MN,点C在直线PQ上,点B是平面内一点,连接BC交直线MN于点H,过点B作BA⊥BC交直线MN于点A.
(1)若点B在直线MN的右侧,
①如图1,已知∠BCQ=65°,求∠BAM的度数;
②如图2,过点B作BD⊥MN于点D,请判断∠ABD与∠BCQ是否相等,并说明理由;
(2)如图3,若点B在直线PQ和MN之间,过点B作BD⊥MN于点D,在点E,F直线MN上,BE,BF分别是∠ABD,∠CBD的角平分线.若∠ABF=3∠ABE,求∠EBC的度数.
24.将完全平方公式:(a±b)2=a2±2ab+b2进行适当的变形,可以解决很多的数学问题.如:a2+b2=(a+b)2﹣2ab,a2+b2=(a﹣b)2+2ab.
【阅读材料】
已知(3﹣x)(x﹣1)=﹣5,求(3﹣x)2+(x﹣1)2的值.
解:设3﹣x=a,x﹣1=b,则(3﹣x)(x﹣1)=ab=﹣5,a+b=3﹣x+x﹣1=2,
∵a2+b2=(a+b)2﹣2ab
∴(3﹣x)2+(x﹣1)2=a2+b2=22﹣2×(﹣5)=14.
【类比探究】请仿照材料中的方法,解决下列问题:
(1)若x+y=6,x2+y2=30,求xy的值;
(2)已知(4﹣x)(5﹣x)=8,求(4﹣x)2+(5﹣x)2的值;
【问题解决】
(3)如图,长方形APIE和长方形HQCF的长和宽分别为a,b(a<6,b<6),将它们放置在边长为6的正方形ABCD中,若长方形的周长为16,面积为15.75,求图中阴影部分面积S1+S2+S3.
25.我们定义:如果两个多项式M与N的和为常数,则称M与N互为“对消多项式”,这个常数称为它们的“对消值”.如MF=2x2﹣x+6与N=﹣2x2+x﹣1互为“对消多项式”,它们的“对消值”为5.
(1)下列各组多项式互为“对消多项式”的是 (填序号):
①3x2+2x与3x2+2;
②x﹣6与﹣x+2;
③﹣5x2y3+2xy与5x2y3﹣2xy﹣1.
(2)多项式A=(x﹣a)2与多项式B=﹣bx2﹣2x+b(a,b为常数)互为“对消多项式”,求它们的“对消值”;
(3)关于x的多项式C=mx2+6x+4与D=﹣m(x+1)(x+n)互为“对消多项式”,“对消值”为t.若a﹣b=m,b﹣c=mn,求代数式a2+b2+c2﹣ab﹣bc﹣ac+2t的最小值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C C D B B D A B
二、填空题
11.【解答】解:22024×0.52024=(2×0.5)2024=1,
故答案为:1.
12.【解答】解:∵x2+mx+9是一个完全平方式,x2+mx+9=x2+mx+32,
∴mx=±2x 3,
解得m=±6.
故答案为:±6.
13.【解答】解:原式=2m 2n=10×14=140,
故答案为:140.
14.【解答】解:设较小锐角的度数是x,则较大锐角的度数是(3x+10),
∴x+3x+10=90,
解得x=20.
∴3x+10=70,
∴较大锐角为70°,
故答案为:70.
15.【解答】解:∵△AFG的面积为3,D,E,F分别为BC,CA,AB的中点,
∴S△AFG=S△BFG=3,S△AEG=S△CEG,,
∴S△BFG=S△CEG=3,
∴S△BFG=S△AFG=S△AEG=S△CEG=3,
同理S△BDG=S△CDG=3
∴△ABC的面积为3×6=18,
故答案为:18.
16.【解答】解:摸到黑球的频率稳定在0.6,即摸到黑球的概率为0.6,
设口袋中有16个白球和x个黑球,
根据题意,得,
解得x=24,
经检验,x=24是原方程的解,
估计口袋中大约有24个黑球.
故答案为:24.
三、解答题
17.【解答】解:[(3a+b)2﹣(b+3a)(3a﹣b)﹣6b2]÷2b
=(9a2+b2+6ab﹣3ab+b2﹣9a2+3ab﹣6b2)÷2b
=(﹣4b2+6ab)÷2b
=﹣2b+3a,
当a,b=﹣2时,原式=﹣2×(﹣2)+3×()=3.
18.【解答】解:(1)
=﹣1×1+9﹣5
=﹣1+9﹣5
=3;
(2)①2023×2025﹣20242
=(2024﹣1)×(2024+1)﹣20242
=20242﹣1﹣20242
=﹣1;
②(x+4)2﹣(x+2)(x﹣5)
=x2+8x+16﹣(x2﹣3x﹣10)
=x2+8x+16﹣x2+3x+10
=11x+26.
19.【解答】(1)证明:∵AC∥EF(已知),
∴∠1+∠FAC=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠FAC=∠2(等角的补角相等),
∴FA∥CD(内错角相等,两直线平行),
∴∠FAB=∠BDC(两直线平行,同位角相等),
故答案为:两直线平行,同旁内角互补;∠FAC=∠2;等角的补角相等;内错角相等,两直线平行;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2∠FAD,
∵∠FAD=80°,
∴∠280°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
20.【解答】解:(1)a=59÷100=0.59,b=200×0.58=116.
故答案为:0.59,116
(2)“摸到白球的”的概率的估计值是0.6;
故答案为:0.6
(3)12÷0.6﹣12=8(个).
答:除白球外,还有大约8个其它颜色的小球;
21.【解答】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠FDB=90°,∠A+∠DBF=∠A+∠ACD=90°,
即∠DBF=∠ACD,
∵∠ABC=45°,CD⊥AB,
∴∠BCD=∠ABC=45°,
∴DB=DC,
在△ADC和△FDB中,
,
∴△ADC≌△FDB(ASA);
(2)解:∵△ADC≌△FDB,
∴AD=DF,AC=BF=13,
在Rt△FDB中,BD=12,
∴DF5,
∴AD=5.
22.【解答】解:(1)(3a+5b﹣3b)(4a﹣b﹣2b)
=(3a+2b)(4a﹣3b)
=(12a2﹣ab﹣6b2)平方米.
故这两个篮球场的占地面积是(12a2﹣ab﹣6b2)平方米;
(2)(3a+5b)(4a﹣b)=(12a2+17ab﹣5b2)平方米,
(12a2+17ab﹣5b2)﹣(12a2﹣ab﹣6b2)
=12a2+17ab﹣5b2﹣12a2+ab+6b2
=(18ab+b2)平方米,
200(12a2﹣ab﹣6b2)+50(18ab+b2)
=2400a2﹣200ab﹣1200b2+900ab+50b2
=(2400a2+700ab﹣1150b2)元.
故整个长方形场地的造价(2400a2+700ab﹣1150b2)元.
23.【解答】解:(1)①∵PQ∥MN,
∴∠BHA=∠BCQ=65°,
∵BA⊥BC,即∠CBA=90°,
∴∠BAM=25°;
②∠ABD=∠BCQ,
∵PQ∥MN,
∴∠BHA=∠BCQ,
∵BA⊥BC,即∠CBA=90°,
∴∠BHA+∠BAM=90°,
∵BD⊥MN,即∠BDN=90°,
∴∠ABD+∠BAM=90°,
∴∠ABD=∠BHA,
∴∠ABD=∠BCQ;
(2)∵BE,BF分别是∠ABD,∠CBD的角平分线,
∴∠ABE=∠EBD,∠CBF=∠DBF,
∵∠ABF=3∠ABE,即∠ABE∠ABF,
∴∠EBD∠ABF,
∴∠CBF=∠DBF=∠EBD+∠ABE+∠ABF∠ABF,
∵BA⊥BC,
∴∠ABF+∠CBF=90°,即∠ABF=90°,
解得:∠ABF°,
∴∠ABE°,∠CBF°,
∴∠EBC=∠CBF+∠ABF+∠ABE=()°.
24.【解答】解:(1)∵(x+y)2=x2+2xy+y2,x+y=6,x2+y2=30,
∴62=30+2xy,
∴xy=3;
(2)设4﹣x=a,5﹣x=b,则(4﹣x)(5﹣x)=ab=8,a﹣b=4﹣x﹣5+x=﹣1,
∵a2+b2=(a﹣b)2+2ab
∴(4﹣x)2+(5﹣x)2=a2+b2=(﹣1)2+2×8=17;
(3)∵长方形的周长为16,面积为15.75,
∴a+b=16÷2=8,ab=15.75,
∴S1+S2+S3
=(6﹣a)2+(a+b﹣6)2+(6﹣b)2
=[(6﹣a)+(6﹣b)]2﹣2(6﹣a)(6﹣b)+(a+b﹣6)2
=[12﹣(a+b)]2﹣2(6﹣a)(6﹣b)+(a+b﹣6)2
=[12﹣(a+b)]2﹣2[36﹣6(a+b)+ab]+(a+b﹣6)2
=(12﹣8)2﹣2×(36﹣6×8+15.75)+(8﹣6)2
=16﹣7.5+4
=12.5.
25.【解答】解:(1)∵3x2+2x+3x2+2=6x2+2x+2,
x﹣6﹣x+2=﹣4,
﹣5x2y3+2xy+5x2y3﹣2xy﹣1=﹣1,
∴①组多项式不是互为“对消多项式”,
②③组多项式是互为“对消多项式”,
故答案为:②③;
(2)∵A=(x﹣a)2=x2﹣2ax+a2,B=﹣bx2﹣2x+b,
∴A+B
=x2﹣2ax+a2﹣bx2﹣2x+b
=(1﹣b)x2+(﹣2a﹣2)x+(a2+b),
∵A与B互为“对消多项式”,
∴1﹣b=0,﹣2a﹣2=0,
解得a=﹣1,b=1.
∴a2+b
=(﹣1)2+1
=1+1
=2,
∴它们的“对消值”是2;
(3)∵C=mx2+6x+4,D=﹣m(x+1)(x+n)=﹣mx2+(﹣mn﹣m)x﹣mn,
∴C+D=(6﹣mn﹣m)x+(4﹣mn),
∵C与D互为“对消多项式”且“对消值”为t,
∵a﹣b=m,b﹣c=mn,
∴a﹣c=(a﹣b)+(b﹣c)=m+mn=6,
∴a2+b2+c2﹣ab﹣bc﹣ac+2t
=m2﹣4m+32
=(m﹣2)2+28≥28,
∴代数式 a2+b2+c2=ab=bc=ac+2 的最小值是28.
一、选择题
1.世界上几乎所有的生物都是由细胞组成的,科学家发现,一个细胞的平均质量约为0.00000000011毫克.用科学记数法表示0.00000000011正确的是( )
A.1.1×10﹣9 B.1.1×10﹣10 C.11×10﹣11 D.1.1×1010
2.下列长度的三根小木棒,不能摆成三角形的是( )
A.6cm,6cm,13cm B.5cm,7cm,11cm
C.9cm,6cm,8cm D.3cm,4cm,5cm
3.如图,直线l∥AB,D为直线l上一点,∠1=58°,CE为∠ACD的角平分线,交直线l于点E,则∠ACE=( )
A.29° B.51° C.61° D.122°
4.如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.AB=DC B.∠CBE=∠BCE C.AC=DB D.∠A=∠D
5.如图,CM是△ABC的中线,BC=8cm,若△BCM的周长比△ACM的周长大2cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
6.如图所示,在△ABC中,已知点D、E、F分别是BC、AD、CE的中点,且△ABC的面积为64,则△BEF的面积是( )
A.18 B.16
C.14 D.12
7.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
A.SAS B.SSS C.ASA D.AAS
8.如图,小李用若干长方体小木块,分别垒了两堵与地面垂直的木块墙,其中木块墙AD=24cm,CE=12cm.木块墙之间刚好可以放进一个等腰直角三角板,点B在DE上,点A和C分别与木块墙的顶端重合,则两堵木块墙之间的距离DE为( )
A.48cm B.42cm
C.38cm D.36cm
9.如图1的长方形纸带中∠DEF=25°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是( )
A.105° B.120° C.130° D.145°
10.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;
③∠FAG=2∠ACF;④BH=CH.
①②③④ B.①②③
C.②④ D.①③
二、填空题
11.计算:22024×0.52024= .
12.如果x2+mx+9是一个完全平方式,则实数m的值是 .
13.已知2m=10,2n=14,则2m+n的值为 .
14.在直角三角形中,一个锐角比另一个锐角的3倍还多10°,这个锐角的度数为 °.
15.如图,D,E,F分别为BC,CA,AB的中点,点G为△ABC的重心.已知△AFG的面积为3,则△ABC的面积为 .
16.一个不透明口袋中装有16个白球和若干个黑球,这些球除颜色外其余均相同,在不允许将球倒出来的前提下,为估计口袋中黑球的个数,采用了如下的方法:从口袋中随机摸出1个球记下颜色后放回摇匀,不断重复上述过程多次,发现摸到黑球的频率稳定在0.6,根据上述数据,可估计口袋中大约有 个黑球.
北师大版2024—2025学年七年级下册数学期中考试模拟考试试卷春季
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简再求值:[(3a+b)2﹣(b+3a)(3a﹣b)﹣6b2]÷2b,其中a,b=﹣2.
18.(1)计算.
.
(2)用乘法公式计算.
①2023×2025﹣20242;
②(x+4)2﹣(x+2)(x﹣5).
19.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC.请将下面证明过程补充完整:
证明:∵AC∥EF(已知),
∴∠1+∠FAC=180°( ①),
又∵∠1+∠2=180°(已知),
∴ ②( ③),
∴FA∥CD( ④),
∴∠FAB=∠BDC(两直线平行,同位角相等).
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
20.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 59 96 b 295 480 601
摸到白球的频率 a 0.64 0.58 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
21.已知:如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,CD与BE相交于点F.
(1)求证:△ADC≌△FDB.
(2)若BD=12,AC=13,求AD的长.
22.如图是某学校操场一角,在长为(3a+5b)米,宽为(4a﹣b)米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为b米.
(1)求这两个篮球场的占地面积;
(2)若篮球场每平方米造价为200元,其余场地每平方米造价50元,求整个长方形场地的造价.
23.已知直线PQ∥MN,点C在直线PQ上,点B是平面内一点,连接BC交直线MN于点H,过点B作BA⊥BC交直线MN于点A.
(1)若点B在直线MN的右侧,
①如图1,已知∠BCQ=65°,求∠BAM的度数;
②如图2,过点B作BD⊥MN于点D,请判断∠ABD与∠BCQ是否相等,并说明理由;
(2)如图3,若点B在直线PQ和MN之间,过点B作BD⊥MN于点D,在点E,F直线MN上,BE,BF分别是∠ABD,∠CBD的角平分线.若∠ABF=3∠ABE,求∠EBC的度数.
24.将完全平方公式:(a±b)2=a2±2ab+b2进行适当的变形,可以解决很多的数学问题.如:a2+b2=(a+b)2﹣2ab,a2+b2=(a﹣b)2+2ab.
【阅读材料】
已知(3﹣x)(x﹣1)=﹣5,求(3﹣x)2+(x﹣1)2的值.
解:设3﹣x=a,x﹣1=b,则(3﹣x)(x﹣1)=ab=﹣5,a+b=3﹣x+x﹣1=2,
∵a2+b2=(a+b)2﹣2ab
∴(3﹣x)2+(x﹣1)2=a2+b2=22﹣2×(﹣5)=14.
【类比探究】请仿照材料中的方法,解决下列问题:
(1)若x+y=6,x2+y2=30,求xy的值;
(2)已知(4﹣x)(5﹣x)=8,求(4﹣x)2+(5﹣x)2的值;
【问题解决】
(3)如图,长方形APIE和长方形HQCF的长和宽分别为a,b(a<6,b<6),将它们放置在边长为6的正方形ABCD中,若长方形的周长为16,面积为15.75,求图中阴影部分面积S1+S2+S3.
25.我们定义:如果两个多项式M与N的和为常数,则称M与N互为“对消多项式”,这个常数称为它们的“对消值”.如MF=2x2﹣x+6与N=﹣2x2+x﹣1互为“对消多项式”,它们的“对消值”为5.
(1)下列各组多项式互为“对消多项式”的是 (填序号):
①3x2+2x与3x2+2;
②x﹣6与﹣x+2;
③﹣5x2y3+2xy与5x2y3﹣2xy﹣1.
(2)多项式A=(x﹣a)2与多项式B=﹣bx2﹣2x+b(a,b为常数)互为“对消多项式”,求它们的“对消值”;
(3)关于x的多项式C=mx2+6x+4与D=﹣m(x+1)(x+n)互为“对消多项式”,“对消值”为t.若a﹣b=m,b﹣c=mn,求代数式a2+b2+c2﹣ab﹣bc﹣ac+2t的最小值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C C D B B D A B
二、填空题
11.【解答】解:22024×0.52024=(2×0.5)2024=1,
故答案为:1.
12.【解答】解:∵x2+mx+9是一个完全平方式,x2+mx+9=x2+mx+32,
∴mx=±2x 3,
解得m=±6.
故答案为:±6.
13.【解答】解:原式=2m 2n=10×14=140,
故答案为:140.
14.【解答】解:设较小锐角的度数是x,则较大锐角的度数是(3x+10),
∴x+3x+10=90,
解得x=20.
∴3x+10=70,
∴较大锐角为70°,
故答案为:70.
15.【解答】解:∵△AFG的面积为3,D,E,F分别为BC,CA,AB的中点,
∴S△AFG=S△BFG=3,S△AEG=S△CEG,,
∴S△BFG=S△CEG=3,
∴S△BFG=S△AFG=S△AEG=S△CEG=3,
同理S△BDG=S△CDG=3
∴△ABC的面积为3×6=18,
故答案为:18.
16.【解答】解:摸到黑球的频率稳定在0.6,即摸到黑球的概率为0.6,
设口袋中有16个白球和x个黑球,
根据题意,得,
解得x=24,
经检验,x=24是原方程的解,
估计口袋中大约有24个黑球.
故答案为:24.
三、解答题
17.【解答】解:[(3a+b)2﹣(b+3a)(3a﹣b)﹣6b2]÷2b
=(9a2+b2+6ab﹣3ab+b2﹣9a2+3ab﹣6b2)÷2b
=(﹣4b2+6ab)÷2b
=﹣2b+3a,
当a,b=﹣2时,原式=﹣2×(﹣2)+3×()=3.
18.【解答】解:(1)
=﹣1×1+9﹣5
=﹣1+9﹣5
=3;
(2)①2023×2025﹣20242
=(2024﹣1)×(2024+1)﹣20242
=20242﹣1﹣20242
=﹣1;
②(x+4)2﹣(x+2)(x﹣5)
=x2+8x+16﹣(x2﹣3x﹣10)
=x2+8x+16﹣x2+3x+10
=11x+26.
19.【解答】(1)证明:∵AC∥EF(已知),
∴∠1+∠FAC=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠FAC=∠2(等角的补角相等),
∴FA∥CD(内错角相等,两直线平行),
∴∠FAB=∠BDC(两直线平行,同位角相等),
故答案为:两直线平行,同旁内角互补;∠FAC=∠2;等角的补角相等;内错角相等,两直线平行;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2∠FAD,
∵∠FAD=80°,
∴∠280°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
20.【解答】解:(1)a=59÷100=0.59,b=200×0.58=116.
故答案为:0.59,116
(2)“摸到白球的”的概率的估计值是0.6;
故答案为:0.6
(3)12÷0.6﹣12=8(个).
答:除白球外,还有大约8个其它颜色的小球;
21.【解答】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠FDB=90°,∠A+∠DBF=∠A+∠ACD=90°,
即∠DBF=∠ACD,
∵∠ABC=45°,CD⊥AB,
∴∠BCD=∠ABC=45°,
∴DB=DC,
在△ADC和△FDB中,
,
∴△ADC≌△FDB(ASA);
(2)解:∵△ADC≌△FDB,
∴AD=DF,AC=BF=13,
在Rt△FDB中,BD=12,
∴DF5,
∴AD=5.
22.【解答】解:(1)(3a+5b﹣3b)(4a﹣b﹣2b)
=(3a+2b)(4a﹣3b)
=(12a2﹣ab﹣6b2)平方米.
故这两个篮球场的占地面积是(12a2﹣ab﹣6b2)平方米;
(2)(3a+5b)(4a﹣b)=(12a2+17ab﹣5b2)平方米,
(12a2+17ab﹣5b2)﹣(12a2﹣ab﹣6b2)
=12a2+17ab﹣5b2﹣12a2+ab+6b2
=(18ab+b2)平方米,
200(12a2﹣ab﹣6b2)+50(18ab+b2)
=2400a2﹣200ab﹣1200b2+900ab+50b2
=(2400a2+700ab﹣1150b2)元.
故整个长方形场地的造价(2400a2+700ab﹣1150b2)元.
23.【解答】解:(1)①∵PQ∥MN,
∴∠BHA=∠BCQ=65°,
∵BA⊥BC,即∠CBA=90°,
∴∠BAM=25°;
②∠ABD=∠BCQ,
∵PQ∥MN,
∴∠BHA=∠BCQ,
∵BA⊥BC,即∠CBA=90°,
∴∠BHA+∠BAM=90°,
∵BD⊥MN,即∠BDN=90°,
∴∠ABD+∠BAM=90°,
∴∠ABD=∠BHA,
∴∠ABD=∠BCQ;
(2)∵BE,BF分别是∠ABD,∠CBD的角平分线,
∴∠ABE=∠EBD,∠CBF=∠DBF,
∵∠ABF=3∠ABE,即∠ABE∠ABF,
∴∠EBD∠ABF,
∴∠CBF=∠DBF=∠EBD+∠ABE+∠ABF∠ABF,
∵BA⊥BC,
∴∠ABF+∠CBF=90°,即∠ABF=90°,
解得:∠ABF°,
∴∠ABE°,∠CBF°,
∴∠EBC=∠CBF+∠ABF+∠ABE=()°.
24.【解答】解:(1)∵(x+y)2=x2+2xy+y2,x+y=6,x2+y2=30,
∴62=30+2xy,
∴xy=3;
(2)设4﹣x=a,5﹣x=b,则(4﹣x)(5﹣x)=ab=8,a﹣b=4﹣x﹣5+x=﹣1,
∵a2+b2=(a﹣b)2+2ab
∴(4﹣x)2+(5﹣x)2=a2+b2=(﹣1)2+2×8=17;
(3)∵长方形的周长为16,面积为15.75,
∴a+b=16÷2=8,ab=15.75,
∴S1+S2+S3
=(6﹣a)2+(a+b﹣6)2+(6﹣b)2
=[(6﹣a)+(6﹣b)]2﹣2(6﹣a)(6﹣b)+(a+b﹣6)2
=[12﹣(a+b)]2﹣2(6﹣a)(6﹣b)+(a+b﹣6)2
=[12﹣(a+b)]2﹣2[36﹣6(a+b)+ab]+(a+b﹣6)2
=(12﹣8)2﹣2×(36﹣6×8+15.75)+(8﹣6)2
=16﹣7.5+4
=12.5.
25.【解答】解:(1)∵3x2+2x+3x2+2=6x2+2x+2,
x﹣6﹣x+2=﹣4,
﹣5x2y3+2xy+5x2y3﹣2xy﹣1=﹣1,
∴①组多项式不是互为“对消多项式”,
②③组多项式是互为“对消多项式”,
故答案为:②③;
(2)∵A=(x﹣a)2=x2﹣2ax+a2,B=﹣bx2﹣2x+b,
∴A+B
=x2﹣2ax+a2﹣bx2﹣2x+b
=(1﹣b)x2+(﹣2a﹣2)x+(a2+b),
∵A与B互为“对消多项式”,
∴1﹣b=0,﹣2a﹣2=0,
解得a=﹣1,b=1.
∴a2+b
=(﹣1)2+1
=1+1
=2,
∴它们的“对消值”是2;
(3)∵C=mx2+6x+4,D=﹣m(x+1)(x+n)=﹣mx2+(﹣mn﹣m)x﹣mn,
∴C+D=(6﹣mn﹣m)x+(4﹣mn),
∵C与D互为“对消多项式”且“对消值”为t,
∵a﹣b=m,b﹣c=mn,
∴a﹣c=(a﹣b)+(b﹣c)=m+mn=6,
∴a2+b2+c2﹣ab﹣bc﹣ac+2t
=m2﹣4m+32
=(m﹣2)2+28≥28,
∴代数式 a2+b2+c2=ab=bc=ac+2 的最小值是28.
同课章节目录
