2025年中考数学一轮复习 小测验1 实数及其运算(含详解)
文档属性
| 名称 | 2025年中考数学一轮复习 小测验1 实数及其运算(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 560.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 14:46:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1 实数及其运算
分值:50分 时间30分钟
选择题(15分)
1.(2024·广东·模拟预测)某市2024年1月的最高气温为,最低气温为零下,则计算2024年1月该市温差列式正确的是( )
A. B.
C. D.
2.(2024·湖南·模拟预测)我国是最早使用负数的国家,在数据,,0,,,中是负数的有( )
A.1个 B.2个 C.3个 D.4个
3.(2024·山西·模拟预测)2023年11月15日,部署在塔里木盆地的中国石化“深地一号”跃进井测试获得高产油气流,日产原油200吨,天然气5万立方米.以此计算,该油井天然气年(按365天)产量用科学记数法表示( )
A.立方米 B.立方米
C.立方米 D.立方米
4.(2024·新疆乌鲁木齐·三模)比2024的倒数小的数是( )
A.1 B.2024 C. D.
5.(2024·北京·中考真题)实数,在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
填空题(15分)
6.(2024·湖南·中考真题)计算: .
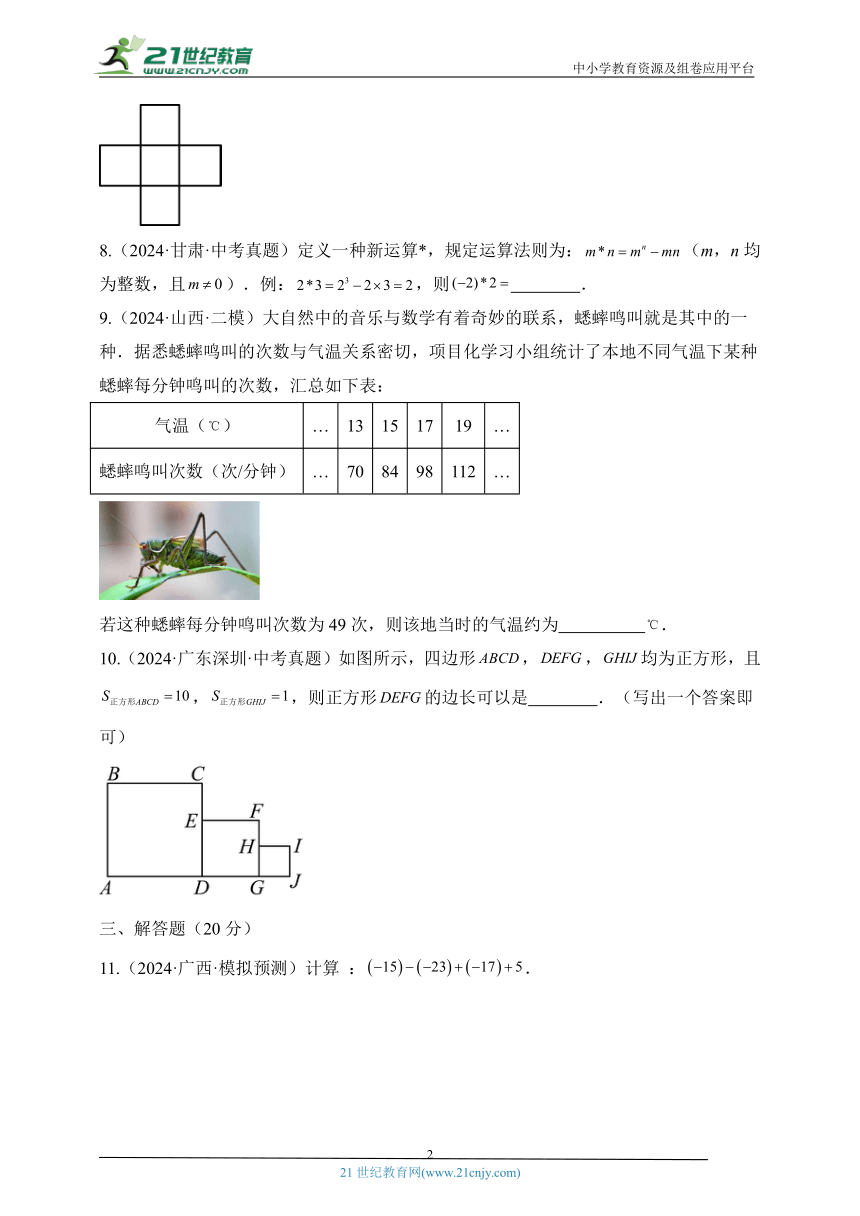
7.(2024·陕西·中考真题)小华探究“幻方”时,提出了一个问题:如图,将0,,,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 .(写出一个符合题意的数即可)
8.(2024·甘肃·中考真题)定义一种新运算*,规定运算法则为:(m,n均为整数,且).例:,则 .
9.(2024·山西·二模)大自然中的音乐与数学有着奇妙的联系,蟋蟀鸣叫就是其中的一种.据悉蟋蟀鸣叫的次数与气温关系密切,项目化学习小组统计了本地不同气温下某种蟋蟀每分钟鸣叫的次数,汇总如下表:
气温() … 13 15 17 19 …
蟋蟀鸣叫次数(次/分钟) … 70 84 98 112 …
若这种蟋蟀每分钟鸣叫次数为49次,则该地当时的气温约为 .
10.(2024·广东深圳·中考真题)如图所示,四边形,,均为正方形,且,,则正方形的边长可以是 .(写出一个答案即可)
解答题(20分)
11.(2024·广西·模拟预测)计算 :.
12.(2024·西藏·中考真题)计算:.
13.为积极倡导“阳光体育”运动,某班派6名同学参加“一分钟跳绳”比赛,负责记录成绩的嘉嘉以160次为标准,超出的次数记为正数,不足的次数记为负数,其中5名同学的成绩记录(单位:次)为:﹣10,+4,+11,﹣9,+1.
(1)求这5名同学的最好成绩与最差成绩相差多少次?
(2)若这6名同学的平均成绩超过了160次,求剩下的那名同学的成绩最少为多少.
14.在数学活动课上,李老师设计了一个游戏活动,四名同学分别代表一种运算,四名同学可以任意排列,每次排列代表一种运算顺序,剩余同学中,一名学生负责说一个数,其他同学负责运算,运算结果既对又快者获胜,可以得到一个奖品.
下面我们用四个卡片代表四名同学(如图):
(1)列式,并计算:
①﹣3经过A,B,C,D的顺序运算后,结果是多少?
②5经过B,C,A,D的顺序运算后,结果是多少?
(2)探究:数a经过D,C,A,B的顺序运算后,结果是45,a是多少?
答案版
一、选择题(15分)
1.(2024·广东·模拟预测)某市2024年1月的最高气温为,最低气温为零下,则计算2024年1月该市温差列式正确的是( )
A. B.
C. D.
【答案】A
【详解】解:∵某市2024年1月的最高气温为,最低气温为零下,
∴2024年1月该市温差为,
故选:A.
2.(2024·湖南·模拟预测)我国是最早使用负数的国家,在数据,,0,,,中是负数的有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【详解】解:,是负数,共2个,
故选:B.
3.(2024·山西·模拟预测)2023年11月15日,部署在塔里木盆地的中国石化“深地一号”跃进井测试获得高产油气流,日产原油200吨,天然气5万立方米.以此计算,该油井天然气年(按365天)产量用科学记数法表示( )
A.立方米 B.立方米
C.立方米 D.立方米
【答案】B
【详解】(立方米).
故选:B.
4.(2024·新疆乌鲁木齐·三模)比2024的倒数小的数是( )
A.1 B.2024 C. D.
【答案】D
【详解】解:2024的倒数是,
∵,
∴比2024的倒数小的数是,
故选D
5.(2024·北京·中考真题)实数,在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
【答案】C
【详解】解:A、由数轴可知,故本选项不符合题意;
B、由数轴可知,由绝对值的意义知,故本选项不符合题意;
C、由数轴可知,而,则,故,故本选项符合题意;
D、由数轴可知,而,因此,故本选项不符合题意.
故选:C.
二、填空题(15分)
6.(2024·湖南·中考真题)计算: .
【答案】2024
【详解】解:,
故答案为:2024.
7.(2024·陕西·中考真题)小华探究“幻方”时,提出了一个问题:如图,将0,,,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 .(写出一个符合题意的数即可)
【答案】0
【详解】解:由题意,填写如下:
,满足题意;
故答案为:0.
8.(2024·甘肃·中考真题)定义一种新运算*,规定运算法则为:(m,n均为整数,且).例:,则 .
【答案】8
【详解】根据定义,得,
故答案为:8.
9.(2024·山西·二模)大自然中的音乐与数学有着奇妙的联系,蟋蟀鸣叫就是其中的一种.据悉蟋蟀鸣叫的次数与气温关系密切,项目化学习小组统计了本地不同气温下某种蟋蟀每分钟鸣叫的次数,汇总如下表:
气温() … 13 15 17 19 …
蟋蟀鸣叫次数(次/分钟) … 70 84 98 112 …
若这种蟋蟀每分钟鸣叫次数为49次,则该地当时的气温约为 .
【答案】10
【详解】解:有表格数据可知,温度每升高,蟋蟀每分钟鸣叫的次数增加14次,
由此,在温度为时,蟋蟀每分钟鸣叫的70次的基础上可得,
,
即这种蟋蟀每分钟鸣叫次数为49次,则该地当时的气温约为.
故答案为:10.
10.(2024·广东深圳·中考真题)如图所示,四边形,,均为正方形,且,,则正方形的边长可以是 .(写出一个答案即可)
【答案】2(答案不唯一)
【详解】解:∵,
∴,
∵,
∴,
∵,即,
∴正方形的边长,即,
∴正方形的边长可以是2,
故答案为:2(答案不唯一).
三、解答题(20分)
11.(2024·广西·模拟预测)计算 :.
【答案】
【详解】解:原式
.
12.(2024·西藏·中考真题)计算:.
【答案】
【详解】解:
.
13.为积极倡导“阳光体育”运动,某班派6名同学参加“一分钟跳绳”比赛,负责记录成绩的嘉嘉以160次为标准,超出的次数记为正数,不足的次数记为负数,其中5名同学的成绩记录(单位:次)为:﹣10,+4,+11,﹣9,+1.
(1)求这5名同学的最好成绩与最差成绩相差多少次?
(2)若这6名同学的平均成绩超过了160次,求剩下的那名同学的成绩最少为多少.
【解答】解:(1)+11﹣(﹣10)
=11+10
=21(次),
答:这5名同学的最好成绩与最差成绩相差21次.
(2)设剩下的那名同学的成绩可记为a,
由题意可得﹣10+4+11﹣9+1+a>0,解得a>3,
∴剩下的那名同学的成绩最少为160+4=164(次).
答:剩下的那名同学的成绩最少为164次.
14.在数学活动课上,李老师设计了一个游戏活动,四名同学分别代表一种运算,四名同学可以任意排列,每次排列代表一种运算顺序,剩余同学中,一名学生负责说一个数,其他同学负责运算,运算结果既对又快者获胜,可以得到一个奖品.
下面我们用四个卡片代表四名同学(如图):
(1)列式,并计算:
①﹣3经过A,B,C,D的顺序运算后,结果是多少?
②5经过B,C,A,D的顺序运算后,结果是多少?
(2)探究:数a经过D,C,A,B的顺序运算后,结果是45,a是多少?
【解答】解:(1)①[(﹣3)×2﹣(﹣5)]2+6
=(﹣6+5)2+6
=(﹣1)2+6
=1+6
=7;
②[5﹣(﹣5)]2×2+6
=(5+5)2×2+6
=102×2+6
=100×2+6
=200+6
=206;
(2)由题意知,(a+6)2×2﹣(﹣5)=45,
∴(a+6)2×2=40,
∴(a+6)2=20,
∴a+6=±2,
∴a1=26,a2=﹣26.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1 实数及其运算
分值:50分 时间30分钟
选择题(15分)
1.(2024·广东·模拟预测)某市2024年1月的最高气温为,最低气温为零下,则计算2024年1月该市温差列式正确的是( )
A. B.
C. D.
2.(2024·湖南·模拟预测)我国是最早使用负数的国家,在数据,,0,,,中是负数的有( )
A.1个 B.2个 C.3个 D.4个
3.(2024·山西·模拟预测)2023年11月15日,部署在塔里木盆地的中国石化“深地一号”跃进井测试获得高产油气流,日产原油200吨,天然气5万立方米.以此计算,该油井天然气年(按365天)产量用科学记数法表示( )
A.立方米 B.立方米
C.立方米 D.立方米
4.(2024·新疆乌鲁木齐·三模)比2024的倒数小的数是( )
A.1 B.2024 C. D.
5.(2024·北京·中考真题)实数,在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
填空题(15分)
6.(2024·湖南·中考真题)计算: .
7.(2024·陕西·中考真题)小华探究“幻方”时,提出了一个问题:如图,将0,,,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 .(写出一个符合题意的数即可)
8.(2024·甘肃·中考真题)定义一种新运算*,规定运算法则为:(m,n均为整数,且).例:,则 .
9.(2024·山西·二模)大自然中的音乐与数学有着奇妙的联系,蟋蟀鸣叫就是其中的一种.据悉蟋蟀鸣叫的次数与气温关系密切,项目化学习小组统计了本地不同气温下某种蟋蟀每分钟鸣叫的次数,汇总如下表:
气温() … 13 15 17 19 …
蟋蟀鸣叫次数(次/分钟) … 70 84 98 112 …
若这种蟋蟀每分钟鸣叫次数为49次,则该地当时的气温约为 .
10.(2024·广东深圳·中考真题)如图所示,四边形,,均为正方形,且,,则正方形的边长可以是 .(写出一个答案即可)
解答题(20分)
11.(2024·广西·模拟预测)计算 :.
12.(2024·西藏·中考真题)计算:.
13.为积极倡导“阳光体育”运动,某班派6名同学参加“一分钟跳绳”比赛,负责记录成绩的嘉嘉以160次为标准,超出的次数记为正数,不足的次数记为负数,其中5名同学的成绩记录(单位:次)为:﹣10,+4,+11,﹣9,+1.
(1)求这5名同学的最好成绩与最差成绩相差多少次?
(2)若这6名同学的平均成绩超过了160次,求剩下的那名同学的成绩最少为多少.
14.在数学活动课上,李老师设计了一个游戏活动,四名同学分别代表一种运算,四名同学可以任意排列,每次排列代表一种运算顺序,剩余同学中,一名学生负责说一个数,其他同学负责运算,运算结果既对又快者获胜,可以得到一个奖品.
下面我们用四个卡片代表四名同学(如图):
(1)列式,并计算:
①﹣3经过A,B,C,D的顺序运算后,结果是多少?
②5经过B,C,A,D的顺序运算后,结果是多少?
(2)探究:数a经过D,C,A,B的顺序运算后,结果是45,a是多少?
答案版
一、选择题(15分)
1.(2024·广东·模拟预测)某市2024年1月的最高气温为,最低气温为零下,则计算2024年1月该市温差列式正确的是( )
A. B.
C. D.
【答案】A
【详解】解:∵某市2024年1月的最高气温为,最低气温为零下,
∴2024年1月该市温差为,
故选:A.
2.(2024·湖南·模拟预测)我国是最早使用负数的国家,在数据,,0,,,中是负数的有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【详解】解:,是负数,共2个,
故选:B.
3.(2024·山西·模拟预测)2023年11月15日,部署在塔里木盆地的中国石化“深地一号”跃进井测试获得高产油气流,日产原油200吨,天然气5万立方米.以此计算,该油井天然气年(按365天)产量用科学记数法表示( )
A.立方米 B.立方米
C.立方米 D.立方米
【答案】B
【详解】(立方米).
故选:B.
4.(2024·新疆乌鲁木齐·三模)比2024的倒数小的数是( )
A.1 B.2024 C. D.
【答案】D
【详解】解:2024的倒数是,
∵,
∴比2024的倒数小的数是,
故选D
5.(2024·北京·中考真题)实数,在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
【答案】C
【详解】解:A、由数轴可知,故本选项不符合题意;
B、由数轴可知,由绝对值的意义知,故本选项不符合题意;
C、由数轴可知,而,则,故,故本选项符合题意;
D、由数轴可知,而,因此,故本选项不符合题意.
故选:C.
二、填空题(15分)
6.(2024·湖南·中考真题)计算: .
【答案】2024
【详解】解:,
故答案为:2024.
7.(2024·陕西·中考真题)小华探究“幻方”时,提出了一个问题:如图,将0,,,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 .(写出一个符合题意的数即可)
【答案】0
【详解】解:由题意,填写如下:
,满足题意;
故答案为:0.
8.(2024·甘肃·中考真题)定义一种新运算*,规定运算法则为:(m,n均为整数,且).例:,则 .
【答案】8
【详解】根据定义,得,
故答案为:8.
9.(2024·山西·二模)大自然中的音乐与数学有着奇妙的联系,蟋蟀鸣叫就是其中的一种.据悉蟋蟀鸣叫的次数与气温关系密切,项目化学习小组统计了本地不同气温下某种蟋蟀每分钟鸣叫的次数,汇总如下表:
气温() … 13 15 17 19 …
蟋蟀鸣叫次数(次/分钟) … 70 84 98 112 …
若这种蟋蟀每分钟鸣叫次数为49次,则该地当时的气温约为 .
【答案】10
【详解】解:有表格数据可知,温度每升高,蟋蟀每分钟鸣叫的次数增加14次,
由此,在温度为时,蟋蟀每分钟鸣叫的70次的基础上可得,
,
即这种蟋蟀每分钟鸣叫次数为49次,则该地当时的气温约为.
故答案为:10.
10.(2024·广东深圳·中考真题)如图所示,四边形,,均为正方形,且,,则正方形的边长可以是 .(写出一个答案即可)
【答案】2(答案不唯一)
【详解】解:∵,
∴,
∵,
∴,
∵,即,
∴正方形的边长,即,
∴正方形的边长可以是2,
故答案为:2(答案不唯一).
三、解答题(20分)
11.(2024·广西·模拟预测)计算 :.
【答案】
【详解】解:原式
.
12.(2024·西藏·中考真题)计算:.
【答案】
【详解】解:
.
13.为积极倡导“阳光体育”运动,某班派6名同学参加“一分钟跳绳”比赛,负责记录成绩的嘉嘉以160次为标准,超出的次数记为正数,不足的次数记为负数,其中5名同学的成绩记录(单位:次)为:﹣10,+4,+11,﹣9,+1.
(1)求这5名同学的最好成绩与最差成绩相差多少次?
(2)若这6名同学的平均成绩超过了160次,求剩下的那名同学的成绩最少为多少.
【解答】解:(1)+11﹣(﹣10)
=11+10
=21(次),
答:这5名同学的最好成绩与最差成绩相差21次.
(2)设剩下的那名同学的成绩可记为a,
由题意可得﹣10+4+11﹣9+1+a>0,解得a>3,
∴剩下的那名同学的成绩最少为160+4=164(次).
答:剩下的那名同学的成绩最少为164次.
14.在数学活动课上,李老师设计了一个游戏活动,四名同学分别代表一种运算,四名同学可以任意排列,每次排列代表一种运算顺序,剩余同学中,一名学生负责说一个数,其他同学负责运算,运算结果既对又快者获胜,可以得到一个奖品.
下面我们用四个卡片代表四名同学(如图):
(1)列式,并计算:
①﹣3经过A,B,C,D的顺序运算后,结果是多少?
②5经过B,C,A,D的顺序运算后,结果是多少?
(2)探究:数a经过D,C,A,B的顺序运算后,结果是45,a是多少?
【解答】解:(1)①[(﹣3)×2﹣(﹣5)]2+6
=(﹣6+5)2+6
=(﹣1)2+6
=1+6
=7;
②[5﹣(﹣5)]2×2+6
=(5+5)2×2+6
=102×2+6
=100×2+6
=200+6
=206;
(2)由题意知,(a+6)2×2﹣(﹣5)=45,
∴(a+6)2×2=40,
∴(a+6)2=20,
∴a+6=±2,
∴a1=26,a2=﹣26.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
