锐角三角函数(复习课)课件
图片预览






文档简介
课件20张PPT。锐角三角函数复习课
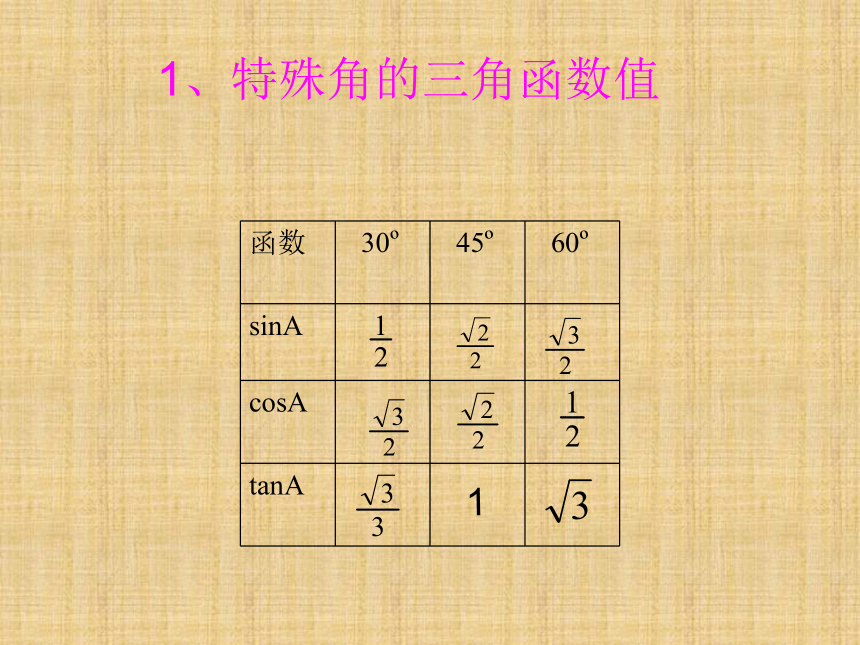
1、特殊角的三角函数值12、在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c 、a、b ,其中除直角c 外,
其余的5个元素之间有以下的关系: ⑴ 三边之间的关系( )⑵ 锐角之间的关系( )⑶ 边角之间的关系:知识拓展如图:在直角三角形ABC中,
sinA= ( ) =cosB
sinB= ( ) =( )
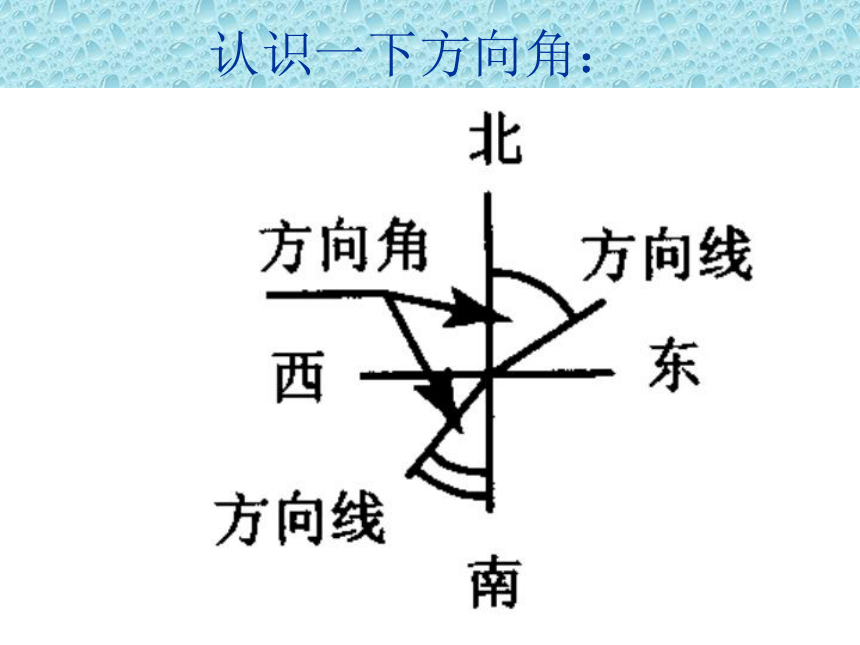
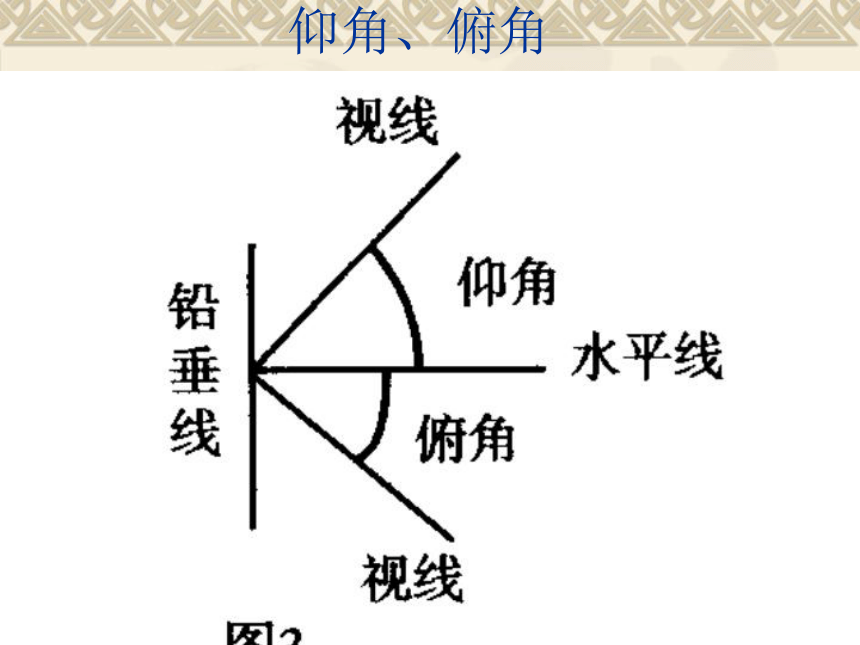
cosA这是互为余角之间的函数关系认识一下方向角:仰角、俯角1、锐角A满足2sin(A-15o )= ,则 A=( )您能行75o解:∵2sin(A-15)o=
∴sin(A-15)o=
∴A-15o=60o 即 A=75o体验成功2、在△ABC,∠A, ∠B均为锐角,且∣tanB- |
+(2sinA- )2=0,则△ABC是( )三角形。
A 等腰 B 直角 C 等边 D 等腰直角
C3、在Rt△ABC中,∠C=90o,tanA=3,AC=1,则 S△ABC=( )
解:在Rt△ABC中:
∵tanA=
即 3 =∴ BC=3∴S△A BC =×1×3=观察与思考直接利用解直角三角形的有关知识进行解题。4、在△ABC中,∠A,∠B都是锐角,sinA= ,
tanB= AB=10,则△ABC的面积为( )看谁做的快4、如图在四边形ABCD中,AB=4- ,BC=1,
CD=3,∠B=135o, ∠C=90o,则∠D=( )
A 60 o B 67.5o C 75o D 不能确定B解:延长AB和DC的延长线相交于点E∵∠ABC=135o ∴∠EBC=45o∵∠BCD=90o ∴∠EBC=∠BEC=45o∴BC=EC=1在Rt△BCE中,BC2+CE2=BE2
∴BE=∴AE=AB+BE=(4- ) +即:AE=4 ∵CD=3 ∴ED=EC+CD=4∴AE=ED ∴∠A=∠D即∠D=∠A=67.5o活跃你的思维某四边形的形状如下图所示:
其中,∠A=60o,AB⊥BC,AD⊥CD,AB=20,CD=10
求AD、BC的长?(说出你的解题思路即可)
小小的收获:
(1)根据已知条件,构造直角三角形。
(2)在构造直角三角形的时候,尽量保持所给的已知条件的完整性。大显身手1、点M(-sin60o,cos60o)关于x轴对称的点的
坐标是( )
A( ,) B (- ,- )
C (- , ) D(- ,- )B
2、已知:A为锐角,tan(9oo- A)= ,则A=( )
30o3、在矩形ABCD中,若AD=1,AB= ,则该矩形的两对角线所成的锐角是( )
A 30 °B 45o C 60o D 75oC4、在△ABC中,∠C=90o,AC=BC=1,则sinA的值是( )
A B C 1 D A5、在△ABC中,∠C=90o,若cosA= ,
则tanB=( )6、如图在△ABC中,∠C=90o,D是AC边
上一点,且AD=BD=5,CD=3,
则tan∠CBD=( ); sinA=( ) 7、△ABC中,AB=AC=3,
则cosB=( )8、如图:AD⊥CD,AB=13,BC=12,CD=3,AD=4 ,则sinB=( )
A B C DA 一条小船从港口A出发,沿北偏东40o方向航行20海里后到
达B处,然后又沿北偏西30o方向航行10海里后到达C处,问
此时小船距港口A多少海里?(结果精确到1海里)以下数据
可以选用:sin40o≈0.6428 cos40o≈ 0.7660 tan40o≈0.8391实力检测思考解:过B作BE⊥AP,垂足为点E,过C点分别CD⊥AP,CF⊥BE,
垂足分别为点D、F,则四边形CDEF为矩形。
∴CD=EF,DE=CF ∵∠ QBC=30o,∴∠CBF=60o
∵AB=20,∠BAD=40o
∴AE=AB·cos40o≈20×0.7660≈15.3
BE=AB·sin40o≈20×0.6428≈12.856≈12.9
∵BC=10, ∠CBF=60o
∴CF=BC·sin60o≈10×0.866=0.866≈0.87
BF=BC·cos60=10×0.5=5
∴CD=EF=BE-BF=12.9-5=7.9
∵DE=CE≈8.7
∴AD=DE+AE≈15.3+8.7=24.0
∴由勾股定理得:AC2=AD2+CD2
AC2=24.02+7.92 即AC≈25
即此时小船距港口A约25海里
收获园地通过本节课的学习,我们掌握了:
1、特殊角的三角函数值。
2、在解直角三角形的时候,充分利用已知条
件,选择或构造直角三角形。
谢谢!
再见
1、特殊角的三角函数值12、在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c 、a、b ,其中除直角c 外,
其余的5个元素之间有以下的关系: ⑴ 三边之间的关系( )⑵ 锐角之间的关系( )⑶ 边角之间的关系:知识拓展如图:在直角三角形ABC中,
sinA= ( ) =cosB
sinB= ( ) =( )
cosA这是互为余角之间的函数关系认识一下方向角:仰角、俯角1、锐角A满足2sin(A-15o )= ,则 A=( )您能行75o解:∵2sin(A-15)o=
∴sin(A-15)o=
∴A-15o=60o 即 A=75o体验成功2、在△ABC,∠A, ∠B均为锐角,且∣tanB- |
+(2sinA- )2=0,则△ABC是( )三角形。
A 等腰 B 直角 C 等边 D 等腰直角
C3、在Rt△ABC中,∠C=90o,tanA=3,AC=1,则 S△ABC=( )
解:在Rt△ABC中:
∵tanA=
即 3 =∴ BC=3∴S△A BC =×1×3=观察与思考直接利用解直角三角形的有关知识进行解题。4、在△ABC中,∠A,∠B都是锐角,sinA= ,
tanB= AB=10,则△ABC的面积为( )看谁做的快4、如图在四边形ABCD中,AB=4- ,BC=1,
CD=3,∠B=135o, ∠C=90o,则∠D=( )
A 60 o B 67.5o C 75o D 不能确定B解:延长AB和DC的延长线相交于点E∵∠ABC=135o ∴∠EBC=45o∵∠BCD=90o ∴∠EBC=∠BEC=45o∴BC=EC=1在Rt△BCE中,BC2+CE2=BE2
∴BE=∴AE=AB+BE=(4- ) +即:AE=4 ∵CD=3 ∴ED=EC+CD=4∴AE=ED ∴∠A=∠D即∠D=∠A=67.5o活跃你的思维某四边形的形状如下图所示:
其中,∠A=60o,AB⊥BC,AD⊥CD,AB=20,CD=10
求AD、BC的长?(说出你的解题思路即可)
小小的收获:
(1)根据已知条件,构造直角三角形。
(2)在构造直角三角形的时候,尽量保持所给的已知条件的完整性。大显身手1、点M(-sin60o,cos60o)关于x轴对称的点的
坐标是( )
A( ,) B (- ,- )
C (- , ) D(- ,- )B
2、已知:A为锐角,tan(9oo- A)= ,则A=( )
30o3、在矩形ABCD中,若AD=1,AB= ,则该矩形的两对角线所成的锐角是( )
A 30 °B 45o C 60o D 75oC4、在△ABC中,∠C=90o,AC=BC=1,则sinA的值是( )
A B C 1 D A5、在△ABC中,∠C=90o,若cosA= ,
则tanB=( )6、如图在△ABC中,∠C=90o,D是AC边
上一点,且AD=BD=5,CD=3,
则tan∠CBD=( ); sinA=( ) 7、△ABC中,AB=AC=3,
则cosB=( )8、如图:AD⊥CD,AB=13,BC=12,CD=3,AD=4 ,则sinB=( )
A B C DA 一条小船从港口A出发,沿北偏东40o方向航行20海里后到
达B处,然后又沿北偏西30o方向航行10海里后到达C处,问
此时小船距港口A多少海里?(结果精确到1海里)以下数据
可以选用:sin40o≈0.6428 cos40o≈ 0.7660 tan40o≈0.8391实力检测思考解:过B作BE⊥AP,垂足为点E,过C点分别CD⊥AP,CF⊥BE,
垂足分别为点D、F,则四边形CDEF为矩形。
∴CD=EF,DE=CF ∵∠ QBC=30o,∴∠CBF=60o
∵AB=20,∠BAD=40o
∴AE=AB·cos40o≈20×0.7660≈15.3
BE=AB·sin40o≈20×0.6428≈12.856≈12.9
∵BC=10, ∠CBF=60o
∴CF=BC·sin60o≈10×0.866=0.866≈0.87
BF=BC·cos60=10×0.5=5
∴CD=EF=BE-BF=12.9-5=7.9
∵DE=CE≈8.7
∴AD=DE+AE≈15.3+8.7=24.0
∴由勾股定理得:AC2=AD2+CD2
AC2=24.02+7.92 即AC≈25
即此时小船距港口A约25海里
收获园地通过本节课的学习,我们掌握了:
1、特殊角的三角函数值。
2、在解直角三角形的时候,充分利用已知条
件,选择或构造直角三角形。
谢谢!
再见
