北师大版九年级数学下册 1.5三角函数的应用 试题(含详解)
文档属性
| 名称 | 北师大版九年级数学下册 1.5三角函数的应用 试题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 08:53:40 | ||
图片预览


文档简介
1.5三角函数的应用
一、单选题
1.已知一个斜坡的坡面长30米,铅直高度为15米,则这个斜坡的坡度为( )
A. B. C. D.
2.如图,在综合实践活动中,嘉嘉在学校门口的点A处测得树的顶端的仰角为,同时测得米,则树的高为( )
A.米 B.米 C.米 D.米
3.位于河南省三门峡市的三门峡大坝诞生于1957年,被誉为“万里黄河第一坝”.它的建成不仅为黄河流域的灌溉和发电提供了重要的保障,也为国家的经济发展和生态环境保护做出了贡献.如图,大坝的横截面为梯形,迎水坡的坡角为,坡度约为,坝面宽,坝高约为,则坝底的长约为( )
A. B. C. D.
4.河堤横断面如图,堤高米,迎水坡的坡比是,则的长是( )
A.米 B.10米 C.15米 D.米
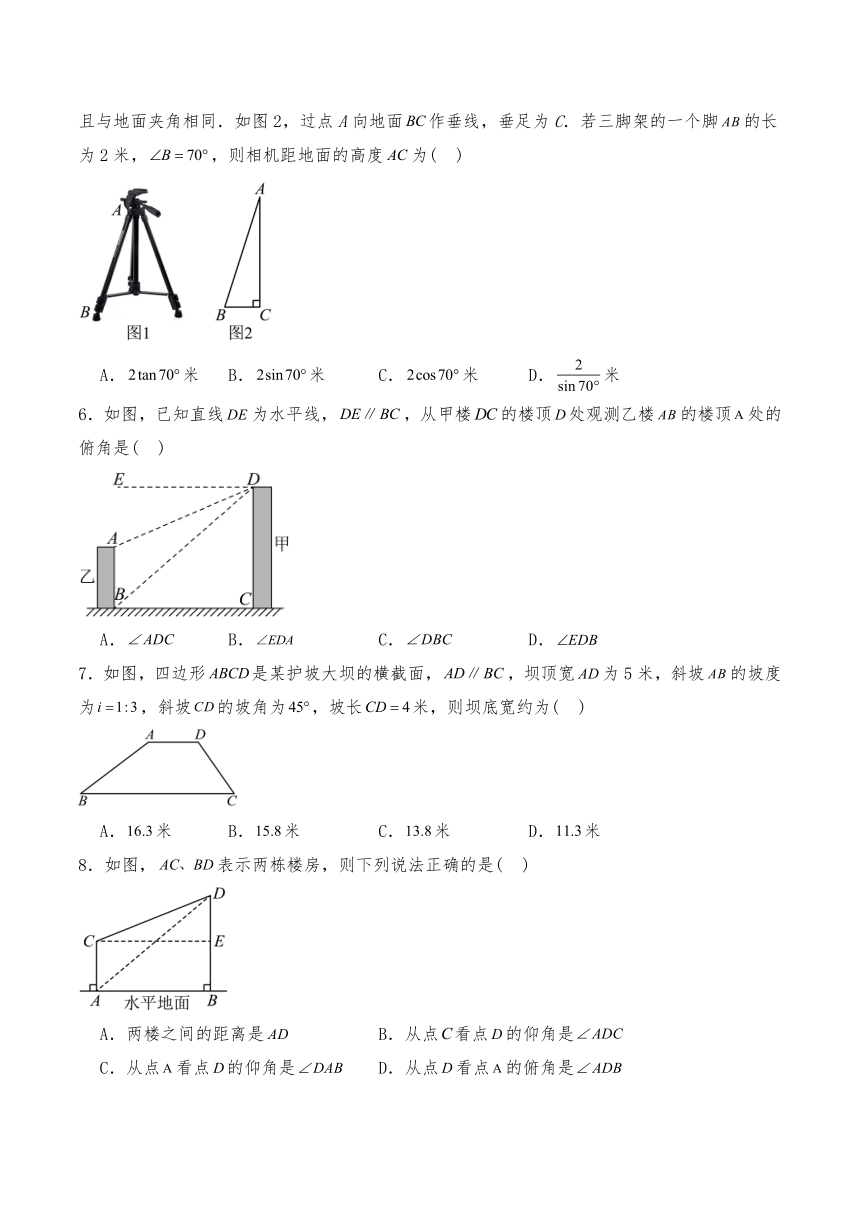
5.学校摄影兴趣小组在上摄影课,小王发现摄影三脚架如图1所示,该支架三个脚长度相同且与地面夹角相同.如图2,过点A向地面作垂线,垂足为C.若三脚架的一个脚的长为2米,,则相机距地面的高度为( )
A.米 B.米 C.米 D.米
6.如图,已知直线为水平线,,从甲楼的楼顶处观测乙楼的楼顶处的俯角是( )
A. B. C. D.
7.如图,四边形是某护坡大坝的横截面,,坝顶宽为5米,斜坡的坡度为,斜坡的坡角为,坡长米,则坝底宽约为( )
A.米 B.米 C.米 D.米
8.如图,表示两栋楼房,则下列说法正确的是( )
A.两楼之间的距离是 B.从点看点的仰角是
C.从点看点的仰角是 D.从点看点的俯角是
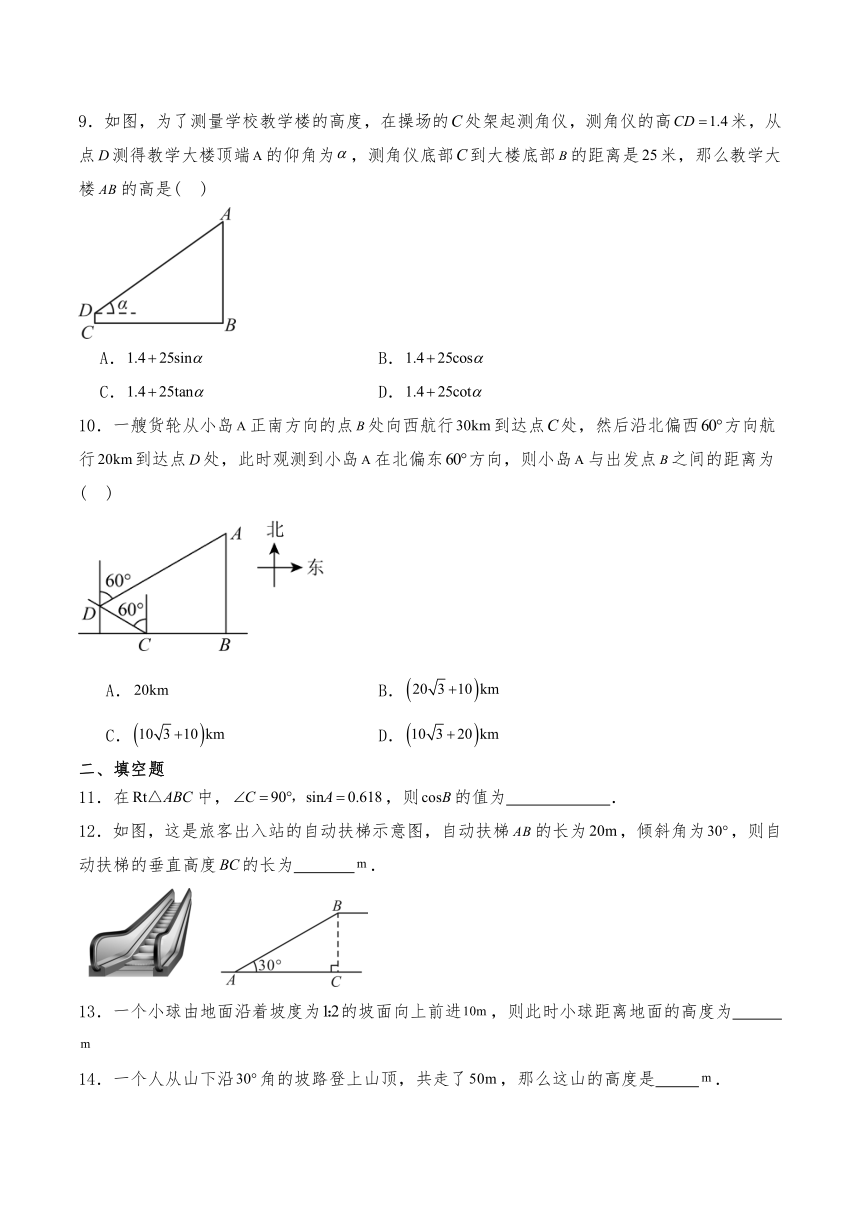
9.如图,为了测量学校教学楼的高度,在操场的处架起测角仪,测角仪的高米,从点测得教学大楼顶端的仰角为,测角仪底部到大楼底部的距离是米,那么教学大楼的高是( )
A. B.
C. D.
10.一艘货轮从小岛正南方向的点处向西航行到达点处,然后沿北偏西方向航行到达点处,此时观测到小岛在北偏东方向,则小岛与出发点之间的距离为( )
A. B.
C. D.
二、填空题
11.在中,,则的值为 .
12.如图,这是旅客出入站的自动扶梯示意图,自动扶梯的长为,倾斜角为,则自动扶梯的垂直高度的长为 .
13.一个小球由地面沿着坡度为的坡面向上前进,则此时小球距离地面的高度为
14.一个人从山下沿角的坡路登上山顶,共走了,那么这山的高度是 .
15.如图,坡角为的斜坡上有一棵大树(垂直于水平地面),当太阳光线与水平线成角沿斜坡照下时,在斜坡上树影的长为30米,则大树的高为 .
16.某人在大厦一层乘坐观光电梯,看到大厦外一棵树上的鸟巢,仰角为,到达大厦的第五层后,再看这个鸟巢,俯角为,已知大厦的层高均为,则这棵树与大厦的距离为 m.
17.北斗卫星导航系统是中国自行硏制的全球卫星导航系统,其由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶10千米至B地,再沿北偏东60°方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东方向.则的度数为 ;B、C两地的距离是 .(结果保留根号)
18.如图,为了测得某建筑物的高度,在处用高为的测角仪,测得该建筑物顶端的仰角为,再向建筑物方向前进,又测得该建筑物顶端A的仰角为,则该建筑物的高度为 (结果保留根号)
三、解答题
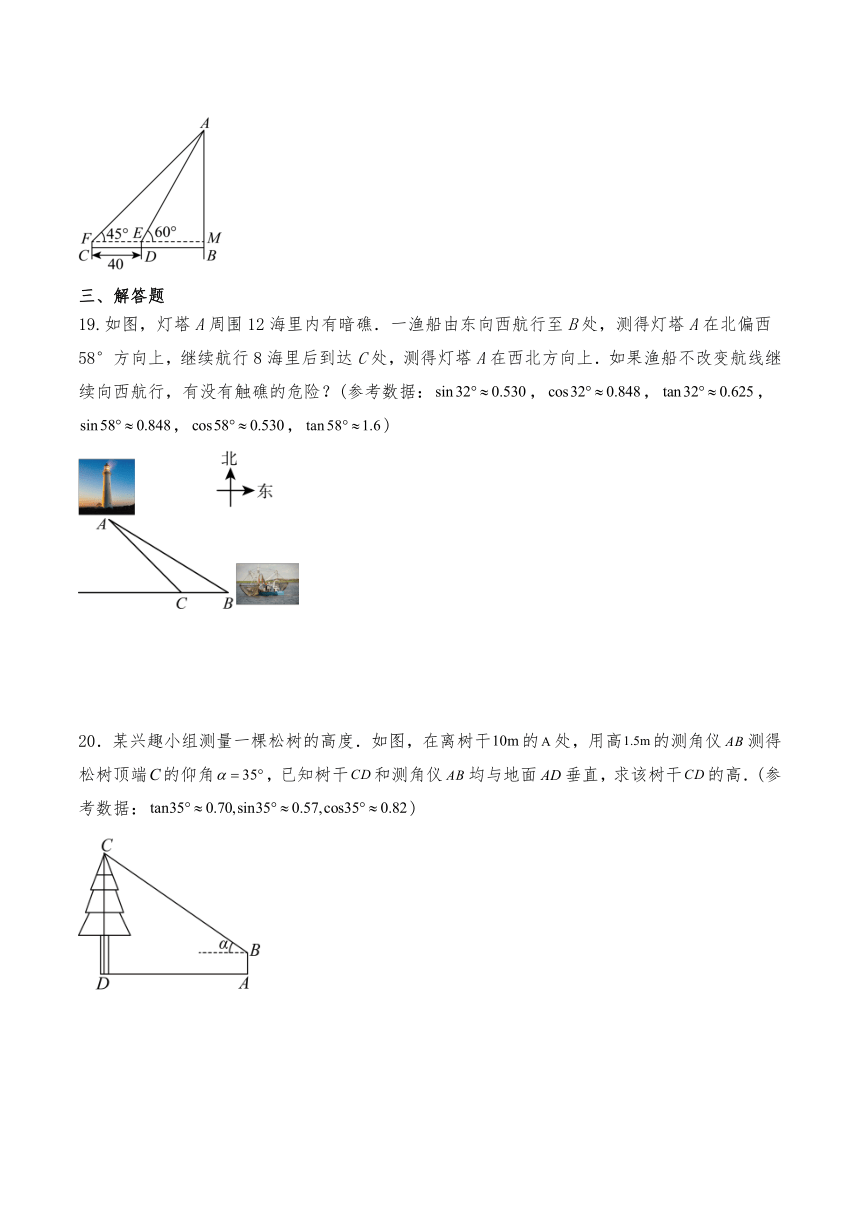
19.如图,灯塔A周围12海里内有暗礁.一渔船由东向西航行至B处,测得灯塔A在北偏西58°方向上,继续航行8海里后到达C处,测得灯塔A在西北方向上.如果渔船不改变航线继续向西航行,有没有触礁的危险?(参考数据:,,,,,)
20.某兴趣小组测量一棵松树的高度.如图,在离树干的处,用高的测角仪测得松树顶端的仰角,已知树干和测角仪均与地面垂直,求该树干的高.(参考数据:)
21.为弘扬革命传统精神,清明期间,某校组织学生前往烈士陵园缅怀革命先烈.大家被革命烈士纪念碑的雄伟壮观震撼,想知道纪念碑的通高(碑顶到水平地面的距离),于是师生组成综合实践小组进行测量.他们在地面的A点用测角仪测得碑顶D的仰角为,在B点处测得碑顶D的仰角为,已知,测角仪的高度是在同一直线上),根据以上数据求烈士纪念碑的通高.(,结果保留一位小数)
22.如图,平地上一幢建筑物与铁塔相距60米,在建筑物顶部测得铁塔底部的俯角为,测得铁塔顶部的仰角为,求:
(1)建筑物高(精确到1米);
(2)求铁塔的高度(精确到1米).(已知,)
23.近几年,中国的无人机技术发展迅速,处于世界领先水平.月日,南阳市某中学组织了“无人机进校园”活动,用科技结合所学知识,为孩子们点亮科技梦.如图,无人机操控者在一综合楼外放飞无人机,当无人机飞行到一定高度处时,无人机测得操控者的俯角为,测得综合楼的顶点处的俯角为.已知操控者和综合楼之间的距离为,综合楼的高度为.求此时无人机的高度.(假设点,,,都在同一平面内.参考数据:,,)
24.如图,在一条水平的码头上有两处灯塔A和B,在灯塔处测得某一渔船位于北偏西方向的处,当渔船沿着正北方向前进到达处时,在灯塔处测得处位于西北方向.已知,求处到码头的距离.
25.如图,市民甲在处看见飞机的仰角为,同时另一市民乙在斜坡上的处看见飞机的仰角为.若斜坡的坡比,铅垂高度米(点在同一水平线上).
(1)两位市民甲、乙之间的距离;
(2)此时飞机的高度.(结果保留根号)
26.嘉淇看到这样一道题目:
如图,某巡逻船在处测得一艘敌舰在北偏东的处,卫星测得相距海里,巡逻船静止不动,分钟后测得该敌舰在巡逻船的北偏东的处,此时卫星信号突然中断,已知该敌舰的航速为海里/小时.(结果保留整数,参考数据:,,,)
嘉淇过点作于,设海里,请你帮她接着解决以下问题:
(1)______里(用含用的代数式表示);
(2)求敌舰在处时与巡逻船的距离.
答案
一、单选题
1.C
【分析】此题主要考查了解直角三角形的应用,设坡角为,则,得出,进而根据坡度的定义,即可求解.
【详解】解:依题意,设坡角为,则
∴,
∴这个斜坡的坡度为,
故选:C.
2.A
【分析】本题主要考查解直角三角形,熟练掌握三角函数的定义是解题的关键.
【详解】解:∵为直角三角形,,
∴,
即,
∴(米);
故选:A.
3.D
【分析】本题主要考查了解直角三角形的实际应用,矩形的性质与判定,过点B作于E,先证明四边形是矩形,得到,再解得到,由此即可求出答案.
【详解】解:如图所示,过点B作于E,
由题意得,
∴,
又∵,
∴四边形是矩形,
∴,
在中,,
∴,
∴,
故选D.
4.A
【分析】本题考查了坡比计算,熟练掌握定义是解题的关键.
【详解】∵堤高米,迎水坡的坡比是,
∴,
解得(米),
故选A.
5.B
【分析】本此题主要考查了解直角三角形的应用,直接利用锐角三角函数关系得出,进而得出答案.
【详解】解:∵三脚架的一个脚的长为2米,,
∴,
∴( 米).
故选:B.
6.B
【分析】本题考查了俯角的定义,根据俯角是往下看,观测者的视线与水平线的夹角即为俯角,结合图形,即可求解.
【详解】解:∵直线为水平线,,
∴从甲楼的楼顶处观测乙楼的楼顶处的俯角是,
故选:B.
7.A
【分析】本题考查解直角三角形的应用.过点A、D作的垂线,垂足分别为E、F,证明四边形是矩形,是等腰直角三角形,解直角三角形即可求解.
【详解】解:过点A、D作的垂线,垂足分别为E、F,
∵,
∴四边形是矩形,
∵斜坡的坡角为,
∴是等腰直角三角形,
∵米,
∴,
∴,
∵斜坡的坡度为,
∴,
∴(米).
故选:A.
8.C
【分析】本题考查了解直角三角形—俯角、仰角的定义,根据俯角、仰角的定义解答即可,熟练掌握俯角、仰角的定义是解此题的关键.
【详解】解:A、两楼之间的距离是,故原说法不正确,不符合题意;
B、从点看点的仰角是,故原说法不正确,不符合题意;
C、从点看点的仰角是,故原说法正确,符合题意;
D、从点看点的俯角是,故原说法不正确,不符合题意;
故选:C.
9.C
【分析】此题考查了仰角问题,过作于点,则四边形是矩形,根据性质和三角函数即可求解,解题的关键是添加辅助线构造直角三角形,熟练掌握三角函数的应用.
【详解】如图,过作于点,
则有四边形是矩形,
∴米,米,,
在中,,
∴,
∴,
故选:.
10.D
【分析】本题考查了解直角三角形的应用,方向角,矩形的判定与性质,锐角三角函数定义,熟练掌握相关性质,熟悉锐角三角函数定义是解答本题的关键.
过点作于点,过点作于点,得到四边形是矩形,,,由直角三角形的性质得到,再根据锐角三角函数定义得到,由此得到答案.
【详解】解:如图所示,过点作于点,过点作于点,
,
四边形是矩形,
,,
由题意得:
,
,
,
,
,
,
,
.
故选:.
二、填空题
11.0.618
【分析】本题考查互余两角的三角函数的关系,掌握任意锐角的正弦值等于余角的余弦值,任意锐角的余弦值等于余角的正弦值是解题关键.由题意可得出,从而根据互余两角的三角函数的关系即可得出.
【详解】解:∵在中,,
∴,
∴,
故答案为:0.618.
12.
【分析】本题考查了解直角三角形的应用.熟练掌握是解题的关键.
由题意知,根据,计算求解即可.
【详解】解,由题意知,,
故答案为:.
13.
【分析】本题主要考查了解直角三角形的实际应用,勾股定理,过点B作,根据,则设,,由勾股定理得,,即,进行计算即可得到答案.
【详解】解:如图所示,斜坡的坡度为,,过点B作,
在,,
∴设,,
由勾股定理得,,
∴,
解得(负值舍去),
∴,即此时小球距离地面的高度为,
故答案为:.
14.
【分析】本题考查了解直角三角形的应用一坡度坡角问题,根据含角所对的直角边等于斜边的一半计算即可求解,掌握含角的直角三角形的性质是解题的关键.
【详解】解:根据题意可得,山的高度,
故答案为:.
15.米
【分析】本题考查的是解直角三角形的应用—坡度坡角问题,正确作出辅助线、熟记锐角三角函数的定义是解题的关键,过点作,交的延长线于,根据余弦的定义求出,根据直角三角形的性质求出,结合图形计算,得到答案.
【详解】解:如图,过点作,交的延长线于,
,
则,
米,
米,米,
在中,,
米,
米,
故答案为:米.
16.
【分析】本题考查的是解直角三角形的实际应用,理解仰角与俯角的含义是解本题的关键,先画出图形,过作于,则,四边形为矩形,再进一步解决即可.
【详解】解:如图,由题意可得:,,,
过作于,则,四边形为矩形,
∴,,,,
∴,,,
∴,解得:,
∴,
∴这棵树与大厦的距离为;
故答案为:
17.
【分析】本题考查了解直角三角形的应用方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.过点作,垂足为,根据题意可得:,,,,从而可得,然后利用平角定义可得,从而利用三角形内角和定理进行计算,求出的度数;先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义求出的长,即可解答.
【详解】解:如图,过点作,垂足为,
由题意得:,,,,
,
,
,
,
的度数为;
在中,千米,,
(千米),
在中,,
(千米),
,两地的距离为千米.
故答案为:,
18.
【分析】本题考查解直角三角形的应用,设米,利用正切的定义用x表示出,,根据列方程,即可求解.
【详解】解:由题意知,,,
设,
在中,,
则,
在中,,
则,
,
,
解得,
,
故答案为:.
三、解答题
19.解:过点作,由题意,得:,,,
设,
在中,,
∴,
∴,
在中,,
∴,
∴,
∵,
∴渔船没有触礁的危险.
20.解:如图,过点作于点,则四边形是矩形,
∵,
.
在中,,
,
,即树干的高约为8.5m
21.解:由题意得:,
∵是的外角,
在中,(m),
.
答:烈士纪念碑的通高约为.
22.(1)解:过A点作于E点,
则四边形为矩形,
∴,,
∵,,
∴米;
(2)∵,
∴,
∴,
∴,
∴米.
23.解:如图,过点作于点,过点作于点.则四边形为矩形.
∴,.
∵无人机测得操控者的俯角为,测得综合楼的顶点处的俯角为
∴,,
∴.
∵,
∴.
设,则.
∴.
∵,
∴.
解得,.
∴.
∴此时无人机的高度约为.
24.解:如图,延长交直线于点.
,
设长为,则.
在中,,
.
又,
.
在中,,
.
,
解得,
.
答:处到码头的距离约为.
25.(1)解:∵斜坡CF的坡比,铅垂高度米,
∴,
∴米,
∴米;
(2)如图所示,过点D作于H,则四边形是矩形,
∴米,,
∵,,
∴是等腰直角三角形,
∴,
设米,则米,米,
在中,,
∴,
解得,
∴米.
26.(1)解:根据题意得, ,(海里),
在中,海里,
∴,
∴,
∴海里,
故答案为:;
(2)解:∵,
∴,
∴,
即,
解得,,
∵,
∴不合,舍去,
∴,
又,
即,
∴(负值舍去),
∴(海里) ,
答:敌舰在处时与巡逻船的距离为海里.
一、单选题
1.已知一个斜坡的坡面长30米,铅直高度为15米,则这个斜坡的坡度为( )
A. B. C. D.
2.如图,在综合实践活动中,嘉嘉在学校门口的点A处测得树的顶端的仰角为,同时测得米,则树的高为( )
A.米 B.米 C.米 D.米
3.位于河南省三门峡市的三门峡大坝诞生于1957年,被誉为“万里黄河第一坝”.它的建成不仅为黄河流域的灌溉和发电提供了重要的保障,也为国家的经济发展和生态环境保护做出了贡献.如图,大坝的横截面为梯形,迎水坡的坡角为,坡度约为,坝面宽,坝高约为,则坝底的长约为( )
A. B. C. D.
4.河堤横断面如图,堤高米,迎水坡的坡比是,则的长是( )
A.米 B.10米 C.15米 D.米
5.学校摄影兴趣小组在上摄影课,小王发现摄影三脚架如图1所示,该支架三个脚长度相同且与地面夹角相同.如图2,过点A向地面作垂线,垂足为C.若三脚架的一个脚的长为2米,,则相机距地面的高度为( )
A.米 B.米 C.米 D.米
6.如图,已知直线为水平线,,从甲楼的楼顶处观测乙楼的楼顶处的俯角是( )
A. B. C. D.
7.如图,四边形是某护坡大坝的横截面,,坝顶宽为5米,斜坡的坡度为,斜坡的坡角为,坡长米,则坝底宽约为( )
A.米 B.米 C.米 D.米
8.如图,表示两栋楼房,则下列说法正确的是( )
A.两楼之间的距离是 B.从点看点的仰角是
C.从点看点的仰角是 D.从点看点的俯角是
9.如图,为了测量学校教学楼的高度,在操场的处架起测角仪,测角仪的高米,从点测得教学大楼顶端的仰角为,测角仪底部到大楼底部的距离是米,那么教学大楼的高是( )
A. B.
C. D.
10.一艘货轮从小岛正南方向的点处向西航行到达点处,然后沿北偏西方向航行到达点处,此时观测到小岛在北偏东方向,则小岛与出发点之间的距离为( )
A. B.
C. D.
二、填空题
11.在中,,则的值为 .
12.如图,这是旅客出入站的自动扶梯示意图,自动扶梯的长为,倾斜角为,则自动扶梯的垂直高度的长为 .
13.一个小球由地面沿着坡度为的坡面向上前进,则此时小球距离地面的高度为
14.一个人从山下沿角的坡路登上山顶,共走了,那么这山的高度是 .
15.如图,坡角为的斜坡上有一棵大树(垂直于水平地面),当太阳光线与水平线成角沿斜坡照下时,在斜坡上树影的长为30米,则大树的高为 .
16.某人在大厦一层乘坐观光电梯,看到大厦外一棵树上的鸟巢,仰角为,到达大厦的第五层后,再看这个鸟巢,俯角为,已知大厦的层高均为,则这棵树与大厦的距离为 m.
17.北斗卫星导航系统是中国自行硏制的全球卫星导航系统,其由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶10千米至B地,再沿北偏东60°方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东方向.则的度数为 ;B、C两地的距离是 .(结果保留根号)
18.如图,为了测得某建筑物的高度,在处用高为的测角仪,测得该建筑物顶端的仰角为,再向建筑物方向前进,又测得该建筑物顶端A的仰角为,则该建筑物的高度为 (结果保留根号)
三、解答题
19.如图,灯塔A周围12海里内有暗礁.一渔船由东向西航行至B处,测得灯塔A在北偏西58°方向上,继续航行8海里后到达C处,测得灯塔A在西北方向上.如果渔船不改变航线继续向西航行,有没有触礁的危险?(参考数据:,,,,,)
20.某兴趣小组测量一棵松树的高度.如图,在离树干的处,用高的测角仪测得松树顶端的仰角,已知树干和测角仪均与地面垂直,求该树干的高.(参考数据:)
21.为弘扬革命传统精神,清明期间,某校组织学生前往烈士陵园缅怀革命先烈.大家被革命烈士纪念碑的雄伟壮观震撼,想知道纪念碑的通高(碑顶到水平地面的距离),于是师生组成综合实践小组进行测量.他们在地面的A点用测角仪测得碑顶D的仰角为,在B点处测得碑顶D的仰角为,已知,测角仪的高度是在同一直线上),根据以上数据求烈士纪念碑的通高.(,结果保留一位小数)
22.如图,平地上一幢建筑物与铁塔相距60米,在建筑物顶部测得铁塔底部的俯角为,测得铁塔顶部的仰角为,求:
(1)建筑物高(精确到1米);
(2)求铁塔的高度(精确到1米).(已知,)
23.近几年,中国的无人机技术发展迅速,处于世界领先水平.月日,南阳市某中学组织了“无人机进校园”活动,用科技结合所学知识,为孩子们点亮科技梦.如图,无人机操控者在一综合楼外放飞无人机,当无人机飞行到一定高度处时,无人机测得操控者的俯角为,测得综合楼的顶点处的俯角为.已知操控者和综合楼之间的距离为,综合楼的高度为.求此时无人机的高度.(假设点,,,都在同一平面内.参考数据:,,)
24.如图,在一条水平的码头上有两处灯塔A和B,在灯塔处测得某一渔船位于北偏西方向的处,当渔船沿着正北方向前进到达处时,在灯塔处测得处位于西北方向.已知,求处到码头的距离.
25.如图,市民甲在处看见飞机的仰角为,同时另一市民乙在斜坡上的处看见飞机的仰角为.若斜坡的坡比,铅垂高度米(点在同一水平线上).
(1)两位市民甲、乙之间的距离;
(2)此时飞机的高度.(结果保留根号)
26.嘉淇看到这样一道题目:
如图,某巡逻船在处测得一艘敌舰在北偏东的处,卫星测得相距海里,巡逻船静止不动,分钟后测得该敌舰在巡逻船的北偏东的处,此时卫星信号突然中断,已知该敌舰的航速为海里/小时.(结果保留整数,参考数据:,,,)
嘉淇过点作于,设海里,请你帮她接着解决以下问题:
(1)______里(用含用的代数式表示);
(2)求敌舰在处时与巡逻船的距离.
答案
一、单选题
1.C
【分析】此题主要考查了解直角三角形的应用,设坡角为,则,得出,进而根据坡度的定义,即可求解.
【详解】解:依题意,设坡角为,则
∴,
∴这个斜坡的坡度为,
故选:C.
2.A
【分析】本题主要考查解直角三角形,熟练掌握三角函数的定义是解题的关键.
【详解】解:∵为直角三角形,,
∴,
即,
∴(米);
故选:A.
3.D
【分析】本题主要考查了解直角三角形的实际应用,矩形的性质与判定,过点B作于E,先证明四边形是矩形,得到,再解得到,由此即可求出答案.
【详解】解:如图所示,过点B作于E,
由题意得,
∴,
又∵,
∴四边形是矩形,
∴,
在中,,
∴,
∴,
故选D.
4.A
【分析】本题考查了坡比计算,熟练掌握定义是解题的关键.
【详解】∵堤高米,迎水坡的坡比是,
∴,
解得(米),
故选A.
5.B
【分析】本此题主要考查了解直角三角形的应用,直接利用锐角三角函数关系得出,进而得出答案.
【详解】解:∵三脚架的一个脚的长为2米,,
∴,
∴( 米).
故选:B.
6.B
【分析】本题考查了俯角的定义,根据俯角是往下看,观测者的视线与水平线的夹角即为俯角,结合图形,即可求解.
【详解】解:∵直线为水平线,,
∴从甲楼的楼顶处观测乙楼的楼顶处的俯角是,
故选:B.
7.A
【分析】本题考查解直角三角形的应用.过点A、D作的垂线,垂足分别为E、F,证明四边形是矩形,是等腰直角三角形,解直角三角形即可求解.
【详解】解:过点A、D作的垂线,垂足分别为E、F,
∵,
∴四边形是矩形,
∵斜坡的坡角为,
∴是等腰直角三角形,
∵米,
∴,
∴,
∵斜坡的坡度为,
∴,
∴(米).
故选:A.
8.C
【分析】本题考查了解直角三角形—俯角、仰角的定义,根据俯角、仰角的定义解答即可,熟练掌握俯角、仰角的定义是解此题的关键.
【详解】解:A、两楼之间的距离是,故原说法不正确,不符合题意;
B、从点看点的仰角是,故原说法不正确,不符合题意;
C、从点看点的仰角是,故原说法正确,符合题意;
D、从点看点的俯角是,故原说法不正确,不符合题意;
故选:C.
9.C
【分析】此题考查了仰角问题,过作于点,则四边形是矩形,根据性质和三角函数即可求解,解题的关键是添加辅助线构造直角三角形,熟练掌握三角函数的应用.
【详解】如图,过作于点,
则有四边形是矩形,
∴米,米,,
在中,,
∴,
∴,
故选:.
10.D
【分析】本题考查了解直角三角形的应用,方向角,矩形的判定与性质,锐角三角函数定义,熟练掌握相关性质,熟悉锐角三角函数定义是解答本题的关键.
过点作于点,过点作于点,得到四边形是矩形,,,由直角三角形的性质得到,再根据锐角三角函数定义得到,由此得到答案.
【详解】解:如图所示,过点作于点,过点作于点,
,
四边形是矩形,
,,
由题意得:
,
,
,
,
,
,
,
.
故选:.
二、填空题
11.0.618
【分析】本题考查互余两角的三角函数的关系,掌握任意锐角的正弦值等于余角的余弦值,任意锐角的余弦值等于余角的正弦值是解题关键.由题意可得出,从而根据互余两角的三角函数的关系即可得出.
【详解】解:∵在中,,
∴,
∴,
故答案为:0.618.
12.
【分析】本题考查了解直角三角形的应用.熟练掌握是解题的关键.
由题意知,根据,计算求解即可.
【详解】解,由题意知,,
故答案为:.
13.
【分析】本题主要考查了解直角三角形的实际应用,勾股定理,过点B作,根据,则设,,由勾股定理得,,即,进行计算即可得到答案.
【详解】解:如图所示,斜坡的坡度为,,过点B作,
在,,
∴设,,
由勾股定理得,,
∴,
解得(负值舍去),
∴,即此时小球距离地面的高度为,
故答案为:.
14.
【分析】本题考查了解直角三角形的应用一坡度坡角问题,根据含角所对的直角边等于斜边的一半计算即可求解,掌握含角的直角三角形的性质是解题的关键.
【详解】解:根据题意可得,山的高度,
故答案为:.
15.米
【分析】本题考查的是解直角三角形的应用—坡度坡角问题,正确作出辅助线、熟记锐角三角函数的定义是解题的关键,过点作,交的延长线于,根据余弦的定义求出,根据直角三角形的性质求出,结合图形计算,得到答案.
【详解】解:如图,过点作,交的延长线于,
,
则,
米,
米,米,
在中,,
米,
米,
故答案为:米.
16.
【分析】本题考查的是解直角三角形的实际应用,理解仰角与俯角的含义是解本题的关键,先画出图形,过作于,则,四边形为矩形,再进一步解决即可.
【详解】解:如图,由题意可得:,,,
过作于,则,四边形为矩形,
∴,,,,
∴,,,
∴,解得:,
∴,
∴这棵树与大厦的距离为;
故答案为:
17.
【分析】本题考查了解直角三角形的应用方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.过点作,垂足为,根据题意可得:,,,,从而可得,然后利用平角定义可得,从而利用三角形内角和定理进行计算,求出的度数;先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义求出的长,即可解答.
【详解】解:如图,过点作,垂足为,
由题意得:,,,,
,
,
,
,
的度数为;
在中,千米,,
(千米),
在中,,
(千米),
,两地的距离为千米.
故答案为:,
18.
【分析】本题考查解直角三角形的应用,设米,利用正切的定义用x表示出,,根据列方程,即可求解.
【详解】解:由题意知,,,
设,
在中,,
则,
在中,,
则,
,
,
解得,
,
故答案为:.
三、解答题
19.解:过点作,由题意,得:,,,
设,
在中,,
∴,
∴,
在中,,
∴,
∴,
∵,
∴渔船没有触礁的危险.
20.解:如图,过点作于点,则四边形是矩形,
∵,
.
在中,,
,
,即树干的高约为8.5m
21.解:由题意得:,
∵是的外角,
在中,(m),
.
答:烈士纪念碑的通高约为.
22.(1)解:过A点作于E点,
则四边形为矩形,
∴,,
∵,,
∴米;
(2)∵,
∴,
∴,
∴,
∴米.
23.解:如图,过点作于点,过点作于点.则四边形为矩形.
∴,.
∵无人机测得操控者的俯角为,测得综合楼的顶点处的俯角为
∴,,
∴.
∵,
∴.
设,则.
∴.
∵,
∴.
解得,.
∴.
∴此时无人机的高度约为.
24.解:如图,延长交直线于点.
,
设长为,则.
在中,,
.
又,
.
在中,,
.
,
解得,
.
答:处到码头的距离约为.
25.(1)解:∵斜坡CF的坡比,铅垂高度米,
∴,
∴米,
∴米;
(2)如图所示,过点D作于H,则四边形是矩形,
∴米,,
∵,,
∴是等腰直角三角形,
∴,
设米,则米,米,
在中,,
∴,
解得,
∴米.
26.(1)解:根据题意得, ,(海里),
在中,海里,
∴,
∴,
∴海里,
故答案为:;
(2)解:∵,
∴,
∴,
即,
解得,,
∵,
∴不合,舍去,
∴,
又,
即,
∴(负值舍去),
∴(海里) ,
答:敌舰在处时与巡逻船的距离为海里.
