北师大版九年级数学下册 2.1二次函数 试题 (含详解)
文档属性
| 名称 | 北师大版九年级数学下册 2.1二次函数 试题 (含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 602.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 08:57:25 | ||
图片预览



文档简介
2.1二次函数
一、单选题
1.下列各式中,y是x的二次函数的是( )
A. B. C. D.
2.如图,一个正方体的边长为,它的表面积为,则y与x的函数关系式为( )
A. B. C. D.
3.若是关于的二次函数,则的值为( )
A. B.0 C.2 D.
4.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为( )
A. B. C. D.
5.某商店购进某种商品的价格是7.5元/件,在一段时间里,单价是13.5元,销售量是500件,而单价每降低1元就可多售出200件,当销售价为元/件()时,获取利润元,则与的函数关系为( )
A. B.
C. D.以上答案都不对
6.据省统计局公布的数据,合肥市2023年第一季度总值约为2.6千亿元人民币,若我市第三季度总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A. B.
C. D.
7.已知某种产品的成本价为30元/千克,经市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:.设这种产品每天的销售利润为w(元),则w与x之间的函数表达式为( )
A. B.
C. D.
8.正方形的边长为3,若边长增加,则面积增加,与的关系式为( )
A. B.
C. D.
9.函数的图象是抛物线,则实数的取值范围是( )
A. B. C. D.且
10.如图,是等腰直角三角形,,,点为边上一点,过点作,,垂足分别为,,点从点出发沿运动至点.设,,四边形的面积为,在运动过程中,下列说法正确的是( )
A.y与x满足一次函数关系,S与x满足二次函数关系,且S存在最大值
B.y与x满足一次函数关系,S与x满足二次函数关系,且S存在最小值
C.y与x满足反比例函数关系,S与x满足二次函数关系,且S存在最大值
D.y与x满足反比例函数关系,S与x满足二次函数关系,且S存在最小值
二、填空题
11.下列函数①;②;③;④;⑤.其中是二次函数的是 .
12.已知二次函数,则 .
13.如图,矩形绿地的长和宽分别为和.若将该绿地的长、宽各增加,扩充后的绿地的面积为,则y与x之间的函数关系是 .(填“正比例函数关系”、“一次函数关系”或“二次函数关系”)
14.二次函数的二次项是 ,一次项系数是 ,常数项是 .
15.用长为30米的栅栏围成一个矩形花坛,其中一边长为x米,面积为y平方米,则y与x的函数关系为 (不要求写自变量取值范围).
16.某工厂本年度的产值为100万元,若在今后两年里产值的年增长率均为x,两年后的产值为y万元.那么y关于x的函数解析式是 .
17.相框边的宽窄影响可放入相片的大小.如图,相框长,宽,相框边的宽为,相框内的面积是,则y与x之间的函数关系式为 .
18.正方形边长,若边长增加,增加后正方形的面积为,与的函数关系式为 .
三、解答题
19.当为何值时,函数是二次函数.
20.已知函数.
(1)当函数是二次函数时,求的值:
(2)当函数是一次函数时,求的值.
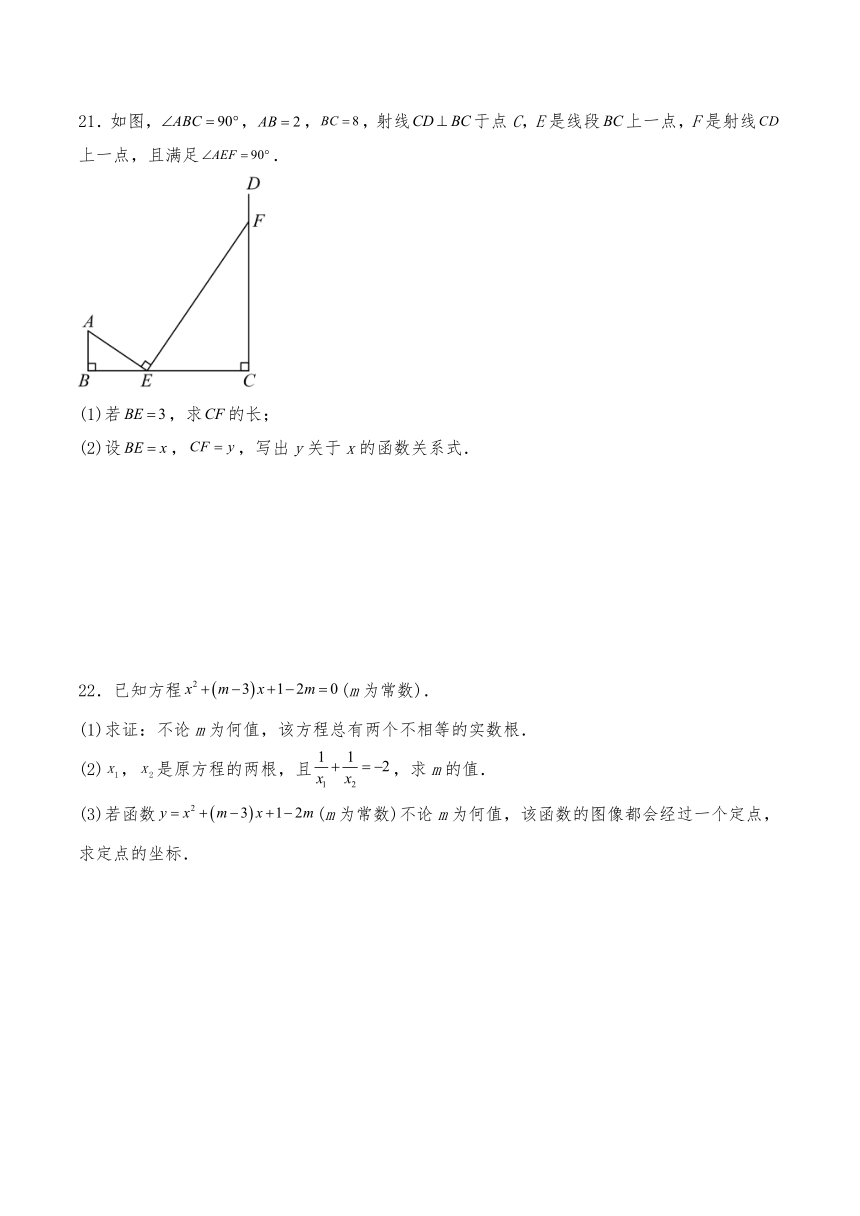
21.如图,,,,射线于点C,E是线段上一点,F是射线上一点,且满足.
(1)若,求的长;
(2)设,,写出y关于x的函数关系式.
22.已知方程(m为常数).
(1)求证:不论m为何值,该方程总有两个不相等的实数根.
(2),是原方程的两根,且,求m的值.
(3)若函数(m为常数)不论m为何值,该函数的图像都会经过一个定点,求定点的坐标.
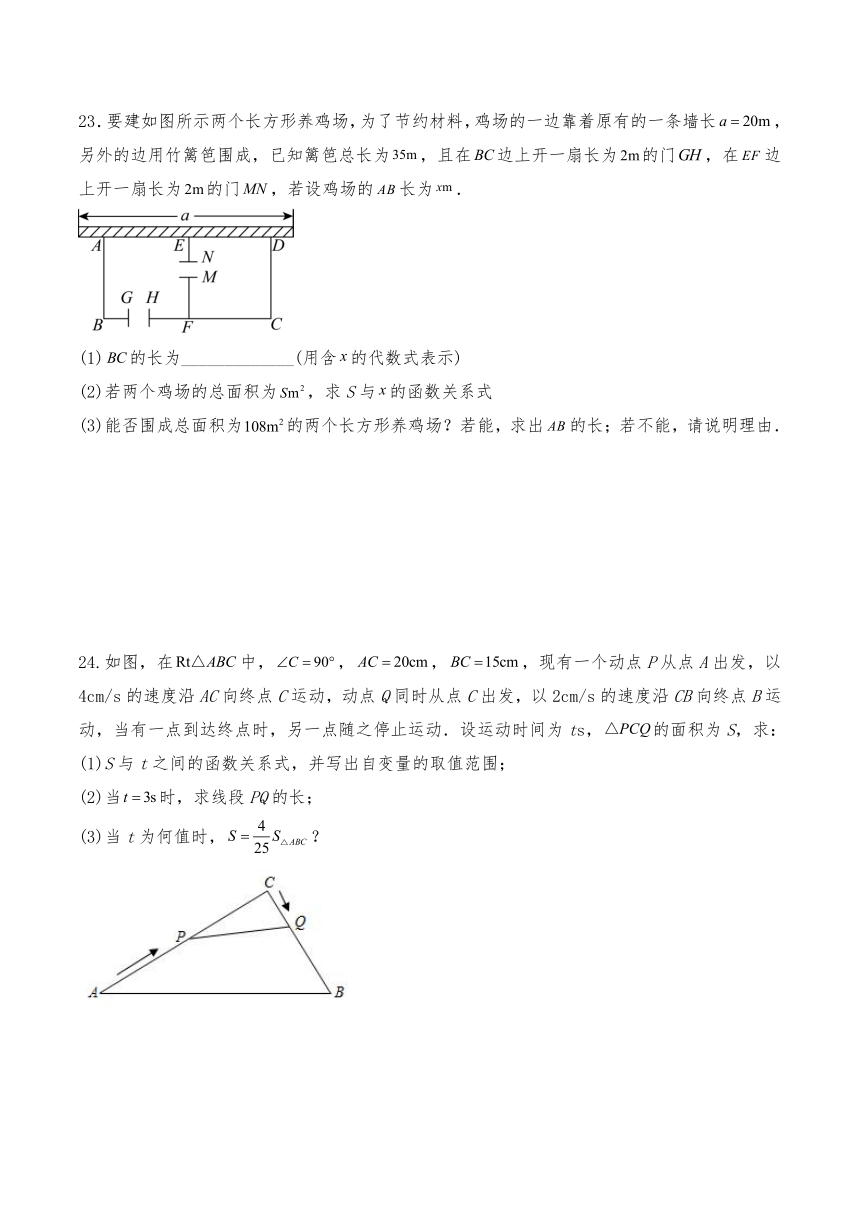
23.要建如图所示两个长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙长,另外的边用竹篱笆围成,已知篱笆总长为,且在边上开一扇长为的门,在边上开一扇长为的门,若设鸡场的长为.
(1)的长为_____________(用含的代数式表示)
(2)若两个鸡场的总面积为,求S与的函数关系式
(3)能否围成总面积为的两个长方形养鸡场?若能,求出的长;若不能,请说明理由.
24.如图,在中,,,,现有一个动点P从点A出发,以4cm/s的速度沿AC向终点C运动,动点Q同时从点C出发,以2cm/s的速度沿CB向终点B运动,当有一点到达终点时,另一点随之停止运动.设运动时间为ts,的面积为S,求:
(1)S与t之间的函数关系式,并写出自变量的取值范围;
(2)当时,求线段PQ的长;
(3)当t为何值时,?
一、单选题
1.D
【分析】本题考查了二次函数的定义.熟练掌握二次函数的定义是解题的关键.
根据二次函数的定义进行判断作答即可.
【详解】解:,是一次函数,故A不符合要求;
,是一次函数,故B不符合要求;
当时,,不是二次函数,故C不符合要求;
,是二次函数,故D符合要求;
故选:D.
2.C
【分析】正方体有6个面,每一个面都是边长为x的正方形,这6个正方形的面积和就是该正方体的表面积.
【详解】解:∵正方体有6个面,每一个面都是边长为x的正方形,
∴表面积.
故选:C.
3.C
【详解】根据二次函数的定义:形如(是常数,且)的函数叫做二次函数.据此可列出关于参数的方程与不等式,求解即可.令,解得或,又,故当时,这个函数是关于的二次函数,故选C.
4.C
【分析】本题考查了列二次函数关系式,正方体有6个面,每个面的面积为据此可求解.
【详解】解:由题意得,,
故选:C.
5.D
【分析】当销售价为元件时,每件利润为元,销售量为,根据利润每件利润销售量列出函数关系式即可.
【详解】解:由题意得,
故选:D.
6.C
【分析】第二季度总值为,第三季度为,得解;
【详解】解:第三季度总值为;
故选:C
7.A
【分析】利用这种产品每天的销售利润等于每千克的销售利润乘以每天的销售量,即可得出w与x之间的函数表达式.
【详解】解:根据题意得,,
即,
故选:A.
8.A
【分析】首先表示出原边长为3的正方形面积,再表示出边长增加x后正方形的面积,再根据面积随之增加y列出方程即可.
【详解】解:原边长为3的正方形面积为:,
边长增加后边长变为:,
则面积为:,
.
故选:A.
9.C
【分析】直接根据二次函数的定义即可得到,计算即可得到答案.
【详解】解:函数的图象是抛物线,
,
,
故选:C.
10.A
【分析】本题考查了等腰直角三角形的性质,矩形的判定和性质,一次函数和二次函数的定义,二次函数求最值.由等腰直角三角形的性质可得,再由,,推出和是等腰直角三角形,四边形是矩形,进而可得y与x的关系,再根据矩形的面积公式可得S与x的关系式,化为顶点式,即可得到最值.
【详解】解:是等腰直角三角形,,
,
,,
和是等腰直角三角形,四边形是矩形,
,,
,
即,
y与x满足一次函数关系,
,最大值为1,
S与x满足二次函数关系,且S存在最大值.
故选:A.
二、填空题
11.②④
【分析】根据二次函数的定义,函数式为整式且自变量的最高次数为2,二次项系数不为0,逐一判断.
【详解】解:①为一次函数;
②为二次函数;
③自变量次数为3,不是二次函数;
④为二次函数;
⑤函数式为分式,不是二次函数.
故答案为②④.
12.
【分析】此题考查了二次函数的定义,根据二次函数的定义:形如,这样的函数叫做二次函数,得到,,进行求解即可.解题的关键是熟练掌握二次函数的定义.
【详解】解:∵函数是二次函数,
∴,,
∴.
故答案为:.
13.二次函数关系
【分析】根据矩形面积公式求出y与x之间的函数关系式即可得到答案.
【详解】解:由题意得,
∴y与x之间的函数关系是二次函数关系,
故答案为;二次函数关系.
14. 5
【分析】根据二次函数的定义判断即可。
【详解】解:二次函数的二次项是,一次项系数是,常数项是,
故答案为:①,② ,③ ,
15.
【分析】由篱笆的总长及一边长度,可得出花圃另一边长为米,再利用矩形的面积公式,即可得出关于的函数解析式.
【详解】解:篱笆的总长为30米,花圃一边长为米,
花圃另一边长为米.
根据题意得:.
故答案为:.
16.
【分析】此题主要考查了根据实际问题抽象出二次函数,掌握二次变化的关系式是解决本题的关键.两年后的产值=本年度的产值增长率,把相关数值代入即可.
【详解】解:第一年度的产值为,
∴第二年度的产值为,
∴.
故答案为:
17.
【分析】本题主要考查二次函数的实际应用,根据题意列出函数整理并求出的取值范围即可.
【详解】解:根据题意,得
展开得:
整理得:
根据题意,得
解得:.
∴y与x之间的函数关系式为,
故答案为:
18.
【分析】本题考查了列二次函数关系式,根据正方形面积等于边长的平方,即可求解.
【详解】解:依题意,,
故答案为:.
三、解答题
19.解:是二次函数,
,解得,
又
.
20.(1)解:∵函数是二次函数,
∴,
解得,,,,,
∴;
(2)解:∵函数是一次函数,
∴,
解得,,,,
∴.
21.(1)解:如图,
∵,
∴,
∴,
∵,
∴,
∴,
∴ ABE∽ ECF,
∴,
∵,,,
∴,
∴,
解得,经检验符合题意.
(2)∵ ABE∽ ECF,
∴,
∵,,,,
∴,
∴
∴,
∴.
22.(1)证明:因为,
所以,
所以不论m为何值,该方程总有两个不相等的实数根.
(2)解:,是原方程的两根,
∴x1+x2=-(m-3),x1x2=1-2m,
∵ +=-2 ,
∴=-2,
∴=-2 ,
解得:,
经检验,是原方程的解,
的值为1;
(3)解:.
因为该函数的图像都会经过一个定点,
所以,
解得,
当时,,
所以该函数图像始终过定点.
23.(1)解:∵篱笆总长为,鸡场的长为,
∴,
故答案为:.
(2)解:,
答:S与的函数关系式为.
(3)解:能围成总面积为的两个长方形养鸡场;
根据题意得:,
解得:,,
∵墙的长度,
∴,
解得:,
∴不符合题意舍去,
∴的长为.
24.解:(1)由条件可得:,,
∴,
∴,;
(2)当时,,,
∴;
(3)由题意可得:,
整理得:,
解得:,,
∴当t为2或3时,.
一、单选题
1.下列各式中,y是x的二次函数的是( )
A. B. C. D.
2.如图,一个正方体的边长为,它的表面积为,则y与x的函数关系式为( )
A. B. C. D.
3.若是关于的二次函数,则的值为( )
A. B.0 C.2 D.
4.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为( )
A. B. C. D.
5.某商店购进某种商品的价格是7.5元/件,在一段时间里,单价是13.5元,销售量是500件,而单价每降低1元就可多售出200件,当销售价为元/件()时,获取利润元,则与的函数关系为( )
A. B.
C. D.以上答案都不对
6.据省统计局公布的数据,合肥市2023年第一季度总值约为2.6千亿元人民币,若我市第三季度总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A. B.
C. D.
7.已知某种产品的成本价为30元/千克,经市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:.设这种产品每天的销售利润为w(元),则w与x之间的函数表达式为( )
A. B.
C. D.
8.正方形的边长为3,若边长增加,则面积增加,与的关系式为( )
A. B.
C. D.
9.函数的图象是抛物线,则实数的取值范围是( )
A. B. C. D.且
10.如图,是等腰直角三角形,,,点为边上一点,过点作,,垂足分别为,,点从点出发沿运动至点.设,,四边形的面积为,在运动过程中,下列说法正确的是( )
A.y与x满足一次函数关系,S与x满足二次函数关系,且S存在最大值
B.y与x满足一次函数关系,S与x满足二次函数关系,且S存在最小值
C.y与x满足反比例函数关系,S与x满足二次函数关系,且S存在最大值
D.y与x满足反比例函数关系,S与x满足二次函数关系,且S存在最小值
二、填空题
11.下列函数①;②;③;④;⑤.其中是二次函数的是 .
12.已知二次函数,则 .
13.如图,矩形绿地的长和宽分别为和.若将该绿地的长、宽各增加,扩充后的绿地的面积为,则y与x之间的函数关系是 .(填“正比例函数关系”、“一次函数关系”或“二次函数关系”)
14.二次函数的二次项是 ,一次项系数是 ,常数项是 .
15.用长为30米的栅栏围成一个矩形花坛,其中一边长为x米,面积为y平方米,则y与x的函数关系为 (不要求写自变量取值范围).
16.某工厂本年度的产值为100万元,若在今后两年里产值的年增长率均为x,两年后的产值为y万元.那么y关于x的函数解析式是 .
17.相框边的宽窄影响可放入相片的大小.如图,相框长,宽,相框边的宽为,相框内的面积是,则y与x之间的函数关系式为 .
18.正方形边长,若边长增加,增加后正方形的面积为,与的函数关系式为 .
三、解答题
19.当为何值时,函数是二次函数.
20.已知函数.
(1)当函数是二次函数时,求的值:
(2)当函数是一次函数时,求的值.
21.如图,,,,射线于点C,E是线段上一点,F是射线上一点,且满足.
(1)若,求的长;
(2)设,,写出y关于x的函数关系式.
22.已知方程(m为常数).
(1)求证:不论m为何值,该方程总有两个不相等的实数根.
(2),是原方程的两根,且,求m的值.
(3)若函数(m为常数)不论m为何值,该函数的图像都会经过一个定点,求定点的坐标.
23.要建如图所示两个长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙长,另外的边用竹篱笆围成,已知篱笆总长为,且在边上开一扇长为的门,在边上开一扇长为的门,若设鸡场的长为.
(1)的长为_____________(用含的代数式表示)
(2)若两个鸡场的总面积为,求S与的函数关系式
(3)能否围成总面积为的两个长方形养鸡场?若能,求出的长;若不能,请说明理由.
24.如图,在中,,,,现有一个动点P从点A出发,以4cm/s的速度沿AC向终点C运动,动点Q同时从点C出发,以2cm/s的速度沿CB向终点B运动,当有一点到达终点时,另一点随之停止运动.设运动时间为ts,的面积为S,求:
(1)S与t之间的函数关系式,并写出自变量的取值范围;
(2)当时,求线段PQ的长;
(3)当t为何值时,?
一、单选题
1.D
【分析】本题考查了二次函数的定义.熟练掌握二次函数的定义是解题的关键.
根据二次函数的定义进行判断作答即可.
【详解】解:,是一次函数,故A不符合要求;
,是一次函数,故B不符合要求;
当时,,不是二次函数,故C不符合要求;
,是二次函数,故D符合要求;
故选:D.
2.C
【分析】正方体有6个面,每一个面都是边长为x的正方形,这6个正方形的面积和就是该正方体的表面积.
【详解】解:∵正方体有6个面,每一个面都是边长为x的正方形,
∴表面积.
故选:C.
3.C
【详解】根据二次函数的定义:形如(是常数,且)的函数叫做二次函数.据此可列出关于参数的方程与不等式,求解即可.令,解得或,又,故当时,这个函数是关于的二次函数,故选C.
4.C
【分析】本题考查了列二次函数关系式,正方体有6个面,每个面的面积为据此可求解.
【详解】解:由题意得,,
故选:C.
5.D
【分析】当销售价为元件时,每件利润为元,销售量为,根据利润每件利润销售量列出函数关系式即可.
【详解】解:由题意得,
故选:D.
6.C
【分析】第二季度总值为,第三季度为,得解;
【详解】解:第三季度总值为;
故选:C
7.A
【分析】利用这种产品每天的销售利润等于每千克的销售利润乘以每天的销售量,即可得出w与x之间的函数表达式.
【详解】解:根据题意得,,
即,
故选:A.
8.A
【分析】首先表示出原边长为3的正方形面积,再表示出边长增加x后正方形的面积,再根据面积随之增加y列出方程即可.
【详解】解:原边长为3的正方形面积为:,
边长增加后边长变为:,
则面积为:,
.
故选:A.
9.C
【分析】直接根据二次函数的定义即可得到,计算即可得到答案.
【详解】解:函数的图象是抛物线,
,
,
故选:C.
10.A
【分析】本题考查了等腰直角三角形的性质,矩形的判定和性质,一次函数和二次函数的定义,二次函数求最值.由等腰直角三角形的性质可得,再由,,推出和是等腰直角三角形,四边形是矩形,进而可得y与x的关系,再根据矩形的面积公式可得S与x的关系式,化为顶点式,即可得到最值.
【详解】解:是等腰直角三角形,,
,
,,
和是等腰直角三角形,四边形是矩形,
,,
,
即,
y与x满足一次函数关系,
,最大值为1,
S与x满足二次函数关系,且S存在最大值.
故选:A.
二、填空题
11.②④
【分析】根据二次函数的定义,函数式为整式且自变量的最高次数为2,二次项系数不为0,逐一判断.
【详解】解:①为一次函数;
②为二次函数;
③自变量次数为3,不是二次函数;
④为二次函数;
⑤函数式为分式,不是二次函数.
故答案为②④.
12.
【分析】此题考查了二次函数的定义,根据二次函数的定义:形如,这样的函数叫做二次函数,得到,,进行求解即可.解题的关键是熟练掌握二次函数的定义.
【详解】解:∵函数是二次函数,
∴,,
∴.
故答案为:.
13.二次函数关系
【分析】根据矩形面积公式求出y与x之间的函数关系式即可得到答案.
【详解】解:由题意得,
∴y与x之间的函数关系是二次函数关系,
故答案为;二次函数关系.
14. 5
【分析】根据二次函数的定义判断即可。
【详解】解:二次函数的二次项是,一次项系数是,常数项是,
故答案为:①,② ,③ ,
15.
【分析】由篱笆的总长及一边长度,可得出花圃另一边长为米,再利用矩形的面积公式,即可得出关于的函数解析式.
【详解】解:篱笆的总长为30米,花圃一边长为米,
花圃另一边长为米.
根据题意得:.
故答案为:.
16.
【分析】此题主要考查了根据实际问题抽象出二次函数,掌握二次变化的关系式是解决本题的关键.两年后的产值=本年度的产值增长率,把相关数值代入即可.
【详解】解:第一年度的产值为,
∴第二年度的产值为,
∴.
故答案为:
17.
【分析】本题主要考查二次函数的实际应用,根据题意列出函数整理并求出的取值范围即可.
【详解】解:根据题意,得
展开得:
整理得:
根据题意,得
解得:.
∴y与x之间的函数关系式为,
故答案为:
18.
【分析】本题考查了列二次函数关系式,根据正方形面积等于边长的平方,即可求解.
【详解】解:依题意,,
故答案为:.
三、解答题
19.解:是二次函数,
,解得,
又
.
20.(1)解:∵函数是二次函数,
∴,
解得,,,,,
∴;
(2)解:∵函数是一次函数,
∴,
解得,,,,
∴.
21.(1)解:如图,
∵,
∴,
∴,
∵,
∴,
∴,
∴ ABE∽ ECF,
∴,
∵,,,
∴,
∴,
解得,经检验符合题意.
(2)∵ ABE∽ ECF,
∴,
∵,,,,
∴,
∴
∴,
∴.
22.(1)证明:因为,
所以,
所以不论m为何值,该方程总有两个不相等的实数根.
(2)解:,是原方程的两根,
∴x1+x2=-(m-3),x1x2=1-2m,
∵ +=-2 ,
∴=-2,
∴=-2 ,
解得:,
经检验,是原方程的解,
的值为1;
(3)解:.
因为该函数的图像都会经过一个定点,
所以,
解得,
当时,,
所以该函数图像始终过定点.
23.(1)解:∵篱笆总长为,鸡场的长为,
∴,
故答案为:.
(2)解:,
答:S与的函数关系式为.
(3)解:能围成总面积为的两个长方形养鸡场;
根据题意得:,
解得:,,
∵墙的长度,
∴,
解得:,
∴不符合题意舍去,
∴的长为.
24.解:(1)由条件可得:,,
∴,
∴,;
(2)当时,,,
∴;
(3)由题意可得:,
整理得:,
解得:,,
∴当t为2或3时,.
