解直角三角形-仰角与俯角
图片预览


文档简介
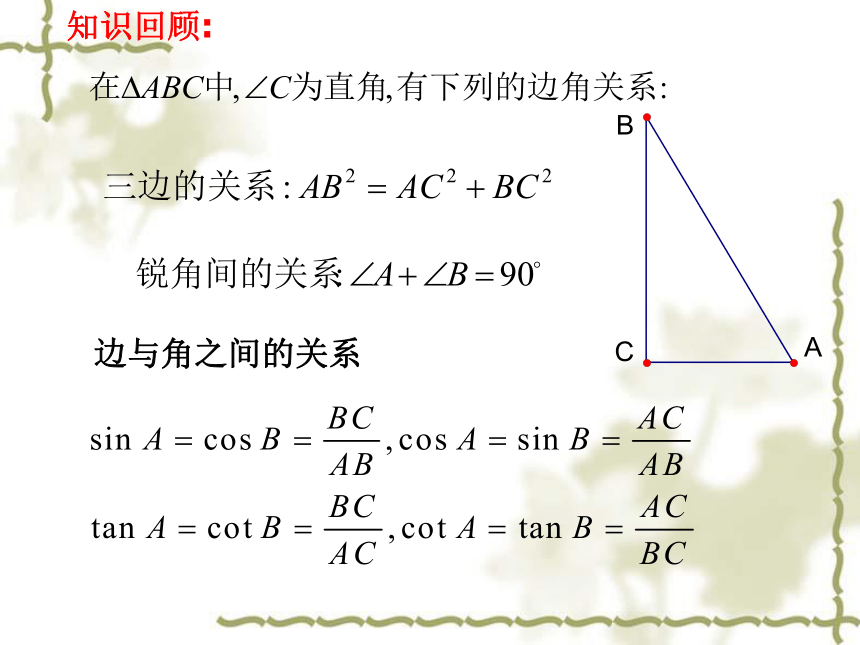
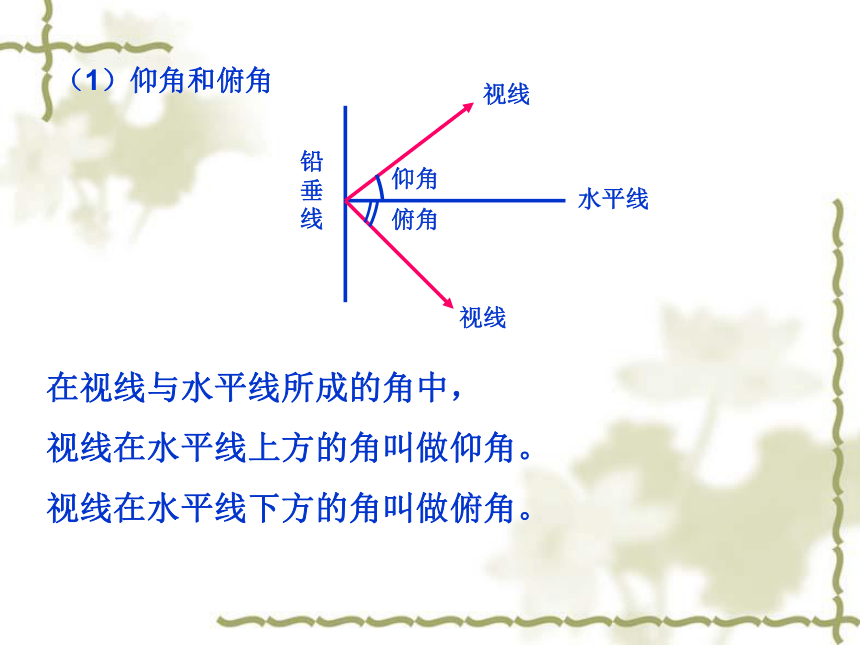
课件21张PPT。知识回顾:边与角之间的关系解直角三角形的应用(一)(1)仰角和俯角铅垂线水平线视线视线在视线与水平线所成的角中,
视线在水平线上方的角叫做仰角。
视线在水平线下方的角叫做俯角。AP铅垂线水平线试问:如果丙在战斗机上的P处看目标A,则图中哪个角是俯角?
DE答:∠DPA、
战斗机·AB 铅垂线水平线水平线试问:
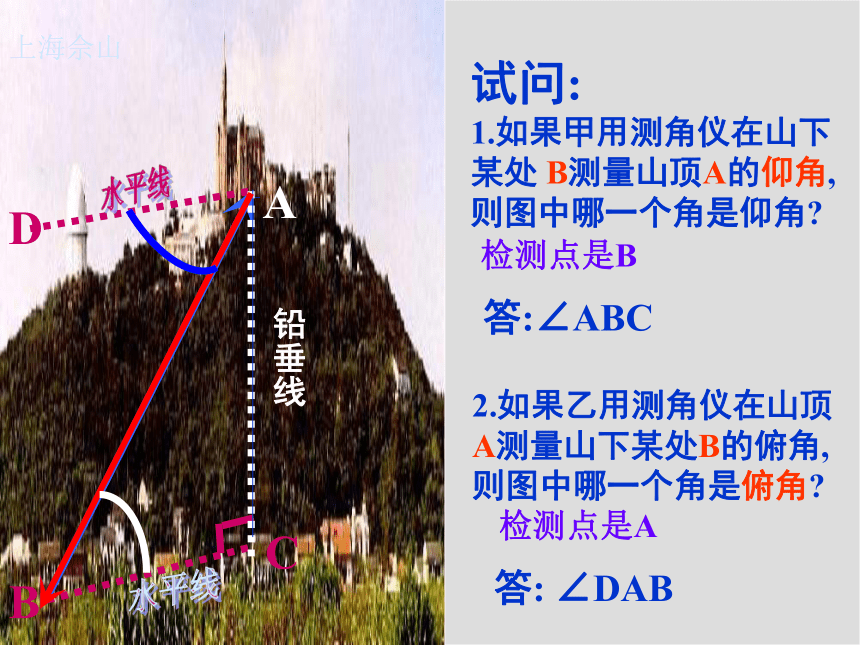
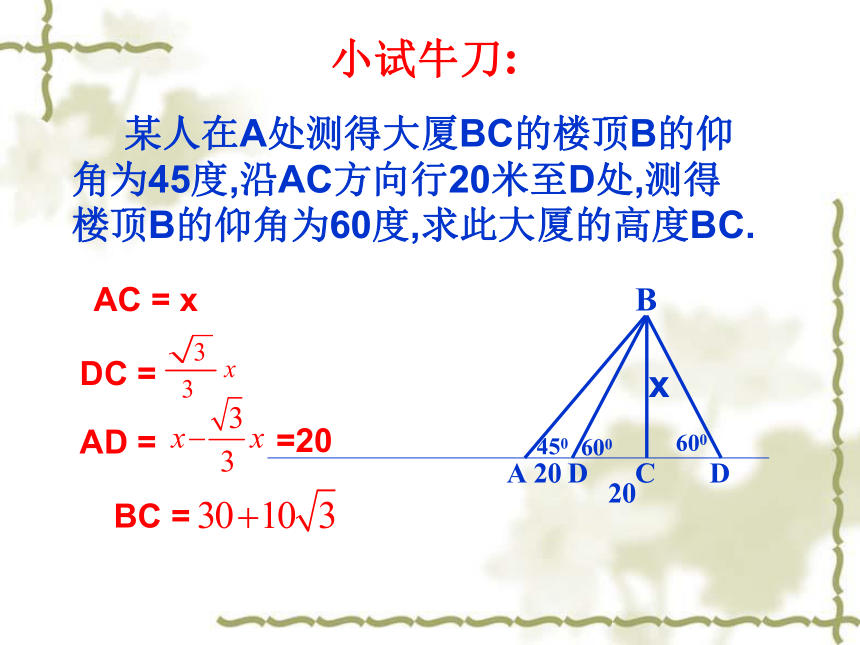
1.如果甲用测角仪在山下某处 B测量山顶A的仰角,则图中哪一个角是仰角?2.如果乙用测角仪在山顶A测量山下某处B的俯角,则图中哪一个角是俯角?答:∠ABC答: ∠DAB上海佘山CD检测点是B检测点是A 某人在A处测得大厦BC的楼顶B的仰角为45度,沿AC方向行20米至D处,测得楼顶B的仰角为60度,求此大厦的高度BC.
AB450600小试牛刀:C
D
20xAC = xDC =D
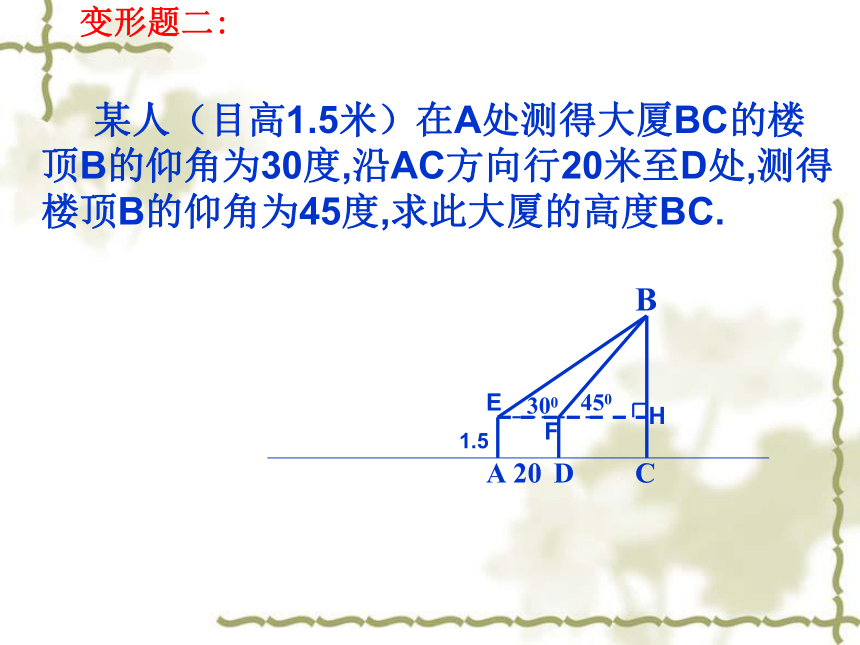
60020AD ==20BC =F 某人(目高1.5米)在A处测得大厦BC的楼顶B的仰角为30度,沿AC方向行20米至D处,测得楼顶B的仰角为45度,求此大厦的高度BC.
AB300450C
D
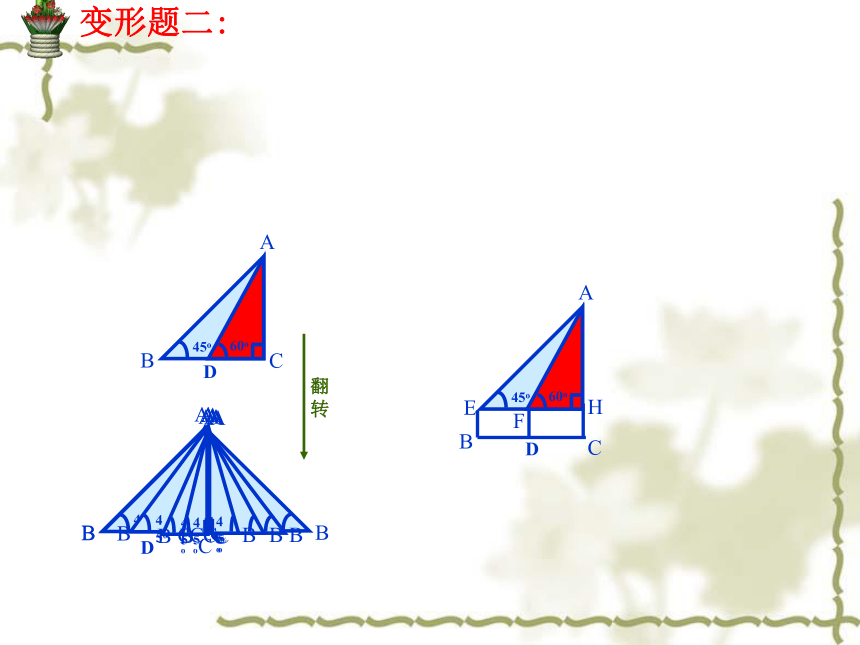
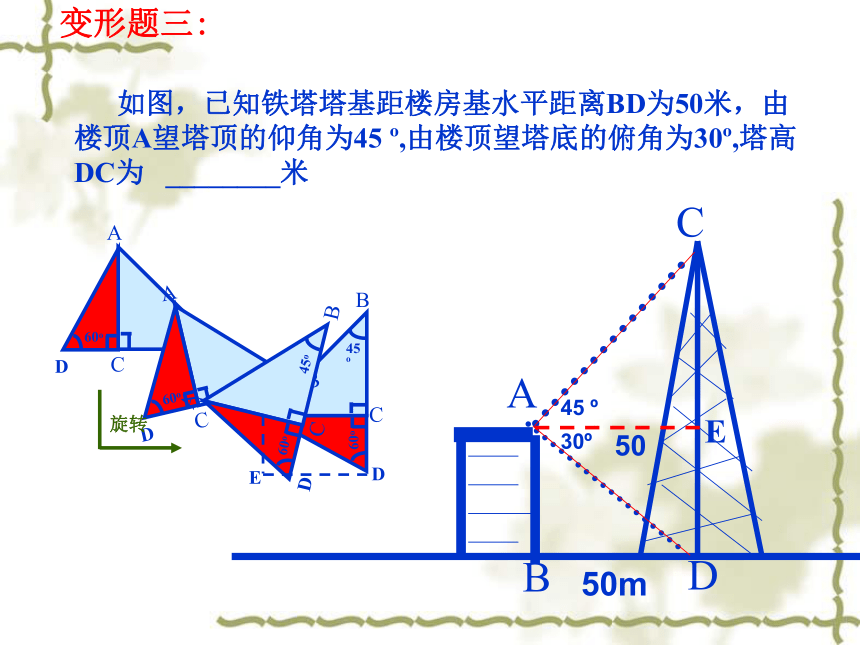
20变形题二:1.5EH变形题二:变形题三:50m45 o30o50变形题四:
D问题1:
楼房BC的高度是多少?问题2:
楼房DA的高度是多少?
从高楼BC的楼顶B看低楼DA的楼顶和楼底的俯角为45°和60°,已知AC=50mHD题后小结:aaααββ基 本 图 形如图:已知角α 、β和边a,求:AB的长。图1图2解:图1 : AB=a·ctgβ– a·ctgα=a(ctgβ– ctgα) 图2: AB=a·ctgβ+ a·ctgα=a(ctgβ+ ctgα) a米例1、直升飞机在长a米的大桥AB的上方P点处,且A、B、O三点在一直线上,在大桥两端A、B测得飞机的仰角分别α、β,求飞机的高度。应用举例:设OP = x在Rt△BOP中,cotβ =在Rt△AOP中,cotα =则 BO = xcotβ,OA = xcotα∵AB = a∴xcot α– xcot β = a∴x = 答:飞机的高度为米.1C300米AB练习1 在山脚C处测得山顶A的仰角为∠1 ,沿着水平地面向前300米到达D点,在D点测得山顶A的仰角为 ∠2,求山高AB。(tg∠1=4/3 , tg∠2=12/5 )
D ∴x=225
∴AB= 4x=900米
答:AB=900米。2解:∵Rt△ABD,
tg ∠1= =∴设AB= 4x米,
CB=3x 米又∵Rt△ABD,tg ∠2 =即练习2、直升飞机在大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一直线上,测得大桥的俯角α=30°,β=45°,求:大桥的长AB。450米Q解:由题意得,∠PBO = 45°,∠PAO = 30 °在Rt△AOP中,cot∠PAO = ∵OP = 450米∴OB = 450米同理OA = 450 米∴AB =练习3、直升飞机在大桥的上方,此时飞机离地面的高度PO=a米,在大桥两端A、B 测得飞机的仰角分别α、β,求大桥的长。
a∵OP = a在Rt△BOP中,cotβ =在Rt△AOP中,cotα =∴OB = acotβ,OA = acotα∴AB = acotα+ acotβ 答:大桥的长为例2.已知如图,塔和楼的水平距离为80米,
从楼顶处及楼底处测得塔顶的仰角分别为
45o和60o,试求塔高与楼高.80E解:过C作CE⊥AB,垂足为E在Rt△ABD中,∠ADB = 60° ∵BD = 80 ∴ AB = 在Rt△AEC中,∠ACE = 45° ∵EC = 80 ∴ AE = 由题意得,EC=BD=80,CD=EB∴ CD = EB = 答:塔高 米,楼高( )米 算一算 为了测量铁塔的高度,在离铁塔330米的C处,用测角仪测得塔顶A的仰角是30°, 已知测角仪的高CD = 1米,求铁塔的高度AB。(精确到0.1米)330mABCDEα︶1mAB = AE + EB≈191.5 米 起重机的机身高20米,吊杆长AB是36米,吊杆的倾角可以从30°转到80°,求这台起重机工作时的最大高度和最大水平距离。(精确到0.1米) (参考数据:sin80°=0.9848,cos80°=0.1736)算一算AC例3、在山脚C处测得山顶A的仰角为45°。问题如下: 沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为60 ° ,求山高AB。DB小结:本节课你学到了什么?①仰角与俯角的概念。②运用解直角三角形的知识解决测距问题。③运用化归及方程思想解决实际问题
视线在水平线上方的角叫做仰角。
视线在水平线下方的角叫做俯角。AP铅垂线水平线试问:如果丙在战斗机上的P处看目标A,则图中哪个角是俯角?
DE答:∠DPA、
战斗机·AB 铅垂线水平线水平线试问:
1.如果甲用测角仪在山下某处 B测量山顶A的仰角,则图中哪一个角是仰角?2.如果乙用测角仪在山顶A测量山下某处B的俯角,则图中哪一个角是俯角?答:∠ABC答: ∠DAB上海佘山CD检测点是B检测点是A 某人在A处测得大厦BC的楼顶B的仰角为45度,沿AC方向行20米至D处,测得楼顶B的仰角为60度,求此大厦的高度BC.
AB450600小试牛刀:C
D
20xAC = xDC =D
60020AD ==20BC =F 某人(目高1.5米)在A处测得大厦BC的楼顶B的仰角为30度,沿AC方向行20米至D处,测得楼顶B的仰角为45度,求此大厦的高度BC.
AB300450C
D
20变形题二:1.5EH变形题二:变形题三:50m45 o30o50变形题四:
D问题1:
楼房BC的高度是多少?问题2:
楼房DA的高度是多少?
从高楼BC的楼顶B看低楼DA的楼顶和楼底的俯角为45°和60°,已知AC=50mHD题后小结:aaααββ基 本 图 形如图:已知角α 、β和边a,求:AB的长。图1图2解:图1 : AB=a·ctgβ– a·ctgα=a(ctgβ– ctgα) 图2: AB=a·ctgβ+ a·ctgα=a(ctgβ+ ctgα) a米例1、直升飞机在长a米的大桥AB的上方P点处,且A、B、O三点在一直线上,在大桥两端A、B测得飞机的仰角分别α、β,求飞机的高度。应用举例:设OP = x在Rt△BOP中,cotβ =在Rt△AOP中,cotα =则 BO = xcotβ,OA = xcotα∵AB = a∴xcot α– xcot β = a∴x = 答:飞机的高度为米.1C300米AB练习1 在山脚C处测得山顶A的仰角为∠1 ,沿着水平地面向前300米到达D点,在D点测得山顶A的仰角为 ∠2,求山高AB。(tg∠1=4/3 , tg∠2=12/5 )
D ∴x=225
∴AB= 4x=900米
答:AB=900米。2解:∵Rt△ABD,
tg ∠1= =∴设AB= 4x米,
CB=3x 米又∵Rt△ABD,tg ∠2 =即练习2、直升飞机在大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一直线上,测得大桥的俯角α=30°,β=45°,求:大桥的长AB。450米Q解:由题意得,∠PBO = 45°,∠PAO = 30 °在Rt△AOP中,cot∠PAO = ∵OP = 450米∴OB = 450米同理OA = 450 米∴AB =练习3、直升飞机在大桥的上方,此时飞机离地面的高度PO=a米,在大桥两端A、B 测得飞机的仰角分别α、β,求大桥的长。
a∵OP = a在Rt△BOP中,cotβ =在Rt△AOP中,cotα =∴OB = acotβ,OA = acotα∴AB = acotα+ acotβ 答:大桥的长为例2.已知如图,塔和楼的水平距离为80米,
从楼顶处及楼底处测得塔顶的仰角分别为
45o和60o,试求塔高与楼高.80E解:过C作CE⊥AB,垂足为E在Rt△ABD中,∠ADB = 60° ∵BD = 80 ∴ AB = 在Rt△AEC中,∠ACE = 45° ∵EC = 80 ∴ AE = 由题意得,EC=BD=80,CD=EB∴ CD = EB = 答:塔高 米,楼高( )米 算一算 为了测量铁塔的高度,在离铁塔330米的C处,用测角仪测得塔顶A的仰角是30°, 已知测角仪的高CD = 1米,求铁塔的高度AB。(精确到0.1米)330mABCDEα︶1mAB = AE + EB≈191.5 米 起重机的机身高20米,吊杆长AB是36米,吊杆的倾角可以从30°转到80°,求这台起重机工作时的最大高度和最大水平距离。(精确到0.1米) (参考数据:sin80°=0.9848,cos80°=0.1736)算一算AC例3、在山脚C处测得山顶A的仰角为45°。问题如下: 沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为60 ° ,求山高AB。DB小结:本节课你学到了什么?①仰角与俯角的概念。②运用解直角三角形的知识解决测距问题。③运用化归及方程思想解决实际问题
