华师大版(2024)数学七下6.2二元一次方程组的解法(第3课时)课件(共20张PPT)
文档属性
| 名称 | 华师大版(2024)数学七下6.2二元一次方程组的解法(第3课时)课件(共20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
(华师大版)七年级
下
6.2二元一次方程组的解法(第3课时)
一次方程组
第6章
“六”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.找出实际问题中的已知量、未知量及这些量之间的等量关系,能够根据等量关系设未知数,列出方程组,利用消元法解方程组.
2.借助二元一次方程组解决简单的实际问题.
新知导入
问题1:解二元一次方程组的基本思路是什么?
二元
一元
消元:
问题2:二元一次方程组解法有哪些?
代入消元法、加减消元法.
新知讲解
例6 某蔬菜公司收购到某种蔬菜140t,准备加工后上市销售。该公司的加工能力是:每天可以粗加工16t或者精加工6t.现计划用15天完成加工任务,该公司应安排几天粗加工,几天精加工 如果每吨蔬菜粗加工后的利润为1000元,精加工后的利润为2000元,那么照此安排,该公司出售这些加工后的蔬菜共可获利多少元
新知讲解
分析:本题的关键是解答第一个问题,即先求出安排粗加工和精加工的天数。从题目的信息中我们可以得到这样的等量关系:
(1)粗加工天数+精加工天数=15;
(2)粗加工任务+精加工任务=140.
设粗加工和精加工的天数分别为x、y,将两个等量关系直接“翻译”就可列出方程组.
新知讲解
解:设应安排x天粗加工,y天精加工,根据题意,得
解这个方程组,得
出售这些加工后的蔬菜一共可获利
1000×16×5+2000×6×10=200 000(元).
答:应安排 5 天粗加工,10 天精加工,加工后出售共可获利 200 000 元.
新知讲解
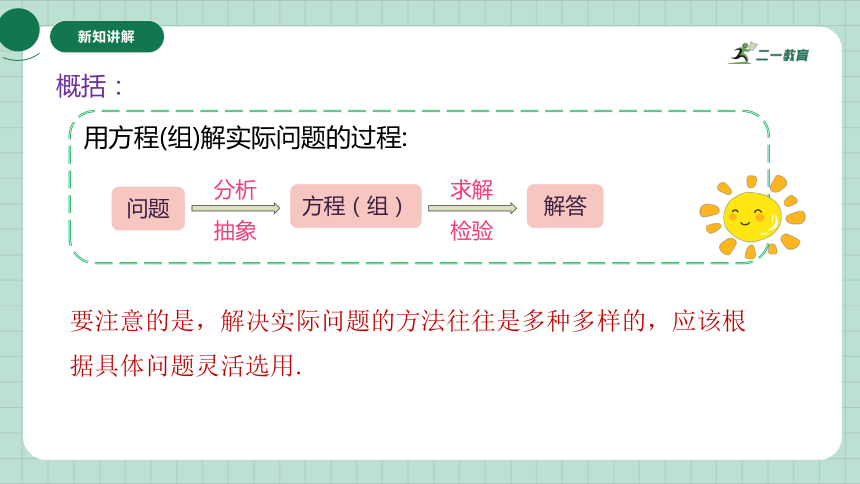
概括:
用方程(组)解实际问题的过程:
要注意的是,解决实际问题的方法往往是多种多样的,应该根据具体问题灵活选用.
问题
方程(组)
分析
抽象
解答
求解
检验
新知讲解
列二元一次方程组解应用题的一般步骤:
可概括为“审、设、列、解、答”五步,即:
(1)审:通过审题,把实际问题抽象成数学问题,分析已知量和未知量,找出能够表示题意的两个相等关系;
(2)设:将两个未知数用字母设出来;
(3)列:根据这两个相等关系列出必需的代数式,从而列出方程组;
(4)解:解这个方程组,求出两个未知数的值;
(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案.
【知识技能类作业】必做题:
课堂练习
1.某地响应国家号召,实施退耕还林政策.退耕还林之前,该地的林地面积和耕地面积共有 .退耕还林之后,该地的耕地面积是林地面积的.设退耕还林之后该地的耕地面积为,林地面积为 ,则可列方程组为( )
A. B. C. D.
B
【知识技能类作业】必做题:
课堂练习
2.学校文艺部组织部分成员观看演出,共购得8张甲种票、4张乙种票,总计用了112元.已知每张甲种票比每张乙种票贵2元,则甲种票、乙种票的票价分别是( )
A. 10元/张、8元/张 B. 11元/张、9元/张
C. 12元/张、10元/张 D. 13元/张、11元/张
A
3.某校七年级的数学竞赛中共有30道题,答对一道题得5分,不答得0分,答错扣4分.学生小王有5道题未答,最后得71分,那么他答对了____道题.
【知识技能类作业】必做题:
课堂练习
19
【知识技能类作业】选做题:
课堂练习
4.小明打算购买5支单价相同的签字笔和3本单价相同的笔记本,期间他与售货员的对话如图所示,则购买1支签字笔和1本笔记本应付( )
A. 10元 B. 11元 C. 12元 D. 13元
C
小明:“您好,我要买5支签字笔和3本笔记本,要付44元吗 ”
售货员:“好的,你应该要付52元.”
小明:“不好意思,刚才我把两种文具的单价弄反了!”
5.甲、乙二人分别从相距20千米的A、B两地出发,相向而行.如果甲比乙早出发半小时,那么乙出发2小时后,他们相遇;如果他们同时出发,那么1小时后两人还相距11千米.甲每小时走 千米,乙每小时走 千米.
【知识技能类作业】选做题:
课堂练习
4
5
【综合拓展类作业】
课堂练习
6. 程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人?请你解决这个问题.
【综合拓展类作业】
课堂练习
解:设小和尚有人,大和尚有 人,
依题意,得解得
答:小和尚有75人,大和尚有25人.
课堂总结
1.用方程(组)解实际问题的过程:
2.列二元一次方程组解应用题的一般步骤:
(1)审;(2)设;(3)列;(4)解;(5)答.
问题
方程(组)
分析
抽象
解答
求解
检验
板书设计
课题:6.2二元一次方程组的解法(第3课时)
1.用方程(组)解实际问题的过程:
2.列二元一次方程组解应用题的一般步骤:
(1)审;(2)设;(3)列;(4)解;(5)答.
问题
方程(组)
分析
抽象
解答
求解
检验
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
6.2二元一次方程组的解法(第3课时)
一次方程组
第6章
“六”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.找出实际问题中的已知量、未知量及这些量之间的等量关系,能够根据等量关系设未知数,列出方程组,利用消元法解方程组.
2.借助二元一次方程组解决简单的实际问题.
新知导入
问题1:解二元一次方程组的基本思路是什么?
二元
一元
消元:
问题2:二元一次方程组解法有哪些?
代入消元法、加减消元法.
新知讲解
例6 某蔬菜公司收购到某种蔬菜140t,准备加工后上市销售。该公司的加工能力是:每天可以粗加工16t或者精加工6t.现计划用15天完成加工任务,该公司应安排几天粗加工,几天精加工 如果每吨蔬菜粗加工后的利润为1000元,精加工后的利润为2000元,那么照此安排,该公司出售这些加工后的蔬菜共可获利多少元
新知讲解
分析:本题的关键是解答第一个问题,即先求出安排粗加工和精加工的天数。从题目的信息中我们可以得到这样的等量关系:
(1)粗加工天数+精加工天数=15;
(2)粗加工任务+精加工任务=140.
设粗加工和精加工的天数分别为x、y,将两个等量关系直接“翻译”就可列出方程组.
新知讲解
解:设应安排x天粗加工,y天精加工,根据题意,得
解这个方程组,得
出售这些加工后的蔬菜一共可获利
1000×16×5+2000×6×10=200 000(元).
答:应安排 5 天粗加工,10 天精加工,加工后出售共可获利 200 000 元.
新知讲解
概括:
用方程(组)解实际问题的过程:
要注意的是,解决实际问题的方法往往是多种多样的,应该根据具体问题灵活选用.
问题
方程(组)
分析
抽象
解答
求解
检验
新知讲解
列二元一次方程组解应用题的一般步骤:
可概括为“审、设、列、解、答”五步,即:
(1)审:通过审题,把实际问题抽象成数学问题,分析已知量和未知量,找出能够表示题意的两个相等关系;
(2)设:将两个未知数用字母设出来;
(3)列:根据这两个相等关系列出必需的代数式,从而列出方程组;
(4)解:解这个方程组,求出两个未知数的值;
(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案.
【知识技能类作业】必做题:
课堂练习
1.某地响应国家号召,实施退耕还林政策.退耕还林之前,该地的林地面积和耕地面积共有 .退耕还林之后,该地的耕地面积是林地面积的.设退耕还林之后该地的耕地面积为,林地面积为 ,则可列方程组为( )
A. B. C. D.
B
【知识技能类作业】必做题:
课堂练习
2.学校文艺部组织部分成员观看演出,共购得8张甲种票、4张乙种票,总计用了112元.已知每张甲种票比每张乙种票贵2元,则甲种票、乙种票的票价分别是( )
A. 10元/张、8元/张 B. 11元/张、9元/张
C. 12元/张、10元/张 D. 13元/张、11元/张
A
3.某校七年级的数学竞赛中共有30道题,答对一道题得5分,不答得0分,答错扣4分.学生小王有5道题未答,最后得71分,那么他答对了____道题.
【知识技能类作业】必做题:
课堂练习
19
【知识技能类作业】选做题:
课堂练习
4.小明打算购买5支单价相同的签字笔和3本单价相同的笔记本,期间他与售货员的对话如图所示,则购买1支签字笔和1本笔记本应付( )
A. 10元 B. 11元 C. 12元 D. 13元
C
小明:“您好,我要买5支签字笔和3本笔记本,要付44元吗 ”
售货员:“好的,你应该要付52元.”
小明:“不好意思,刚才我把两种文具的单价弄反了!”
5.甲、乙二人分别从相距20千米的A、B两地出发,相向而行.如果甲比乙早出发半小时,那么乙出发2小时后,他们相遇;如果他们同时出发,那么1小时后两人还相距11千米.甲每小时走 千米,乙每小时走 千米.
【知识技能类作业】选做题:
课堂练习
4
5
【综合拓展类作业】
课堂练习
6. 程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人?请你解决这个问题.
【综合拓展类作业】
课堂练习
解:设小和尚有人,大和尚有 人,
依题意,得解得
答:小和尚有75人,大和尚有25人.
课堂总结
1.用方程(组)解实际问题的过程:
2.列二元一次方程组解应用题的一般步骤:
(1)审;(2)设;(3)列;(4)解;(5)答.
问题
方程(组)
分析
抽象
解答
求解
检验
板书设计
课题:6.2二元一次方程组的解法(第3课时)
1.用方程(组)解实际问题的过程:
2.列二元一次方程组解应用题的一般步骤:
(1)审;(2)设;(3)列;(4)解;(5)答.
问题
方程(组)
分析
抽象
解答
求解
检验
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
