华师大版(2024)数学七下6.4实践与探索 课件(共26张PPT)
文档属性
| 名称 | 华师大版(2024)数学七下6.4实践与探索 课件(共26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
(华师大版)七年级
下
6.4实践与探索
一次方程组
第6章
“六”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.能够对生活中的实际问题进行数学建模.
2.会用二元一次方程组解决实际问题,并检验解的合理性.
新知导入
问题1:列二元一次方程组解决实际问题的步骤是什么?
审、设、列、解、答.
问题2:列二元一次方程组解决实际问题的关键是什么?
关键是找到等量关系.
要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面.已知每张白卡纸可以做2个侧面,或者做3个底面.如果每个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?
新知讲解
问题1:
请你设计一种分法.
新知讲解
想一想:
1.本题有哪些已知量?
2.要求的问题是什么?
3.可以用什么知识进行解答?
①有白卡纸20张;
②每张白卡纸可以做2个侧面,或者做3个底面;
③每个侧面和2个底面可以做成一个包装盒
用几张白卡纸做侧面,几张白卡纸做底面,侧面与底面刚好配套.
新知讲解
想一想,如果可以将一张白卡纸栽出一个侧面和一个底面,那么,该如何分这些白卡纸,才既能使做出的侧面和底面配套,又能充分利用白卡纸?
新知讲解
解:设用张白卡纸做侧面, 张白卡纸做底面,
由题意,得解得
用8张白卡纸做侧面,共做16个侧面,用11张白卡纸做底面,共做33个底面,所以只能做16个包装盒,且剩余一张白卡纸和一个底面的材料,无法全部利用白卡纸,如果可以将一张白纸裁出一个侧面和一个底面,则共可以做出17个侧面和34个底面,正好配套成17个包装盒,较充分地利用了白卡纸.
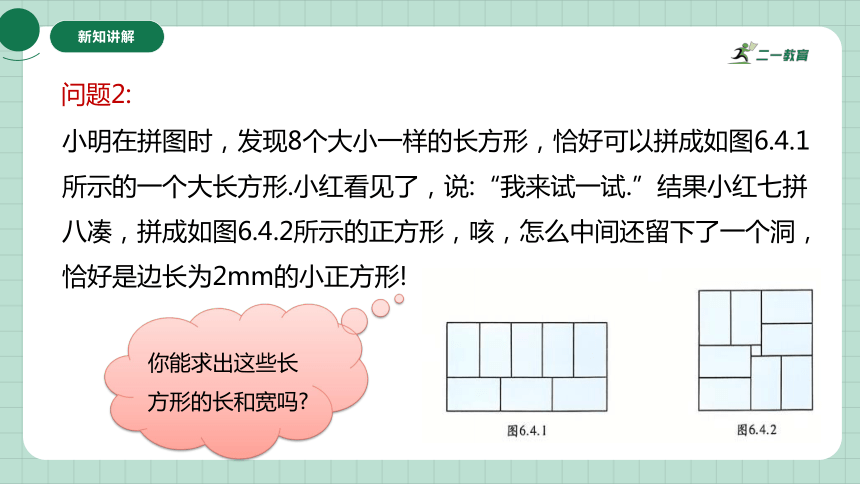
小明在拼图时,发现8个大小一样的长方形,恰好可以拼成如图6.4.1所示的一个大长方形.小红看见了,说:“我来试一试.”结果小红七拼八凑,拼成如图6.4.2所示的正方形,咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!
新知讲解
问题2:
你能求出这些长方形的长和宽吗
新知讲解
探索:
设长方形的长和宽分别为 x mm、y mm.
S大正方形 - 8×S长方形 = 22,
即 (x + 2y)2 - 8xy = 4 .
这是我们还没有研究过的方程! 你有其他办法来解决这个问题吗?
解:设长方形的长和宽分别为 x mm、y mm.
由题意,得
解得
答:长方形的长为10 mm,
宽为6 mm.
新知讲解
在5.3节提出的问题中选出一个,用本章的方法来处理,并比较一下两种方法,谈谈你的感受.
新知讲解
做一做:
5.3问题1(2)
用一根长60 cm的铁丝围成一个长方形.
(2)如果长方形的宽比长少4 cm,求这个长方形的面积.
解:设长方形的长为x cm,宽为y cm.
根据题意,有
解得
17×13=221(cm2)
答:这个长方形的面积为221 cm2.
新知讲解
列方程(组)解决实际问题的一般步骤:
1.审:审题,弄清题意及题目中已知量,未知量;
2.设:设未知数,可直接设元,也可间接设元;
3.找:找出题目中的等量关系;
4.列:根据题目中的等量关系列出方程(组)
5.解:解所列的方程(组);
6.检:检验解的正确性,检验所求未知数是否符合题意;
7.答:写出答语.
【知识技能类作业】必做题:
课堂练习
1.某机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个.已知2个大齿轮与3个小齿轮配成一套.若要使每天加工的大、小齿轮刚好配套,则安排加工大齿轮的工人有( )
A. 20名 B. 25名
C. 48名 D. 60名
B
【知识技能类作业】必做题:
课堂练习
2.某出租车起步价所包含的路程为,超过 的部分另收费.小江乘坐这种出租车走了 ,付了16元;小北乘坐这种出租车走了,付了28元.设这种出租车的起步价为元,超过 后每千米收费 元.根据题意,可列方程组为
___________________.
3.某地居民生活用电基本价格为0.50元/千瓦时,规定每月基本用电量为 千瓦时,超过部分的电量每千瓦时电价比基本用电量的每千瓦时电价增加收费.某用户在5月份用电120千瓦时,共交电费66元,则 ____,超过部分的用电量为____千瓦时.
【知识技能类作业】必做题:
课堂练习
60
60
【知识技能类作业】选做题:
课堂练习
4.如图,把7个相同的小长方形放入大长方形中,则此大长方形的面积是 ( )
A. 60 B. 84
C. 108 D. 132
C
【知识技能类作业】选做题:
课堂练习
5. 某车间有82名工人生产甲、乙两种零件,每人每天平均能生产甲种零件12个或乙种零件25个.已知3个甲种零件和4个乙种零件配成一套,则分配 名工人生产甲种零件, 名工人生产乙种零件,才能使每天生产的这两种零件刚好配套,恰好可以配成 套.
50
32
200
【综合拓展类作业】
课堂练习
6. 某铁件加工厂用如图①所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图②所示的竖式与横式两种无盖的长方体铁容器(加工时接缝材料不计).
(1) 若加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片
张,正方形铁片 张.
7
3
【综合拓展类作业】
课堂练习
(2) 现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,铁片刚好全部用完,那么加工的竖式铁容器、横式铁容器分别有多少个
解:(2) 设加工的竖式铁容器有x个,横式铁容器有y个.根据题意,得解得∴ 加工的竖式铁容器有100个,横式铁容器有538个
【综合拓展类作业】
课堂练习
(3) 把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成与图①相同的长方形铁片和正方形铁片,已知每张铁板可做成3张长方形铁片或4张正方形铁片,也可以做成1张长方形铁片和2张正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒
【综合拓展类作业】
课堂练习
解:(3) 设m张铁板做成长方形铁片,n张铁板做成正方形铁片.
根据题意,得解得
∵ 在这35张铁板中,25张铁板可做长方形铁片25×3=75(张),9张铁板可做正方形铁片9×4=36(张),剩1张可做成1张长方形铁片和2张正方形铁片,∴ 共可做长方形铁片75+1=76(张),正方形铁片36+2=38(张),76÷4=19(个),38÷2=19(个).
∴ 最多可以加工成19个铁盒
课堂总结
列方程(组)解决实际问题的一般步骤:
1.审:审题,弄清题意及题目中已知量,未知量;
2.设:设未知数,可直接设元,也可间接设元;
3.找:找出题目中的等量关系;
4.列:根据题目中的等量关系列出方程(组)
5.解:解所列的方程(组);
6.检:检验解的正确性,检验所求未知数是否符合题意;
7.答:写出答语.
板书设计
列方程(组)解决实际问题的一般步骤:
1.审;2.设;3.找;4.列;5.解;6.检;7.答.
课题:6.4实践与探索
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
6.4实践与探索
一次方程组
第6章
“六”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.能够对生活中的实际问题进行数学建模.
2.会用二元一次方程组解决实际问题,并检验解的合理性.
新知导入
问题1:列二元一次方程组解决实际问题的步骤是什么?
审、设、列、解、答.
问题2:列二元一次方程组解决实际问题的关键是什么?
关键是找到等量关系.
要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面.已知每张白卡纸可以做2个侧面,或者做3个底面.如果每个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?
新知讲解
问题1:
请你设计一种分法.
新知讲解
想一想:
1.本题有哪些已知量?
2.要求的问题是什么?
3.可以用什么知识进行解答?
①有白卡纸20张;
②每张白卡纸可以做2个侧面,或者做3个底面;
③每个侧面和2个底面可以做成一个包装盒
用几张白卡纸做侧面,几张白卡纸做底面,侧面与底面刚好配套.
新知讲解
想一想,如果可以将一张白卡纸栽出一个侧面和一个底面,那么,该如何分这些白卡纸,才既能使做出的侧面和底面配套,又能充分利用白卡纸?
新知讲解
解:设用张白卡纸做侧面, 张白卡纸做底面,
由题意,得解得
用8张白卡纸做侧面,共做16个侧面,用11张白卡纸做底面,共做33个底面,所以只能做16个包装盒,且剩余一张白卡纸和一个底面的材料,无法全部利用白卡纸,如果可以将一张白纸裁出一个侧面和一个底面,则共可以做出17个侧面和34个底面,正好配套成17个包装盒,较充分地利用了白卡纸.
小明在拼图时,发现8个大小一样的长方形,恰好可以拼成如图6.4.1所示的一个大长方形.小红看见了,说:“我来试一试.”结果小红七拼八凑,拼成如图6.4.2所示的正方形,咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!
新知讲解
问题2:
你能求出这些长方形的长和宽吗
新知讲解
探索:
设长方形的长和宽分别为 x mm、y mm.
S大正方形 - 8×S长方形 = 22,
即 (x + 2y)2 - 8xy = 4 .
这是我们还没有研究过的方程! 你有其他办法来解决这个问题吗?
解:设长方形的长和宽分别为 x mm、y mm.
由题意,得
解得
答:长方形的长为10 mm,
宽为6 mm.
新知讲解
在5.3节提出的问题中选出一个,用本章的方法来处理,并比较一下两种方法,谈谈你的感受.
新知讲解
做一做:
5.3问题1(2)
用一根长60 cm的铁丝围成一个长方形.
(2)如果长方形的宽比长少4 cm,求这个长方形的面积.
解:设长方形的长为x cm,宽为y cm.
根据题意,有
解得
17×13=221(cm2)
答:这个长方形的面积为221 cm2.
新知讲解
列方程(组)解决实际问题的一般步骤:
1.审:审题,弄清题意及题目中已知量,未知量;
2.设:设未知数,可直接设元,也可间接设元;
3.找:找出题目中的等量关系;
4.列:根据题目中的等量关系列出方程(组)
5.解:解所列的方程(组);
6.检:检验解的正确性,检验所求未知数是否符合题意;
7.答:写出答语.
【知识技能类作业】必做题:
课堂练习
1.某机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个.已知2个大齿轮与3个小齿轮配成一套.若要使每天加工的大、小齿轮刚好配套,则安排加工大齿轮的工人有( )
A. 20名 B. 25名
C. 48名 D. 60名
B
【知识技能类作业】必做题:
课堂练习
2.某出租车起步价所包含的路程为,超过 的部分另收费.小江乘坐这种出租车走了 ,付了16元;小北乘坐这种出租车走了,付了28元.设这种出租车的起步价为元,超过 后每千米收费 元.根据题意,可列方程组为
___________________.
3.某地居民生活用电基本价格为0.50元/千瓦时,规定每月基本用电量为 千瓦时,超过部分的电量每千瓦时电价比基本用电量的每千瓦时电价增加收费.某用户在5月份用电120千瓦时,共交电费66元,则 ____,超过部分的用电量为____千瓦时.
【知识技能类作业】必做题:
课堂练习
60
60
【知识技能类作业】选做题:
课堂练习
4.如图,把7个相同的小长方形放入大长方形中,则此大长方形的面积是 ( )
A. 60 B. 84
C. 108 D. 132
C
【知识技能类作业】选做题:
课堂练习
5. 某车间有82名工人生产甲、乙两种零件,每人每天平均能生产甲种零件12个或乙种零件25个.已知3个甲种零件和4个乙种零件配成一套,则分配 名工人生产甲种零件, 名工人生产乙种零件,才能使每天生产的这两种零件刚好配套,恰好可以配成 套.
50
32
200
【综合拓展类作业】
课堂练习
6. 某铁件加工厂用如图①所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图②所示的竖式与横式两种无盖的长方体铁容器(加工时接缝材料不计).
(1) 若加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片
张,正方形铁片 张.
7
3
【综合拓展类作业】
课堂练习
(2) 现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,铁片刚好全部用完,那么加工的竖式铁容器、横式铁容器分别有多少个
解:(2) 设加工的竖式铁容器有x个,横式铁容器有y个.根据题意,得解得∴ 加工的竖式铁容器有100个,横式铁容器有538个
【综合拓展类作业】
课堂练习
(3) 把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成与图①相同的长方形铁片和正方形铁片,已知每张铁板可做成3张长方形铁片或4张正方形铁片,也可以做成1张长方形铁片和2张正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒
【综合拓展类作业】
课堂练习
解:(3) 设m张铁板做成长方形铁片,n张铁板做成正方形铁片.
根据题意,得解得
∵ 在这35张铁板中,25张铁板可做长方形铁片25×3=75(张),9张铁板可做正方形铁片9×4=36(张),剩1张可做成1张长方形铁片和2张正方形铁片,∴ 共可做长方形铁片75+1=76(张),正方形铁片36+2=38(张),76÷4=19(个),38÷2=19(个).
∴ 最多可以加工成19个铁盒
课堂总结
列方程(组)解决实际问题的一般步骤:
1.审:审题,弄清题意及题目中已知量,未知量;
2.设:设未知数,可直接设元,也可间接设元;
3.找:找出题目中的等量关系;
4.列:根据题目中的等量关系列出方程(组)
5.解:解所列的方程(组);
6.检:检验解的正确性,检验所求未知数是否符合题意;
7.答:写出答语.
板书设计
列方程(组)解决实际问题的一般步骤:
1.审;2.设;3.找;4.列;5.解;6.检;7.答.
课题:6.4实践与探索
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
