全等三角形复习题
图片预览




文档简介
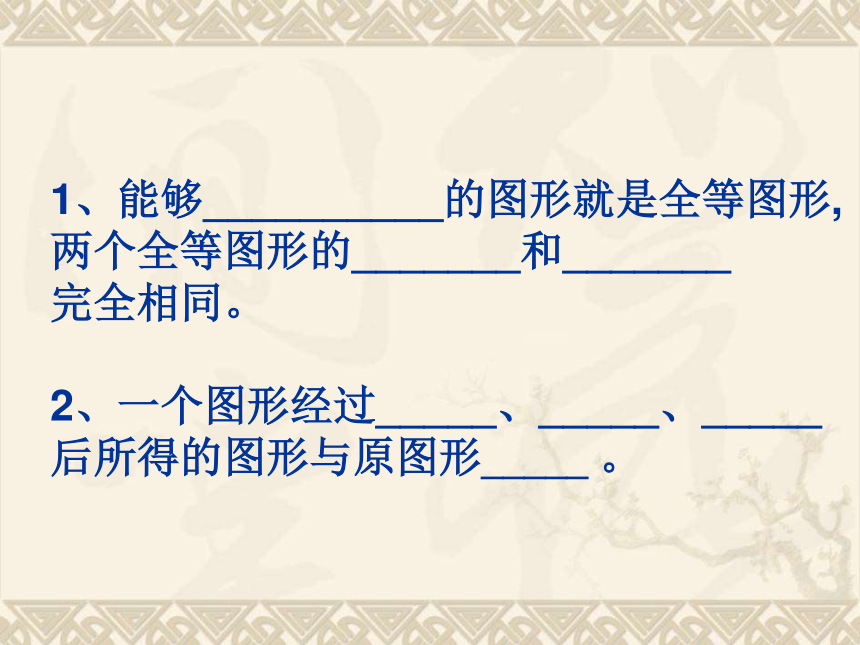
课件49张PPT。全等三角形复习(一)1、能够__________的图形就是全等图形,
两个全等图形的_______和_______
完全相同。
2、一个图形经过_____、_____、_____
后所得的图形与原图形_____ 。3、把两个全等的三角形重合在一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。
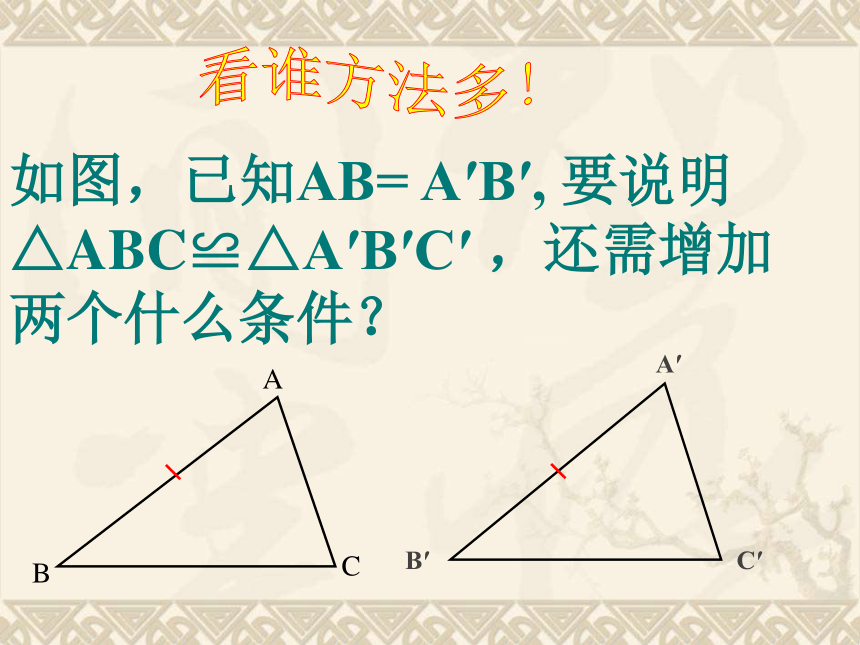
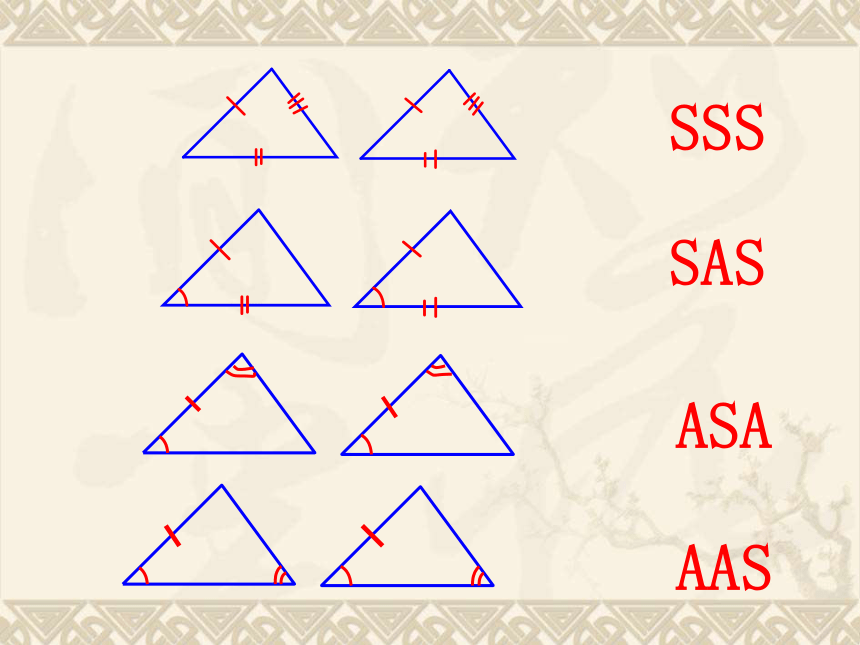
4、全等三角形有这样的性质:全等三角形的 相等, 相等。三角形全等的条件:①一般三角形全等的条件:SAS、ASA、AAS、SSS②直角三角形全等的条件: SAS、ASA、AAS、SSS、HL知识点如图,已知AB= A′B′, 要说明△ABC≌△A′B′C′ ,还需增加两个什么条件?
?
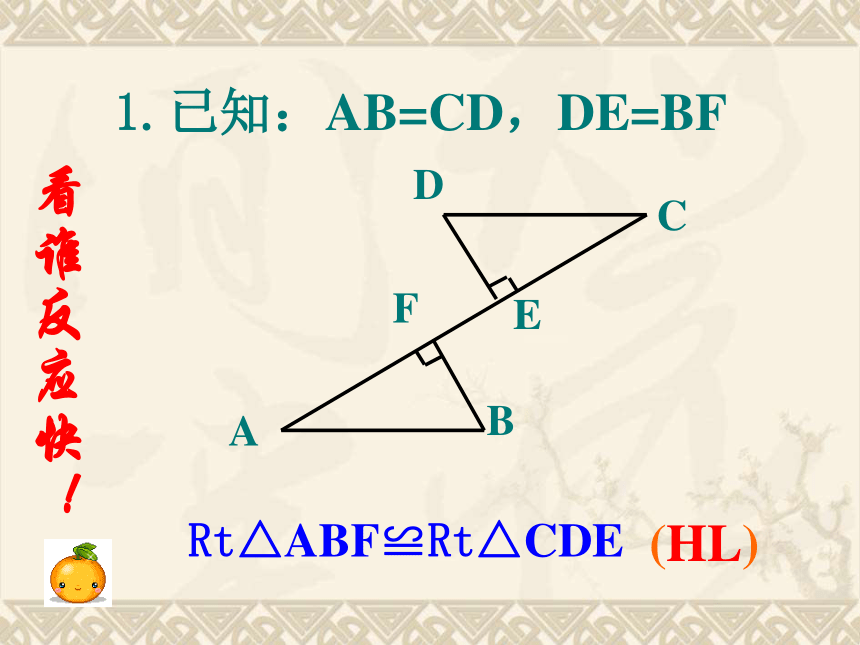
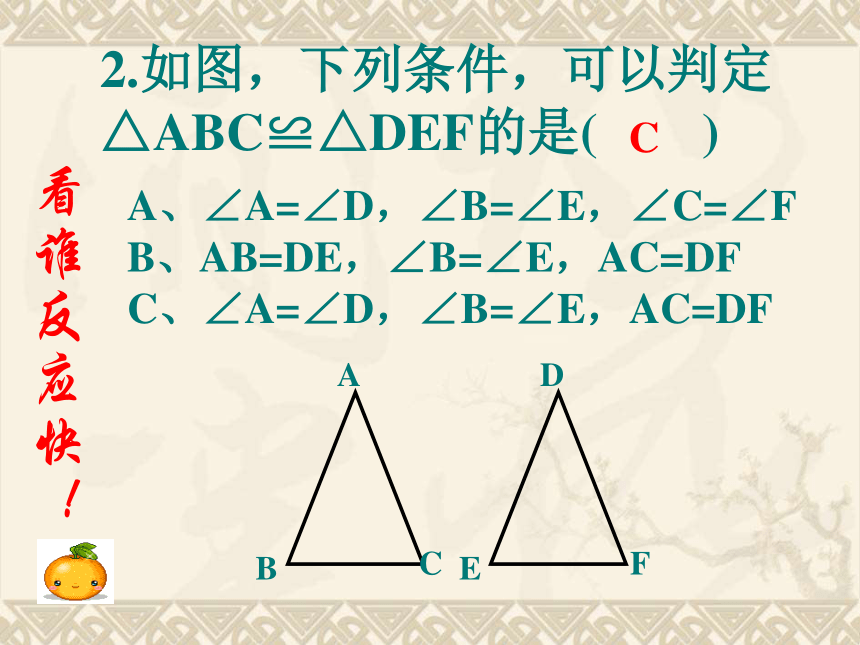
A′C′B′CBA看谁方法多!SSSSASASAAAS1.已知:AB=CD,DE=BF (HL) Rt△ABF≌Rt△CDE 看谁反应快!2.如图,下列条件,可以判定△ABC≌△DEF的是( )C A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
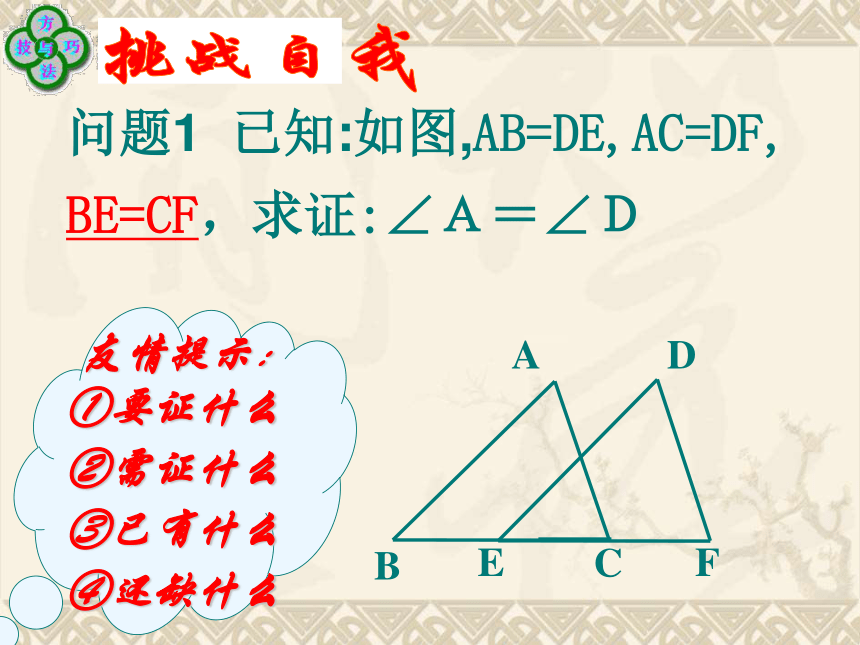
C、∠A=∠D,∠B=∠E,AC=DF 看谁反应快!问题1 已知:如图,AB=DE,AC=DF,
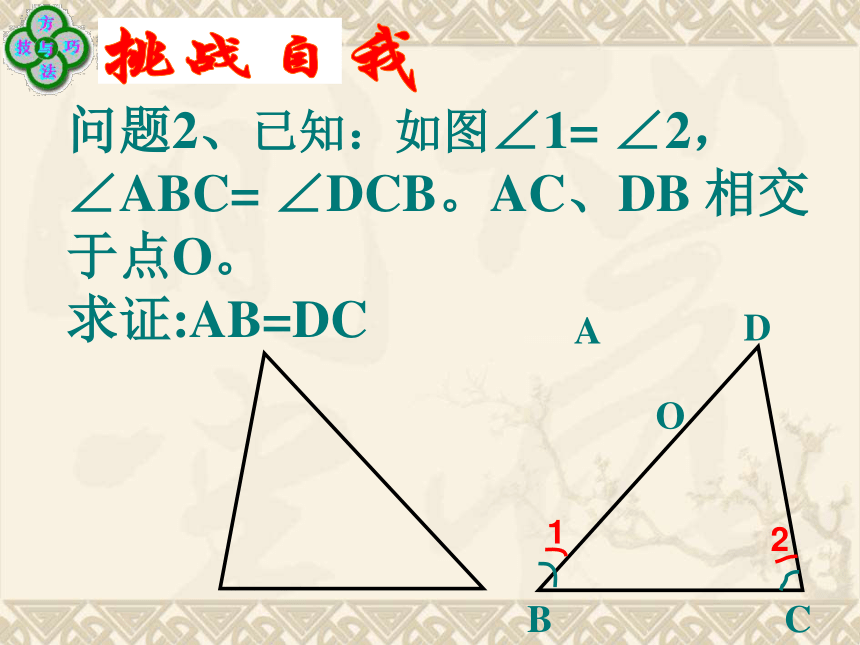
BE=CF,求证:∠A=∠D问题2、已知:如图∠1= ∠2, ∠ABC= ∠DCB。AC、DB 相交于点O。
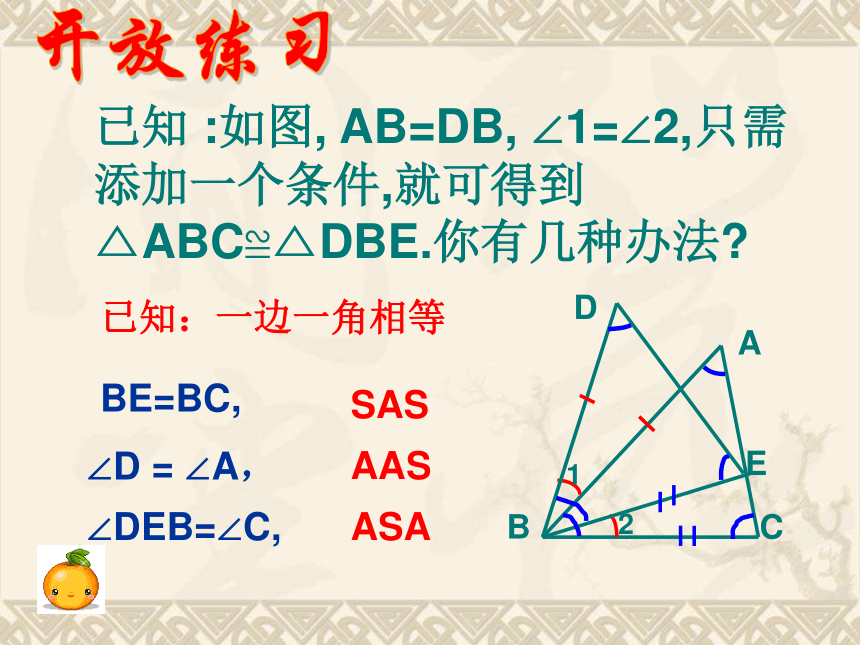
求证:AB=DCABCDO已知 :如图, AB=DB, ∠1=∠2,只需添加一个条件,就可得到△ABC≌△DBE.你有几种办法?开放练习已知:一边一角相等∠D = ∠A,AAS∠DEB=∠C,BE=BC,SASASA1.下列判断中错误的有 (写序号)
①有两角和一边对应相等的两个三角形全等
②有两边和一角对应相等的两个三角形全等
③有两边和其中一边上的中线对应相等的两个三角形全等
④有一边对应相等的两个等边三角形全等
⑤有两边对应相等的两个直角三角形全等
⑥有三个角对应相等的两个三角形全等②、⑥考查知识点:全等三角形的判定方法(SSS)(SAS)(AAS)(ASA)(HL)注意点:看清文字表述2.△ABC和△A′B′C′中,下列各组条件中,不能保证:△ABC≌△A′B′C的是( )
①AB=A′B′; ② BC=B′C′; ③ AC=A′C′
④∠A =∠A′; ⑤∠B =∠B′; ⑥∠C =∠C′
具备① ② ③ B.具备① ② ④
C.具备③④ ⑤ D.具备② ③ ⑥BSSSSSAAASSAS3、如果两个三角形中两条边和其中一边上的高对应
相等,那么这两个三角形的其中有一对
角有什么关系吗?那么这两个三角形全等吗?如果两个三角形中两条边和第三边上的高对应
相等,那么这两个三角形全等吗?相等或互补4.如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,且AO平分∠BAC,则图中全等三角形共有________对。5.如图,已知:AB∥CD,AD ∥BC,OE=OF,则图中全等三角形的组数是( )
A.3 B.4 C.5 D.6解题方法:1、全等三角形的判定方法2、基本图形:平移、对称、旋转3、有规律找:一个、二个、三个4D6.如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出______个。47.用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )
SSS B.SAS C.ASA D.AASA8、得到“角平分线上的点到角两边的距离相等”
的结论,他的依据是( )
A、SSS B、HL C、SAS D、ASA9、得到“到角两边的距离相等的点在这个角的平分线上”
的结论,他的依据是( )
A、SSS B、HL C、SAS D、AASB到三角形三边距离距离相等的点,则可供选择的地址有( )
一处 B.二处 C.三处 D.四处到三角形三边距离距离相等的点是三角形 ( )
A、三条中线的交点 B、三条高线的交点
C、三条角平分线的交点 D、三边垂直平分线的交点10.如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
一处 B.二处 C.三处 D.四处D考查知识点:角平分线上的点到角两
边的距离相等注意点:1、三条公路是直线2、包括三个外角的平分线AC区别题:11.仅用一块没有刻度的直角三角板能画出一个角的平公线吗?
小刚想出了这样的办法:先将直角三角板的一个锐角顶点和∠AOB的顶点O重合,直角边l与OA重合,沿直角边2画出直线l1;再将三角板的同一锐角顶点与O重合,直角边l与OB重合,直角边2画出直线l2,l1与l2交于点P,连接OP并延长,则OP为∠AOB的平分线,你认为小刚的方法正确吗?为什么?回顾画角平分线的方法:12.如图,已知BQ是∠ABC的平分线,CQ是△ABC的外角平分线,由点Q出发,作点Q到BC、AC和AB的垂线段QM、QN和QK,垂足分别是M、N、K,则QM、QN、QK的关系是___________QM=QN=QKQM=QN的理由是QM=QK的理由是(CQ是角平分线)(BQ是角平分线)全等三角形复习(二)全等三角形画法应用已知一个三角形的两边长
分别是1cm和2cm,一个内角为400,
(1)请你借助图形画出一个满足条件的三角形;(2)你是否还能画出既满足已知条件,以现(1)不全的三角形?若能,请你在图用“尺规作图”,若不能,请说明理由.40全等三角形证明1.已知△ABC中,∠C=900,沿BE折叠这个三角形,使点C与D重合,如图,要使D恰为AB的中点,还应添加一个什么条件?(请写出三种答案)
选择(1)中的某一个添加条件作为题目的补充条件 试说明其能使D为AB中点的理由.
解: (1)添加条件:
① ② ③ .
(2)说明:∠A=300∠B=600AB=2BC注意:折叠就有全等全等三角形应用如图,一块三角形模具的阴影部
分已破损,只要从残留的模具片中度量出
哪些角,边,就可以不带残留的模具片到
店铺加工一块与原来的模具ABC的形状
和大小完全相同的模具DEF,请简要说明理由.分析:能确定一个三角形条件 的一块解:只要度量白色残留的一块中的∠B,∠C的度数和边BC的长.理由:因为两角及其夹边对应相等的两个三角形全等请欣赏答题过程2.八年级某班同学到野外上数学活动课,为测量池塘两端A,B的距离,设计如下方案.
方案一:如图1,先在平地上取一个可直接到达A,B的点C,连接AC,BC,并分别延长AC,BC至D,E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长.
方案二:
如图2,先过B作AB垂线BF,再在BF上取C,D两点,使CD=BC,接着过点D作BD的垂线DE,交AC的延长线于点E,测出DE的长即为AB的距离.
阅读后回答下列问题:
(1)方案一判定三角形全等的依据是 .
(2)方案二判定三角形全等的依据是 .
(3)方案二中作BF⊥AB,ED⊥BF的目的是 .
若仅满足∠ABD=∠BDF≠900,方案二是否成立?SASASA∠ABC=∠EDC成立请学会方案设计特别是语言描述方案一方案二全等三角形应用中的典型类问题1.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置有怎样的关系?并证明你的结论。典型在哪里?1.垂直中利用互余证角相等2.求证中的CE与DE的关系是指大小与位置关系.2.如图,已知AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD。求证:BE⊥AC证明:∵ AD为△ABC的高
∴ ∠ADB=∠ADC=90°,∠FBC+ ∠BFD=90°.
在RtΔBDF和RtΔADC中
BF=AC
DE=DC
∴ ∠BFD=∠C, ∴ ∠ FBC +∠C=90°
∴ BE⊥AC{3.如图,BD是∠ABC的角平分线,
DE⊥AB于点E,DF⊥BC于点F,
,AB=18cm,BC=12cm,
求DE的长。利用三角形面积求解全等三角形综合训练 下列说法中不正确的是 ( )
A.全等三角形的对应高相等
B.全等三角形的面积相等
C.全等三角形的周长相等
D.周长相等的两个三角形全等1、B2、已知:△ABC≌△DEF,AC∥DF,
BC∥EF.则不正确的等式是( )
A.AC=DF B.AD=BE
C.DF=EF D.BC=EFA3、下列判断中错误的是( )
A、有两角和一边对应相等的两个三角形全等
B、有两边和一角对应相等的两个三角形全等
C、有两边和其中一边上的中线对应相等的两
个三角形全等
D、有一边对应相等的两个等边三角形全等A4、如图3,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A、带①去
B、带②去
C、带③去
D、带①和②去 C12、下列说法中:
(1)如果两个三角形可以用“AAS”来判定全等,那么
一定可以用“ASA”来判定它们全等;
(2)如果两个三角形都与第三个三角形不全等,那么
这两个三角形也一定不全等;
(3)要判断两个三角形全等,给出的条件中至少要有
一边对应相等。其中正确的是( )
A、(1)和(2) B、(2)和(3)
C、(1)和(3) D、(1)(2)(3)A1.如图,D在AB上,E在
AC上,AB=AC, ∠B=∠C.
求证:AD=AE2.如图,△ABF≌△CDE,
∠B=30°, ∠BAE=∠DCF=20°,
求∠EFC的度数。3.已知:如图,点B,E,C,F在
同一直线上,AB∥DE,且
AB=DE,BE=CF.
求证:AC∥DF. 4.已知:如图12,AB=CD,
DE⊥AC,BF⊥AC,
E,F是垂足,DE=BF.
求证:(1)AF=CE
(2)AB∥CD.
利用三角形全等测距离 在一次战役中,我军阵地与敌军碉堡隔河相望。为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离。在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢?确定碉堡位置 一位战士想出来这样一个办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部.然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上.接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.1212解:在△ADB与△ADC中,有∴△ADB≌△ADC (ASA) .∴DB=DC (全等三角形对应边相等).做一做 在课后,按这个战士的方法,找出教室或操场上与你距离相等的两个点,(想一想,如何才能使得估测尽可能准确?)并通过测量加以验证.想一想例1 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,你能帮他想个办法吗? 一个叔叔帮小明出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.证明:
在△CED与△CBA中,∴DE=AB (全等三角形对应边相等).∴△CED≌△CBA(SAS)例2 如图,太阳光线AC与A’C’是平行的,同一时刻两根高度相同的直立于地上的木杆在太阳光照射下的影子一样长吗?说说理由?证明:∵AC∥A’C’,∴∠ACB=∠A’C’B’在△ABC和△A’B’C’中,有∴△ABC≌△A’B’C’(AAS). 你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗? 例3: 证明:连结DC、D’C’.在△DOC和△D’O’C’中,有∴△DOC≌△D’O’C’(SSS).∴∠DOC=∠D’O’C’ (全等三角形对应角相等).
某城市搞亮化工程,如图,在甲楼底部、乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角是相等的,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.挑战感悟与反思1、本节课你有什么收获?
2 、你有什么感受?再见
两个全等图形的_______和_______
完全相同。
2、一个图形经过_____、_____、_____
后所得的图形与原图形_____ 。3、把两个全等的三角形重合在一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。
4、全等三角形有这样的性质:全等三角形的 相等, 相等。三角形全等的条件:①一般三角形全等的条件:SAS、ASA、AAS、SSS②直角三角形全等的条件: SAS、ASA、AAS、SSS、HL知识点如图,已知AB= A′B′, 要说明△ABC≌△A′B′C′ ,还需增加两个什么条件?
?
A′C′B′CBA看谁方法多!SSSSASASAAAS1.已知:AB=CD,DE=BF (HL) Rt△ABF≌Rt△CDE 看谁反应快!2.如图,下列条件,可以判定△ABC≌△DEF的是( )C A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,AC=DF 看谁反应快!问题1 已知:如图,AB=DE,AC=DF,
BE=CF,求证:∠A=∠D问题2、已知:如图∠1= ∠2, ∠ABC= ∠DCB。AC、DB 相交于点O。
求证:AB=DCABCDO已知 :如图, AB=DB, ∠1=∠2,只需添加一个条件,就可得到△ABC≌△DBE.你有几种办法?开放练习已知:一边一角相等∠D = ∠A,AAS∠DEB=∠C,BE=BC,SASASA1.下列判断中错误的有 (写序号)
①有两角和一边对应相等的两个三角形全等
②有两边和一角对应相等的两个三角形全等
③有两边和其中一边上的中线对应相等的两个三角形全等
④有一边对应相等的两个等边三角形全等
⑤有两边对应相等的两个直角三角形全等
⑥有三个角对应相等的两个三角形全等②、⑥考查知识点:全等三角形的判定方法(SSS)(SAS)(AAS)(ASA)(HL)注意点:看清文字表述2.△ABC和△A′B′C′中,下列各组条件中,不能保证:△ABC≌△A′B′C的是( )
①AB=A′B′; ② BC=B′C′; ③ AC=A′C′
④∠A =∠A′; ⑤∠B =∠B′; ⑥∠C =∠C′
具备① ② ③ B.具备① ② ④
C.具备③④ ⑤ D.具备② ③ ⑥BSSSSSAAASSAS3、如果两个三角形中两条边和其中一边上的高对应
相等,那么这两个三角形的其中有一对
角有什么关系吗?那么这两个三角形全等吗?如果两个三角形中两条边和第三边上的高对应
相等,那么这两个三角形全等吗?相等或互补4.如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,且AO平分∠BAC,则图中全等三角形共有________对。5.如图,已知:AB∥CD,AD ∥BC,OE=OF,则图中全等三角形的组数是( )
A.3 B.4 C.5 D.6解题方法:1、全等三角形的判定方法2、基本图形:平移、对称、旋转3、有规律找:一个、二个、三个4D6.如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出______个。47.用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )
SSS B.SAS C.ASA D.AASA8、得到“角平分线上的点到角两边的距离相等”
的结论,他的依据是( )
A、SSS B、HL C、SAS D、ASA9、得到“到角两边的距离相等的点在这个角的平分线上”
的结论,他的依据是( )
A、SSS B、HL C、SAS D、AASB到三角形三边距离距离相等的点,则可供选择的地址有( )
一处 B.二处 C.三处 D.四处到三角形三边距离距离相等的点是三角形 ( )
A、三条中线的交点 B、三条高线的交点
C、三条角平分线的交点 D、三边垂直平分线的交点10.如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
一处 B.二处 C.三处 D.四处D考查知识点:角平分线上的点到角两
边的距离相等注意点:1、三条公路是直线2、包括三个外角的平分线AC区别题:11.仅用一块没有刻度的直角三角板能画出一个角的平公线吗?
小刚想出了这样的办法:先将直角三角板的一个锐角顶点和∠AOB的顶点O重合,直角边l与OA重合,沿直角边2画出直线l1;再将三角板的同一锐角顶点与O重合,直角边l与OB重合,直角边2画出直线l2,l1与l2交于点P,连接OP并延长,则OP为∠AOB的平分线,你认为小刚的方法正确吗?为什么?回顾画角平分线的方法:12.如图,已知BQ是∠ABC的平分线,CQ是△ABC的外角平分线,由点Q出发,作点Q到BC、AC和AB的垂线段QM、QN和QK,垂足分别是M、N、K,则QM、QN、QK的关系是___________QM=QN=QKQM=QN的理由是QM=QK的理由是(CQ是角平分线)(BQ是角平分线)全等三角形复习(二)全等三角形画法应用已知一个三角形的两边长
分别是1cm和2cm,一个内角为400,
(1)请你借助图形画出一个满足条件的三角形;(2)你是否还能画出既满足已知条件,以现(1)不全的三角形?若能,请你在图用“尺规作图”,若不能,请说明理由.40全等三角形证明1.已知△ABC中,∠C=900,沿BE折叠这个三角形,使点C与D重合,如图,要使D恰为AB的中点,还应添加一个什么条件?(请写出三种答案)
选择(1)中的某一个添加条件作为题目的补充条件 试说明其能使D为AB中点的理由.
解: (1)添加条件:
① ② ③ .
(2)说明:∠A=300∠B=600AB=2BC注意:折叠就有全等全等三角形应用如图,一块三角形模具的阴影部
分已破损,只要从残留的模具片中度量出
哪些角,边,就可以不带残留的模具片到
店铺加工一块与原来的模具ABC的形状
和大小完全相同的模具DEF,请简要说明理由.分析:能确定一个三角形条件 的一块解:只要度量白色残留的一块中的∠B,∠C的度数和边BC的长.理由:因为两角及其夹边对应相等的两个三角形全等请欣赏答题过程2.八年级某班同学到野外上数学活动课,为测量池塘两端A,B的距离,设计如下方案.
方案一:如图1,先在平地上取一个可直接到达A,B的点C,连接AC,BC,并分别延长AC,BC至D,E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长.
方案二:
如图2,先过B作AB垂线BF,再在BF上取C,D两点,使CD=BC,接着过点D作BD的垂线DE,交AC的延长线于点E,测出DE的长即为AB的距离.
阅读后回答下列问题:
(1)方案一判定三角形全等的依据是 .
(2)方案二判定三角形全等的依据是 .
(3)方案二中作BF⊥AB,ED⊥BF的目的是 .
若仅满足∠ABD=∠BDF≠900,方案二是否成立?SASASA∠ABC=∠EDC成立请学会方案设计特别是语言描述方案一方案二全等三角形应用中的典型类问题1.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置有怎样的关系?并证明你的结论。典型在哪里?1.垂直中利用互余证角相等2.求证中的CE与DE的关系是指大小与位置关系.2.如图,已知AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD。求证:BE⊥AC证明:∵ AD为△ABC的高
∴ ∠ADB=∠ADC=90°,∠FBC+ ∠BFD=90°.
在RtΔBDF和RtΔADC中
BF=AC
DE=DC
∴ ∠BFD=∠C, ∴ ∠ FBC +∠C=90°
∴ BE⊥AC{3.如图,BD是∠ABC的角平分线,
DE⊥AB于点E,DF⊥BC于点F,
,AB=18cm,BC=12cm,
求DE的长。利用三角形面积求解全等三角形综合训练 下列说法中不正确的是 ( )
A.全等三角形的对应高相等
B.全等三角形的面积相等
C.全等三角形的周长相等
D.周长相等的两个三角形全等1、B2、已知:△ABC≌△DEF,AC∥DF,
BC∥EF.则不正确的等式是( )
A.AC=DF B.AD=BE
C.DF=EF D.BC=EFA3、下列判断中错误的是( )
A、有两角和一边对应相等的两个三角形全等
B、有两边和一角对应相等的两个三角形全等
C、有两边和其中一边上的中线对应相等的两
个三角形全等
D、有一边对应相等的两个等边三角形全等A4、如图3,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A、带①去
B、带②去
C、带③去
D、带①和②去 C12、下列说法中:
(1)如果两个三角形可以用“AAS”来判定全等,那么
一定可以用“ASA”来判定它们全等;
(2)如果两个三角形都与第三个三角形不全等,那么
这两个三角形也一定不全等;
(3)要判断两个三角形全等,给出的条件中至少要有
一边对应相等。其中正确的是( )
A、(1)和(2) B、(2)和(3)
C、(1)和(3) D、(1)(2)(3)A1.如图,D在AB上,E在
AC上,AB=AC, ∠B=∠C.
求证:AD=AE2.如图,△ABF≌△CDE,
∠B=30°, ∠BAE=∠DCF=20°,
求∠EFC的度数。3.已知:如图,点B,E,C,F在
同一直线上,AB∥DE,且
AB=DE,BE=CF.
求证:AC∥DF. 4.已知:如图12,AB=CD,
DE⊥AC,BF⊥AC,
E,F是垂足,DE=BF.
求证:(1)AF=CE
(2)AB∥CD.
利用三角形全等测距离 在一次战役中,我军阵地与敌军碉堡隔河相望。为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离。在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢?确定碉堡位置 一位战士想出来这样一个办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部.然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上.接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.1212解:在△ADB与△ADC中,有∴△ADB≌△ADC (ASA) .∴DB=DC (全等三角形对应边相等).做一做 在课后,按这个战士的方法,找出教室或操场上与你距离相等的两个点,(想一想,如何才能使得估测尽可能准确?)并通过测量加以验证.想一想例1 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,你能帮他想个办法吗? 一个叔叔帮小明出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.证明:
在△CED与△CBA中,∴DE=AB (全等三角形对应边相等).∴△CED≌△CBA(SAS)例2 如图,太阳光线AC与A’C’是平行的,同一时刻两根高度相同的直立于地上的木杆在太阳光照射下的影子一样长吗?说说理由?证明:∵AC∥A’C’,∴∠ACB=∠A’C’B’在△ABC和△A’B’C’中,有∴△ABC≌△A’B’C’(AAS). 你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗? 例3: 证明:连结DC、D’C’.在△DOC和△D’O’C’中,有∴△DOC≌△D’O’C’(SSS).∴∠DOC=∠D’O’C’ (全等三角形对应角相等).
某城市搞亮化工程,如图,在甲楼底部、乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角是相等的,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.挑战感悟与反思1、本节课你有什么收获?
2 、你有什么感受?再见
