空间向量的数量积运算(第一课时)
文档属性
| 名称 | 空间向量的数量积运算(第一课时) |  | |
| 格式 | rar | ||
| 文件大小 | 198.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-07 10:35:00 | ||
图片预览





文档简介
课件13张PPT。3.1空间向量及其运算(3)
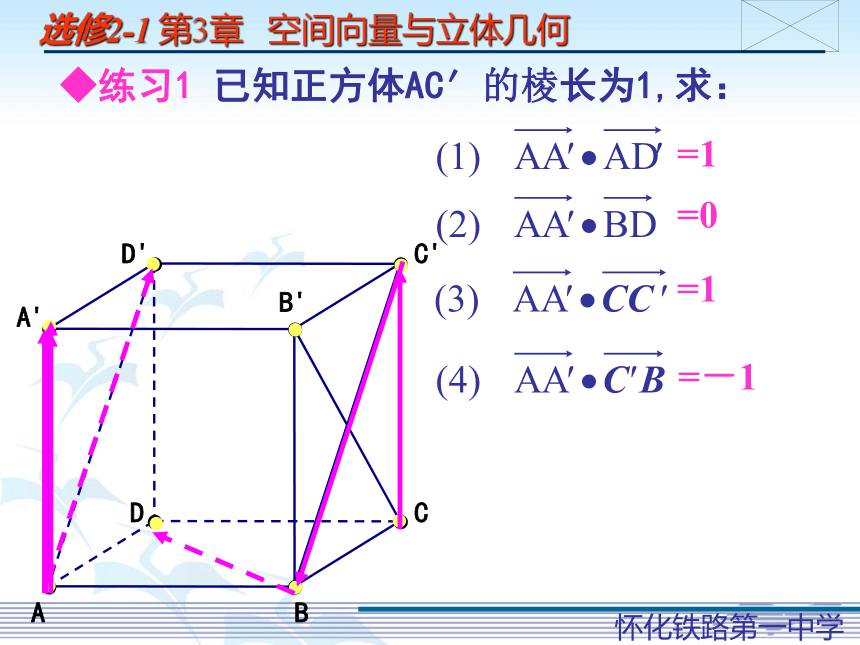
空间向量的数量积运算(一)怀化铁路第一中学 向重新1、空间两个向量的夹角AB空间两个向量的夹角的取值范围:空间向量的数量积的定义与平面向量类似[0,π]向量的垂直向量的长度(模)4 向量的数量积向量的夹角公式:5 数量积的性质(1)(2)(3)6 数量积的运算律(1)(2)(3)C'D'B'A'CDAB◆练习1 已知正方体AC′的棱长为1,求:=1=0=1=-1例1. 在平面内的一条直线,如果和这个平面的一条 斜线的射影垂直,那么它也和这条斜线垂直.已知:PO, PA分别是平面α的垂线、斜线,OA是PA在平面α内的射影,且 l ⊥OA.求证: l ⊥PA.证明:∵ l ⊥OA,取 l 的方向向量 ,∵ PO ⊥平面α,∴ PO⊥l ,即请你小结如何用向量证明空间中的线线垂直. 在平面内的一条直线,如果和这个平面的一条 斜线的射影垂直,那么它也和这条斜线垂直.这个命题的结论称为三垂线定理.PO, PA分别是α的垂线、斜线,OA是PA在平面α内的射影,三垂线定理可记为: 与射影垂直,则与斜线垂直.例1.l 是α内的一条直线.斜线垂线射影平面内的直线 在平面内的一条直线,如果和这个平面的一条 斜线的射影垂直,那么它也和这条斜线垂直. 请你写出三垂线定理的逆定理,并判断真假.三垂线定理逆定理可记为:
与斜线垂直,则与射影垂直.斜线垂线射影平面内的直线 在平面内的一条直线,如果和这个平面的一条 斜线垂直,那么它也和这条斜线的射影垂直.例2.用向量方法证明:直线和平面垂直的判定定理. 已知:m,n是平面内的两条相交直线,直线l与α的交点
为B,且 l⊥m, l⊥n .求证:l ⊥ α .证明:在α内任作一条直线g,在l, m, n, g上取非零向量 ∴ 存在唯一的实数x, y使又由已知=0.即l ⊥g.又g 是α内的任一条直线,∴ l ⊥ α .证明:◆练习2 已知空间四边形ABCD中, , ,
求证: . 由已知,∴∴课堂小结空间向量的夹角√再见!练习. 已知空间四边形OABC中, P为OA的中点, M为BC的中点, N为AC的中点, Q为OB的中点, 若AB=OC, 求证PM⊥QN.
空间向量的数量积运算(一)怀化铁路第一中学 向重新1、空间两个向量的夹角AB空间两个向量的夹角的取值范围:空间向量的数量积的定义与平面向量类似[0,π]向量的垂直向量的长度(模)4 向量的数量积向量的夹角公式:5 数量积的性质(1)(2)(3)6 数量积的运算律(1)(2)(3)C'D'B'A'CDAB◆练习1 已知正方体AC′的棱长为1,求:=1=0=1=-1例1. 在平面内的一条直线,如果和这个平面的一条 斜线的射影垂直,那么它也和这条斜线垂直.已知:PO, PA分别是平面α的垂线、斜线,OA是PA在平面α内的射影,且 l ⊥OA.求证: l ⊥PA.证明:∵ l ⊥OA,取 l 的方向向量 ,∵ PO ⊥平面α,∴ PO⊥l ,即请你小结如何用向量证明空间中的线线垂直. 在平面内的一条直线,如果和这个平面的一条 斜线的射影垂直,那么它也和这条斜线垂直.这个命题的结论称为三垂线定理.PO, PA分别是α的垂线、斜线,OA是PA在平面α内的射影,三垂线定理可记为: 与射影垂直,则与斜线垂直.例1.l 是α内的一条直线.斜线垂线射影平面内的直线 在平面内的一条直线,如果和这个平面的一条 斜线的射影垂直,那么它也和这条斜线垂直. 请你写出三垂线定理的逆定理,并判断真假.三垂线定理逆定理可记为:
与斜线垂直,则与射影垂直.斜线垂线射影平面内的直线 在平面内的一条直线,如果和这个平面的一条 斜线垂直,那么它也和这条斜线的射影垂直.例2.用向量方法证明:直线和平面垂直的判定定理. 已知:m,n是平面内的两条相交直线,直线l与α的交点
为B,且 l⊥m, l⊥n .求证:l ⊥ α .证明:在α内任作一条直线g,在l, m, n, g上取非零向量 ∴ 存在唯一的实数x, y使又由已知=0.即l ⊥g.又g 是α内的任一条直线,∴ l ⊥ α .证明:◆练习2 已知空间四边形ABCD中, , ,
求证: . 由已知,∴∴课堂小结空间向量的夹角√再见!练习. 已知空间四边形OABC中, P为OA的中点, M为BC的中点, N为AC的中点, Q为OB的中点, 若AB=OC, 求证PM⊥QN.
