6.1 平行四边形的性质 培优练习(含答案)
文档属性
| 名称 | 6.1 平行四边形的性质 培优练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 11:32:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.1平行四边形的性质培优练习北师大版2024—2025学年八年级下册
一、选择题
1.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD,交BC于点E,且∠ADC=60°,ABBC,连接OE,下列结论①∠CAD=30°;②OE⊥AC;③BDAB;④S四边形ABOES△OCD;其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图,平行四边形ABCD的周长为20cm,AB≠AD,AC、BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
A.8cm B.10cm C.12cm D.20cm
3.如图,点E是平行四边形ABCD的CD边上一动点,以BE为一条边作平行四边形BEFG,使点A始终在GF边上,在动点E从点C向点D的运动过程中,关于平行四边形BEFG的面积,下列说法正确的是( )
A.始终不变 B.逐渐减小
C.先减小再增大 D.不能确定
4.如图,在平行四边形ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则CD+AE的值等于( )
A.6 B.8 C.10 D.14
5.如图,在 ABCD中,AB=3,∠ABC与∠BCD的角平分线交于点E,若点E恰好在AD边上,则CE2+BE2的值为( )
A.12 B.16 C.24 D.36
6.如图,在平行四边形ABCD中,E为边BC延长线上一点,连接AE,DE.若平行四边形ABCD的面积为12,则△ADE的面积为( )
A.3 B.4 C.6 D.8
二、填空题
7.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 .
8.如图,在平行四边形ABCD中,AB=5,AD=4,∠B=60°,点E,F分别为AB,BC边上的一点,连接EF.点B关于EF的对称点P恰好落在CD上.当BE最小时,求PF的长为 .
9.如图,在Rt△ABC中,∠B=90°,BC=4,AB=3,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是 .
10.已知平行四边形ABCD中,∠A=30°,,BD=2,则平行四边形的面积为 .
11.如图,在平行四边形ABCD中,对角线AC、BD相交于O点,AC=AB,E是AB边的中点,G、F为BC上的点,连接OG和EF,若AB=26,BC=20,GF=10,则图中阴影部分的面积为 .
12.如图,平行四边形ABCD中,AE⊥BC于点E,BE=2,EC=1,∠BAE=∠AEF=∠ADF,则DF的长为 .
13.如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=6,则GE= .
三、解答题
14.如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.
15.如图,在 ABCD中,点E为BC上一点,连接AE并延长交DC的延长线于点F,AD=DF,连接DE.
(1)求证:AE平分∠BAD;
(2)若点E为BC中点,求证:DE⊥AF;
(3)若AE=13,DE=15,AD=14,求 ABCD的面积.
16.如图,在 ABCD中,∠B=60°,AE平分∠BAD交BC于点E,EF⊥AE交CD于点F.
(1)求证:CE=CF;
(2)M为BA延长线上一点,且AM=CF.若AD=5,FD=3,求MF的长.
17.如图,在平行四边形ABCD中,BE、DF分别平分∠ABC、∠ADC,交AC分别于点E、F.已知平行四边形ABCD的周长为48.
(1)求证:BE=DF;
(2)过点E作EM⊥AB于点M,若EM=6,求△ACD的面积.
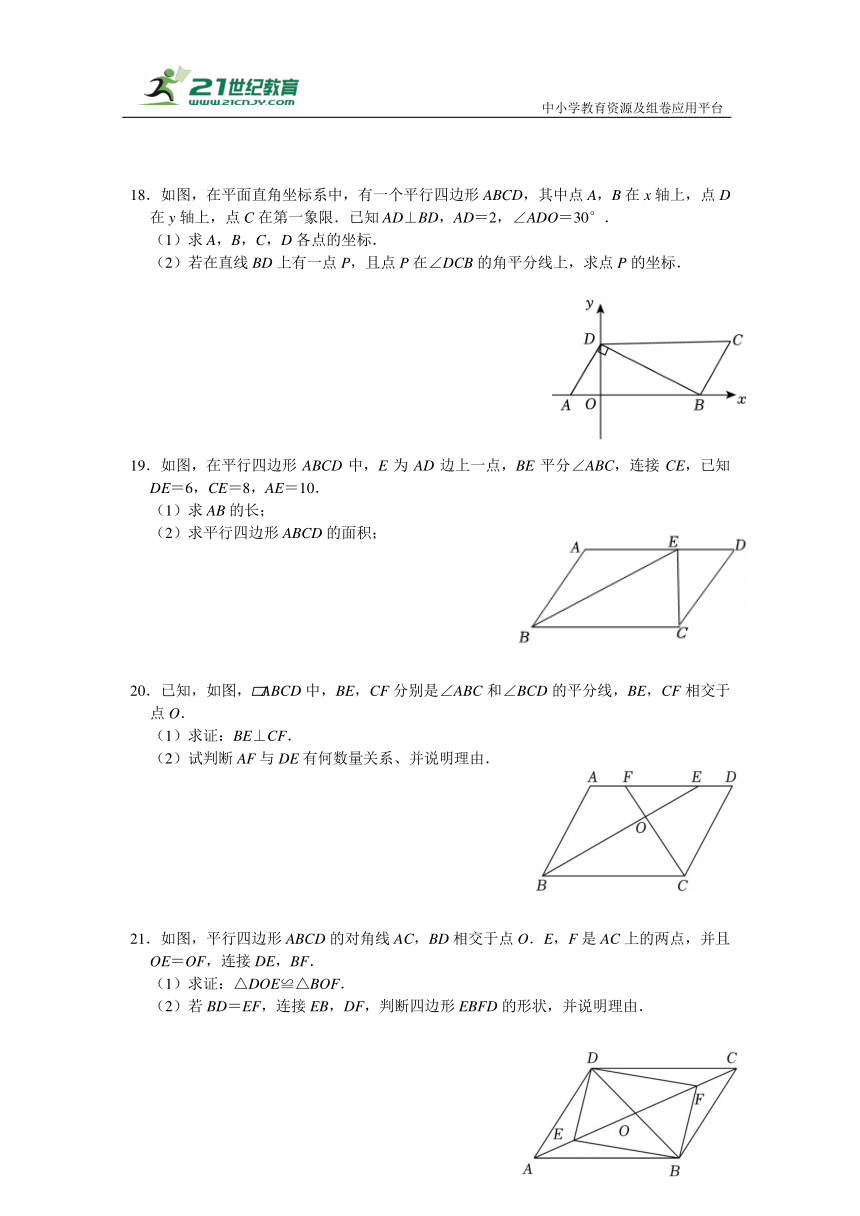
18.如图,在平面直角坐标系中,有一个平行四边形ABCD,其中点A,B在x轴上,点D在y轴上,点C在第一象限.已知AD⊥BD,AD=2,∠ADO=30°.
(1)求A,B,C,D各点的坐标.
(2)若在直线BD上有一点P,且点P在∠DCB的角平分线上,求点P的坐标.
19.如图,在平行四边形ABCD中,E为AD边上一点,BE平分∠ABC,连接CE,已知DE=6,CE=8,AE=10.
(1)求AB的长;
(2)求平行四边形ABCD的面积;
20.已知,如图, ABCD中,BE,CF分别是∠ABC和∠BCD的平分线,BE,CF相交于点O.
(1)求证:BE⊥CF.
(2)试判断AF与DE有何数量关系、并说明理由.
21.如图,平行四边形ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且OE=OF,连接DE,BF.
(1)求证:△DOE≌△BOF.
(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6
答案 D B A B D C
二、填空题
7.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 36° .
【解答】解:如图:
,
∵四边形ABCD为平行四边形,有两个内角的度数比为1:4,
∴AD∥BC,∠A=4∠B,
∴∠A+∠B=180°,
∴4∠B+∠B=180°,
∴∠B=36°,
∴∠A=144°,
∴平行四边形ABCD中较小内角的度数为36°,
故答案为:36°.
8.如图,在平行四边形ABCD中,AB=5,AD=4,∠B=60°,点E,F分别为AB,BC边上的一点,连接EF.点B关于EF的对称点P恰好落在CD上.当BE最小时,求PF的长为 6﹣2 .
9.如图,在Rt△ABC中,∠B=90°,BC=4,AB=3,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是 3 .
【解答】解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC,
∴当OD取最小值时,DE线段最短,此时OD⊥BC,
∴OD是△ABC的中位线,
∴,
∴ED=2OD=3,
故答案为:3.
10.已知平行四边形ABCD中,∠A=30°,,BD=2,则平行四边形的面积为 2或4 .
【解答】解:过D作DE⊥AB于E,
在Rt△ADE中,∵∠A=30°,AD=2,
∴DEAD,AEAD=3,
在Rt△BDE中,
∵BD=2,
∴BE2,
如图1,∴AB=4,
∴平行四边形ABCD的面积=AB DE=4;
如图2,AB=2,
∴平行四边形ABCD的面积=AB DE=2.
故答案为:2或4.
11.【解答】解:如图所示,连接EO,EG,OF,
∵平行四边形ABCD中,对角线AC、BD相交于O点,
∴O是AC边的中点,
又∵E是AB边的中点,
∴EO是△ABC的中位线,
∴EO∥BG,.
又∵GF=10,
∴EO=GF,
∴四边形EOFG是平行四边形.
∴,
又∵EO∥BG,
∴S△EOG=S△EOB,
∴S△EOP+=S△FGP=S△EOB.
∴S阴影部分=S△AOE+S△EOP+S△FGP=S△AOE+S△EOB=S△ABO.
∵AC=AB=26,BC=20,
∴等腰△ABC中BC边上的高为,
∴.
∵O是AC边的中点,
∴.
∴阴影部分的面积为120.
故答案为:120.
12.【解答】解:设∠BAE=∠AEF=∠ADF=α,则∠BFE=2α,
∵AE⊥BC,则∠AEB=90°,
∴∠B=∠BEF=90°﹣α,则BF=EF,
又∵∠BAE=∠AEF,
∴AF=EF,则F为AB的中点,
延长DA,EF交于点G,
∵四边形ABCD是平行四边形,BE=2,EC=1,
∴AD=BC=BE+EC=3,AD∥BC,
∴∠G=∠BEF,∠FAG=∠FBE,∠AEB=∠DAE=90°,
∴△AFG≌△BFE(AAS),
∴∠FAG=∠B=90°﹣α,GF=EF,AG=BE=2,则DG=AD+AG=5,
则∠AFD=∠FAG﹣∠ADF=90°﹣α﹣α=90°﹣2α,
∴∠DFE=180°﹣∠AFD﹣∠BFE=180°﹣(90°﹣2α)﹣2α=90°,
即:DF⊥GE,
又∵GF=EF,
∴DF垂直平分GE,
∴DE=DG=5,
在Rt△AED中,由勾股定理可得:,
取AG的中点H,连接FH,则,DH=AH+AD=4,
∵GF=EF,则F为EG的中点,
∴FH为△AEG的中位线,
∴,FH∥AE,
∴∠FHD=∠DAE=90°,
在Rt△DFH中,由勾股定理可得:,
故答案为:.
13.【解答】解:取BE的中点H,连接FH、CH,如图:
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,FHAB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E是CD的中点,
∴ECCD,
∴FH∥EC,FH=EC,
∴四边形FHCE是平行四边形,
∴GE=GHEH.
∵BE=6,H是BE的中点,
∴EH=3,
∴GE.
故答案为:.
14.如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.
【分析】(1)利用平行四边形的性质得出∠5=∠3,∠AEB=∠4,进而利用全等三角形
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠5=∠3,
∵∠1=∠2,
∴∠AEB=∠4,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)由(1)得△ABE≌△CDF,
∴AE=CF,
∵∠1=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
15.如图,在 ABCD中,点E为BC上一点,连接AE并延长交DC的延长线于点F,AD=DF,连接DE.
(1)求证:AE平分∠BAD;
(2)若点E为BC中点,求证:DE⊥AF;
(3)若AE=13,DE=15,AD=14,求 ABCD的面积.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAE=∠AFD,
∵AD=DF,
∴∠DAE=∠AFD,
∴∠BAE=∠DAE,
∴AE平分∠BAD;
(2)证明:∵点E为BC中点,
∴BE=EC,
∵∠BAE=∠AFD,∠AEB=∠FEC,
∴△ABE≌△FCE(AAS),
∴AE=EF,
∵AD=DF,
∴DE⊥AF;
(3)解:如图,过点E作EM⊥AD于M,设AM=x,则DM=14﹣x.
根据勾股定理得132﹣x2=152﹣(14﹣x)2,
解得x=5,
∴,
∴S ABCD=EM AD=168.
16.如图,在 ABCD中,∠B=60°,AE平分∠BAD交BC于点E,EF⊥AE交CD于点F.
(1)求证:CE=CF;
(2)M为BA延长线上一点,且AM=CF.若AD=5,FD=3,求MF的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,∠DAB=∠C=180°﹣∠B=120°,
∵AE平分∠BAD,
∴∠BAE∠BAD=60°,
∴△ABE是等边三角形,
∴BE=AB,∠AEB=60°,
∵AE⊥EF,
∴∠FEC=30°,
∴∠CFE=180°﹣∠C﹣∠CEF=30°=∠CEF,
∴CE=CF;
(2)解:连接AC,过A作AH⊥BC于H,
设CE=CF=x,则BE=AB=CD=x+3,AD=BC=2x+3=5,
解得:x=1,
∴CE=1,AB=4,
∵∠B=60°,AH⊥BC,
∴∠BAH=30°,
∴BHAB=2,
∴HC=BC﹣BH=3,
∵AH⊥BC,
∴AC2﹣HC2=AB2﹣BH2,
∴AC2﹣32=42﹣22,
∴AC,
∵AM=CF,AM∥CF,
∴四边形AMFC是平行四边形,
∴MF=AC.
17.如图,在平行四边形ABCD中,BE、DF分别平分∠ABC、∠ADC,交AC分别于点E、F.已知平行四边形ABCD的周长为48.
(1)求证:BE=DF;
(2)过点E作EM⊥AB于点M,若EM=6,求△ACD的面积.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC,
∴∠DAC=∠BCA,
∵BE、DF分别平分∠ABC、∠ADC,
∴∠ADF∠ADC,∠CBE∠ABC,
∴∠ADF=∠CBE,
又∵AD=BC,
∴△ADF≌△CBE(ASA),
∴BE=DF;
(2)解:如图,过点E作EN⊥BC于N,
∵BE平分∠ABC,EM⊥AB,EN⊥BC,
∴EM=EN=6,
∵平行四边形ABCD的周长为48,
∴AB+BC=24,
∴S△ABC=S△ACD=S△ABE+S△BCEAB EMBC EN6×24=72.
18.如图,在平面直角坐标系中,有一个平行四边形ABCD,其中点A,B在x轴上,点D在y轴上,点C在第一象限.已知AD⊥BD,AD=2,∠ADO=30°.
(1)求A,B,C,D各点的坐标.
(2)若在直线BD上有一点P,且点P在∠DCB的角平分线上,求点P的坐标.
【解答】解:(1)∵四边形ABCD是平行四边形,点A,B在x轴上,点D在y轴上,
∴CD∥x轴,∠AOD=∠BOD=90°,
∵AD⊥BD,AD=2,∠ADO=30°,
∴∠ADB=90°,OAAD=1,
∴∠DBO=90°﹣∠BDO=∠ADO=30°,OD,
∴A(﹣1,0),D(0,),点C的纵坐标为,
∵BD=2OD,
∴OBOD3,
∴B(3,0),CD=AB=OA+OB=1+3=4,
∴C(4,),
∴A(﹣1,0),B(3,0),C(4,),D(0,).
(2)如图,作PF⊥x轴于点F,交CD于点E,则∠PED=∠PFB=90°,
∴PE⊥CD,
∵∠DCB=∠DAB=90°﹣∠ADO=60°,点P在∠DCB的角平分线上,
∴∠PCD=∠PCB∠DCB=30°,
∵∠PDC=∠DBO=30°,
∴∠PCD=∠PDC,
∴PD=PC,
∴OF=DE=CECD=2,
∴BF=OB﹣OF=3﹣2=1,点P的横坐标为2,
∵PB=2PF,
∴BFPF=1,
∴PF,
∴P(2,).
19.如图,在平行四边形ABCD中,E为AD边上一点,BE平分∠ABC,连接CE,已知DE=6,CE=8,AE=10.
(1)求AB的长;
(2)求平行四边形ABCD的面积;
【解答】解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠AEB,
∴AB=AE=10,
(2)∵四边形ABCD是平行四边形.
∴CD=AB=10,
在△CED中,CD=10,DE=6,CE=8,
∴ED2+CE2=CD2,
∴∠CED=90°.
∴CE⊥AD,
∴平行四边形ABCD的面积=AD CE=(10+6)×8=128.
20.已知,如图, ABCD中,BE,CF分别是∠ABC和∠BCD的平分线,BE,CF相交于点O.
(1)求证:BE⊥CF.
(2)试判断AF与DE有何数量关系、并说明理由.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠ABC+∠BCD=180°,
又∵BE,CF分别是∠ABC和∠BCD的平分线,
∴∠OBC+∠OCB,
∴∠BOC=90°,
∴BE⊥CF.
(2)解:AF=DE,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠EBC,
又∵BE平分∠ABC,
∴∠ABE=∠EBC=∠AEB,
∴AB=AE,
同理可得CD=DF,
又∵AB=CD,
∴AE=DF,
∴AF=DE.
21.如图,平行四边形ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且OE=OF,连接DE,BF.
(1)求证:△DOE≌△BOF.
(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(SAS).
(2)解:四边形EBFD是矩形,理由如下:
∵OB=OD,OE=OF,
∴四边形EBFD是平行四边形.
∵BD=EF,
∴四边形EBFD是矩形.
6.1平行四边形的性质培优练习北师大版2024—2025学年八年级下册
一、选择题
1.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD,交BC于点E,且∠ADC=60°,ABBC,连接OE,下列结论①∠CAD=30°;②OE⊥AC;③BDAB;④S四边形ABOES△OCD;其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图,平行四边形ABCD的周长为20cm,AB≠AD,AC、BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
A.8cm B.10cm C.12cm D.20cm
3.如图,点E是平行四边形ABCD的CD边上一动点,以BE为一条边作平行四边形BEFG,使点A始终在GF边上,在动点E从点C向点D的运动过程中,关于平行四边形BEFG的面积,下列说法正确的是( )
A.始终不变 B.逐渐减小
C.先减小再增大 D.不能确定
4.如图,在平行四边形ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则CD+AE的值等于( )
A.6 B.8 C.10 D.14
5.如图,在 ABCD中,AB=3,∠ABC与∠BCD的角平分线交于点E,若点E恰好在AD边上,则CE2+BE2的值为( )
A.12 B.16 C.24 D.36
6.如图,在平行四边形ABCD中,E为边BC延长线上一点,连接AE,DE.若平行四边形ABCD的面积为12,则△ADE的面积为( )
A.3 B.4 C.6 D.8
二、填空题
7.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 .
8.如图,在平行四边形ABCD中,AB=5,AD=4,∠B=60°,点E,F分别为AB,BC边上的一点,连接EF.点B关于EF的对称点P恰好落在CD上.当BE最小时,求PF的长为 .
9.如图,在Rt△ABC中,∠B=90°,BC=4,AB=3,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是 .
10.已知平行四边形ABCD中,∠A=30°,,BD=2,则平行四边形的面积为 .
11.如图,在平行四边形ABCD中,对角线AC、BD相交于O点,AC=AB,E是AB边的中点,G、F为BC上的点,连接OG和EF,若AB=26,BC=20,GF=10,则图中阴影部分的面积为 .
12.如图,平行四边形ABCD中,AE⊥BC于点E,BE=2,EC=1,∠BAE=∠AEF=∠ADF,则DF的长为 .
13.如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=6,则GE= .
三、解答题
14.如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.
15.如图,在 ABCD中,点E为BC上一点,连接AE并延长交DC的延长线于点F,AD=DF,连接DE.
(1)求证:AE平分∠BAD;
(2)若点E为BC中点,求证:DE⊥AF;
(3)若AE=13,DE=15,AD=14,求 ABCD的面积.
16.如图,在 ABCD中,∠B=60°,AE平分∠BAD交BC于点E,EF⊥AE交CD于点F.
(1)求证:CE=CF;
(2)M为BA延长线上一点,且AM=CF.若AD=5,FD=3,求MF的长.
17.如图,在平行四边形ABCD中,BE、DF分别平分∠ABC、∠ADC,交AC分别于点E、F.已知平行四边形ABCD的周长为48.
(1)求证:BE=DF;
(2)过点E作EM⊥AB于点M,若EM=6,求△ACD的面积.
18.如图,在平面直角坐标系中,有一个平行四边形ABCD,其中点A,B在x轴上,点D在y轴上,点C在第一象限.已知AD⊥BD,AD=2,∠ADO=30°.
(1)求A,B,C,D各点的坐标.
(2)若在直线BD上有一点P,且点P在∠DCB的角平分线上,求点P的坐标.
19.如图,在平行四边形ABCD中,E为AD边上一点,BE平分∠ABC,连接CE,已知DE=6,CE=8,AE=10.
(1)求AB的长;
(2)求平行四边形ABCD的面积;
20.已知,如图, ABCD中,BE,CF分别是∠ABC和∠BCD的平分线,BE,CF相交于点O.
(1)求证:BE⊥CF.
(2)试判断AF与DE有何数量关系、并说明理由.
21.如图,平行四边形ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且OE=OF,连接DE,BF.
(1)求证:△DOE≌△BOF.
(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6
答案 D B A B D C
二、填空题
7.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 36° .
【解答】解:如图:
,
∵四边形ABCD为平行四边形,有两个内角的度数比为1:4,
∴AD∥BC,∠A=4∠B,
∴∠A+∠B=180°,
∴4∠B+∠B=180°,
∴∠B=36°,
∴∠A=144°,
∴平行四边形ABCD中较小内角的度数为36°,
故答案为:36°.
8.如图,在平行四边形ABCD中,AB=5,AD=4,∠B=60°,点E,F分别为AB,BC边上的一点,连接EF.点B关于EF的对称点P恰好落在CD上.当BE最小时,求PF的长为 6﹣2 .
9.如图,在Rt△ABC中,∠B=90°,BC=4,AB=3,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是 3 .
【解答】解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC,
∴当OD取最小值时,DE线段最短,此时OD⊥BC,
∴OD是△ABC的中位线,
∴,
∴ED=2OD=3,
故答案为:3.
10.已知平行四边形ABCD中,∠A=30°,,BD=2,则平行四边形的面积为 2或4 .
【解答】解:过D作DE⊥AB于E,
在Rt△ADE中,∵∠A=30°,AD=2,
∴DEAD,AEAD=3,
在Rt△BDE中,
∵BD=2,
∴BE2,
如图1,∴AB=4,
∴平行四边形ABCD的面积=AB DE=4;
如图2,AB=2,
∴平行四边形ABCD的面积=AB DE=2.
故答案为:2或4.
11.【解答】解:如图所示,连接EO,EG,OF,
∵平行四边形ABCD中,对角线AC、BD相交于O点,
∴O是AC边的中点,
又∵E是AB边的中点,
∴EO是△ABC的中位线,
∴EO∥BG,.
又∵GF=10,
∴EO=GF,
∴四边形EOFG是平行四边形.
∴,
又∵EO∥BG,
∴S△EOG=S△EOB,
∴S△EOP+=S△FGP=S△EOB.
∴S阴影部分=S△AOE+S△EOP+S△FGP=S△AOE+S△EOB=S△ABO.
∵AC=AB=26,BC=20,
∴等腰△ABC中BC边上的高为,
∴.
∵O是AC边的中点,
∴.
∴阴影部分的面积为120.
故答案为:120.
12.【解答】解:设∠BAE=∠AEF=∠ADF=α,则∠BFE=2α,
∵AE⊥BC,则∠AEB=90°,
∴∠B=∠BEF=90°﹣α,则BF=EF,
又∵∠BAE=∠AEF,
∴AF=EF,则F为AB的中点,
延长DA,EF交于点G,
∵四边形ABCD是平行四边形,BE=2,EC=1,
∴AD=BC=BE+EC=3,AD∥BC,
∴∠G=∠BEF,∠FAG=∠FBE,∠AEB=∠DAE=90°,
∴△AFG≌△BFE(AAS),
∴∠FAG=∠B=90°﹣α,GF=EF,AG=BE=2,则DG=AD+AG=5,
则∠AFD=∠FAG﹣∠ADF=90°﹣α﹣α=90°﹣2α,
∴∠DFE=180°﹣∠AFD﹣∠BFE=180°﹣(90°﹣2α)﹣2α=90°,
即:DF⊥GE,
又∵GF=EF,
∴DF垂直平分GE,
∴DE=DG=5,
在Rt△AED中,由勾股定理可得:,
取AG的中点H,连接FH,则,DH=AH+AD=4,
∵GF=EF,则F为EG的中点,
∴FH为△AEG的中位线,
∴,FH∥AE,
∴∠FHD=∠DAE=90°,
在Rt△DFH中,由勾股定理可得:,
故答案为:.
13.【解答】解:取BE的中点H,连接FH、CH,如图:
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,FHAB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E是CD的中点,
∴ECCD,
∴FH∥EC,FH=EC,
∴四边形FHCE是平行四边形,
∴GE=GHEH.
∵BE=6,H是BE的中点,
∴EH=3,
∴GE.
故答案为:.
14.如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.
【分析】(1)利用平行四边形的性质得出∠5=∠3,∠AEB=∠4,进而利用全等三角形
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠5=∠3,
∵∠1=∠2,
∴∠AEB=∠4,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)由(1)得△ABE≌△CDF,
∴AE=CF,
∵∠1=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
15.如图,在 ABCD中,点E为BC上一点,连接AE并延长交DC的延长线于点F,AD=DF,连接DE.
(1)求证:AE平分∠BAD;
(2)若点E为BC中点,求证:DE⊥AF;
(3)若AE=13,DE=15,AD=14,求 ABCD的面积.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAE=∠AFD,
∵AD=DF,
∴∠DAE=∠AFD,
∴∠BAE=∠DAE,
∴AE平分∠BAD;
(2)证明:∵点E为BC中点,
∴BE=EC,
∵∠BAE=∠AFD,∠AEB=∠FEC,
∴△ABE≌△FCE(AAS),
∴AE=EF,
∵AD=DF,
∴DE⊥AF;
(3)解:如图,过点E作EM⊥AD于M,设AM=x,则DM=14﹣x.
根据勾股定理得132﹣x2=152﹣(14﹣x)2,
解得x=5,
∴,
∴S ABCD=EM AD=168.
16.如图,在 ABCD中,∠B=60°,AE平分∠BAD交BC于点E,EF⊥AE交CD于点F.
(1)求证:CE=CF;
(2)M为BA延长线上一点,且AM=CF.若AD=5,FD=3,求MF的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,∠DAB=∠C=180°﹣∠B=120°,
∵AE平分∠BAD,
∴∠BAE∠BAD=60°,
∴△ABE是等边三角形,
∴BE=AB,∠AEB=60°,
∵AE⊥EF,
∴∠FEC=30°,
∴∠CFE=180°﹣∠C﹣∠CEF=30°=∠CEF,
∴CE=CF;
(2)解:连接AC,过A作AH⊥BC于H,
设CE=CF=x,则BE=AB=CD=x+3,AD=BC=2x+3=5,
解得:x=1,
∴CE=1,AB=4,
∵∠B=60°,AH⊥BC,
∴∠BAH=30°,
∴BHAB=2,
∴HC=BC﹣BH=3,
∵AH⊥BC,
∴AC2﹣HC2=AB2﹣BH2,
∴AC2﹣32=42﹣22,
∴AC,
∵AM=CF,AM∥CF,
∴四边形AMFC是平行四边形,
∴MF=AC.
17.如图,在平行四边形ABCD中,BE、DF分别平分∠ABC、∠ADC,交AC分别于点E、F.已知平行四边形ABCD的周长为48.
(1)求证:BE=DF;
(2)过点E作EM⊥AB于点M,若EM=6,求△ACD的面积.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC,
∴∠DAC=∠BCA,
∵BE、DF分别平分∠ABC、∠ADC,
∴∠ADF∠ADC,∠CBE∠ABC,
∴∠ADF=∠CBE,
又∵AD=BC,
∴△ADF≌△CBE(ASA),
∴BE=DF;
(2)解:如图,过点E作EN⊥BC于N,
∵BE平分∠ABC,EM⊥AB,EN⊥BC,
∴EM=EN=6,
∵平行四边形ABCD的周长为48,
∴AB+BC=24,
∴S△ABC=S△ACD=S△ABE+S△BCEAB EMBC EN6×24=72.
18.如图,在平面直角坐标系中,有一个平行四边形ABCD,其中点A,B在x轴上,点D在y轴上,点C在第一象限.已知AD⊥BD,AD=2,∠ADO=30°.
(1)求A,B,C,D各点的坐标.
(2)若在直线BD上有一点P,且点P在∠DCB的角平分线上,求点P的坐标.
【解答】解:(1)∵四边形ABCD是平行四边形,点A,B在x轴上,点D在y轴上,
∴CD∥x轴,∠AOD=∠BOD=90°,
∵AD⊥BD,AD=2,∠ADO=30°,
∴∠ADB=90°,OAAD=1,
∴∠DBO=90°﹣∠BDO=∠ADO=30°,OD,
∴A(﹣1,0),D(0,),点C的纵坐标为,
∵BD=2OD,
∴OBOD3,
∴B(3,0),CD=AB=OA+OB=1+3=4,
∴C(4,),
∴A(﹣1,0),B(3,0),C(4,),D(0,).
(2)如图,作PF⊥x轴于点F,交CD于点E,则∠PED=∠PFB=90°,
∴PE⊥CD,
∵∠DCB=∠DAB=90°﹣∠ADO=60°,点P在∠DCB的角平分线上,
∴∠PCD=∠PCB∠DCB=30°,
∵∠PDC=∠DBO=30°,
∴∠PCD=∠PDC,
∴PD=PC,
∴OF=DE=CECD=2,
∴BF=OB﹣OF=3﹣2=1,点P的横坐标为2,
∵PB=2PF,
∴BFPF=1,
∴PF,
∴P(2,).
19.如图,在平行四边形ABCD中,E为AD边上一点,BE平分∠ABC,连接CE,已知DE=6,CE=8,AE=10.
(1)求AB的长;
(2)求平行四边形ABCD的面积;
【解答】解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠AEB,
∴AB=AE=10,
(2)∵四边形ABCD是平行四边形.
∴CD=AB=10,
在△CED中,CD=10,DE=6,CE=8,
∴ED2+CE2=CD2,
∴∠CED=90°.
∴CE⊥AD,
∴平行四边形ABCD的面积=AD CE=(10+6)×8=128.
20.已知,如图, ABCD中,BE,CF分别是∠ABC和∠BCD的平分线,BE,CF相交于点O.
(1)求证:BE⊥CF.
(2)试判断AF与DE有何数量关系、并说明理由.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠ABC+∠BCD=180°,
又∵BE,CF分别是∠ABC和∠BCD的平分线,
∴∠OBC+∠OCB,
∴∠BOC=90°,
∴BE⊥CF.
(2)解:AF=DE,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠EBC,
又∵BE平分∠ABC,
∴∠ABE=∠EBC=∠AEB,
∴AB=AE,
同理可得CD=DF,
又∵AB=CD,
∴AE=DF,
∴AF=DE.
21.如图,平行四边形ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且OE=OF,连接DE,BF.
(1)求证:△DOE≌△BOF.
(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(SAS).
(2)解:四边形EBFD是矩形,理由如下:
∵OB=OD,OE=OF,
∴四边形EBFD是平行四边形.
∵BD=EF,
∴四边形EBFD是矩形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
